SS系列机车制动工况及轮对椭圆化在线监测的研究与实现

严 俊

(湖南铁道职业技术学院,湖南株洲,412001)

0 引言

对于铁路运输来讲，列车的运行过程中，制动系统起着保证运输安全的重要作用。目前我国SS系列机车的制动装置采用独立箱式单元制动器，它是以制动器箱体为基础，将制动缸、制动传动装置和闸瓦间隙调整装置安装于箱体内部，闸瓦装置安装于箱体外侧的一种基础制动装置，当制动缸充气时，活塞带动活塞杆移动，使闸瓦压在车轮踏面上机械摩擦产生制动力实现制动作用；当制动缸排气时，活塞杆在缓解弹簧的推动下，使闸瓦离开车轮踏面而缓解。闸瓦是采用铸铁或其他材料制成，频繁制动，闸瓦磨损严重，需要及时更换，否则会出现制动失灵的事故；制动器的传动装置缓解采用弹簧推动，弹簧经常使用会发生机械疲劳，造成不能缓解到位，致使闸瓦与车轮踏面粘合，处于长时间制动状态，如不能及时发现处理，会使车轮温度上升，会造成轮箍迟缓，导致翻车事故；轮对椭圆化，车辆系统运行品质严重恶化，其横向稳定性和轮重减载率大大降低，从而减小车辆/轨道系统各部件使用寿命、增大脱轨风险。

针对这些情况，设计了一种机车制动工况及轮对椭圆化在线监测系统，解决了监测制动单元制动、缓解是否正常，闸瓦磨损情况，轮箍磨损情况及椭圆化情况，对确保机车运行安全具有重要意义。

1 系统设计

系统采用了两个位移传感器及安装位置来检测各参数，将传感器机械变化产生的信号、列车速度及制动信号传送到中央处理单元来计算闸瓦的厚度，轮对踏面的磨损程度，轮对椭圆化程度，制动器的缓解到位程度。如果数据超过了设定的参数，将驱动声光报警，提示操作人员。图1所示为原理框图。

图1 在线监测原理框图

本研究采用工控机作为中央处理部件，专用A/D模块，拉杆移动式电阻位移传感器，传感器的输出信号为4～20mA的电流信号，该信号传送距离远，不会受机车运行的干扰。

在人机界面上可根据安装情况来设定传感器的初始位移，作为制动器缓解到位的初始点，在初始位置时（闸瓦无磨损、制动器缓解到位、轮对踏面无磨损）闸瓦与轮对轮箍踏面的间隙为δ。如果出现缓解控制后，缓解复位出现位移偏差，如该位移偏差过大（操作人员可根据行程要求自行设定），工控机发出声光报警提示驾驶员或检修人员，缓解不到位，应处理故障。

2 制动工况检测的实现

2.1 闸瓦与轮对轮箍踏面间隙的检测及计算

位移传感器1的“固定外壳”固定在制动单元的箱体上，位移传感器的检测头固定在闸瓦托杆与闸瓦托的连接轴上，当制动器制动时，带动闸瓦托移动，传感器1的检测头随之移动。在初始情况下（闸瓦无磨损、制动器缓解到位、轮对踏面无磨损）传感器1的固定端到检测头的固定端的长度为X10，在闸瓦磨损、轮对踏面磨损、制动器缓解到位的情况下，传感器1的固定端到检测头的固定端的长度为X1，制动器缓解复位后再次制动的起始位置发生变化，变化量为ΔX10，如图2所示。用公式（1）可求得：

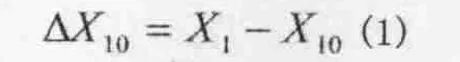
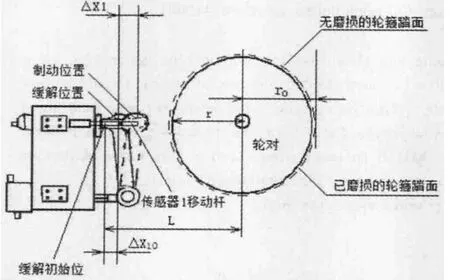
图2 闸瓦与轮对轮箍踏面间隙检测及计算参数示意图

工控机将列车速度和制动信号读出，当制动器进行制动时，列车的速度下降，此时，表示列车产生制动，将对应传感器1的固定端到检测头的固定端的长度X2记录，用公式（2）可得闸瓦与轮对踏面的间隙ΔX1。

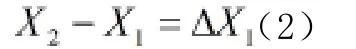
2.2 轮对轮箍踏面磨损及轮对椭圆化检测及计算

位移传感器2的“固定外壳” 固定在闸瓦托杆与闸瓦托的连接轴上，位移传感器2的检测头为自恢复的，即没有机械碰撞时，为初始位，固定端到检测头的长度为最长，有机械碰撞时，移动杆回缩，产生位移，如图3所示。

位移传感器2的检测头在无机械碰撞的情况下，固定端到检测头的长度为X2。当制动器缓解时，位移传感器2的移动杆不与机车轮对踏面（没有磨损过的尺寸）接触，预留1mm的间隙（间隙可通过固定外壳的安装改变）。r0为轮对无磨损的半径，r为轮对磨损后的半径，Δr为磨损尺寸；L为缓解初始位置到轮对圆心的长度。当制动器进行制动时，检测头向轮对方向移动被轮对踏面挤压，检测头回缩，产生位移ΔX2。轮对轮箍踏面磨损的尺寸为Δr可用以下方程推导得出。

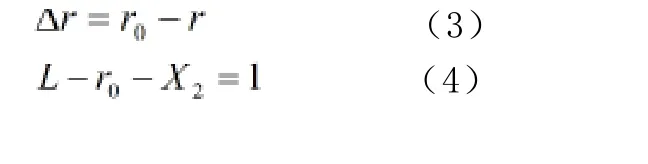
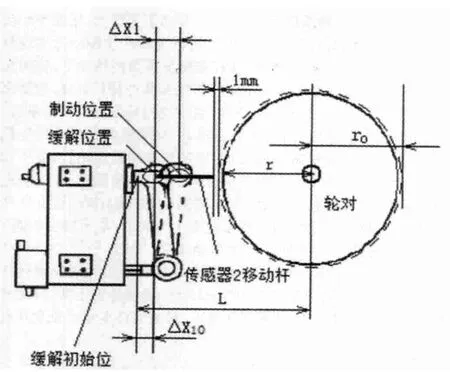
图3 轮对轮箍踏面磨损检测及计算参数示意图

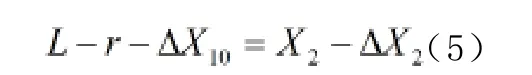
通过以上公式可推导出：

该结果即是轮对踏面的磨损尺寸，通过人机界面将磨损尺寸大小显示出来，驾驶员或检修人员可知道，轮对的磨损情况，以便及时处理。

如果轮对发生了椭圆化情况，Δr将是一个随时间变化的函数Δr（t），即：

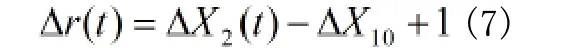
2.3 闸瓦磨损的检测及计算

闸瓦磨损可通过相应的检测数据计算出来，各数据见图4所示，图中L1为闸瓦托杆与闸瓦托的连接轴到闸瓦外缘（与轮对轮箍踏面相压合的位置）。

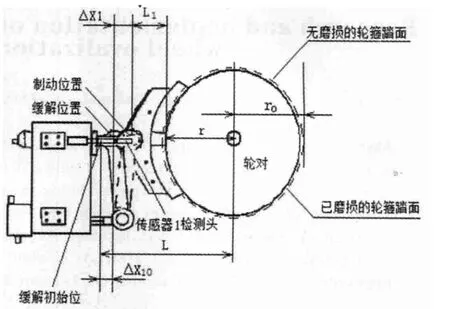
图4 闸瓦磨损的检测及计算参数示意图

闸瓦磨损的厚度Δh通过以下公式推导得出。

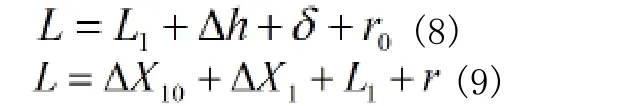
通过以上公式可推导出：

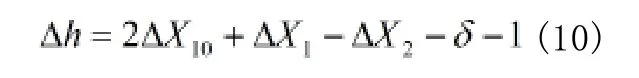
以上L、r0、L1、制动器初始缓解位置等参数通过人机界面触摸屏设定，输入到工控机中。

3 轮对椭圆化检测仿真

对于车轮圆周的不圆顺，本文参考了相应的文献[4]，采用一个长波长周期性车轮非圆化计算方法,建立一个椭圆车轮的数学模型,将车轮半径 视为时间的函数：

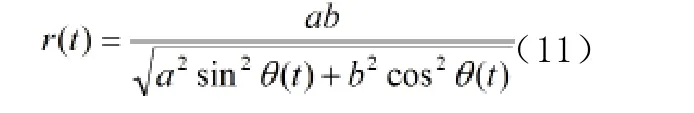
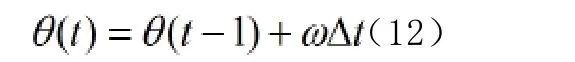
式中， -车轮名义滚动角速度

式（11）、（12）及图5表示了车轮椭圆化模型，轮对的两端车轮在椭圆化过程中常常是不对称的，假设轮对的两个车轮在椭圆化过程中是不对称的，即两个椭圆相位差为，如图6所示。

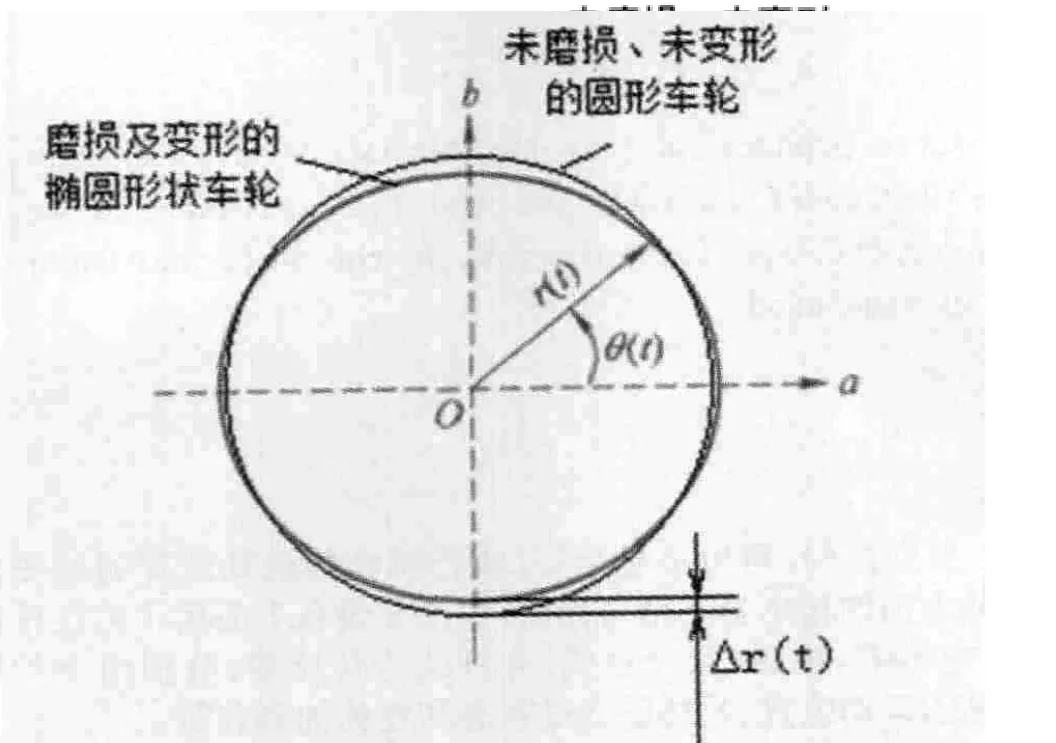
图5 椭圆状车轮计算模型

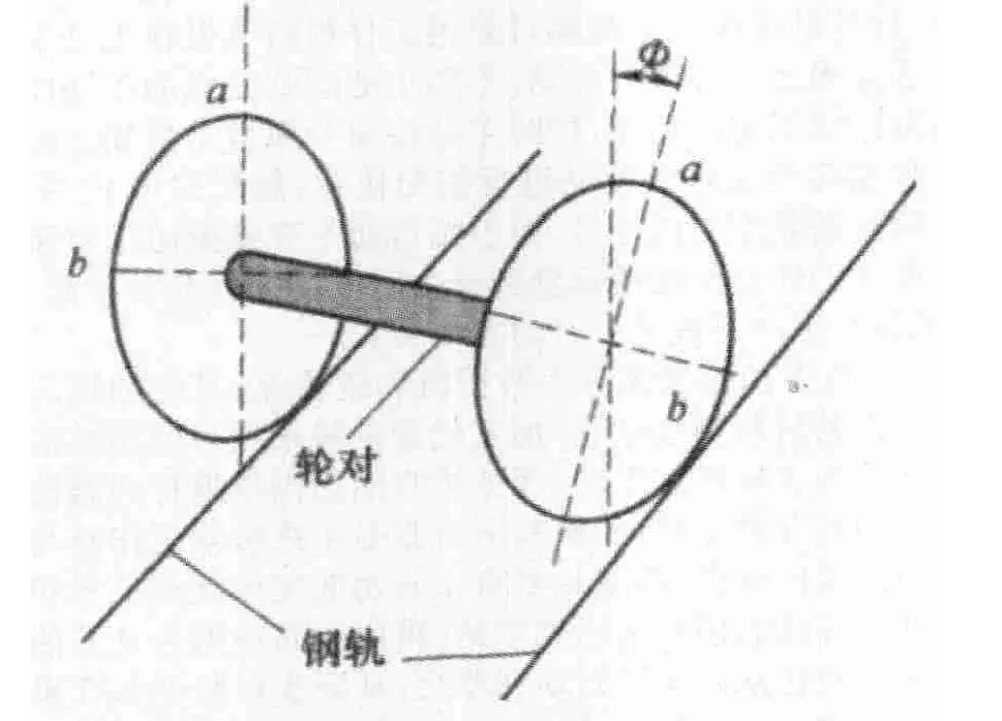
图6 轮对椭圆形状车轮相位角

通过公式（11）、（12）建立数学模型，对a、b、Φ分别赋值为624.5、619.5、6º，电力机车标准车轮半径为625毫米，机车运行速度为100Km/h，利用MATLAB软件进行仿真一对轮对的两个车轮椭圆化程度与Δr（t）的关系，通过Δr（t）的变化来监测车轮的椭圆化程度；仿真图形如图7所示。

图中曲线1、2分别为左、右边车轮Δr（t）的曲线，曲线中波峰值、波谷值分别代表车轮椭圆化中短轴、长轴与标准车轮的差值，分别为5.5mm和0.5mm。

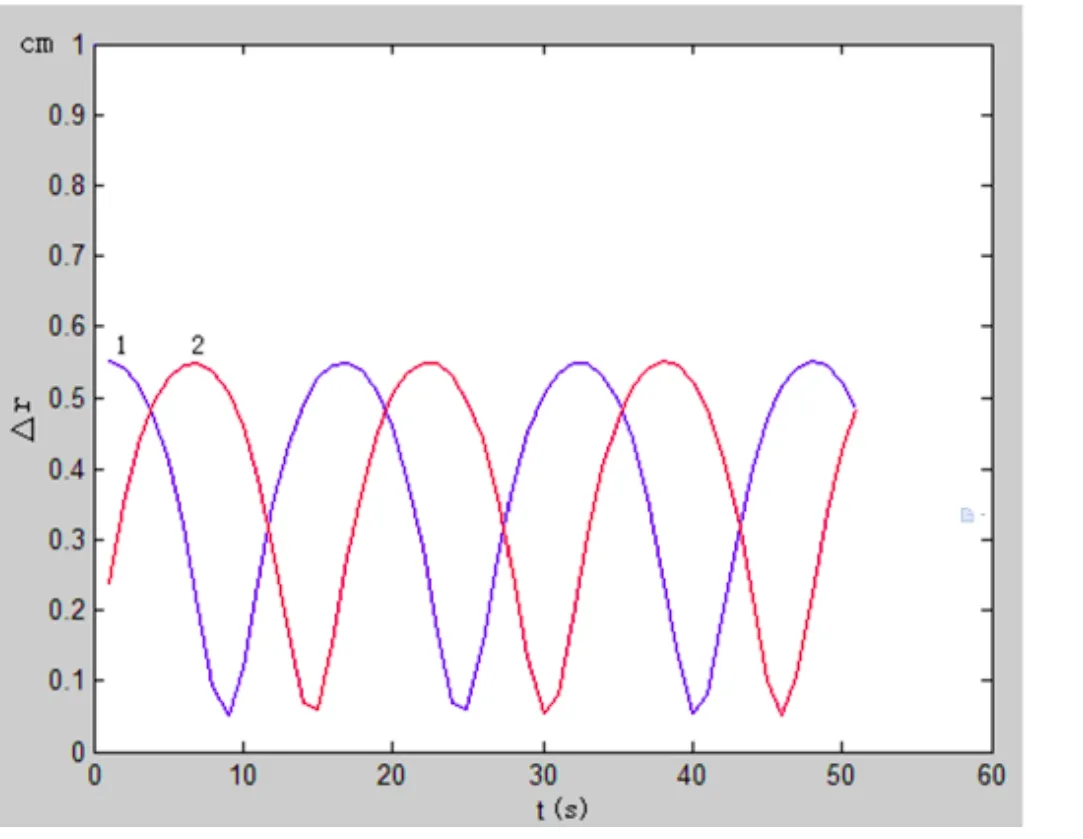
图7 MATLAB仿真曲线

在系统工作时，该数据将实时采集到工控机上并存储，可作为机车轮对在线检测的依据；将椭圆化程度的最大值、最小值及相位差反映到工控机的人机界面上，以提示操作者轮对椭圆化的程度以及两个轮对的相位偏角，如果达到设定的阀值时，将启动声光报警。

4 结论

本设计的传感器采用位移传感器，安装方便，安装尺寸要求不严格，减少了安装的难度，便于量产使用。传感器将位移转换成电流信号，很好的抑制了线路干扰，通过两个位移传感器的信号采集及运算，真正检测到轮对踏面的磨损及轮对椭圆化程度、闸瓦厚度、制动器的缓解状态。

这样可以提示工作人员及时更换轮对，闸瓦，以及检修制动器，避免了此类故障造成的行车事故。

[1] 李益民,电力机车制动机[M].北京:中国铁道出版社,2008.8.

[2] 张雪珊,肖新标,金学松.高速车轮椭圆化对车辆系统行为的影响[J].机械工程学报, 2010,46(16):67-73.

[3] 宋雪臣.传感器与检测技术[M].北京:人民邮电出版社,2009.5.

[4] 张雪珊,肖新标,金学松.高速车轮椭圆化问题及其对车辆横向稳定性的影响[J].机械工程学报, 2008,44(3):50-56.