偏差最小的四心圆近似椭圆作图法

曾振柄， 陈良育， 李志斌， 陈光喜

（1. 华东师范大学软件学院，上海 200062；2. 上海市高可信计算重点实验室，上海 200062；

3. 华东师范大学计算机科学技术学院，上海 200062；4. 桂林电子工业学院计算科学与数学系，广西 桂林 541004）

偏差最小的四心圆近似椭圆作图法

曾振柄1,2， 陈良育1,2， 李志斌3， 陈光喜4

（1. 华东师范大学软件学院，上海 200062；2. 上海市高可信计算重点实验室，上海 200062；

3. 华东师范大学计算机科学技术学院，上海 200062；4. 桂林电子工业学院计算科学与数学系，广西 桂林 541004）

以曲线的等距线距离为度量，得到近似椭圆与精确椭圆的偏差估计，并给出了偏差与半轴长的显示表达式。通过符号计算和回归分析，提出一种偏差最小的四心圆近似椭圆作图法。新方法易于通过尺规作图实现，可用于编制数控机床中加工椭圆零件的插补程序。

四心圆作图法；偏差分析；椭圆；等距线

众所周知，使用直尺和圆规手工作图，不可能画出精确的椭圆。用若干段圆弧拼接成近似椭圆是一个自然的想法。有考证，用一些两两相切的圆弧画椭圆的方法，至少可以追溯到 16世纪文艺复兴时期的建筑师Sebastiano Serlio，甚至可追溯到公元一世纪的罗马竞技场，或者更早于1500多年的巨石圈[1]。椭圆的近似画法数学（制图）、天文（轨道分析）、艺术和建筑（如石拱门）设计中曾有广泛应用。现代计算机字体设计中也经常考虑用圆弧逼近一般的二次或三次曲线。图1(a)是达芬奇(Leonardo da Vinci)的 Hostinato Rigore铭文徽章，其轮廓可用4段圆弧获得非常接近的拟合，图1(b)中显示TrueType字体中用一些圆弧产生字母a的轮廓。

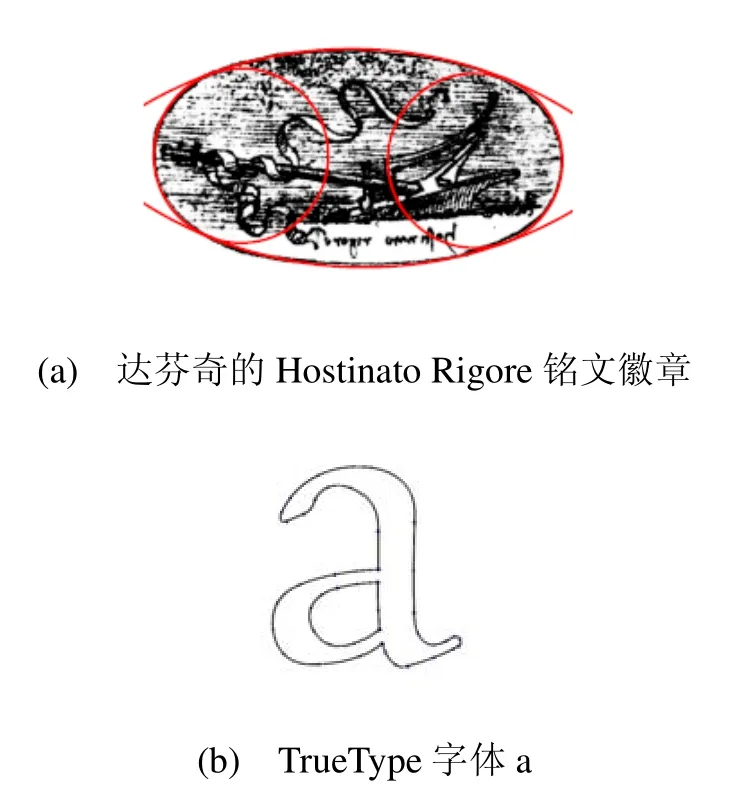
图1 圆弧画椭圆的方法例证

现代画法几何中常用4段圆弧连接画圆的轴测投影。下面的画法1，在要求较低的情况下可用作正等测和正二测椭圆。

画法 1

1） 作椭圆外接菱形。设 O为菱形中心，A, D ,B,C为菱形四边的中点；

2） 作菱形各边的垂直平分线，交于 I, J,K,L四点；

3） 分别以 I , J,K,L为中心， IA, J B, KC, LD为半径画弧 AC ,B D,CB,DA，四段圆弧构成一近似椭圆。

图2画的是正等测椭圆，轴间角等于120°，K,L与菱形的顶点重合。这种近似椭圆的长半轴比真实椭圆的短，短半轴比真实椭圆的长。设θ是轴间角。计算可知，真实椭圆的长半轴和短半轴分别是

图2 画法几何中的近似椭圆

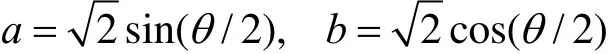
而近似椭圆中，

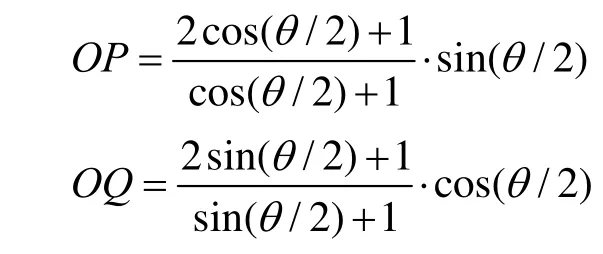
易知，当 90° ＜ θ＜ 180°时，

在正等轴测图中，

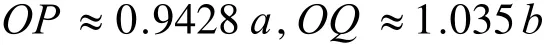
已知椭圆的长半轴和短半轴，可用下面的四心圆法画近似椭圆。它作出的图形光滑，偏差较小，容易用尺规和手工实现作图。画法如下：

画法2 设椭圆T的长轴是AB，短轴是CD，O是AB和CD的交点，如图3所示。

1） 连接AC。在AC上取点E使CE=OAOC；

2） 作AE的中点F，过F作AE的垂线交AB于G，交CD于J。在OB上取点H使OH=OG，在OC上取点I使OI=OJ；

3） 以G为圆心，GA为半径画弧K4AK1，以J为圆心，JC为半径画弧K1CK2，以H为圆心，HB为半径画弧K2BK3，以I为圆心，IB为半径画弧K3DK4。则圆弧K4AK1，K1CK2，K2BK3，K3DK4组成的图形Γ近似于椭圆T。本文称Γ为四心圆近似椭圆。

图3 四心圆近似椭圆

许多文献载有画法2。文献[2-3]给出将画法2用于数控机床中加工椭圆形零件的插补程序。文献[4]分析了用四心圆法作的近似椭圆与精确椭圆之间的偏差，得出以下结论：

1） 近似椭圆与精确椭圆的偏差在大圆弧段较小，在小圆弧段较大；

2） 近似椭圆的面积比精确椭圆的面积略大；

3） 椭圆越扁平，偏差越大。

本文用符号计算推导了近似椭圆的偏差公式，并给出一种偏差更小的四心圆近似椭圆作图法。

1 四心圆近似椭圆的偏差

本文所称四心圆法指画法2。下面的引理描述四心圆近似椭圆与精确椭圆的位置关系，这个结果见第 3.1节[4]。为方便后面的讨论，本文给出其证明。

引理1 设T是椭圆，Γ是对应的四心圆近似椭圆。则除椭圆的4个顶点外，近似椭圆Γ与椭圆T有4个公共点 M1,M2,M3,M4，分别位于4段椭圆弧 AC ,C B,BD,DA上，近似椭圆上的弧M1C M2,M3DM4位于椭圆 T 的内部，弧M4AM1,M2BM3位于椭圆T的外部。

证明 假设 AB =2a ,CD=2b。则椭圆T的方程是

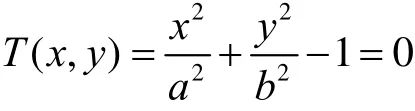
易计算 JGFE ,,, 的坐标分别是

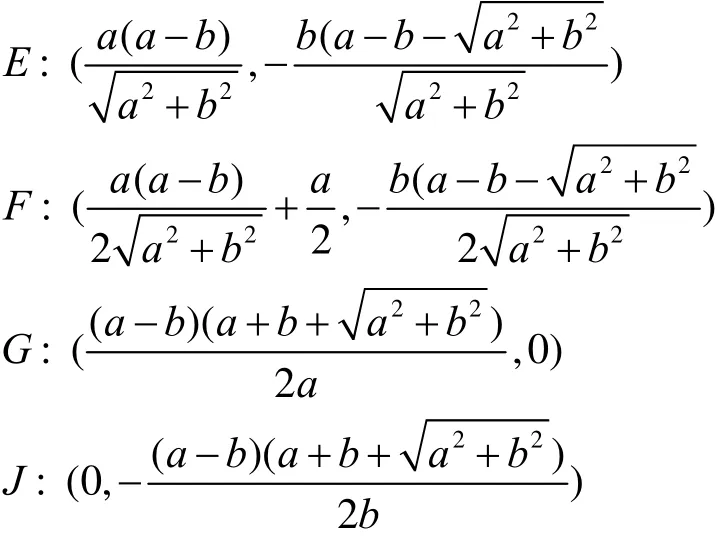
令 O (G ,A)是以G为圆心，GA为半径的圆；O (J ,C)是J为圆心，JC为半径的圆。这两个圆的方程分别是

计算可知点1K的坐标是

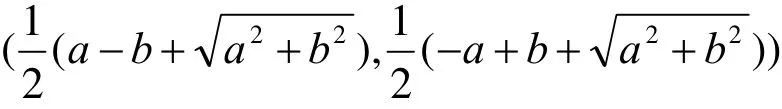
易验证

所以，点K1在椭圆T的外部。

下证除点A以外，圆弧14AKK 在椭圆的外部。为此，计算圆 ),( AGO 与椭圆T的交点，得

其中A是一个二重交点。因

知弧14AKK 与椭圆T的交点只有A，又因K1在T的外部，所以除点A以外，弧14AKK 在T的外部。

下面证明，除点C以外，弧21CKK 与椭圆T有两个交点。计算圆 ),( CJO 与T的交点，得

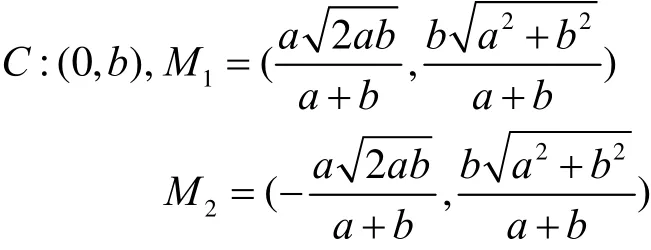
其中C是一个二重交点，21,MM 是一重交点。因

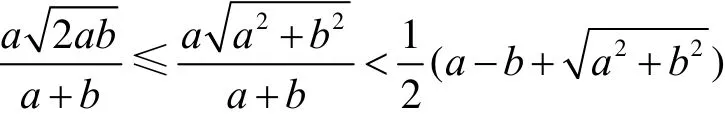
如果在计算四心圆近似椭圆偏差时，用椭圆T上的点 (x , yT)和近似椭圆Γ上的点 (x , yC)的纵坐标之差 Δy =yT-yC作为度量，则该度量与坐标系有关。如下例：设精确图形是C1:x2+ y2-a2=0，近似图形是 C2:x2+ y2-(a + ε)2= 0，ε ＞ 0。则：当 x →0时，Δ y →-ε；当 x→ a时，Δy →-。但撇开坐标系来看，C1与 C2的偏差是均匀的，C1与 C2的曲线距离是ε。用曲线间距离度量曲线逼近的偏差，优点是与坐标系无关。设 C1,C2是两条平面曲线。则C1,C2的距离定义如下[5]

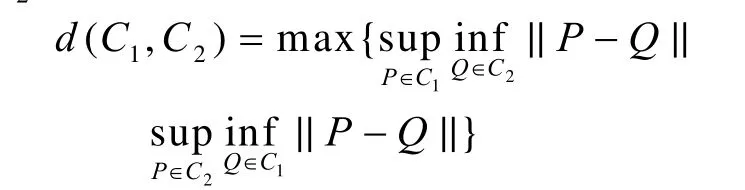
其中 ||P - Q||是点P到Q的距离。d (C1,C2)可用作度量 C2对于 C1的拟合程度。但是很多时候d (C1,C2)的解析表达式不易计算。对于一些特殊的情况，曲线距离可通过曲线的等距线来计算[6]：令K+(C1,a),K-(C1,b)是曲线 C1上的每点分别沿 C1在该点法线的正负两个方向移动距离 a,b所得到的点的轨迹，称为 C1的等距线，令K (C1,a,b)表示这两个等距线围成的图形。则

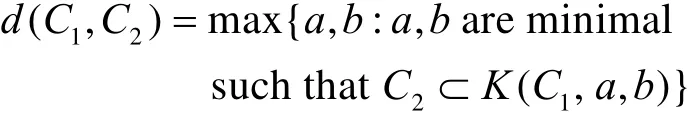
下面计算四心圆近似椭圆Γ和精确椭圆 T之间的距离。按照对称性，只考虑第1象限的图形。令L1是线段 GK1与椭圆T的交点。按引理1，椭圆弧 AL1包含在扇形 GAK1内，因此存在最小的正实数 r0使图形 K(A K1,0,r0)包含椭圆弧AL1；椭圆弧 L1C与圆弧 K1C交于点 M1,C，L1M1包含在扇形 L1JM1内， M1C在扇形 M1JC之外，因此，存在最小的正实数 r1,r2使图形K(K1C ,r1,r2)包含椭圆弧 L1C。令

其中 JPGP, 表示线段的长度。则

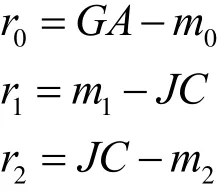
有下面的引理。

引理2 设椭圆T的长半轴为a，短半轴是b，Γ是用四心圆法作的近似椭圆。则

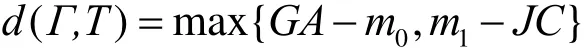
证明 考虑以 J为圆心，m为半径的圆O(J,m)

显然，当 CJm= 时及1mm= 时， ),(mJO 与椭圆T相切。若 ),( yx 是 ),( mJO 与T的切点，则 yx,除满足 ),(mJO 和T的方程外，还满足下面的条件

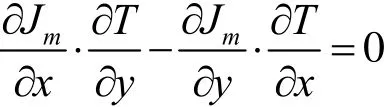
即

通过本文的分析,已经初步发现浮标站和周边站点一些定性定量的规律,未来将进一步找出浮标站与周边站点之间的风力关系,得到由陆地风推导出江面风的理论或半经验结论,应用于日常业务工作。

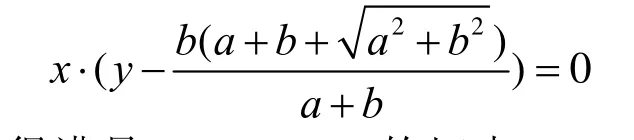
由此解得满足 0,0 ＞＞ yx 的切点 ),( yx 和相应的m

C:(0,b)，

P1:(x1, y1)，

其中

比较点1P和1M 的纵坐标

知1P位于椭圆弧 CM1及

现在求2m。由以上计算知，对任意 0＞m ，圆 ),(mJO 与椭圆T的弧11ML 不相切，从而，定义于圆弧11ML 上的函数

关于点P的横坐标x单调递增，

即

以下计算0m。考虑以G为圆心，以m为半径的圆 ),( mGO

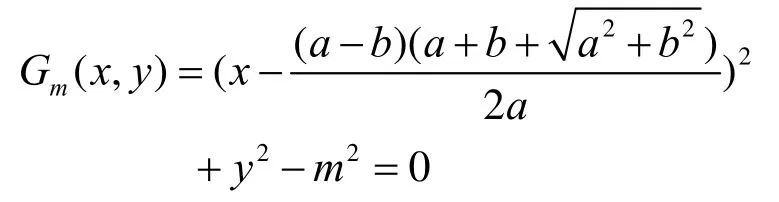
当 GAm= 时， ),(),( AGOmGO = 与椭圆T在点A相切。我们求使 ),( mGO 与T相切的其它m及相应的切点。如果有唯一的 GAm＜ 使切点位于椭圆弧1AL，则该m即是0m。 ),( mGO 与T在第1象限的切点 ),( yx 满足

解之得

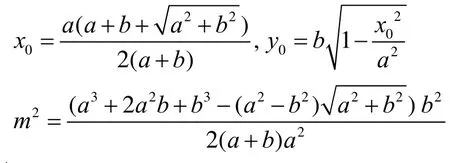
易验证

上式之右是1K的横坐标。设1L的坐标是 ),(llyx 。则

于是，使 ),( mGO 与椭圆T相切的 GAm＜ 是唯一的，且切点 P0:( x0,y0)位于椭圆弧 AL1。此证明

因此，定义于圆弧1AN上的函数

连续可微，且对1AN上一切P满足

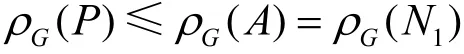
故m0=min ρG(P)，特别

最后，得到

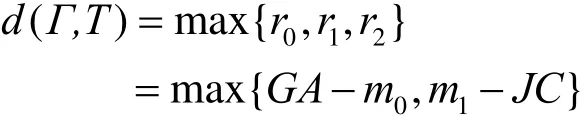
引理2得证。

现在我们可以给出四心圆近似椭圆的偏差公式。

定理1 设 ba,是精确椭圆T的长半轴和短半轴，Γ是用四心圆作的近似椭圆，则

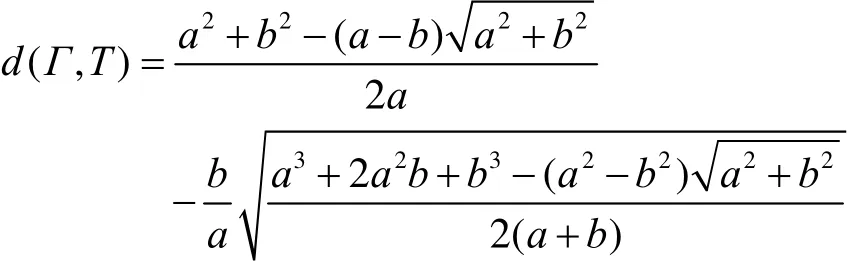
证明 计算可得

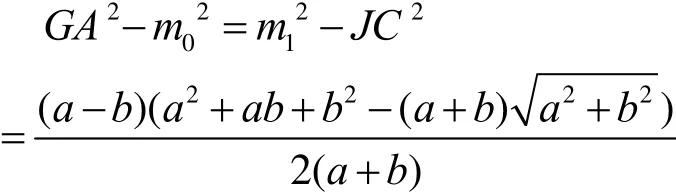
又易见

所以

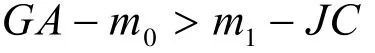
定理1得证。

下面将近似椭圆位于精确椭圆以外的偏差称为外偏差，位于精确椭圆以内的偏差称为内偏差。则由引理2和定理1，可得到如下结论：

1） 最大内偏差出现在大圆弧段 P1处，最大外偏差出现在小圆弧段P0处。其中10,PP 的坐标见引理2证明。外偏差和内偏差之比为

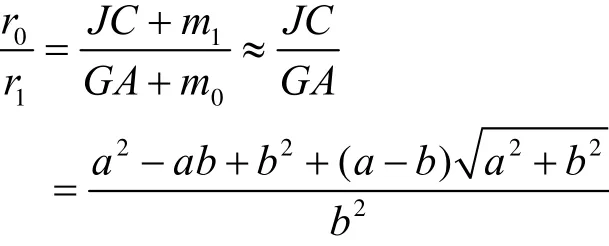
2） 最大偏差可近似如下表示为 ba,的表达式

其中

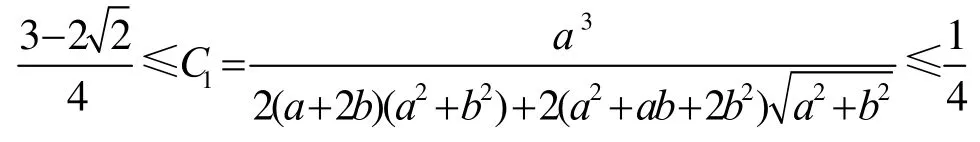
3） 当 a =1，b的值从0增加到1时，偏差d( Γ, T )≤ 0.027678…，最大偏差当 b=0.22432…时取到。图4画出 a =1，0 ≤ b≤ 1时 d (Γ ,T)的曲线。

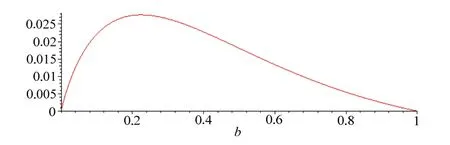
图4 四心圆近似椭圆的最大偏差

4） 若将偏差跟短半轴b相比，则椭圆越扁平，相对偏差越大。即当 1=a ，b接近0时，

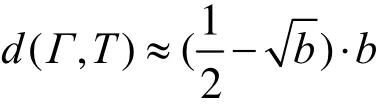
可以看出，将曲线之间的距离作为逼近偏差的度量，得出的实际上是最大偏差。若将近似曲线和真实曲线围成的图形的面积作为偏差的度量，可以得到逼近的平均偏差。文献[4]指出，近似椭圆的面积大于精确椭圆的面积。因为近似椭圆的有些弧段在精确椭圆内，有些弧段在精确椭圆外，所以近似椭圆和精确椭圆围成的图形的面积 ),( TΓS 大于近似椭圆的面积与精确椭圆的面积之差。过1M 作直线1xx= ，过1K 作直线x= xK，将近似椭圆Γ和椭圆T围成的图形在第一象限的部分分成3块，其面积自左向右分别记为W1,W2,W3。令

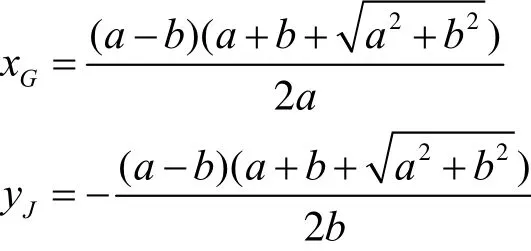
则

用符号计算软件Maple可将321,, WWW 和 ),( TΓd表示为 ba,的函数。这些表达式过于复杂，此处仅画出当 1=a ，0 1b≤ ≤ 时 ),( TΓd 的图形，如图5所示。

图5 画法2的四心圆近似椭圆的面积偏差

2 偏差更小的四心圆近似椭圆

四心圆椭圆近似作图法可以一般化为如下曲线逼近问题。假设要画的椭圆T是

其中心为 O，顶点为 A ,B ,C,D，坐标分别为A = (a ,0),B = (0,- a), C = (0,b), D = (0,- b)在长半轴OA上取一点 G( u ,0),(0 ≤ u ＜a)，在短半轴或其延长线上取点 J (0 ,- v),(v＞0)，以 G为圆心，GA为半径画圆 O (G ,A)，以 J为圆心，JC为半径画圆 O (J,C)。如果两圆与射线JG交于同一个点 K，则二圆在点 K是 1阶切触。圆弧AK,K C构成椭圆在第1象限的一个近似，如图6所示。按对称方法作椭圆在其它象限的近似。记近似椭圆为Γ。这样的作图是可能的，例如，取

就得到画法2。易观察到，只要 vu,满足下列关系

则 O (G ,A)和 O (J,C)与射线JG的交点重合。设d (Γ ,T)是近似椭圆和真实椭圆之间的距离。如何选择 u,v使得曲线距离 d (Γ ,T)为最小？

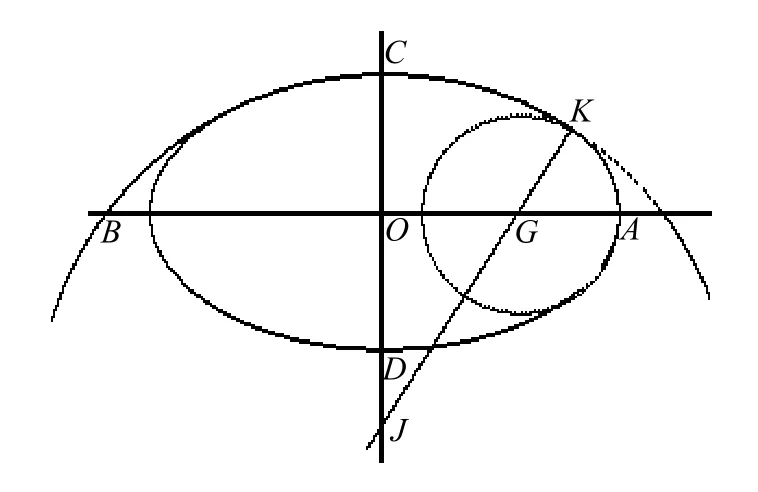
图6 一般的四心圆椭圆

这个问题是一个单参数系统的优化问题。可验证， vu,满足的条件可写成下面的单参数形式

圆 ),( AGO 和 ),(CJO 的方程是

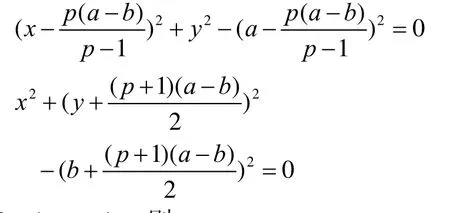
设K= (xk,yk)，则

为使G在OA上，以及K在第1象限，参数p应满足条件 /p a b≥ 。为保证点K落在椭圆T的外部，p还须满足下面的不等式

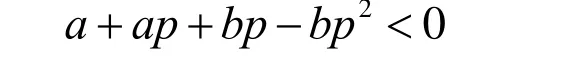
令M=(xm,ym),N=(xn,yn)分别为圆 O(J ,C)和 O (G ,A)与椭圆的交点。则

注意，当 a + ap+bp-bp2＜0时总有 a + bbp＜ 0，以及

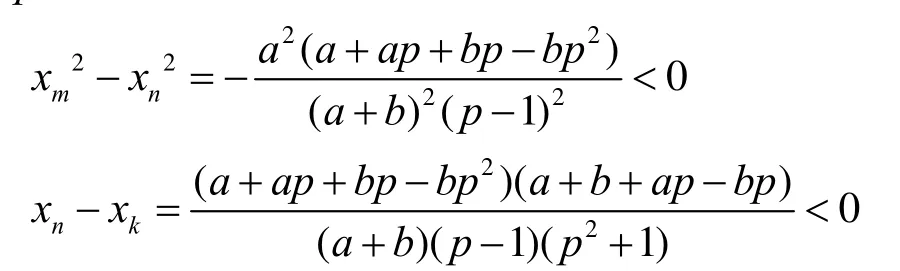
因此椭圆T在第1象限与近似椭圆Γ有 CMA ,, 3个公共点，椭圆弧CM在近似椭圆Γ外部，椭圆弧MA在Γ的内部。椭圆T与圆 ),( AGO 的交点N在弧MA上，如图7所示。

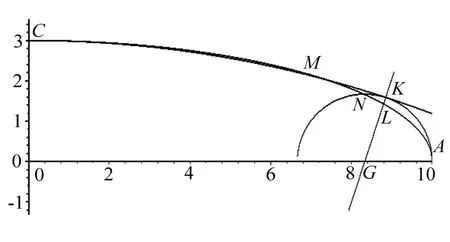
图7 第1象限的近似椭圆

下面计算 ),( TΓd 。设L是椭圆T与GK的交点。如第2节所证，

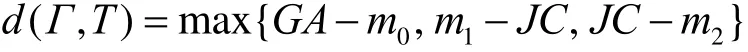
其中

令P0=(x0,y0),P1=(x1,y1),P2=(x2,y2)分别是取到极值 m0,m1,m2的点。用引理2证明中的方法可求得

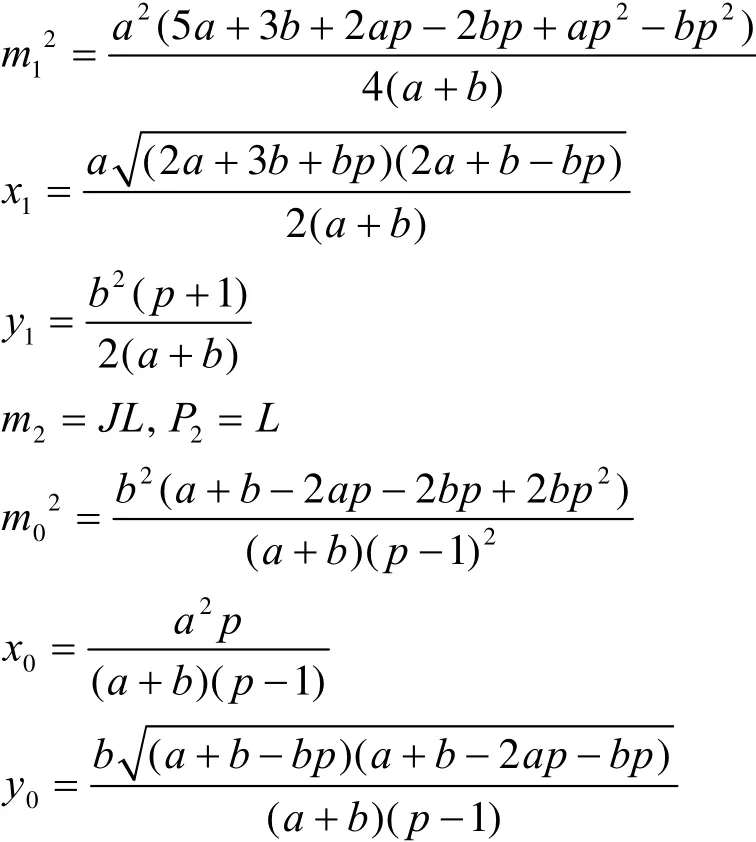
容易验证

此说明 P0,P1分别位于椭圆弧段 AL,M C上。因此m2=JL＞JP0=m0，即

d( Γ, T ) = max{G A- m0,m1-JC}

其中 GA ,J C,m0,m1可以看成 a ,b ,p的函数。注意到p满足的条件可写成

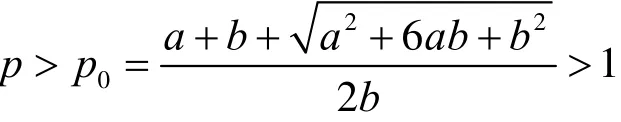
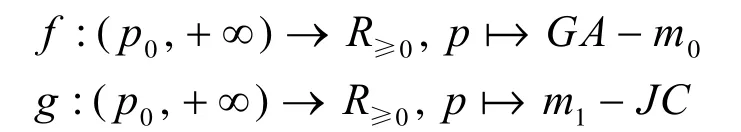
有下面的结果。

定理 2 对任何0 ＜ b ≤ a，存在实数 p*, p0＜ p* ＜ p1使

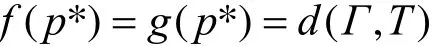
证明 可验证 f,g满足以下性质：

1） 函数 f (p)在其定义域单调增加；

2） 函数 g (p)在区间 ( p0,p1)单调减少；

3） f ( p1)＞ g(p1)，且当 p趋近 p0时，f( p )＜ g(p)。此处不详列推导过程。

图8画出 a = 5, b=4时函数 f,g 在区间p0=2.711…和p1=2.850…之间的图形。 可知，此时 p* ≈2.75相应的 d ≈0.02123；而 p1相应的d ≈0.02718。我们得到比画法2的偏差更小的四心圆近似椭圆。

图8 当 a = 5, b = 4时取 p* ≈2.75得到偏差最小的近似椭圆

图9画出当 a =1，0 ≤ b≤ 1时 p0b, p *b,b, p1b的曲线。其中，p是 p*的一个回归

图9 曲线 p *(b)决定最佳近似椭圆， (b)为其拟合曲线

图10 误差曲线

图10中的曲线自上而下是当 a =1， 0 ≤ b≤ 1时 p1对应的四心圆近似椭圆和,p*对应的四心圆近似椭圆与精确椭圆的偏差。从图中可以看出，取参数p=的近似椭圆的最大偏差接近最佳参数 p*对应的画法的偏差，比画法2有明显降低。计算知，新画法最大偏差小于0. 01145，发生在 b /a ≈0.28时。

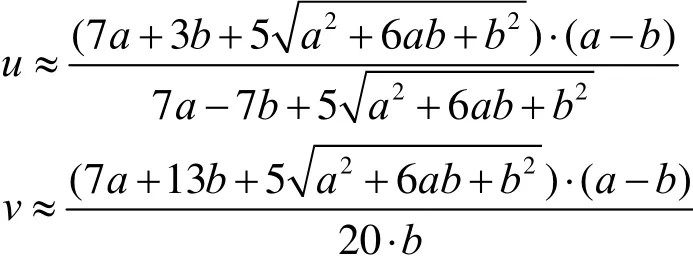
从而可用于确定G和J的坐标，实现新的四心圆画法，而上述表达式中所涉及的运算都是尺规作图容易实现的。

3 结 论

本文显示，原有的四心圆椭圆近似画法有改进的余地。新画法可用手工实现。与画法2一样，新画法作出的近似椭圆在4个顶点处的曲率有误差。新画法作出的近似椭圆，在大圆弧段和小圆弧段与精确椭圆的偏差相等，比画法2的近似椭圆，有更多部分含在精确椭圆内部，或许使之不适合用于数控机床加工椭圆形状的零件。可用类似方法寻求偏差尽可能小的包含精确椭圆近似椭圆。

文献[7]中，P. L. Rosin给出四心椭圆的改进画法。该结果用本文记号可表示为

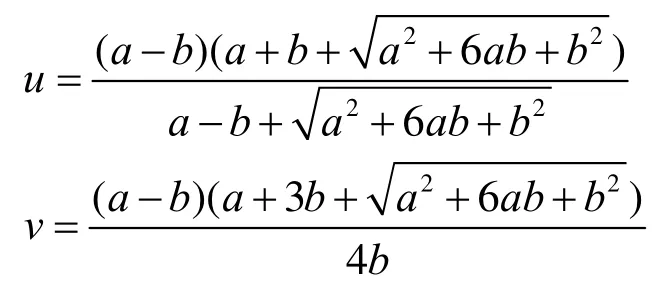
文献[8]给出计算机程序，对于给定的 a,b，通过调整 K1,K2,K3,K4的位置使得近似椭圆在大弧段和小弧段的误差相等，从而可以得到更好的近似。文献[9]根据图形分析确定了四心圆弧拟合椭圆的定解区间，导出了拟合椭圆的四心圆弧法向误差解析式，并根据法向误差确定了四心圆弧拟合椭圆的最小误差带和最高拟合精度。本文通过回归获得的p是最佳四心圆椭圆的近似公式，在其它文献中未见到。

文献[10]介绍了一种八心近似椭圆画法，可以保证近似椭圆经过椭圆的4个顶点，并且在顶点处有正确的曲率半径。关于用多段圆弧拟合椭圆的算法，还可参见文献[1,11-12]。

[1] Rosin P L, Pitteway M L V. The ellipse and the five-centred arch [J]. The Mathematical Gazette, 2001, 85(502): 13-24.

[2] 张先虎. 机械制图及微机绘图[M]. 北京: 机械工业出版社, 1998: 1-339.

[3] 宋光亭. 近似椭圆的数值计算[J]. 机械工程师, 2001, (1): 24-24.

[4] 王林鸿, 陈永辉. 用四心圆法作近似椭圆的偏差分析[J]. 机械工程师, 2002, (8): 59-60.

[5] Gruber P M. Approximation of convex bodies [C]// Gruber P M, Willis J M. Convexity and Its Application. Basel, Boston, Stuttgart: Birkhäuser Verlag, 1983: 131-162.

[6] Alexandrov A D, Reshernyak Yu G. General theory of irregular curves [M]. Dordrecht, Boston, London: Kluwer Academic Publishers, 1989: 1-300.

[7] Rosin P L. A survey and comparison of traditional piecewise circular approximations to the ellipse [J]. Computer Aided Geometric Design, 1999, 16: 269-286.

[8] Qian W, Qian K. Optimising the four-arc approximation to ellipses [J]. Computer Aided Geometric Design, 2001, 18(1): 1-19.

[9] 唐立波, 张 旭, 李宝良. 四心圆弧拟合椭圆的解析算法及其最优解[J]. 大连交通大学学报, 2009, 30(4): 18–21.

[10] 钱可强. 画法几何学[M]. 李名纪译. 福州: 福建科学技术出版社, 1984: 1-204.

[11] Eberly D. Approximating an ellipse by circular arcs [EB/OL].http://www.geometrictools.com/ Documentation/ApproximateEllipse.pdf, 13, Jan. 2002/12, Feb. 2008.

[12] Banchoff T, Giblin P. On the geometry of piecewise circular curves [J]. The American Mathematical Monthly, 1994, 101(5): 403-416.

Approximating ellipse using four-arcs with the smallest error

Zeng Zhenbing1,2, Chen Liangyu1,2, Li Zhibin3, Chen Guangxi4
( 1. Software Engineering Institute, East China Normal University, Shanghai 200062, China; 2. Shanghai Key Lab of Trustworthy Computing, Shanghai 200062, China; 3. Computer Science & Technology School, East China Normal University, Shanghai 200062, China; 4. Department of Computing Science & Mathematics, Guilin University of Electronic Technology, Guilin Guangxi 541004, China )

The distance of equidistant curves is used to estimate the errors between an ellipse and the four-arcs which approximate the ellipse. An explicit expression of the errors and the semi-axes of the ellipse are established. A new method is proposed for approximating an ellipse by using of four-arcs with minimal error via symbolic computation and regression analysis. Our method is easy for drawing with ruler and compass and can be used in interpolation programming for the computerized Numerical Control lathes.

four-arcs; error analysis; ellipse; equidistant curve

TH 126

A

2095-302X (2013)01-0009-08

2011-08-08；定稿日期：2011-10-12

国家自然科学基金资助项目（61021004）；上海市重点学科资助项目（B412）；上海自然科学基金资助项目（11ZR1411500）

曾振柄（1963-），男，甘肃皋兰人，教授，博士，主要研究方向为数学机械化、定理机器证明。E-mail：zbzeng@sei.ecnu.edu.cn