不同圆角过渡的3A21铝合金矩形管弯曲壁厚变化与损伤研究

周书辉， 刘郁丽， 沈化文， 杨 合

(西北工业大学凝固技术国家重点实验室，西安710072)

在矩形管弯曲过程中，中性层外侧由于受到切向拉应力作用而产生拉伸应变，使管材外侧壁厚减薄。矩形管壁厚的减薄与材料内部组织劣化产生的损伤有关，当损伤值累积到一定程度时，壁厚减薄严重最终产生断裂。壁厚变化与损伤不仅与矩形管弯曲成形过程的工艺条件有关，而且与管材的截面形状有关。矩形管由于棱边的存在，使得靠近棱边处的材料流动受到约束，其材料流动并不均匀。而当矩形管的棱边采用不同的圆弧过渡时，截面形状发生变化，使其在弯曲过程中金属流动情况发生变化，导致壁厚减薄以及损伤的分布也在发生变化。因此有必要从改善材料流动性入手，研究棱边处采用不同圆弧过渡时矩形管的壁厚变化和损伤情况，为管材弯曲件不同截面形状的选择提供参考。

近年来，很多学者对管材弯曲过程中的壁厚变化和损伤破裂做了大量研究，其中对于壁厚变化的研究，大多数是研究不同成形参数对壁厚分布的影响。张津等［1］分析了矩形弯管件的壁厚分布规律，矩形管绕弯几何、材料参数对壁厚变化的影响。鄂大辛等［2，3］通过有限元模拟，研究了圆管弯曲过程中壁厚变化规律以及壁厚变化对最小相对弯曲半径的影响。岳永保等［4］采用实验法，对小弯曲半径薄壁圆管弯曲过程中的壁厚减薄进行了研究，发现合理增加压块速率有利于控制壁厚减薄。对于管材壁厚减薄严重产生的断裂现象的研究，大多数是基于损伤思想，通过建立合理的韧性断裂准则的方法来实现。在众多韧性断裂准则中，Lemaitre准则与材料弹塑性行为全耦合，预测准确性较高，因此应用较为广泛［5～8］。Li等［9］通过单向拉伸试验获得了Lemaitre准则的损伤参数，通过模拟获得了5052O铝合金圆管数控弯曲临界壁厚减薄量。Zhan等［10］基于Lemaitre损伤理论建立了圆管数控弯曲有限元模型，研究了弯曲半径和助推速率对钛合金管数控弯曲过程中损伤变量的影响规律。目前对于壁厚变化和损伤的研究大多数还是以圆管为研究对象，而矩形管的形状不是自支撑的，材料流动情况更为复杂，不能直接套用圆管结果。为此本工作利用ABAQUS/Explicit的VUMAT二次开发平台，将Lemaitre韧性断裂准则嵌入管材弯曲有限元模型，研究了带有不同圆角的3A21铝合金薄壁矩形管的壁厚变化及损伤情况。

1 Lemaitre韧性断裂准则

Lemaitre损伤准则在工程应用中最为广泛，适用于大多数弹塑性延性损伤的金属材料［11］。该准则定义了损伤变量D，用来量化表征材料的受损程度。在此基础上，Lemaitre基于连续介质热力学，建立了一种各向同性的损伤演化形式［12］，如式(1)所示。

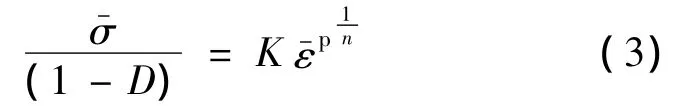
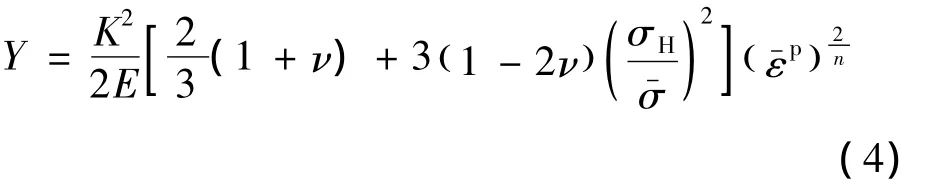
将式(4)代入式(1)，得到损伤演化方程为

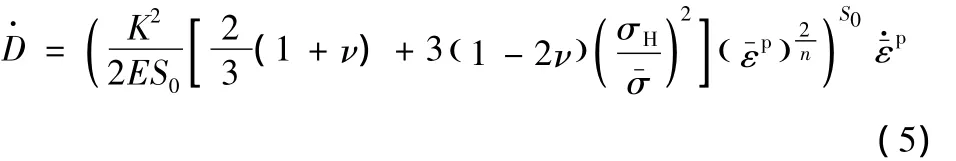
大量研究发现，当塑性应变较大时，可以近似认为S0=1，同时Lemaitre引入了损伤材料参数Dc，εR和εD，此时式(5)转换为

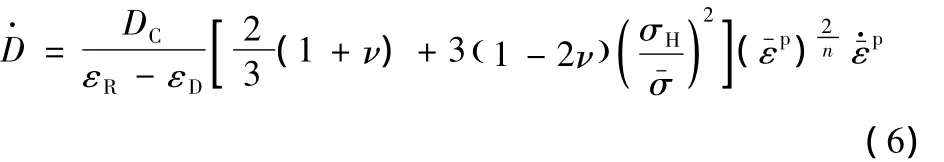
式中，Dc是损伤阈值，εR是材料断裂时的应变，εD是材料开始出现损伤时的应变。为了便于数值计算，Lee［13］把式(6)进一步修改为式(7)所示的增量形式

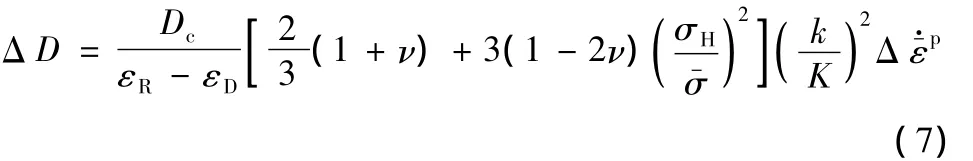
式中k是材料流动应力。式(7)即为Lemaitre准则的增量形式，即随着塑性应变的增加，损伤值D不断累积，当材料损伤值到达损伤阈值Dc时，认为材料发生破裂。

2 有限元模型的建立

2.1 材料模型的建立

2.1.1 Lemaitre准则中材料参数的获取

3A21铝合金薄壁矩形管的损伤参数εD，εR和Dc可以基于弹性模量变化法［13］来获取。即采用标准拉伸试样进行反复加载、卸载试验并结合数值模拟的方法获得。材料进行反复加载卸载时，各次卸载时损伤弹性模量可用式(8)表示。

进而由式(8)可得各次卸载时的损伤值D，如式(9)所示。

从3A21铝合金薄壁矩形管上截取标准拉伸试样进行反复加载卸载试验，得到不同应变下的弹性模量˜E，如图1a所示。将试验值代入式(9)得到如图1b所示的不同应变下的损伤值。由图可知，当应变小于0.018时，损伤值呈线性增加，当应变大于0.018时，损伤值随塑性变形的变化趋势趋于平缓。对数据点进行分段线性拟合，当损伤值D=0.189时，其随应变的增加不再变化，因此取损伤阈值Dc=0.189。εD的值为损伤开始时的应变值，即当D=0时所对应的应变值，由图中所拟合的曲线可得εD=0.0012。

由于Lemaitre准则中损伤参数εR为断裂处的应变，而试验中的应变是采用引伸计来测量标距内的应变，因此获得的εR值并不准确。为了得到材料断裂处应变值εR，采用与试验相同的加载条件在ABAQUS中对试样拉伸过程进行数值模拟。图2所示为模拟中试样出现颈缩时的应变分布，由图可知颈缩处的最大应变为0.399，而此时拉伸位移为22.7mm，试验中材料断裂时拉伸位移约为23mm，且断裂前并未发生明显的颈缩现象，如图3所示。模拟结果与试验结果基本一致，可以认为此时的应变即为断裂时的真实应变，即εR=0.399。对3A21铝合金薄壁矩形管进行有限元数值模拟时所用到的材料参数与损伤参数如表1所示。

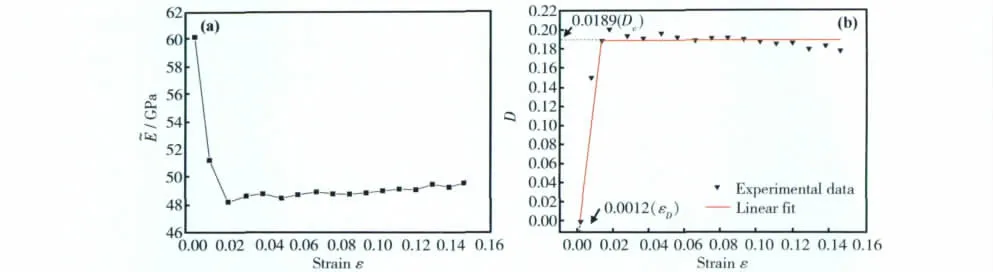
图1 3A21铝合金矩形管弹性模量与损伤值随应变变化图 (a)弹性模量;(b)损伤值Fig.1 Variational law of Young'smodulus and damage value with strain of 3A21 thin-walled rectangular tube (a)Young'smodulus;(b)damage

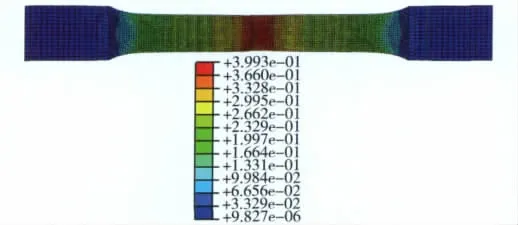
图2 拉伸试样应变分布的模拟结果Fig.2 Strain distribution of tension specimen

图3 试样断裂后的形貌Fig.3 Experimental result of fractured specimen

表1 3A21铝合金薄壁矩形管材料常数及损伤参数Table 1 Material and damage properties of3A21 thin-walled rectangular tube

2.1.2 Lemaitre准则的嵌入

ABAQUS提供了VUMAT二次开发平台，供用户嵌入自己的材料子程序。本工作利用显式算法，采用Mises屈服准则，各向同性硬化法则，用Fortran语言开发耦合了Lemaitre准则的材料子程序并将其嵌入矩形管弯曲有限元模型。

耦合Lemaitre准则的材料本构关系子程序具体计算步骤如下。

(1)弹性预测

假设变形初始为弹性变形，塑性应变增量为零，由广义虎克定律计算试探应力，如式(10)所示。

式中下标(i)表示应力更新前变量值，(i+1)表示应力更新后变量值。试探应力的偏张量为:

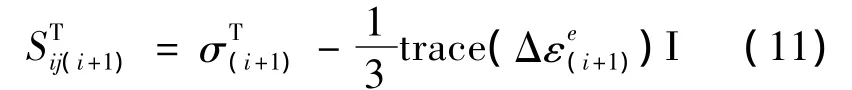
(2)屈服条件检查

将弹性预测阶段得到的试探应力的偏张量式(11)代入所示的耦合了损伤的屈服准则，如式(12)所示。

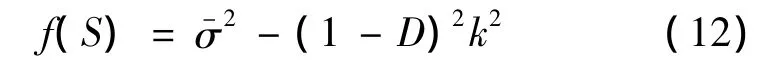
若f(S)≤0，则表明矩形管弯曲成形处于弹性变形阶段，此时更新状态变量。否则进入塑性修正阶段。

(3)塑性修正

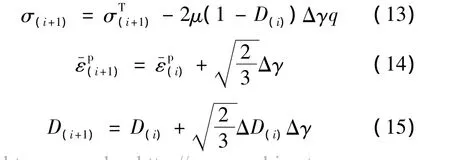
计算流程如图4所示。

图4 Lemaitre准则数值化计算流程Fig.4 Flow chart of subroutine coupling Lemaitre criterion

2.2 有限元模型的建立

基于动态显式ABAQUS/Explicit软件平台，针对壁厚为1mm，高度为12.2mm，宽度为24.86mm，圆角半径分别为5mm，4mm，3mm和2mm的矩形管(如图5所示)弯曲过程进行有限元建模。模具由弯曲模、夹块、防皱块、助推块以及芯模组成。在成形过程中模具变形很小，故将模具简化为刚性体，采用壳单元对其进行划分。带圆角的矩形管为变形体，采用C3D8R实体单元对其进行描述，该单元为八节点六面体减缩积分单元，能够以较低的计算成本获得精度较高的结果。为避免加载速率不连续带来的动态效应，对于弯曲模、夹块、助推块采用图6所示的光滑幅值曲线来描述其加载进程。

基于以上条件，本工作建立了弯曲半径均为1.6H(H为矩形管的高度)的不同圆弧过渡的矩形管弯曲过程三维有限元模型，弯曲角度均为90°。考虑到模型结构和载荷的对称性，仅取整体结构的一半进行模拟分析，由于篇幅所限，本工作只给出圆角半径为4mm的矩形管弯曲有限元模型示意图，如图7所示。模拟条件如表2所示。在弯曲过程中，管材在夹块的夹持下绕弯曲模转动，同时助推块以相应的速率推动管材向前移动。模拟时采用图6所示的光滑幅值曲线对夹块、弯曲模、助推块施加速度载荷，即在加载和卸载时平滑过渡至设定速率，以避免加速度不连续所带来的冲击。

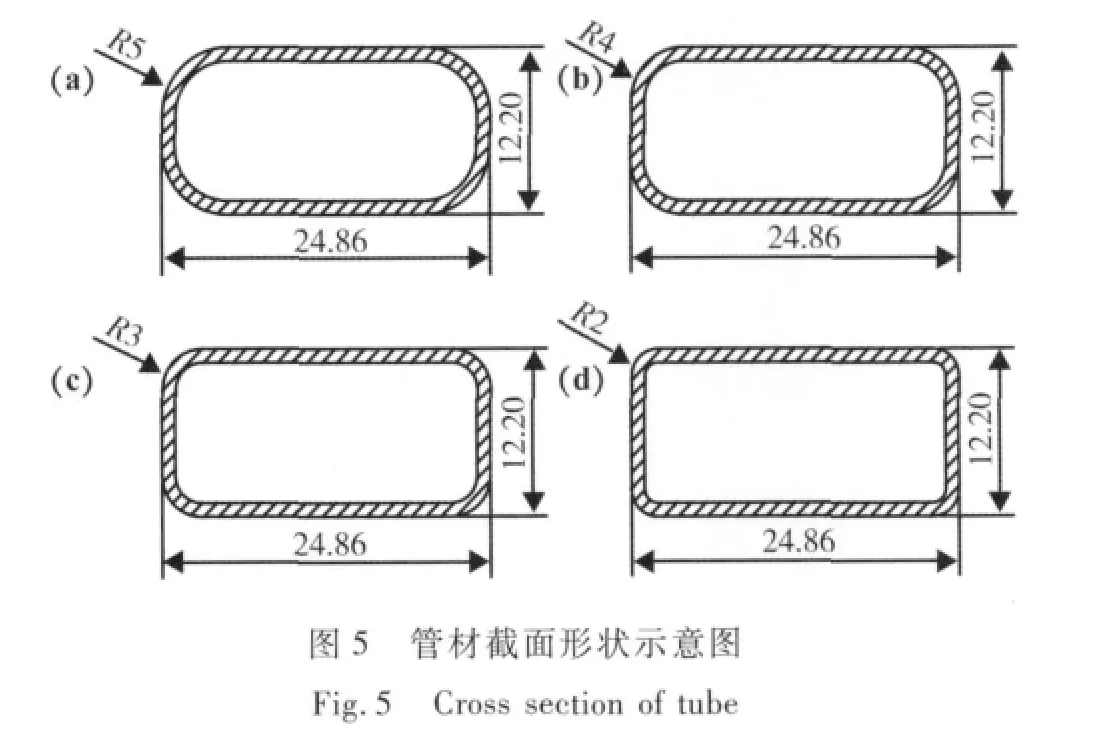
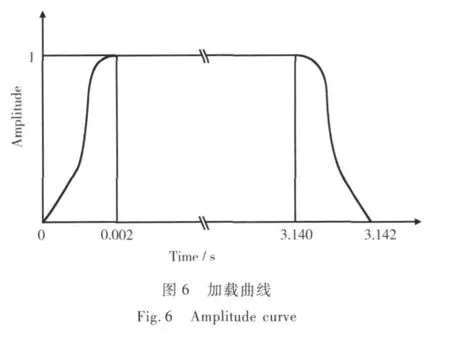
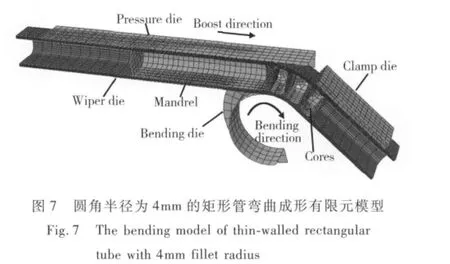
表2 带圆角的矩形管弯曲成形模拟条件Table 2 Simulation conditions of bending process

2.3 模型可靠性验证

为了验证所建模型的可靠性，根据文献［10］提供的模拟条件及材料参数，建立了外径为8mm，壁厚为0.8mm，弯曲半径为3.0 D0(D0为管材外径)的钛合金圆管弯曲过程的三维有限元模型并对弯曲过程中损伤值分布与文献中的结果进行对比，如图8所示。由图可知二者损伤值出现位置及分布区域基本一致，计算结果与文献吻合良好。为进一步验证模型的可靠性，对弯曲进程中损伤值随弯曲角度的变化规律进行了定量对比，如图9所示。从图中可知，基于本工作所建模型的模拟结果与文献模拟结果损伤值变化规律一致，随着弯曲进程的进行，损伤值急剧增加，当弯曲至60°时，损伤值达到其最大值。本工作所得损伤最大值略大于文献所得结果，二者仅相差0.013，是损伤阈值的6%，这主要是因为文献将其模拟结果与实际对比时发现其对于断裂的预测略偏保守。综上分析可知所建模型是可靠的。

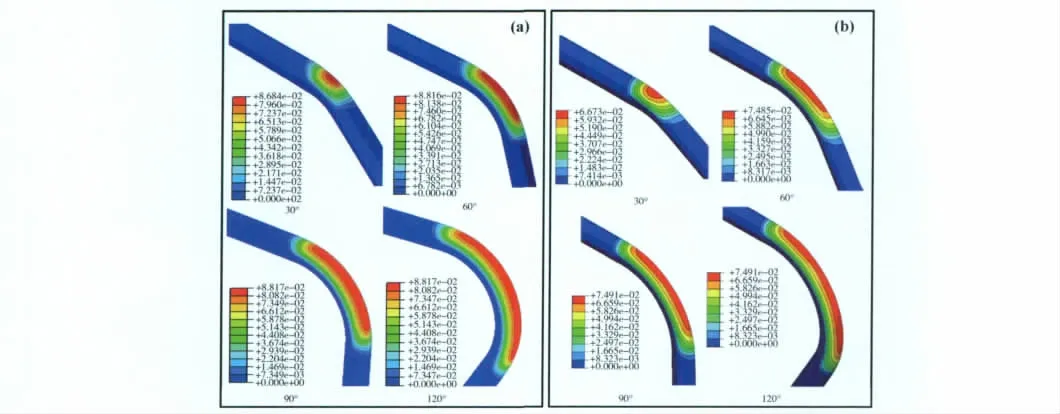
图8 所建模型模拟结果与参考文献对比图 (a)基于本工作模型所得损伤值分布云图;(b)文献［10］损伤值分布云图Fig.8 Comparisons of damage distribution (a)result obtained by presentmodel; (b)result obtained by Ref.［10］

图9 弯曲过程中损伤值变化对比图Fig.9 Comparisons of damage changing during bending process

3 壁厚与损伤值变化结果分析

3.1 壁厚变化规律研究

为了清楚的了解弯曲成形后带圆角的矩形管壁厚减薄情况，量取弯曲角为90°时，弯管弯曲段典型位置截面的壁厚变化情况，如图10所示，OC为起弯面，即弯曲开始时管材前端直线段与弯曲模的切点处，每间隔10°划分截面，量取截面位置对应的弯管对称面上外侧壁厚值t，用壁厚减薄率δ(如式(16)所示)来表示管材弯曲后的壁厚变化。

式中，t0是弯曲前的壁厚值。

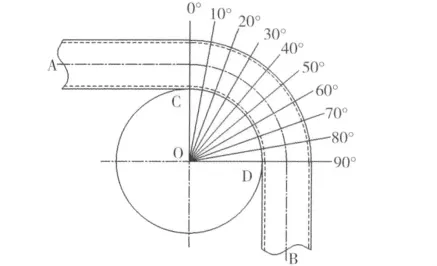
图10 测量截面位置示意图Fig.10 The sketch ofmeasured section

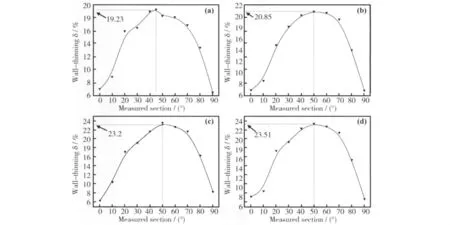
图11 不同圆角矩形管壁厚减薄率分布 (a)圆角半径为5mm; (b)圆角半径为4mm;(c)圆角半径为3mm;(d)圆角半径为2mmFig.11 Sketch of wall-thinning distribution on different fillet tube (a)5mm fillet radius;(b)4mm fillet radius; (c)3mm fillet radius;(d)2mm fillet radius

图11为采用表2所示的模拟条件得到的带有不同圆角的矩形管弯曲后壁厚减薄率分布情况。由图可知，弯曲角为90°时，截面圆角半径为5mm的矩形管壁厚减薄最大值处于45°截面处，最大壁厚减薄率为19.23%。圆角半径≤4mm的矩形管壁厚减薄率分布相似，最大值均处于50°截面处，50°截面前后壁厚呈均匀上升和下降趋势，最大壁厚减薄率分别为20.85%，23.2%和23.51%。

通过以上分析发现，带有不同圆角的矩形管壁厚减薄率最大值均出现在截面50°左右，并且随着截面圆角半径的减小壁厚减薄最大值呈增大趋势，圆角半径为2mm的矩形管壁厚减薄最严重，减薄率达到23.51%。这是因为矩形管在弯曲过程中材料受两侧板的约束作用而使其金属流动并不均匀。管材中性层外侧金属受到的流动阻力各不相同，靠近圆角处受到的流动阻力较大，处于管材外侧面中心处的流动阻力较小。在弯曲过程中，管材内侧受到挤压而壁厚增加，必然在管材截面的圆角处产生材料堆积，如图12所示。由于管材在弯曲截面40～50°变形量最大，材料堆积最严重，根据体积不变原理，此部分堆积的材料由中性层外侧的材料补偿，因此本工作所得管材壁厚减薄率最大值分布在截面50°左右。同时圆角半径越小，管材截面形状越趋于矩形化，材料流动越不均匀使材料堆积越严重，外侧壁厚减薄量也就越大。

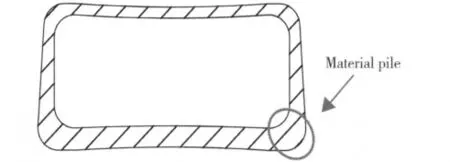
图12 矩形管截面壁厚变化引起材料堆积示意图Fig.12 Material pile of cross-section

3.2 损伤值变化规律研究

在弯曲过程中，带有不同圆角的矩形管由于其材料流动情况不同而使其损伤值分布不同，图13为带有不同圆角的矩形管弯曲完成后损伤最大值及其出现的位置。

模拟结果发现，随着圆角半径的减小，管材最大损伤值呈上升趋势。当矩形管的圆角半径为2mm时，损伤值最大为0.107，即在相对弯曲半径相同的条件下，管材截面形状越趋向于矩形越容易发生破裂。对损伤最大值出现的位置进行分析发现，各截面管材损伤最大值均出现在50°截面左右，截面圆角半径为5mm，4mm，3mm和2mm的矩形管最大损伤值分别出现在43°，54°，52°和44°截面处。从壁厚变化分析可知，四种截面的管材壁厚减薄率最大值均出现在截面50°左右，即损伤最大值与壁厚减薄率最大值出现的位置基本一致。

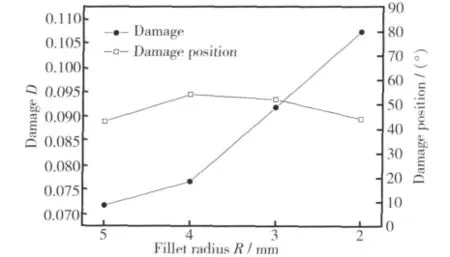
图13 最大损伤值及其位置分布图Fig.13 Maximum damage and its position of different fillet tube

对损伤形成机理进行分析可知，在材料连续形核、长大、聚集的过程中，材料内部产生微裂纹、微孔洞而发生韧性断裂。金属材料在外力作用下产生塑性变形，其内部空穴在应变和三轴应力(σH/σ-)的作用下增长、扩大，直至一定数量的空穴聚集在一起形成裂纹。在外力的继续作用下大量空穴裂纹会不断聚集在一起造成裂纹的扩展延伸，当其扩展到材料的表面时，材料就产生断裂［15］。损伤值即是对此材料内部劣化程度的量化表征。由此可见，应变和三轴应力共同影响损伤值的变化。

为了明确损伤值的变化规律与三轴应力之间的关系，取四种圆角过渡的矩形管弯曲后50°截面附近的三轴应力最大值进行分析，如图14所示，发现截面圆角半径越小，三轴应力最大值越大。由上节不同截面管材的壁厚变化情况可知，截面圆角半径越小，壁厚变化越大，即产生的厚向应变越大，因此损伤值与壁厚减薄最大值出现的位置基本一致，同时在应变与三轴应力综合作用下，管材截面圆角半径越小，损伤值越大，即管材截面越趋向于矩形，其在弯曲过程中越容易发生破裂。

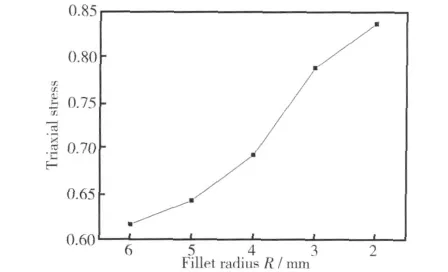
图14 不同圆角矩形管三轴应力大小Fig.14 Triaxial stress of different fillet tube

4 结论

(1)采用弹性模量变化法，通过单向拉伸反复加载卸载试验，获取了3A21铝合金薄壁矩形管的材料参数以及损伤参数，开发了耦合Lemaitre准则的用户材料子程序，建立了不同圆角的矩形管弯曲损伤预测模型，并对模型的可靠性进行了验证。

(2)不同圆角的矩形管在弯曲中，壁厚减薄分布规律基本一致，壁厚减薄最大值均出现在截面50°左右。损伤最大值与壁厚减薄率最大值出现的位置基本一致。

(3)研究发现，管材截面的圆角半径越小，其壁厚减薄越严重，损伤值越大。即在相同的相对弯曲半径条件下，管材截面越趋向于矩形，其在弯曲过程中越容易发生破裂。

［1］张津.薄壁矩形管绕弯成形截面变形和壁厚变化的研究［D］.西安:西北工业大学，2009.

［2］鄂大辛，宁汝新，唐承统，等.壁厚变形对弯管最小相对弯曲半径的影响［J］.锻压技术，2006(1):90-93. (E D X，NING R X，TANG C T，et al.Influence of wall thickness deformation upon theminimum bending radius of bending tube［J］.Forging＆Stamping Technology，2006 (1):90-93.)

［3］古涛，鄂大辛，任颖.管材弯曲壁厚变形的有限元模拟与试验分析［J］.模具工业，2009，32(4):17-20. (GU T，E D X，REN Y.Finite element simulation and experimental analysis of wall thickness deformation in the process of pipe bending［J］.Die＆ Mould Industry，2009，32(4):17-20.)

［4］岳永保.薄壁管小弯曲半径数控弯曲壁厚减薄实验研究［J］.锻压技术，2007，32(5):58-62. (YUE Y B.Experiment study on thinning of thin-walled tube NC bending process of small bending radius［J］. Forging＆Stamping Technology，2007，32(5):58-62.)

［5］王志刚，李付国，何敏.基于损伤理论的LF2M管接头胀形工艺模拟［J］.试验研究，2009(2):92-95. (WANG ZG，LIFG，HEM.Finite element simulation of bulge forming process of the LF2M anti-rust aluminum pipe coupling based on damage developmentmodel［J］.Experiment Research，2009(2):92-95.)

［6］LIH，FU MW，LU J，et al.Ductile fracture:Experimental and computations［J］.International Journal of Plasticity，2011，27(2):147-180.

［7］MKADDEM A，HAMBLIR，POTIRON A.Comparison between Gurson and Lemaitre damage models in wiping die bending process［J］.The International Journal of Advanced Manufacturing Technology，2004，23:451-461.

［8］黄婧，李立军，沈成武，等.基于连续损伤力学的金属板材成形过程损伤分析［J］.武汉理工大学学报，2006，30 (4):595-598. (HUANG J，LIL J，SHEN CW，et al.Damage analysis of sheetmetal forming for ductile fracture base on continuum damagemechanics［J］.Journal ofWuhan University of Technology，2006，30(4):595-598.)

［9］LIH，YANG H，ZHAN M.A study on critical thinning in thin-walled tube bending of Al-alloy 5052O via coupled ductile fracture criteria［C］//Proceeding of the10th NUMIFORM International Conference，2010:1286-1294.

［10］ZHAN M，GU C G，JIANG Z Q.Application of ductile fracture criteria in spin-forming and tube-bending processes［J］.Computational Materials Science，2009，47(2):353 -365.

［11］WANG Z L，LIY C，WANG JG.A method for evaluating dynamic tensile damage of rock［J］.Engineering Fracture Mechanics，2008，5:2812-2825.

［12］LEMAITRE J.A continuous damagemechanicsmodel for ductile fracture［J］.Journal of Engineering Materials and Technology，1985，107(1):83-89.

［13］SANGW，FARHANG P B.Finite element simulation of the punchless piercing processwith Lemaitre damagemodel［J］.International Journal of Mechanical Sciences，2005，47:1756-1768.

［14］赵刚要.薄壁矩形管绕弯成形起皱及成形极限研究［D］.西安:西北工业大学，2010.

［15］蒲思洪，温彤，吴维.韧性断裂准则与阀值选取的理论及试验研究［J］.金属铸锻焊技术，2009，38(3):18-21. (PU SH，WEN T，WUW.Theoretical and experimental research on choosing criterion and critical value of ductile fracture［J］.Casting·Forging·Welding，2009，38 (3):18-21.)