基于强扰动理论的蜂窝结构等效电磁模型研究
赵雨辰 万国宾
(西北工业大学电子信息学院,陕西 西安710129)
引 言
吸波材料的多功能化是国内外研究的热点之一,在军事和民用领域都有十分重要的应用价值.与早期的吸波材料相比,兼具吸波性能和承载功能的新型轻质多功能吸波结构已经成为了吸波材料研究中的主要方向[1].
蜂窝结构复合材料不仅能够较大幅度地减少材料的使用量,而且具有优良的力学与电磁学性能.这些优点使得蜂窝结构复合材料在飞行器雷达隐身设计中占有重要的地位.然而蜂窝结构本身几何结构的复杂性往往会降低雷达吸波材料多功能化设计的效率.相比于实物测试[2]和全波分析[3],一种更为方便快捷的方法是将蜂窝结构等效为一定参数的平板模型[4].这样既不需要制作多个实物进行测试,又可以避免全波分析中复杂的理论推导和数学建模,对提高多功能复合吸波材料的设计效率具有重要的意义.
国内外许多学者都对蜂窝结构的等效电磁模型进行了深入的研究.赵伯琳[5]采用介质波导理论导出了蜂窝结构吸波材料的特征方程,并指出宽频带内蜂窝结构的等效电磁参数具有色散特性.Quievy等[6]同样根据波导理论研究了填充有吸波泡沫的金属蜂窝的吸波特性.Smith[7]通过使用时域有限差分法计算了蜂窝结构的反射系数,进而提取并分析了不同情况下等效电磁参数的变化趋势.Johansson等[8]和张永杰等[9]使用有限元法得到了蜂窝结构的宏观电磁参数,并指出Hashin-Shtrikman(HS)理论可以很好地描述蜂窝结构的等效电磁参数,而且HS上下界分别适用于不同的情况.贾宝富等[10]以及何燕飞等[11]将蜂窝孔简化为横截面为圆形的纤维,采用强扰动理论推导了蜂窝结构吸波材料等效电磁参数的表达式并研究了不同结构参数时的吸波性能.总体来说,现有研究一方面表明了蜂窝结构等效电磁参数具有色散特性,另一方面也给出了诸如HS上下界等方便使用的等效模型,但却没能将两者结合起来,提出能在宽频带内描述蜂窝结构等效电磁参数色散特性的闭式数学表达式.
强扰动理论是一种解决该问题的可供选择的方法.强扰动理论开始主要用来解决颗粒混合媒质的问题[12],进而又被用来描述结构型吸波材料的等效电磁参数[10-11,13].对比两类研究可以发现,在描述结构型吸波材料的电磁参数时,以上文献都是在长波长近似下,忽略了相关项的影响,从而得到了与频率以及结构单元尺寸无关的等效电磁参数的闭式表达式,而在描述颗粒媒质的等效电磁参数时,考虑了相关项后,所得的表达式则能够反映频率以及颗粒尺寸的影响[14].
本文旨在建立宽频带内蜂窝结构的等效模型.通过建立蜂窝结构的仿真模型,在雷达工作频段2~18GHz的频率范围内采用传输反射法提取了蜂窝结构的等效电磁参数.其次对强扰动理论进行了简要的推导,通过对强扰动理论中的相关项进行修正,建立了能够描述蜂窝结构等效电磁参数色散特性的等效模型,并在不同情况下对等效模型的准确性进行了验证,且当等效电磁参数的色散特性发生变化时,采用优化算法进一步修正了强扰动理论中的相关项部分.最后对全文进行了总结.
1 蜂窝结构等效电磁参数提取
图1为蜂窝结构的示意图,蜂窝孔为正六边形,y方向的尺寸为r.单个蜂窝孔由骨架材料包围芯体材料构成,骨架的厚度为w.虚线框所示为蜂窝结构仿真模型所采用的单元结构.通过仿真计算可以得到蜂窝结构的传输反射系数,即S11和S21参数.根据传输反射法,蜂窝结构的等效电磁参数可由S参数表示为[15]
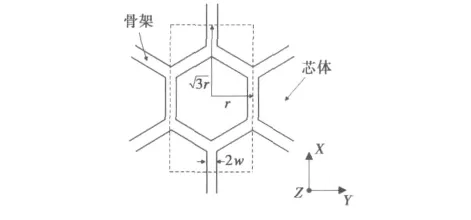
图1 蜂窝结构模型
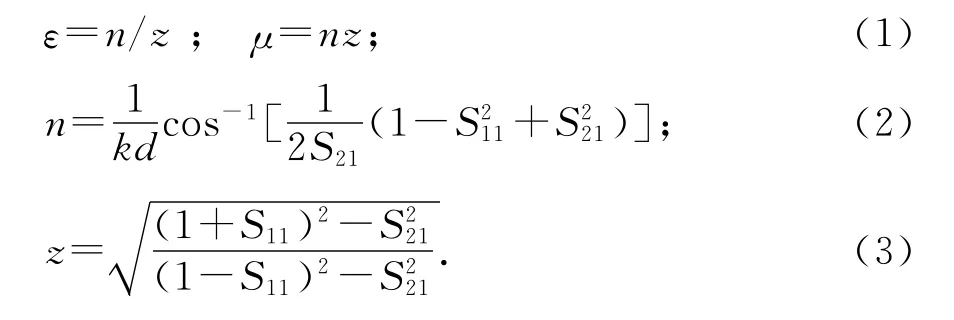
式中:d是蜂窝材料厚度;k是自由空间波数;n和z分别是蜂窝材料的折射率和波阻抗.在宽频带内使用传输反射法时,需要处理算法中的多值性[16].
在雷达工作频段内高次模均为衰减模的条件下,取骨架材料的介电常数和磁导率分别为4和1,芯体材料的介电常数和磁导率分别为12-j1和3-j1,其中j为虚数单位,并保持两种材料的占空比不变,即w=0.1r,可得蜂窝结构等效介电常数随频率以及蜂窝孔尺寸r的变化趋势,如图2所示.
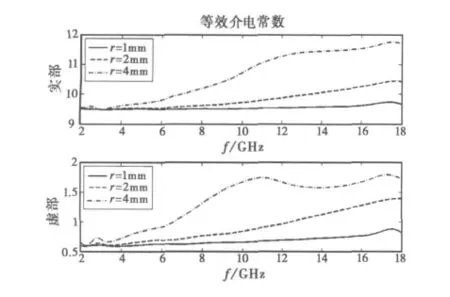
图2 r不同时等效介电常数的色散特性
从图2可知,蜂窝结构等效介电常数是具有色散特性的,并且其色散特性受到蜂窝孔尺寸的影响.等效磁导率具有相同的变化规律.由以上分析可以看出,蜂窝结构的等效模型应具备反映其等效电磁参数色散特性的能力,仅由各组分材料的电磁参数和占空比是不能够在宽频带内准确描述蜂窝结构等效电磁参数的.
2 基于强扰动理论的等效模型
根据强扰动理论,若定义随机媒质的等效本构张量为Ceq,则其表达式为[14]
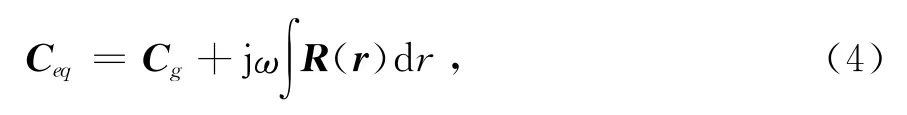
式中:R是相关项;Cg是随机媒质的静态等效本构张量.Cg可以展开为

式中:εg和μg分别表示静态介电常数张量和静态磁导率张量;Ceq也可以展开成类似的形式.
当频率为0时,即长波长极限条件下,不存在相关项的影响,则可得

上式表明,Cg代表了频率为0时随机媒质的等效本构张量.若假设混合媒质由N种成分组成,则其静态等效本构矩阵可由下式表示为
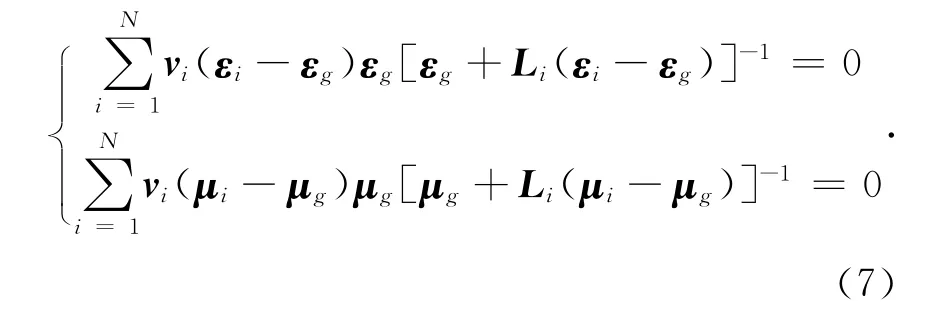
此时强扰动理论退化为Bruggman理论,即强扰动理论的零阶近似,也就是文献[10]~[11],[13]所采用的等效模型.式中εi、μi、vi、Li分别是混合媒质中第i种单质的介电常数张量、磁导率张量、占空比以及退极化张量.蜂窝孔可以等效为横截面为圆形的一致取向的纤维材料,并且由于骨架材料与芯体材料的取向一致,两者退极化张量相同.一致取向纤维的退极化张量L表示为
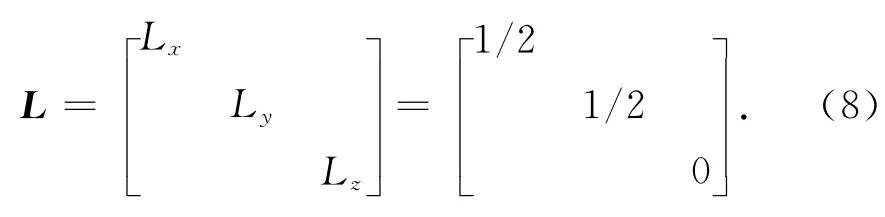
当不满足长波长极限时,相关项的影响不能忽略,而相关项反映了等效介电常数εeq与频率以及系统结构尺寸的关系[14],因此在宽频带内建立蜂窝结构等效模型的关键是计算式(4)中的积分部分,即体现相关项R影响的部分.目前并没有针对蜂窝结构等效模型中相关项部分的研究,因此,本文给出了其经验公式.参考文献[14],宽频带内蜂窝结构的等效介电常数可以表示为:
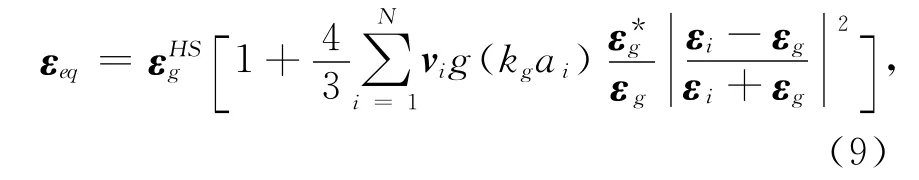
式中:等效模型在长波长极限下取HS理论的预测值,记为εHSg;*表示取共轭;g(kgai)是影响等效电磁参数色散特性的核心部分,是波数kg以及各组份材料尺寸a的函数,其一般表达式为
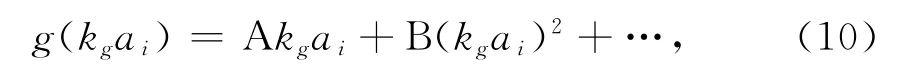
式中,A、B等为待定系数.骨架材料和芯体材料的尺寸 分别为w以及r-w.类似可得等效磁导率的表达式.
3 等效模型的验证和修正
3.1 等效模型的验证
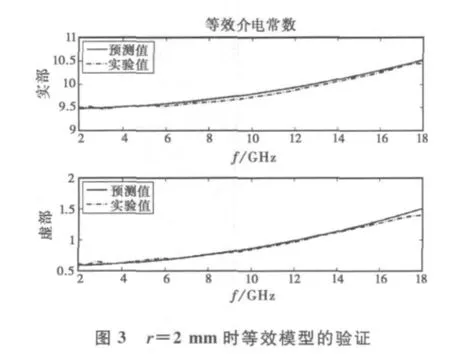
在不同情况下对所建立的等效模型进行验证.首先以图2中r=2mm,w=0.2mm的蜂窝结构为例,骨架材料的介电常数和磁导率分别为4和1,芯体材料的介电常数和磁导率分别为12-j1和3-j1,属于骨架材料电磁参数较小而芯体材料电磁参数较大的情况,经验公式中B取0.25-j0.125,其余系数为零.等效模型的效果如图3所示.
从图中可以看出,所建立的宽频带内蜂窝结构等效模型能够较为准确地描述其等效介电常数随频率的变化趋势.进而保持骨架材料和芯体材料的电磁参数和占空比不变,对r=1mm,w=0.1mm和r=4mm,w=0.4mm的情况进行验证,如图4所示.
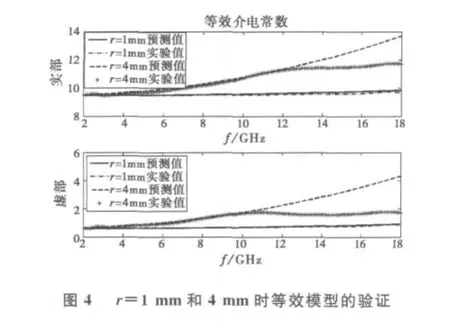
由图4可知,当蜂窝孔尺寸较小时,等效模型能够较为准确地预测蜂窝结构的等效介电常数,而当蜂窝孔尺寸较大时,在频率较低的情况下,等效模型的准确性依然较高,但当频率进一步增大时,等效介电常数随频率的变化趋势较低频时平缓,此时原等效模型已经不能准确预测蜂窝结构的等效介电常数,需要进一步对等效模型中的g(kgai)项进行修正.
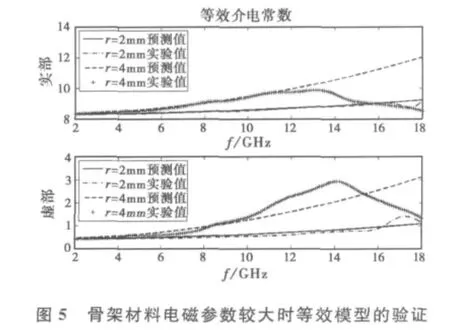
图5研究了骨架材料电磁参数较大的情况,其中蜂窝结构的单元尺寸分别取r=2mm,w=0.2mm和r=4mm,w=0.4mm,骨架材料的介电常数和磁导率分别为24-j1和3-j1,芯体材料的介电常数和磁导率分别为6-j0.2和1,经验公式中B取0.4-j0.2,其余系数为零.
图5显示等效模型在蜂窝孔尺寸较小时能够较为准确地预测蜂窝结构的等效介电常数,而当蜂窝孔尺寸较大但频率较低的情况下,等效模型能够较为准确地反映等效介电常数的色散特性,但当频率进一步增大时,预测值与实验值的偏差较大.
以上的几个算例对应于蜂窝孔内填充吸波泡沫等材料的情况,而另一种具有实际价值的例子是蜂窝壁上涂覆一层吸收剂,其结构如图6所示.
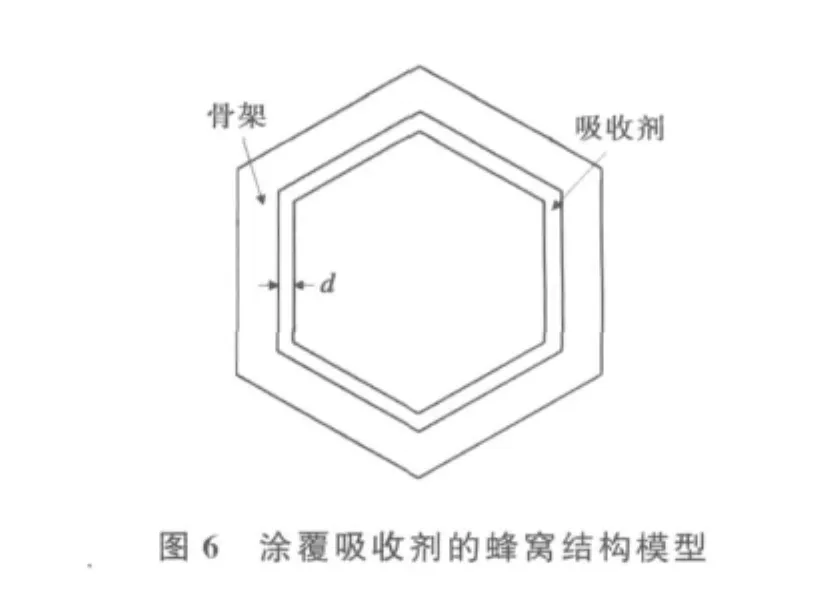
对于这种情况,计算时先使用式(9)计算由吸收层包围空气组成的较小的蜂窝结构的等效电磁参数,进而将所得到的等效电磁参数与骨架材料的电磁参数再代入式(9)即可得到整个结构的等效电磁参数[10-11].分别取r=2mm 和r=4mm,并保持w=0.1r,d=0.3(r-w)不变,骨架材料和吸收材料的电磁参数与图3实验相同,经验公式中B取0.5-j0.167,其余系数为零.等效模型的效果如图7所示.从图7中可以发现,等效模型对于涂覆型蜂窝结构是适用的,但当蜂窝孔尺寸较大且频率较高的时候,等效模型同样不能够准确描述等效介电常数随频率的变化趋势.
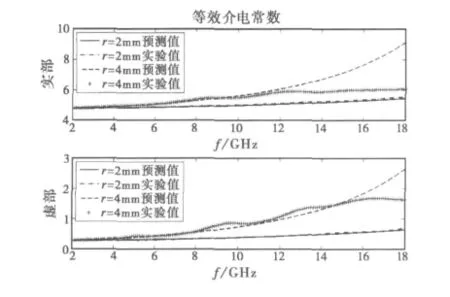
图7 涂覆型蜂窝结构的等效模型验证
3.2 相关项部分的修正
以上的验证分析一方面说明强扰动理论是建立宽频带内蜂窝结构等效电磁模型的有效方法,另一方面也显示现有相关项部分的经验公式并不足以描述所有情况下蜂窝结构等效电磁参数的色散特性,特别是当蜂窝孔尺寸较大且频率较高的时候.因此,本小节通过优化算法对相关项的修正进行了初步的讨论.以图4中r=4mm的蜂窝结构为例,g(kgai)分别取式(10)中的前三项和第二项,记为g1(kgai)和g2(kgai).在2~18GHz内选取一定数目的参考频点,定义优化算法的适应度函数为这些参考点处等效模型预测值与实验值之差的绝对值之和,进而通过运行优化算法即可得到相关项中的各个待定系数.
g1(kgai)和g2(kgai)的逼近效果如图8所示.其中,优化算法以2GHz为起点,间隔1GHz选取一个参考点,共17个参考点.运行优化算法可得g1(kgai)的待定系数分别为-0.318 7-j0.476 1、1.602 5-j0.156 9、-0.312 2+j0.008 7,g2(kgai)中的待定系数为0.631 8-j0.150 6.由图8可知,当蜂窝孔尺寸较大时,g(kgai)取更多的项等效模型的逼近效果越好,说明此时所对应的相关项的表达式更为复杂.而蜂窝结构等效电磁模型中相关项部分更一般的闭式表达式还有待进一步研究.
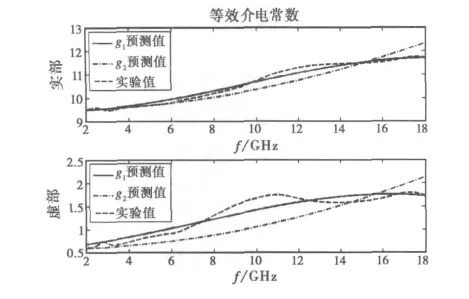
图8 g1和g2的逼近效果比较
4 结 论
本文基于强扰动理论,对宽频带内蜂窝结构的等效电磁模型进行了研究,得到以下结论:
1)强扰动理论是建立宽频带内蜂窝结构等效电磁模型的有效方法,其中的相关项是影响等效模型色散特性的核心部分;
2)当蜂窝孔尺寸较小或者蜂窝孔尺寸较大但频率较低时,本文所建立的等效模型能够较为准确地预测不同情况下蜂窝结构的等效电磁参数;
3)当蜂窝孔尺寸较大且频率较高时,蜂窝结构等效电磁参数的色散特性会发生变化,需要进一步修正强扰动理论中的相关项部分.
[1]陈明继,裴永茂,方岱宁.夹心型雷达吸波结构的多目标优化[J].应用数学和力学,2010,31(3):315-323.CHEN Mingji,PEI Yongmao,FANG Daining.Mulitobjective optimization design of radar absorbing sandwich structure[J].Applied Mathematics and Mechanics,2010,31(3):315-323.(in Chinese)
[2]HE Y F,GONG R Z,CAO H,et al.Preparation and microwave absorption properties of metal magnetic micropowder-coated honeycomb sandwich structures[J].Smart Mater Struct,2007,16(5):1501-1505.
[3]GAO Z P,LUO Q.Reflection characteristics of impregnated absorbent honeycomb under normal incidence of plane wave[J].J Electron Sci China,2003,32(4):389-394.
[4]SMITH F C,SCARPA F,CHAMBERS B.The electromagnetic properties of re-entrant dielectric honeycombs[J].IEEE Trans Microw Guided W,2000,10(11):451-453.
[5]赵伯琳.蜂窝结构吸波材料等效电磁参数的计[J].航空学报,1992,13(11):662-669.ZHAO Bolin.The calculation of effective electromagnetic parameters of honeycomb radar absorbing structural materials[J].Acta Aeronautica et Astronautica Sinica,1992,13(11):662-669.(in Chinese)
[6]QUIEVY N,BOLLEN P,THOMASSIN J M,et al.Electromagnetic Absorption properties of carbon nanotube nanocomposite foam filling honeycomb waveguide structures[J].Electromagn Compat,2012,54(1):43-51.
[7]SMITH F C.Effective permittivity of dielectric honeycombs[J].IEE Proc Microw Antennas Propag,1999,146(1):55-59.
[8]JOHANSSON M,HOLLOWAY C L,KUESTER E F.Effective electromagnetic properties of honeycomb composites,and hollow-pyramidal and alternatingwedge absorbers[J].IEEE Trans Antennas Propag,2005,53(2):728-736.
[9]张永杰,李江海,孙 秦.复合材料结构等效电磁参数均匀化方法[J].电波科学学报,2009,24(2):280-284.ZHANG Yongjie,LI Jianghai,SUN Qin.Homogenization method for effective electromagnetic properties of composites[J].Chinese Journal of Radio Science,2009,24(2):280-284.(in Chinese)
[10]贾宝富,刘述章,林为干.结构型吸波材料电磁参数的预测[J].航空学报,1990,11(9):480-486.JIA Baofu,LIU Shuzhang,Lin Weigan.The prediction of electromagnetic characteristics of structure absorbent materials[J].Acta Aeronautica et Astronautica Sinica,1990,11(9):480-486.(in Chinese)
[11]何燕飞,龚荣洲,王 鲜,等.蜂窝结构吸波材料等效电磁参数和吸波特性研究[J].物理学报,2008,57(8):5261-5266.HE Yanfei,GONG Rongzhou,WANG Xian,et al.Study on equivalent electromagnetic parameters and absorbing properties of honeycomb-structured absorbing materials[J].Acta Physica Sinica,2008,57(8):5261-5266.(in Chinese)
[12]TSANG L T,KONG J A.Scattering of electromagnetic waves from random media with strong permittivity fluctuation[J].Radio Sci,1981,16(3):303-320.
[13]PENG Z H,CAO M S,YUAN J,et al.Strong fluctuation theory for effective electromagnetic parameters of fiber fabric radar absorbing materials[J].Mater Design,2004,25(5):379-384.
[14]贾宝富.强扰动随机媒质的等效介电常数和等效磁导率[J].电波科学学报,1990,5(2):28-34.JIA Baofu.Effective Dielectric constant and permeability of strong fluctuation random medium[J].Chinese Journal of Radio Science,1990,5(2):28-34.(in Chinese)
[15]沈 静,万国宾,万 伟,等.背腔双负微带天线的仿真与实验研究[J].电波科学学报,2008,23(4):689-693.SHEN Jing,WAN Guobin,WAN Wei,etal.Simulation and experimental studies on cavity backed microstrip antennas with DNG substrates[J].Chinese Journal of Radio Science,2008,23(4):689-693.(in Chinese)
[16]胡振燕,周乐柱.一种提取介质结构等效电磁参量的改进方法[J].北京大学学报:自然科学版,2011,47(3):435-442.HU Zhenyan,ZHOU Lezhu.An improved effective electromagnetic parameters retrieval method[J].Acta Scientiarum Naturalium Universitatis Pekineneis,2011,47(3):435-442.(in Chinese)

