金属多面体上低剖面天线的矩量法分析

刘玉龙 金元松 何绍林

（中国电波传播研究所，山东 青岛266107）

引 言

现代通信环境越来越复杂，对天线的要求也越来越高，天线设计不仅要考虑增益、方向性、扫描角等电气技术指标的要求，还必须考虑天线本身的机械特性、空气动力学特性等，特别是车辆、军舰、飞机等快速移动载体上的天线更是如此.低剖面天线因其轮廓低、重量轻、风阻小及易于实现与载体共形等特点，很好地解决了上述问题.

国外早在20世纪70年代就开始了对低剖面天线的研究，国内也进行了相关的研究，如适合于飞机和舰艇的横电磁波线天线［1］，火车与站台通信的倒L型天线，适用于轿车、飞行器上的倒F天线以及广泛用于便携电话的平面倒F型天线等［2-3］.

采用矩量法分析了经典文献［4］中金属平板上的单极子天线，对细线结构、面结构及线面连接处，分别选用三种类型的三角形基函数，在面结构单元重合时采用了精确快速的奇异性处理方法［5］，并首次应用该方法进行了基于电场积分方程的阻抗矩阵推导，将计算结果与FEKO软件结果作比较，验证了方法的有效性.采用本文方法分析了金属立方体上的电小环天线.

1 理论分析

1.1 模型分解和基函数选取

对于任意形状金属导体上的线天线目标，为了使模型尽量逼近真实电流分布以及满足各连接处电流连续性，可以将导体模型分成三个部分：细线模型、表面模型和线面连接模型.对于细线模型采用直线分段，面结构采用三角形剖分.三角形面元由于其灵活性在分析任意形状物体的电磁问题时有不可替代的优越性.而对于细线模型、表面模型和线面连接模型的基函数分别选取分段三角基函数、RWG（Rao-Wilton-Gisson）矢量基函数［6］和线面连接基函数［3］，基函数的变量如图1（a）、（b）、（c）所示.

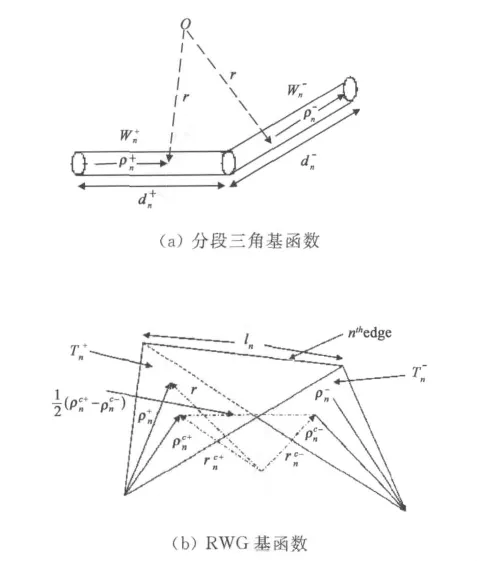
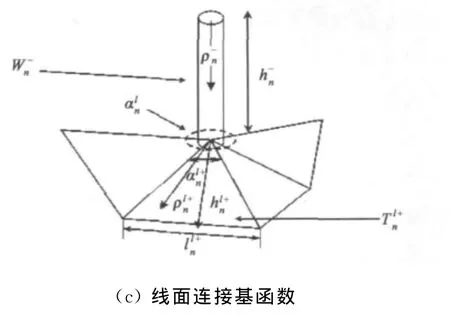
图1 基函数示意图

基函数的表达式分别为

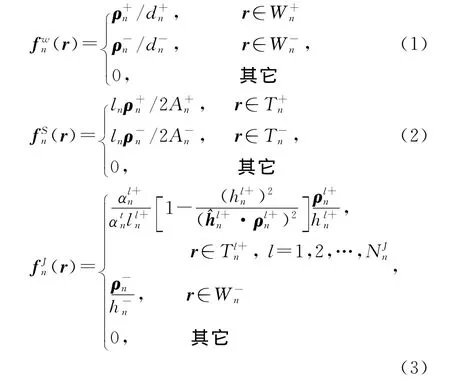
式中：W 表示细线结构；S表示面结构；J表示线面连接处.

根据上述三种模型及基函数可以得到导体面上的电流为

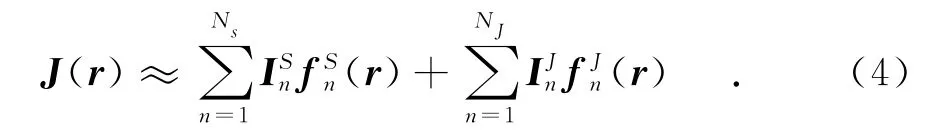
细线结构上的电流为

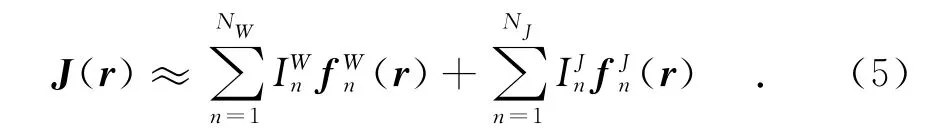
式中NS，NW，NJ分别为面结构、细线结构以及线面结合处未知电流展开系数的个数.

1.2 建立矩阵方程

将本文分析的目标看作理想导电体，对于导体表面采用电场积分方程（EFIE），

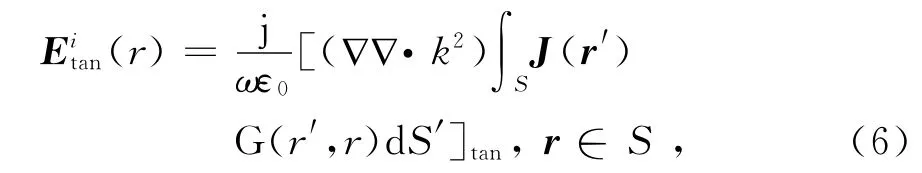
式中：下标“tan”表示切向分量；格林函数G（r′，r）＝e-jkR/4πR，R＝｜r-r′｜表示场点和源点之间的距离.对于线天线，由于是细线结构，天线上电流分布的电场积分方程可由式（6）简化得到，设沿天线方向的单位矢量为，则有

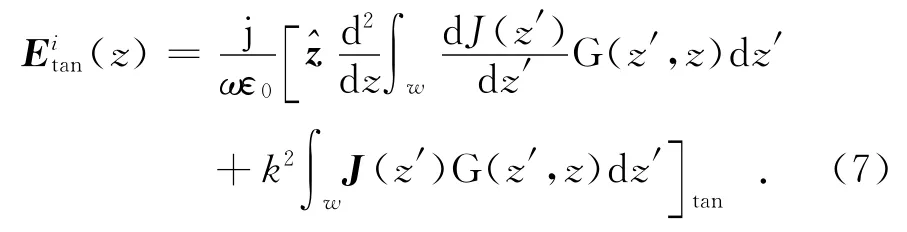
对方程（6）和（7），采用伽略金方法，即加权函数仍采用展开基函数fWn，fSn，fJn，可以得到如下矩阵方程

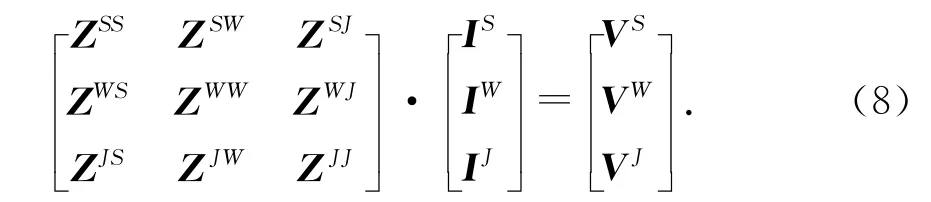
式中：Zγβ，（γ，β＝S，W，J）分别表示面结构、细线结构和线面连接处之间的相互作用及自作用矩阵；Iβ，Vβ（β＝S，W，J）分别代表不同结构模型的电流展开系数矩阵和电压矩阵.

对矩阵方程（8）的求解主要是求解阻抗矩阵元素Z，对于相互作用的矩阵元素，为简化求解过程可以采用中心近似，但自作用矩阵元素必须处理积分奇异性.以面结构为例，矩阵元素的表达式为

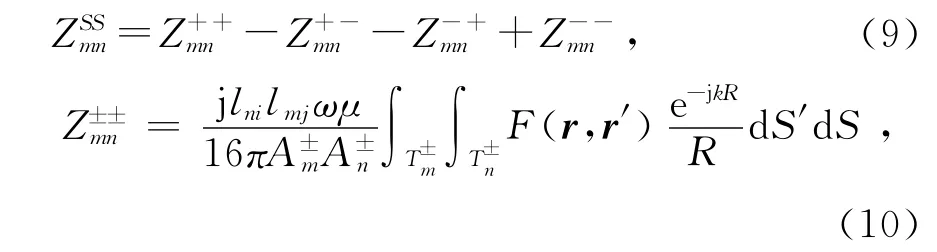
式中：F（r，r′）＝（r±′-r±ni）·（r±-r±mj）-4/k2，r′，r分别是源点和场点；A±n、A±m，rin，rmj（i，j＝1，2，3）分别为源点、场点三角形的面积和顶点；lni，lmj分别是顶点对应的公共边的边长.

1.3 积分奇异性的处理

对于细线单元的奇异性，可以将源点和场点分别选在细线的中心和表面，消除奇异性.而对于三角形面元重合时需要计算奇异性函数的两重面积分（即4维积分），该积分的计算直接影响到矩阵方程的计算效率和求解精度.对该积分的外层面积分一般采用直接数值积分法，而对应于源点的内层奇异性积分常采用奇异值提取技术［7］和Duffy坐标变换法［8-9］.奇异值提取法的奇异性积分部分具有解析结果，但非奇异性积分部分的被积函数不满足连续可导的条件，严重影响积分精度.Duffy坐标变换法具有广泛的适用性，但计算量较大.

利用参数坐标变换、相对坐标变换将奇异性积分的积分区域进行重新分区；然后利用广义Duffy坐标变换将奇异性积分转化成非奇异性积分；同时，在此过程中4维积分的某些维积分可以解析求出，降低了数值积分的积分维数，提高了数值积分效率和计算精度.

当场源三角形单元重合时，将场源三角形的空间坐标分别用面积坐标（ξ1，ξ2），（η1，η2）表示后，交换ξ2和η1的积分次序并引入相对坐标（u1，u2）变换

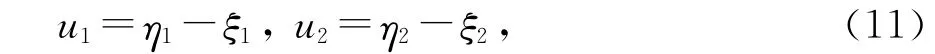
可以将原4维积分式（10）（以三角形面元重合时的Z＋＋nn为例并简记为Z）拆为6个4维的分区域积分，

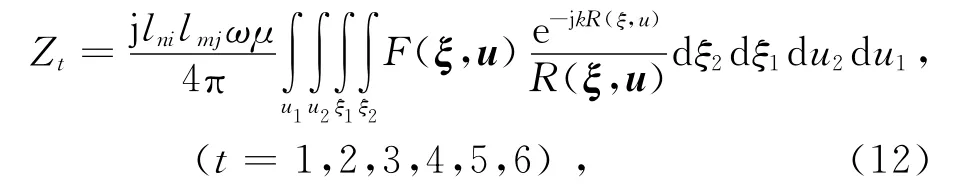
式中：ξ＝（ξ1，ξ2）、u＝（u1，u2），6个4维积分的积分区间划分见文献［5］.

利用式（11）可将场源之间的距离R表示为

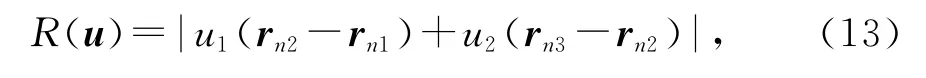
式（13）表明，距离R仅是相对坐标u的函数，与面积坐标ξ无关.由于对u积分区域的对称性可以将式（12）的6个积分合并成为3个积分［5］：

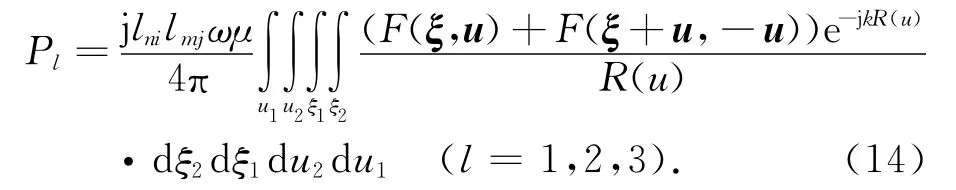
对于平面三角形单元上的RWG矢量基函数，式（14）中的F（ξ，u）和F（ξ＋u，-u）总是ξ的二次多项式，且距离R与ξ无关，因此，式（14）中关于ξ的积分可解析求出，并表示为

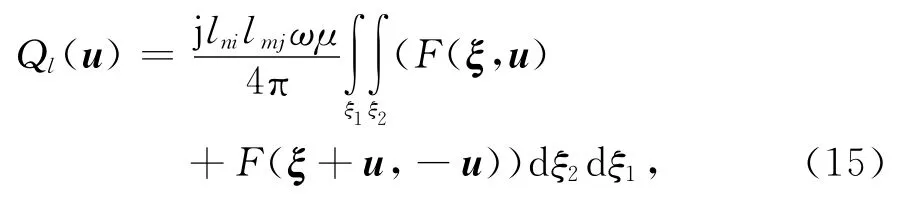
对式（15）的外两层积分作广义Duffy坐标变换［5］，可将每个积分Pl均转换为非奇异性积分：

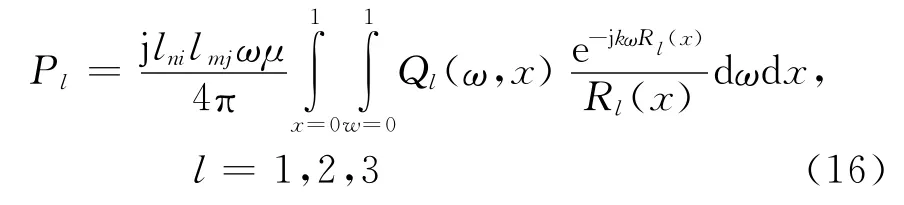
三角形面元重合时的自阻抗矩阵元素为

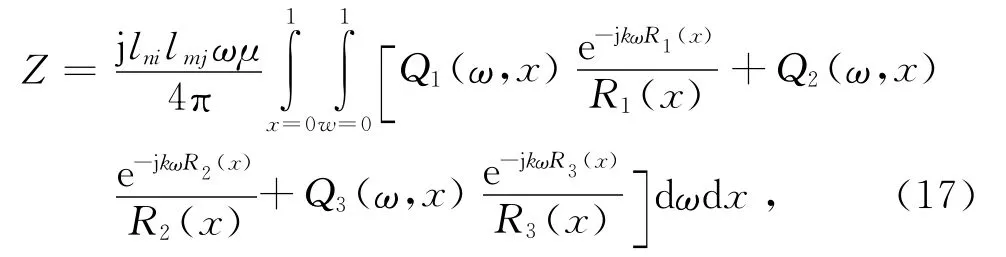
式中：场源之间的距离R为

式中：

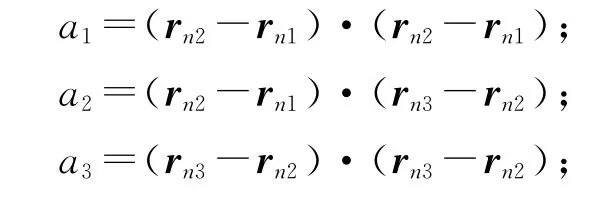
（rn1，rn2，rn3）为场源三角形单元的三个公共结点坐标 .从式（18）可以看出积分区域内无论取何值总有R（x）≠0，因此含有奇异性的积分式（12）就转换成了非奇异性积分.经过复杂的积分运算可以求出式（17）中Ql（ω，x）的解析表达式：

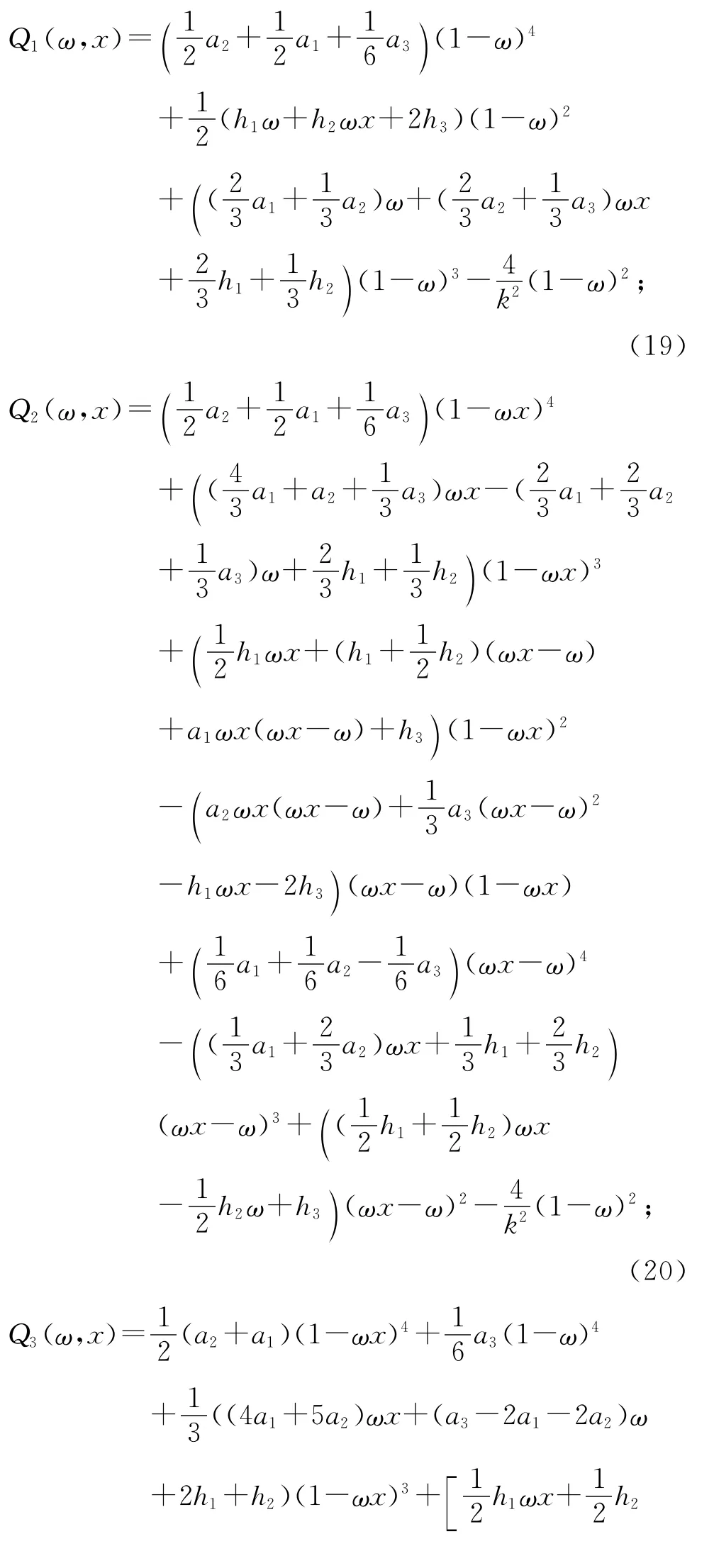
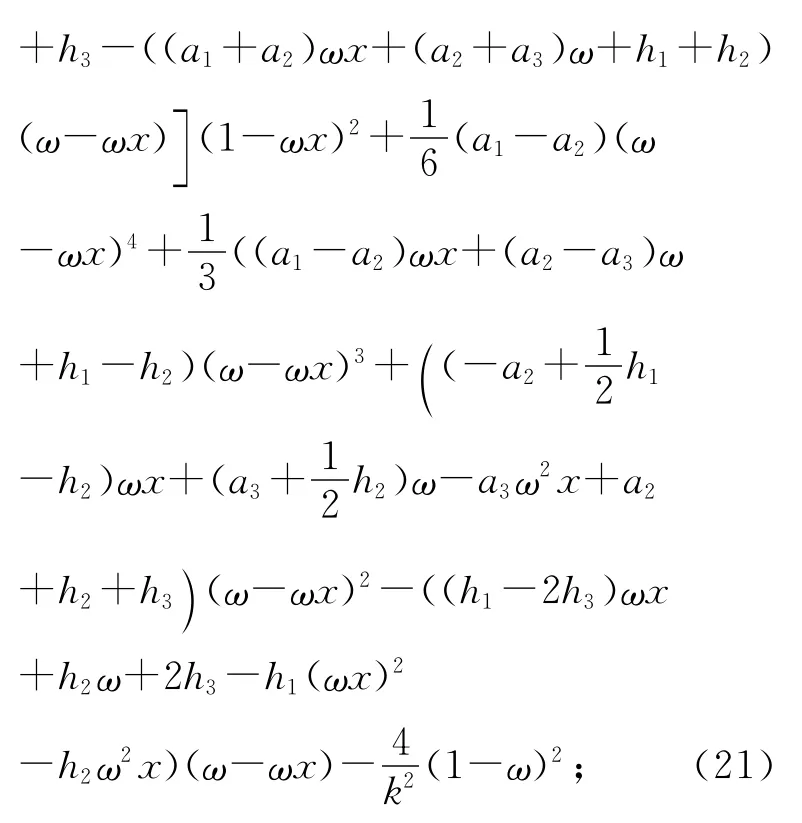
式中：

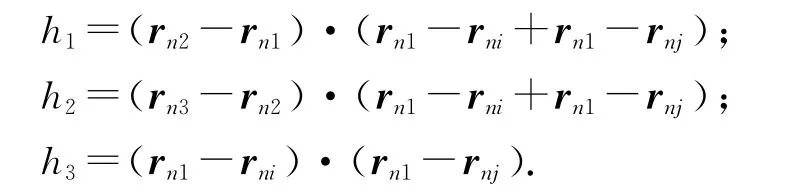
i，j＝1，2，3，i与j的取值由三角形面上RWG矢量基函数的方向决定.

由于式（17）的被积函数总是可以写成ω的多项式和e-jkωRl（x）相乘的形式，ω 的积分可以解析的求出，从而式（17）也可进一步化成相关的一维数值积分.由于化简过程更加繁琐，本文直接用二维数值积分.

2 数值结果

首先选择经典文献［4］中平板及单极天线的尺寸，平板0.914m×0.914m，单极天线高度0.421 m，线径0.008m，频率范围140～200MHz，馈电在线面连接处采用δ电压源，各频率点的输入阻抗如图2所示.

从图2可以看出，本文方法与FEKO软件计算结果吻合很好，证明了本文公式推导及计算方法的正确性.

采用本文方法分析金属立方体上不同位置的低剖面电小环天线，如图3所示.

线高度0.3m，宽度0.8m，线径0.01m；立方体边长8m×8m×8m.天线馈电端为a1，负载端为b1，在位置1、位置2及位置3处的坐标分别为a1（4.4，4，8），b1（3.6，4，8）a2（4.4，5.6，8），b2（3.6，5.6，8），a3（4.4，7.2，8），b3（3.6，7.2，8）.频率为 30 MHz时，环天线在三个不同位置的输入阻抗如表1所示，远场区总场辐射方向图如图4所示.

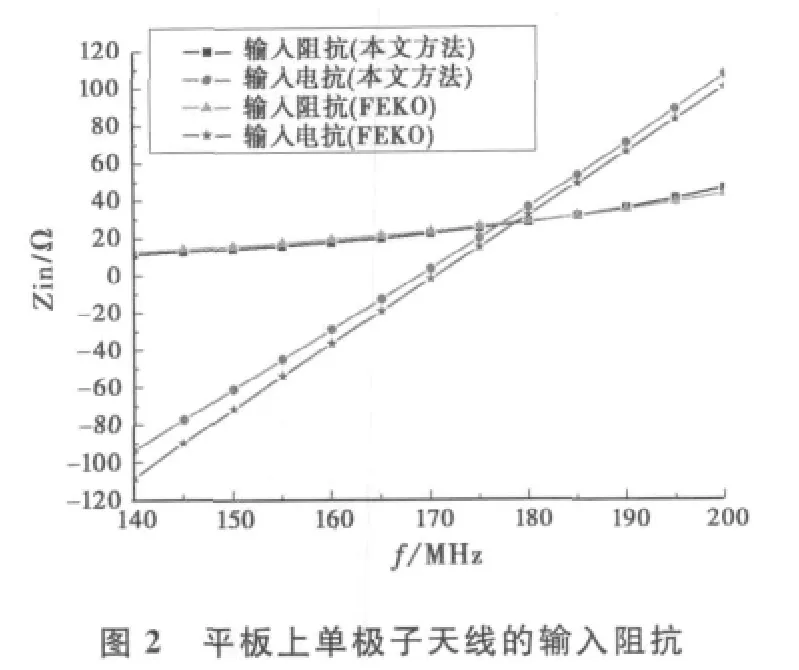
表1 金属立方体上环天线的输入阻抗

由表1及图4可以看出：电小环天线的阻抗特性随位置变化不敏感，并且通过调节可以获得较好的心形辐射.因此，在对电特性影响较小的情况下可以将环放在金属载体的不同位置，这对在有限空间上（如车辆顶部、军舰舰体两侧、飞机两翼）设计低剖面天线或天线阵提供了有利条件.

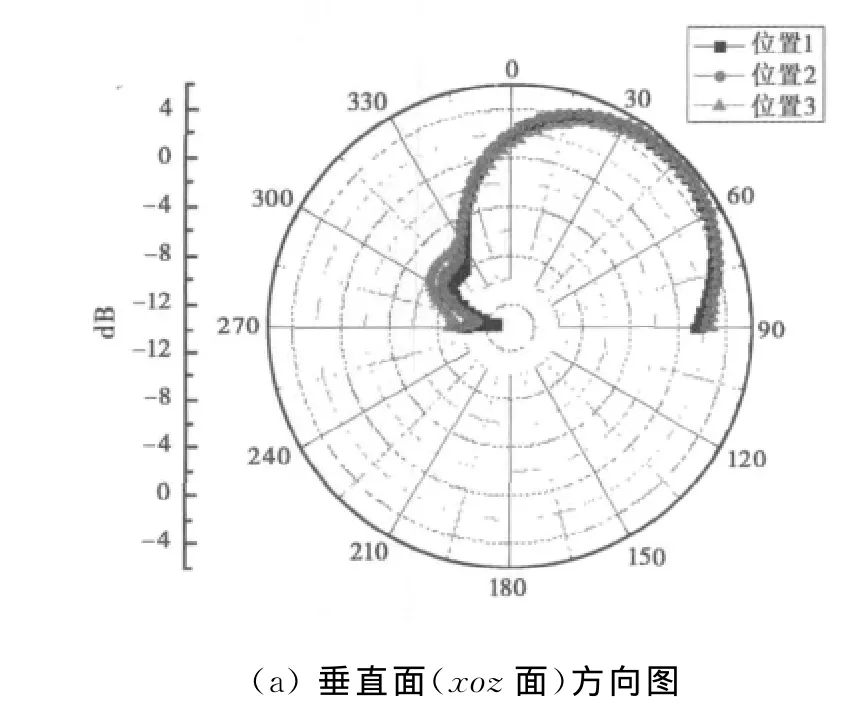
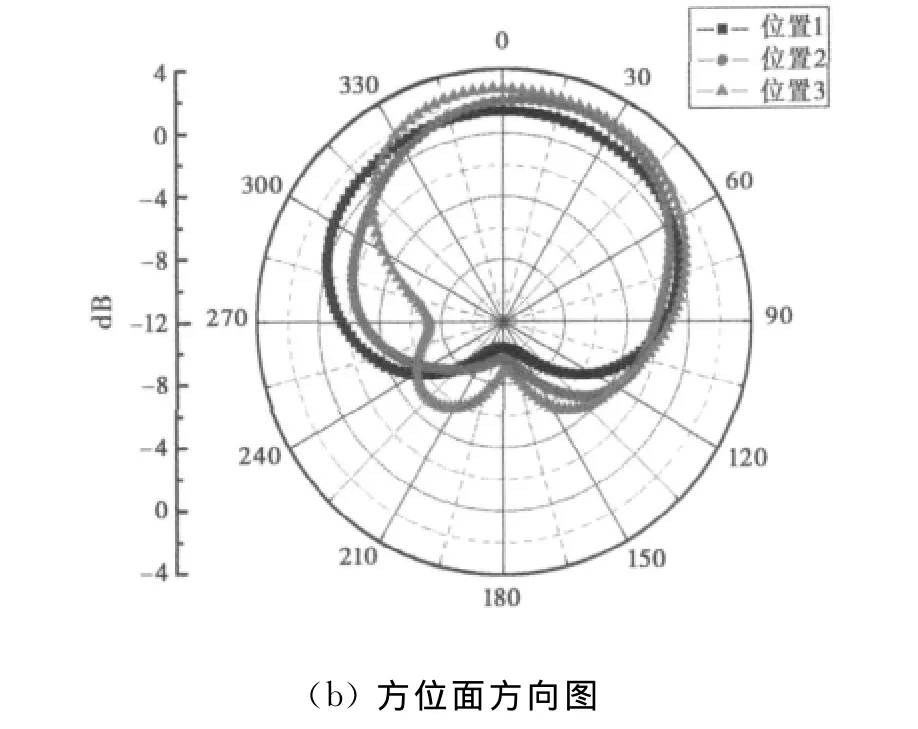
图4 金属立方体上低剖面电小环天线的方向图

3 结 论

采用矩量法将任意导体上的低剖面天线进行整体分析，并首次对文献［5］的精确快速算法进行了完整的公式推导及应用.虽然，文中是以金属立方体上的单副电小环天线为例进行分析，但方法本身适用于任意形状金属导体上低剖面天线或天线阵的分析与设计.

［1］MITTRA R.Computer Techniques for Electromagnetics［M］.Oxford：Pergainon Press，1973.

［2］秦 益.飞行器载低剖面倒F天线特性分析［J］.遥测遥控，2004，25（5）：35-43.QING Yi.Characteristics of inverse F antenna onboard aircraft［J］.Telemetry ＆ Telecontrol，2004，25（5）：35-43.（in Chinese）

［3］SATO K，MATSUMOTO K，FUJIMOTO K，et al.Characteristics of planar inverted-F antenna on a rectangular conducting body［J］.Trans IECIE，1988，J71-B：1237-1243.

［4］HWU S U，WILTON D R.Electromagnetic Scattering and Radiation by Arbitrary Configurations of Conducting Bodies and Wires［R］.Houston：University of Houston，1987.

［5］赵延文，聂在平，徐建华，等.基于RWG基函数的伽略金法中奇异性积分的精确快速计算［J］.电子学报，2005，33（6）：1019-1023.ZHAO Yanwen，NIE Zaiping，XU Jianhua，et al.Accurate and efficient calculation of singular integrals in Galerkin method with RWG basis functions［J］.Acta Electronica Sinica，2005，33（6）：1019-1023.（in Chinese）

［6］RAO S M，WILTON D R，GLISSON A W.Electromagnetic scattering by surfaces of arbitrary shape［J］.IEEE Trans Antennas and Propagat，1982，30（3）：409-418.

［7］GRAGLIA R D.On the numerical integration of the linear shape functions times the 3-D Green’s function or its gradient on a plane triangle［J］.IEEE Trans Antenna and Propagat，1993，41（10）：1448-1455.

［8］DUFFY M G.Quadrature over a pyramid or cube of integrands with a singularity at a vertex［J］.SIAM J Numer Anal，1982，19（6）：1260-1262.

［9］CHEW W C，JIN J M，MICHIELESSEN E，et al.Fast and Efficient Algorithms in Computational Electromagnetics［M］.Boston：Artech House，2001.