双基地多入多出雷达收发方位角联合估计算法

陈显舟 杨 源 韩静静 李立萍

（1.中国电子科技集团公司第十研究所，四川 成都610036；2.中国人民解放军93975部队，新疆 乌鲁木齐830005；3.电子科技大学电子工程学院，四川 成都611731）

引 言

为了适应现代信息化战争的需要，与传统相控阵雷达相比，在目标探测、杂波抑制、抗干扰、低截获、目标参数估计精度、目标识别等方面具有明显优势的多入多出（Multiple Input Multiple Output，MIMO）雷达的概念和相应的信号处理技术日益受到科研工作者的广泛关注.传统双基地雷达在反隐身、抗干扰、抗反辐射导弹等方面极具优势，但是时间、角度、频率（相位）如何同步技术上很难实现.将MIMO技术引入到双基雷达中，在无需角度同步先决条件下，实现二维收发方位角的同时测量，回避了双基雷达“角度同步”难题，双基MIMO雷达集合前两种技术优势于一身，发展前景极为广阔.

小阵元间距收发天线分置的双基MIMO雷达，通过多个发射天线同时向外辐射一组正交信号，利用波形分集和接收端多通道相干处理，增加了系统的自由度和可检测目标数目，角度空间分辨率和参数的估计性能也进一步得到提高.针对此种双基MIMO雷达高精度目标定位方法，文献［1］和［2］分别提出了基于二维多重信号分类（Multiple Signal Classification，MUSIC）和Capon谱峰搜索的收发方位角的联合估计算法，但是二维谱峰搜索运算负担极为繁重，且运算复杂度和估计精度均与搜索的步长有关，不便于实际应用.为了降低运算复杂度，文献［3］将旋转不变子空间（Estimating signal parameters viarotational invariance techniques，ESPRIT）算法［4-5］同时应用到发射端和接收端，利用信号子空间的旋转不变性，来估计目标的发射和接收方位角，但需要额外的角度配对.文献［6］在文献［3］的基础上，根据两次ESPRIT的关系，避免了目标的二维方位角参数配对过程，但仍需要两次样本协方差矩阵估计及特征分解过程，算法的运算复杂度仍不容小觑.文献［7］利用 MIMO雷达形成的虚拟阵列数据来构造两个二阶统计量并对其进行联合对角化得到了目标方位角和俯仰角的闭式解.该方法解决了存在一维角度兼并时目标的二维波达方向（Direction of Arrival，DOA）估计问题，且无需二维谱峰搜索和参数配对.但该方法阵列孔径损失较大，尤其是当接收阵元数较少时，将出现较大的角度估计偏差.文献［8］基于MIMO雷达虚拟阵元孔径扩展效应，在发射端配置两个或三个天线，在接收端虚拟出发射阵元，从而可以在接收端利用DOA矩阵方法同时估计目标的去波方向（Direction of Departure，DOD）和DOA，在多目标情形下，利用此方法得到的二维收发方位角由于特征值和特征向量的一一对应特性能够自动配对.但是，该方法没有充分利用接收端的虚拟发射阵元效应来改善DOD和DOA的角估计性能，阵元利用率不高，且有效角度估计范围较小.文献［10］通过解耦合处理，将二维的收发方位角分离为两个一维方位角估计过程，采用两次多项式求根分别进行估计，避免了二维谱峰搜索，极大降低了计算量，且无需额外的配对算法，最大可定位数目不少于接收阵元数目.不足之处是该方法仅利用了特征值信息，没有联合利用特征矢量信息，角估计性能有进一步提升的空间.

在文献［8］构造的双发射天线小间距双基MIMO雷达模型基础之上，提出了一种基于多项式求根理论的DOD和DOA联合估计算法.所提方法相对于文献［8］方法，最多可检测目标数目翻番，空间角分辨率更高，有效测角范围更加宽广，稳健性更好，运算复杂度相对于文献［8］方法略微增加，但以此代价换取性能的极大改善是值得的.所提方法相对于文献［8］和［10］方法，在低信噪比或短采样数据情形下角估计性能更好.最后，通过多次相互独立的蒙特卡洛实验验证了所提算法的有效性和实用性.

1 数据模型

考虑如图1所示的双基MIMO雷达系统，发射和接收布置成小天线间距均匀线阵，其中发射和接收天线数分别为M，N，天线间距分别为dt，dr.假定空域存在P 个目标，其中（φp，θp），（p＝1，2，…，P）为目标相对于发射和接收阵列的方位角.设定雷达工作在窄带远场平面波条件下，且接收和发射位于同一相位中心，M个发射阵元同时向外辐射一组相互正交的重复周期相位编码信号，满足＝1，2，…，M 且i≠j，si和sj分别表示第i和j个阵元发射的信号矢量，L为在每个重复周期内的相位编码个数，也即一个脉冲内的码长.假定在每个重复周期内目标的雷达散射截面积（Radar Cross-Section，RCS）保持不变，而在不同重复周期之间目标的RCS是独立变化的，并且不同目标的RCS波动是不相关的.发射和接收导向矢量分别记作at（φ）＝，相应的目标反射系数分别为α1，α2，…，αP，由于不同目标的反射系数及路径损耗不同，假定αP服从均值为0、方差为σ2p的复高斯分布.则接收阵列的回波信号表示为［9-10］

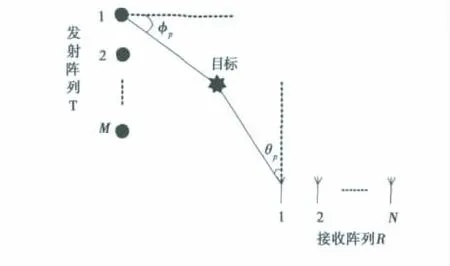
图1 双基MIMO雷达系统示意图

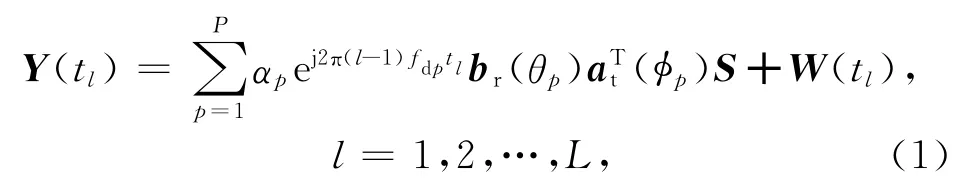
式中：fdp＝（vtp＋vrp）/（λfr）表示第p 个目标的归一化多普勒频率，vtp和vrp分别表示第p个目标相对于发射和接收阵列的径向速度，fr为脉冲重复频率，λ为载波波长；S＝［s1… sM］T；W 为均值为0、方差为σ2w的加性复高斯白噪声矢量，且与信号部分相互独立.利用M个发射信号分别对每个接收阵元接收的Q个脉冲的回波信号进行匹配滤波，将匹配后的接收信号写成矩阵形式，可表示为

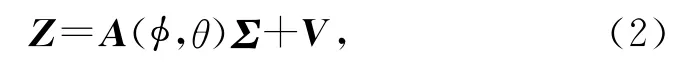
式中：Z＝［Z1…ZQ］∈CMN×Q，Zq∈CMN×1，q＝1，2，…，Q，表示第q个发射脉冲时回波信号通过相关接收机组得到的 MN×1维矢量；A（φ，θ）＝At（φ）□Ar（θ）＝［at（φ1）⊗br（θ1）… at（φP）⊗br（θP）］，□ 和 ⊗分别指代Khatri-Rao乘积和Kronecker直积，αpq（p＝1，2，…P；q＝1，2，…，Q）为第p个目标在第q个发射脉冲扫描时的目标反射系数.由式（2）可知，接收阵列可等效为阵元数为MN的虚拟阵列，其输出数据的快拍数为Q.

2 所出算法描述

假设发射端包含两个发射阵元，即M＝2，则由式（2）可得第一、二个发射阵元对应的接收信号矩阵分别为

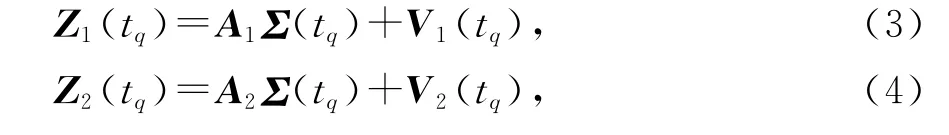
式中：A1＝Ar（θ）；A2＝A1D，D＝diag；V1和V2为加性高斯白噪声矢量.

链接阵列输出数据Z1，Z2，有

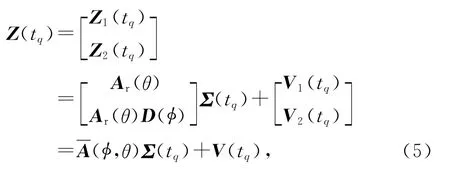
式中：

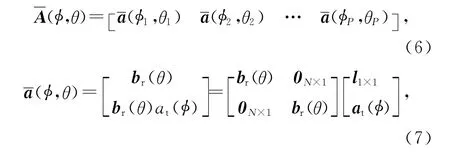
为扩展导向矢量.

由以上假设可得，扩展阵列协方差矩阵为

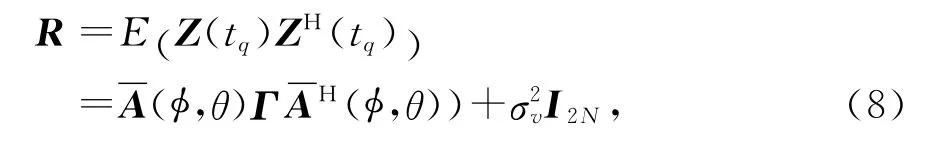
式中：Γ＝E （Σ（tq）ΣH（tq））为P×P维非奇异矩阵；σv2＝（1/L）σ2w；E（·）为对随机变量取期望操作符；（·）H表示复共轭转置.

对R进行特征分解，可得

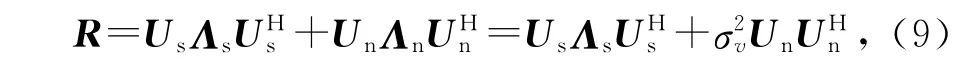
R的P个大特征值Λs＝diag（λ1λ2… λP）对应的特征矢量张成信号子空间，（2 N-P）个小特征值Λn＝diag（λP＋1λP＋2… λ2N）对应的特征矢量张成噪声子空间，两者相互正交.二维收发方位角估计通过最小化式（10）可得，且有

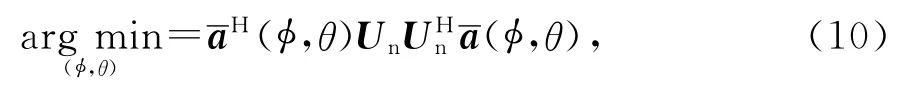
整个伪谱峰值搜索在一个二维平面内展开，运算复杂度极高，难以适应实时测向系统.

依据式（7）和（10）的代价方程可改写为如下形式：

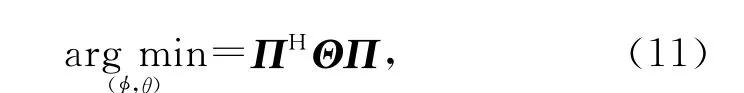
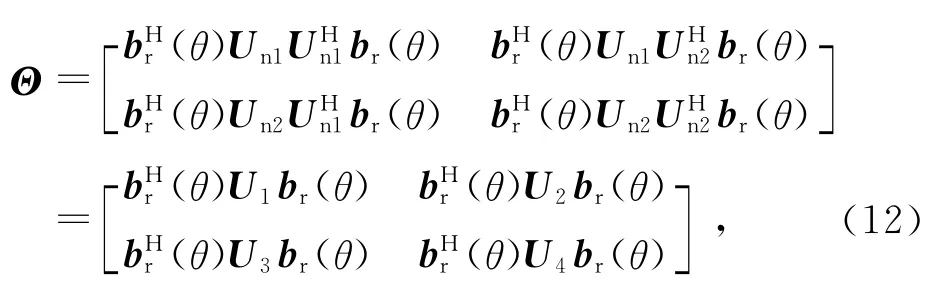
式中，子阵Un1和Un2维数相同，

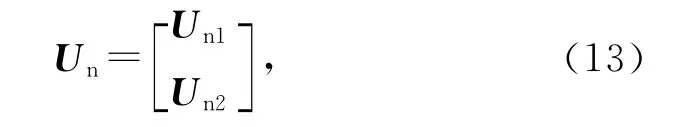
且U1＝Un1UHn1，U2＝Un1UHn2，U3＝Un2UHn1，U4＝Un2UHn2.

通过如上的解耦合处理，使得二维最小化问题变成两个相互独立的一维最小化问题，大大降低了运算量，便于实时处理.

令

br（θ）可改写为

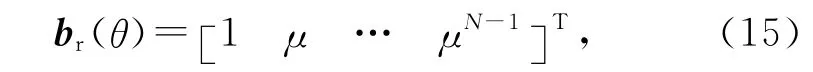
此时，矩阵Θ 为μ 的方程.θp，p＝1，2，…，P，可通过求解μ的如下等式获得

θp的估计问题就转换成一个多项式求根问题，可以通过计算高效的求根算法得到其解.

μ的多项式可以表示为如下形式

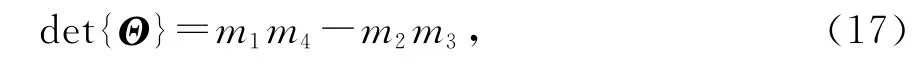
式中：

因而，mk为μ的多项式，其第i个系数由Uk（k＝1，2，3，4）的第i条对角线的和得到，其中i＝-N＋1为下对角线，i＝N-1为上对角线.设uk＝［uk，1… uk，i… uk，2N-1］T表示多项式mk系数的列向量，有

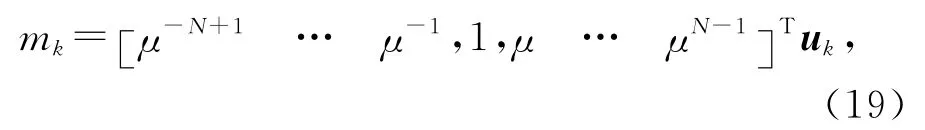
式中：

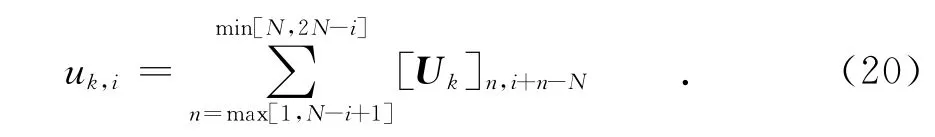
可以得到如下关系式为

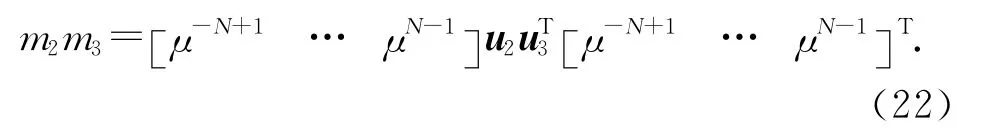
因此，多项式m1m4和m2m3的系数分别等于矩阵u1u4T和u2u3T的反对角元素的和 .令gq＝［gq，1… gq，f… gq，4N-3］T为包含4N-3个系数的列向量，

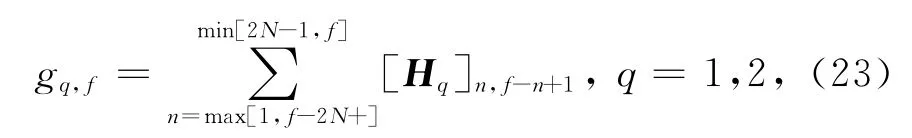
式中：H1＝u1uT4；H2＝u2uT3.则可以得到

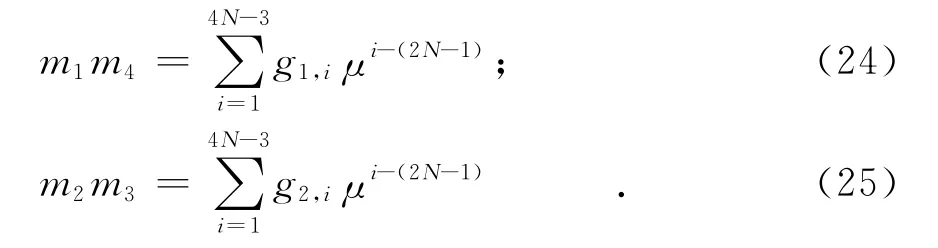
由此式（16）可以改写为

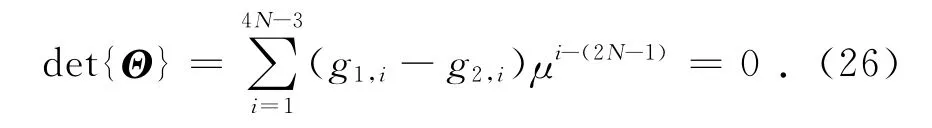
式（26）的根可以通过高效的多项式求根算法得到.θp，p＝1，2，…，P，可通过求解如下等式获得：

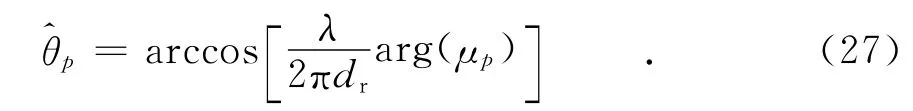
同时，φp，p＝1，2，…，P，由p对应的最小特征值的特征矢量得到，即

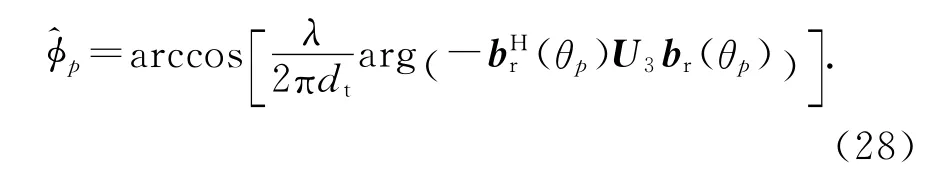
μp表示多项式用于求解p的一个根 .根据多项式系数的对称性，我们可以选择P个最靠近单位圆的不等根作为μp的估计值.

多项式det｛Θ｝的自由度为4 N-4，包含4 N-3个系数.因此，根的总数为4 N-4，由于其根成对出现，所提方法最多可以估计2（N-1）个信号源的二维收发方位角，约为文献［8］方法的两倍，所提算法的空间角分辨率更高，在低信噪比或短采样数据情形下角估计性能更好，有效测角范围更加宽广，稳健性更好.由于特征值和特征矢量存在一一对应关系，所估得的二维收发方位角能够自动配对，不需要额外的配对算法.

3 运算复杂度分析

所提算法需要如下几个步骤：①依据式（5），链接接收阵列匹配滤波后的数据矩阵Z1，Z2；②求取链接后阵列数据的样本协方差矩阵，并对其作特征分解，获得信号和噪声子空间；③对得到的噪声子空间按照式（13）进行划分，得到子阵Un1和Un2，进而求得Uk，k＝1，2，3，4；④由Uk（k＝1，2，3，4）的各条对角线元素之和，依据式（20），求得多项式mk（k＝1，2，3，4）系数列矢量uk；⑤依据式（21），（22）求得多项式m1m4，m2m3的系数列矢量，据此求得多项式（26）的根，反解式（27）获得收方位角估值p，p＝1，2，…，P；⑥得到p对应的最小特征值的特征矢量，反解式（28）即可获得发方位角估值p，p＝1，2，…，P.

通常情况下，为了获得阵列协方差矩阵的有效估计，阵列接收数据的快拍数Q远大于阵列接收阵元数目，即Q≫N.估计样本协方差矩阵的运算量约为N2Q，对一个N×N维的矩阵进行特征分解需要的运算量约为O（N3）.文献［8］和［10］算法的运算复杂度约为2 N2Q＋O（N3），所提算法的运算复杂度约为（2 N）2Q＋O（2 N）3.所提算法运算复杂度相对于文献［8］和［10］方法略微增加，但以此代价换取性能的极大改善是值得的.

4 仿真实验

为了验证所提算法的有效性，本小节特给出仿真实验加以验证.

双基地MIMO雷达系统结构如图1所示，假设发射和接收阵列均为阵元间距为半波长的均匀线阵，即dt＝dr＝λ/2.在发射端，两个阵元发射相互正交的Hardmard码波形，即M＝2，接收阵元数目N＝7，接收端脉冲回波信号数目为Q＝1 000.

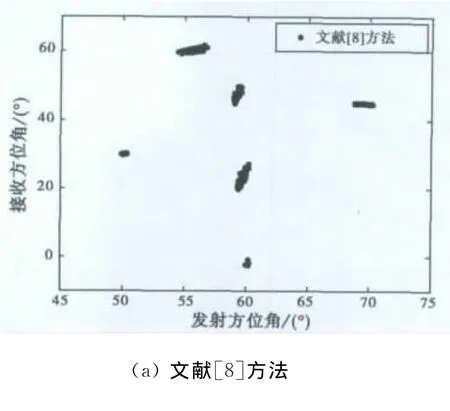
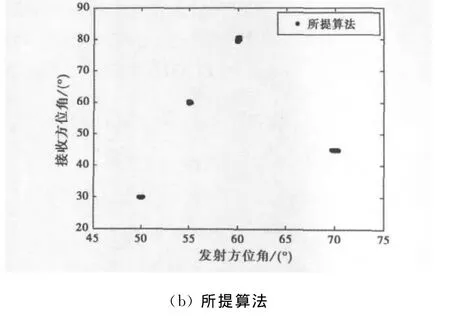
图2 目标二维收发方位角估计星座图

实验1：假设空域目标数目P＝4，分别位于DOD＝［50°，55°，60°，70°］，DOA＝［30°，60°，80°，45°］.在信噪比RSN＝0dB条件下，做200次相互独立的蒙特卡洛实验，图2分别给出了文献［8］方法和所提算法对目标二维收发方位角进行定位所得的星座图.从实验1可以看出：文献［8］方法可检测信源数目极其有限，当空域目标数P＞（N-1）/2时，其估计目标二维收发方位角的误差较大，导致对目标的定位偏离了真实位置，出现了错误位置的虚拟目标.所提算法由于产生了虚拟阵元效应，使得算法可检测信源数目成倍增长，能够对空域多个目标的二维收发方位角度进行准确估计，并能自动配对，可实现对多目标的有效测向.

实验2：假设空域目标数目P＝1，在信噪比RSN＝0dB条件下，φ，θ的步长值为2.65°.做100次相互独立的蒙特卡洛实验，图3分别给出了文献［8］方法和所提算法在整个空域内的测向性能曲线图.

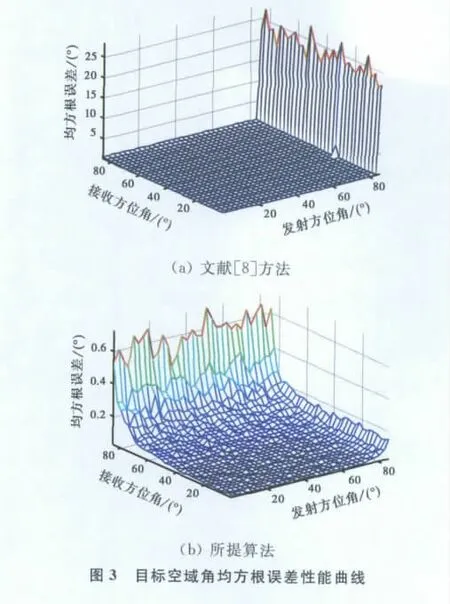
从实验2可以看出：所提算法在整个观测区域内的估计精度小于0.7°，估计性能远远优于文献［8］方法.文献［8］方法在发方位角φ＝90°附近时，估计精度大于25°，估计性能大大下降完全失效.所提算法在整个待测空间内的空间角均方根误差基本均匀，有效测角范围更加宽广，稳健性更好，所提算法适合对较大的观测区域内实现全方位测向.

实验3：假设空域目标数目P＝2，分别位于DOD＝［50°，60°］，DOA＝［75°，85°］.信噪比 SNR在0～20dB之间变化时，做10 000次相互独立的蒙特卡洛实验，图4给出了文献［8］、文献［10］方法和所提算法对空域两个目标的二维收发方位角估计的联合均方根误差（root mean squared error，RMSE）随信噪比变化性能曲线图，RMSE定义如下

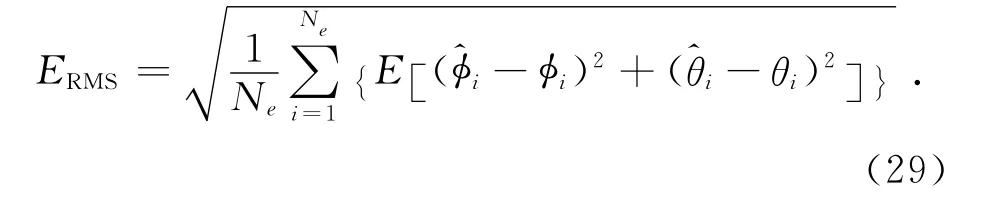
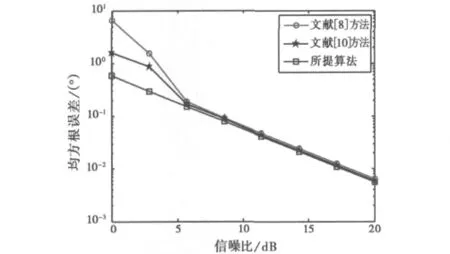
图4 收发方位角联合均方根误差随信噪比变化曲线

实验4：假设空域目标数目P＝2，分别位于DOD＝［50°，60°］，DOA＝［75°，85°］.信噪比 RSN＝0dB，快拍数在800～2 000之间变化时做10 000次相互独立的蒙特卡洛实验，图5给出了文献［8］、文献［10］方法和所提算法对空域两个目标的二维收发方位角估计的联合均方根误差随快拍数变化性能曲线图.

从实验3、4可以看出：所提算法由于产生了虚拟阵元效应，扩展了有效阵列孔径，算法的空间角分辨率更高，角估计性能更为优良.尤其在低信噪比和短采样数据情形下，所提算法相对于文献［8］和文献［10］方法性能改善明显，特别是信噪比在0～3dB之间时，文献［8］方法基本失效，而所提算法依然有效，且角估计精度很好.

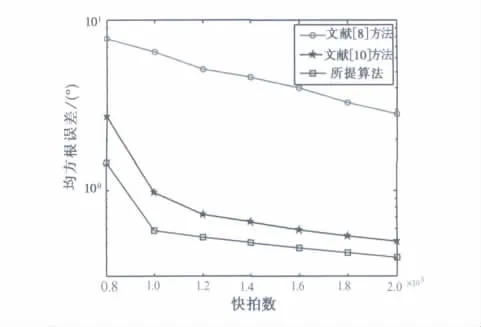
图5 收发方位角联合均方根误差随快拍数变化曲线

5 结 论

针对小天线间距收发分置的双基地MIMO雷达，基于多项式求根理论，提出了一种高精度二维收发方位角联合估计算法.所提算法充分利用MIMO雷达虚拟阵元效应，提高了空域可检测目标数目；同时阵列孔径得到扩展，改善了低信噪比或短采样数据情形下角度估计性能，扩宽了有效测角范围，算法的鲁棒性更好.所提方法无需二维伪谱峰值搜索，所估得的二维收发方位角能够自动配对.因此，所提算法的实用价值很高，适合对较大的观测区域内实现全方位高精度测向.

［1］LI J，CONAN J，PIERRE S.Joint estimation of channel parameters for MIMO communication systems［C］∥Second International Symposium on Wireless Communication Systems，5-7September，2005：22-26.

［2］YAN H，LI J，LIAO G.Multitarget identification and localization using bistatic MIMO radar systems［J］.EURASIP Journal on Advances in Signal Processing，2008，8（2）：1-8.

［3］CHEN D，CHEN B，QI G.Angle estimation using ESPRIT in MIMO radar［J］.IEE Electronics Letters，2008，44（12）：770-771.

［4］ROY R，PAULRAJ A，KAILATH T.ESPRIT-a subspace rotation approach to estimation of parameters of cisoids in noise［J］.IEEE Trans ASSP，1986，34（5）：1340-1344.

［5］ROY R，KAILATH T.ESPRIT-estimation of signal parameters via rotational invariance techniques［J］.IEEE Trans ASSP，1989，37（7）：984-995.

［6］CHEN J，GU H，SU W.Angle estimation using ESPRIT without pairing in MIMO radar［J］.IEE Elec-tronics Letters，2008，44（24）：1422-1423.

［7］郭艺夺，张永顺，童宁宁，等.一种 MIMO雷达二维DOA估计新方法［J］.电波科学学报，2010，25（4）：668-673.GUO Yiduo，ZHANG Yongshun，TONG Ningning，et al.A novel method of 2-D DOA estimation for MIMO radar［J］.Chinese Journal Of Radio Science，2010，25（4）：668-673.（in Chinese）

［8］JIN M，LIAO G，LI J.Joint DOD and DOA estimation for bistatic MIMO radar［J］.Signal Processing.，2009，89（2）：244-251.

［9］刘晓莉，廖桂生.基于 MUSIC和ESPRIT的双基地MIMO雷达角度估计算法［J］.电子与信息学报，2010，32（9）：2179-2183.LIU Xiaoli，LIAO Guisheng.Combined MUSIC with ESPRIT algorithm for angle estimation in bistatic MIM0radar system［J］.Journal of Electronics＆Information Technology，2010，32（9）：2179-2183.（in Chinese）

［10］谢 荣，刘 峥.基于多项式求根的双基地 MIMO雷达多目标定位方法［J］.电子与信息学报，2010，32（9）：2197-2200.XIE Rong，LIU Zheng.Multi-target localization based on polynomial rooting for bistatic MIMO radar［J］.Journal of Electronics＆Information Technology，2010，32（9）：2197-2200.（in Chinese）