垂直入射空变等离子体光子晶体带隙特性研究

杨利霞 陈 伟 孔 娃 施卫东 于萍萍

（1.江苏大学通信工程系，江苏 镇江212013；2.江苏大学 流体机械工程技术研究中心，江苏 镇江212013）

引 言

光子晶体是指具有光子带隙（PBG）特性的人造周期性电介质结构，有时也称为PBG光子晶体结构.所谓的光子带隙是指某一频率范围的波不能在此周期性结构中传播，即这种结构本身存在“禁带”.从材料结构上看，光子晶体是一类在光学尺度上具有周期性介电结构的人工设计和制造的晶体.20世纪80年代 Yablonovitch［1］，John［2］等提出了光子晶体的概念.光子晶体的研究近年来不断深入并且作为一个新兴研究的方向深受国内外的关注［3］.目前，无论是民用方面还是军事方面，无论是学术界还是工业界，都激起了人们极大的热情.人们利用光子晶体的这个特性在发光二极管、光纤、光集成器件等方面有广泛的运用［4-9］.

等离子体光子晶体（PPC）是由等离子体和介质交替排列的一种人工周期性结构，它的概念是由Hojo等［10］提出.它涉及等离子体物理学、电磁学、电子学、固体物理学、材料学等诸多学科，属于交叉学科范畴.等离子体光子晶体的研究近年来取得了突飞猛进的发展.短短几年中，各国学者已经投入其大量精力进行相关研究，同时大量的相关文献不断得以涌现.等离子体光子晶体的特性主要包括：光子带隙特性、光子局域特性和光学特性.其中光子的带隙特性尤为引起人们的关注，在光学上，人们利用等离子体光子晶体的特性可以制造微波滤波器、等离子体天线，文献［10-14］仅对在不考虑外磁场和等离子体层为均匀分布的等离子体光子晶体进行了研究，然而在实际应用过程中等离子体频率也会随着空间位置的变化而发生变化.对非均匀等离子体频率情况下的研究，能找到的文献并不是很多，国际上，O.Sakai，T.Sakaguchi和 K.Tachibana［15］等对非均匀等离子光子晶体做了一些相关研究.目前国内也处于起步阶段，有南昌大学的刘崧和南京航空航天大学的刘少斌等［16］，对非均匀分布等离子体光子晶体光子的带隙分析做了相关研究，其主要是基于由密度线性分布、非磁化、碰撞、中温的等离子体和电介质构成的一维等离子体光子晶体的光子带隙特性.以上就是等离子体光子晶体国内外的一些相关情况.因此，研究等离子体频率的空间变化对等离子体光子晶体禁带的影响，在工程应用方面具有重要的理论意义.

针对等离子体光子晶体频率的空间变化进行了研究，采用改进的磁化等离子体时域有限差分（FDTD）方法讨论了等离子体频率随空间呈脉冲函数形式变化的等离子体光子晶体带隙特性.通过计算电磁波的反射系数和透射系数获得其禁带结构.在一维情况下计算了垂直入射的情形，通过改变等离子体频率的大小来验证空变等离子体光子晶体的带隙特性.

1 空变等离子体光子晶体的FDTD迭代式

在各向异性色散介质碰撞磁化等离子体中，Maxwell方程组和相关的本构方程为

式中：ε0为真空中的介电常数；μ0为真空中导磁率；ωp（z）是关于空间变化的函数；ωb＝eB0/me为电子旋转频率，B0为外部静态磁场，e和me各自表示电子电量和电子质量.

对于一维情况下的横电磁波（TEM波），并设外磁场的方向为＋z方向即ωb＝ωb，在笛卡尔坐标下的各矢量表示为

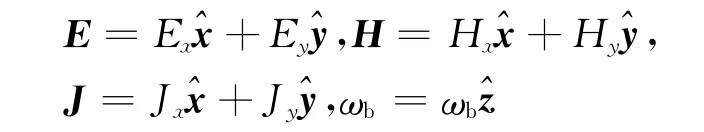
在上述坐标下，则有（1）和（2）两式可写为如下形式

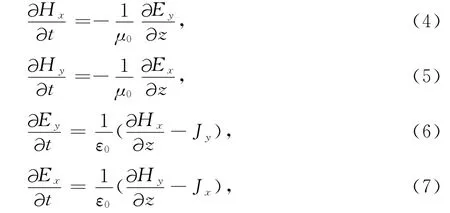
将式（3）改写为矩阵可得

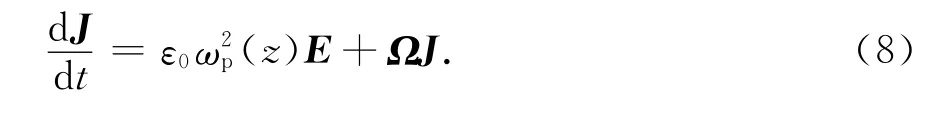
式中：

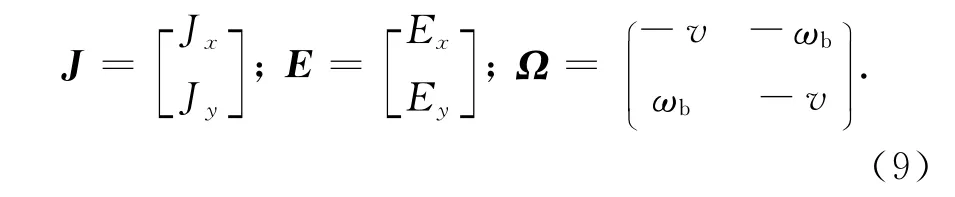
对公式（8）利用如下拉普拉斯变换对进行拉普拉斯变化得［17］

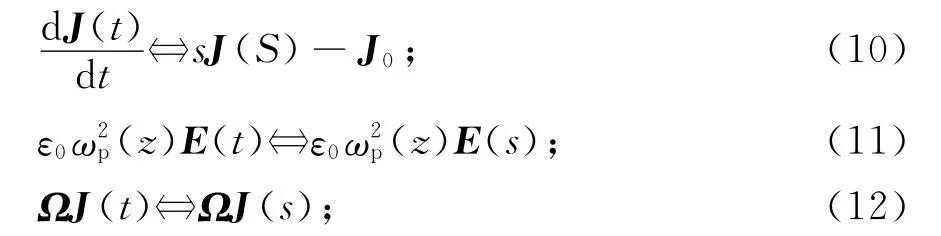
整理可得

式中：

再对式（13）逆拉普拉斯变换可得

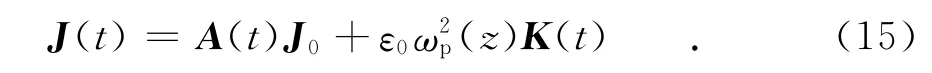
式中

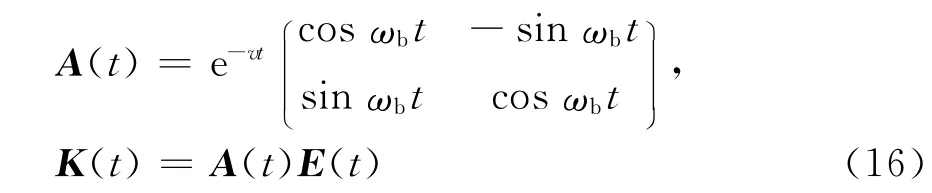
先对式（15）在时间上进行离散可得

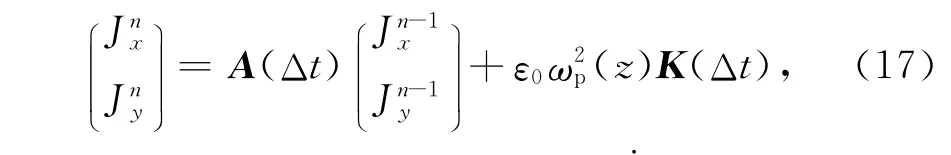
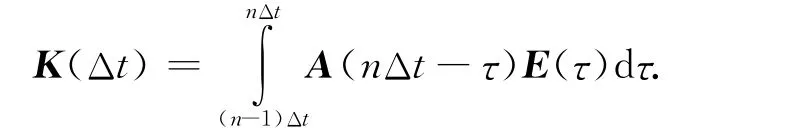
这里在n时刻对J（t）进行离散后，由式（4）和式（5）知磁场的迭代方程为

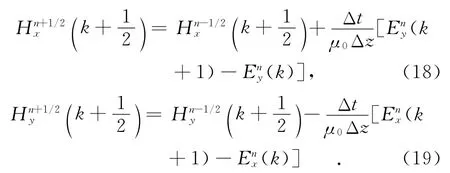
由式（6）和式（7）知电场的迭代方程为

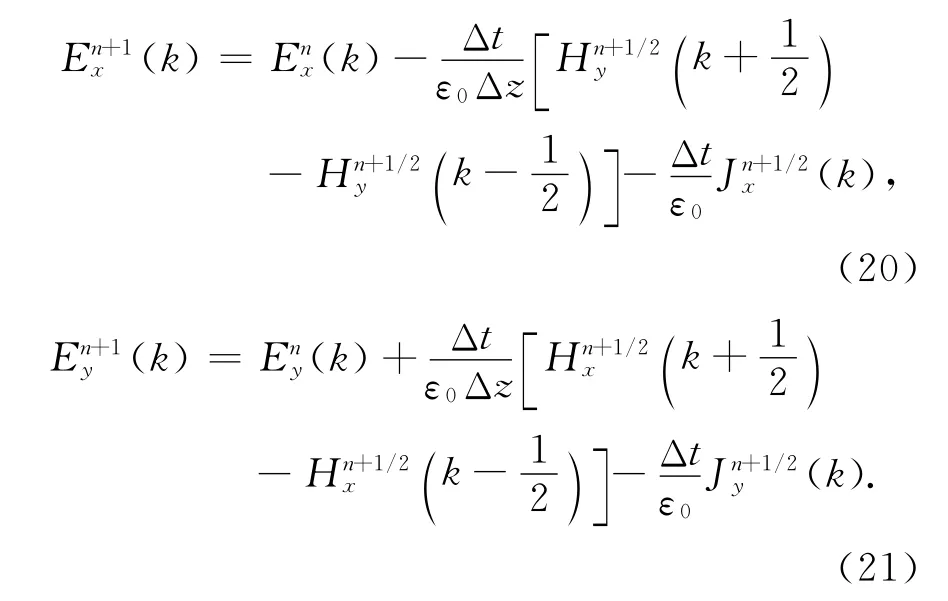
2 ωp（z）的空变函数关系式及其图形

ωp（z）在空间位置的取值随着函数z的变化而不同，这里ωp（z）为高斯脉冲形式的周期函数［18］为

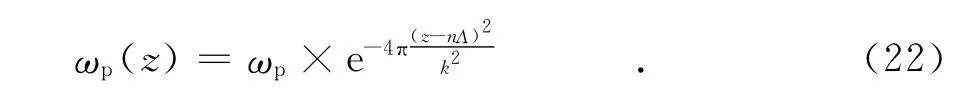
式中：k是高斯脉冲函数的宽度，k越大等离子体频率变化越缓，k越小等离子体频率变化越迅速；Λ为等离子体介质和普通介质的总宽度；n为介质板层数.ωp（z）的空变函数关系式图形如图1所示.

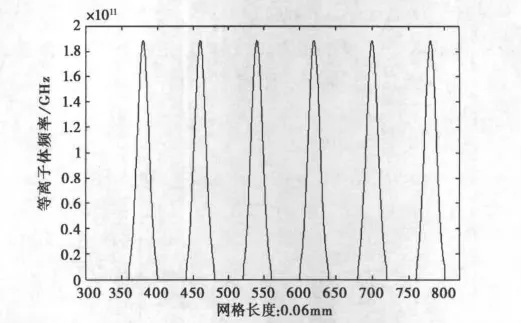
图1 等离子体频率ωp（z）

3 算例验证

利用改进的空变等离子体光子晶体的FDTD算法并选用均匀等离子体频率所得反射系数与非空变（均匀）等离子体光子晶体的反射系数进行算例验证，模型为7层介质、6层等离子体构成的等离子体光子晶体.等离子体频率设为ωp＝2π×109rad/s，实际物理结构如图3所示，图中a为普通介质宽度，b为等离子体介质宽度.计算时，a＝b＝2.4mm，FDTD的空间步长为60μm，时间步长为0.02ps.两端采用Mur吸收边界，入射波为微分高斯脉冲.计算结果如图2所示.

从图2可以看出数值解和理论解的结果完美一致，验证了空变等离子体算法的准确性.

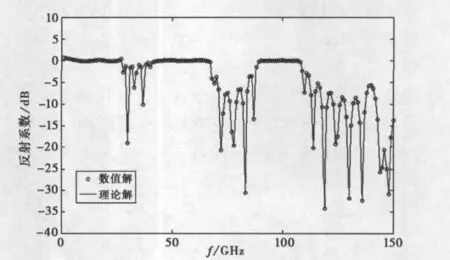
图2 一维垂直入射验证算例

4 空变等离子体光子晶体的带隙特性分析

4.1 空变等离子光子晶体的模型及参数

空变等离子体光子晶体（PPC）的物理模型同验证算例，如图3所示.电磁波垂直入射到该一维等离子体光子晶体结构.中间层状空变等离子体的等离子体频率变化规律如式（22）所示.计算中，入射波波形为微分高斯脉冲即E（t）＝-4.67 ·，其中t0＝22×10-12s，τ＝5.4×10-12s，FDTD的计算参数空间步长Δz＝60×10-6m，时间步长Δr＝1.0×10-14s.

图3 等离子光子晶体图

4.2 非磁化等离子体情形

对于空变非磁化（ωb＝0）等离子体，计算中ωp＝2π×109rad/s，碰撞频率v＝0，分别计算了脉冲宽度k＝0.6mm、1.2mm、2.4mm与均匀等离子体频率的反射系数与透射系数，计算结果如图4，图5所示.

图4、图5给出的是空变情况与非空变情况下PPC的反射系数和透射系数频谱图，从图中可以清楚的看到：无论是反射系数还是透射系数，空变等离子体频率的反射系数和均匀介质反射系数有非常大的差别，等离子体光子晶体的禁带随着高斯脉冲函数宽度k的变化而有规律的变化，随着k的逐渐变小光子晶体的禁带中心频率也逐渐向低频方向移动，但光子晶体的周期性并没有改变.这说明通过改变ωp（z）的高斯脉冲形式的函数宽度对PPC结构的禁带形成是可控的.

图4 非磁化情况下空变PPC与非空变PPC反射系数图

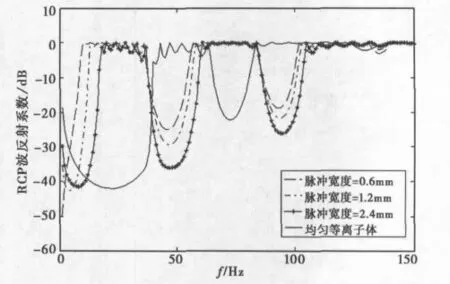
图5 非磁化情况下空变PPC与非空变PPC透射系数图

4.3 磁化等离子体情形

对于磁化（ωb＝10GHz）等离子体情形，计算中，ωp＝2π×10GHz，碰撞频率v＝10GHz，分别计算了脉冲宽度k＝0.6mm、1.2mm、2.4mm 与均匀等离子体频率的反射系数与透射系数频谱对比图，如图6、图7所示.

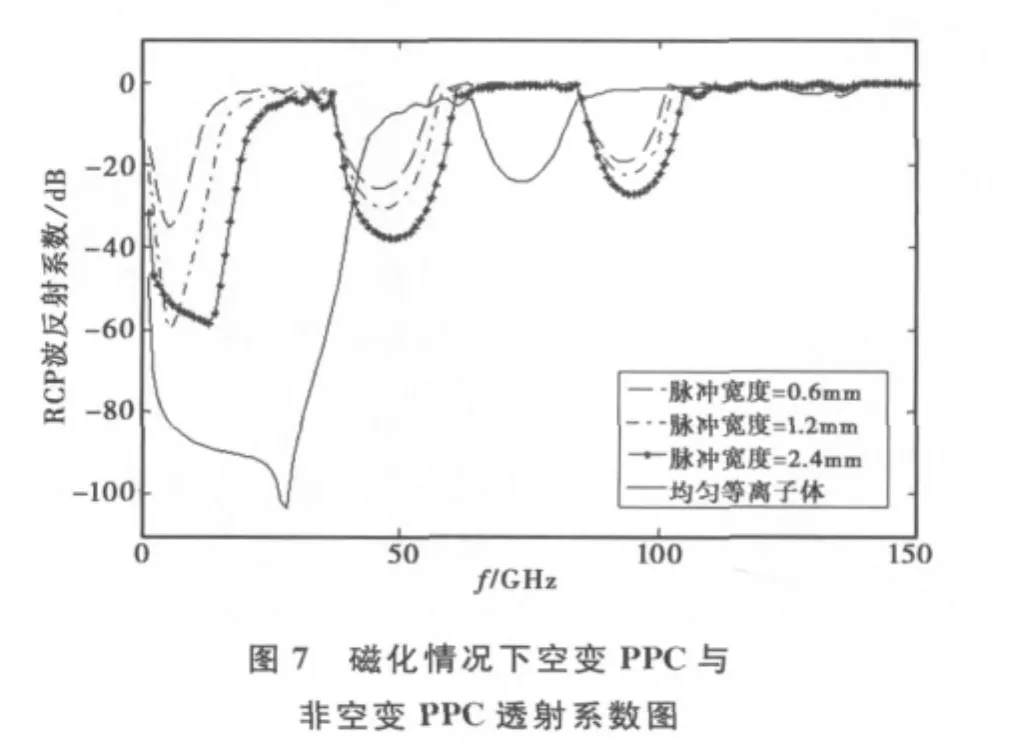
由图6、图7可以看到出：在磁化情况下，无论是反射系数还是透射系数，其等离子体光子晶体的禁带仍然随着高斯脉冲函数宽度（k）的变化而有规律的变化，随着k的逐渐变小光子晶体的禁带逐渐变大，但光子晶体的周期性并没有改变.这说明通过改变ωp（z）的高斯脉冲形式的函数宽度对PPC结构的禁带形成是可控的.

5 结 论

采用改进的磁化等离子体电磁波传播的FDTD算法研究了一维空变等离子体光子晶体的禁带特性.以微分高斯脉冲为激励源，引入了Mur吸收边界.用算法公式所得的电磁波反射系数来讨论随空间变化的等离子体频率对其禁带特性的影响.结果表明，对于光子晶体禁带的形成和产生，通过对等离子体空间频率的变化，能对禁带的周期性和宽度进行控制.等离子体频率随空间成高斯脉冲形式的函数变化，当脉冲宽度减小，其禁带的宽度也越小，脉冲宽度越大，禁带的宽度也越大.因此，要实现对等离子体光子晶体禁带的控制，可以通过改变等离子体频率的大小来获得.

［1］YABLONOVITCH E.Inhibited spontaneous emission in solid-state physics and electronics ［J］.Phys Rev Lett，1987，58（20）：2059-2062.

［2］JOHN S.Localization of photons in certain disordered dielectric super lattices［J］.Phys Rev Lett，1987，58（23）：2486-2489.

［3］梅洛勤，叶卫民，曾 淳，等.用传输矩阵法（TMM）研究二维光子晶体传输特性［J］.量子光学学报，2003，9（2）：88-92.MEI Luoqin，YE Weimin，ZENG Chun，et al.Characteristic properties of transmission research of 2-D photonic crystals using the transfer matrix method（TMM）［J］.Acta Sinica Quanturn Optica，2003，9（2）：88-92.（in Chinese）

［4］欧阳征标，安鹤男，阮双琛，等.利用二维光子晶体提高波的耦合效率［J］.光子学报，2004，33（1）：69-72.OUYANG Zhengbiao，AN Henan，RUAN Shuangchen，et al.Promoting the coupling efficiency of waves by a 2D photonic crystal［J］.Acta Photonica Sinica，2004，33（1）：69-72.（in Chinese）

［5］吴维庆，陈雄文，周 辉，等.混合纤芯光子晶体光纤超平坦色散的研究［J］.光子学报，2006，35（1）：109-113.WU Weiqing，CHEN Xiongwen，ZHOU Hui，et al.Investigation of the ultraflattened dispersion in photonic crystal fiberswithhybrid cores［J］.Acta Photonica Sinica，2006，35（1）：109-113.（in Chinese）

［6］李 岩，郑瑞生，冯玉春，等.一种发光二极管模型中无序光子晶体对光输出影响的研究［J］.光子学报，2006，35（6）：903-905.LI Yan，ZHENG Ruisheng，FENG Yuchun，et al.Influence of disordered photonic crystal on Light extraction of a kind of light emitting diode model［J］.Acta Photonica Sinica，2006，35（6）：903-905.（in Chinese）

［7］陈 松，王维彪，梁静秋，等.二维点缺陷正方光子晶体的微腔结构［J］.发光学报，2007，28（1）：7-11.CHEN Song，WANG Weibiao，LIANG Jingqiu，et al.Two-dimensional square photonic crystal microcavitives［J］.Chinese Journal of Luminescence，2007，28（1）：7-11.（in Chinese）

［8］王政平，王 成.含负折射率材料的一维"啁啾"光子晶体的透射谱［J］.发光学报，2008，29（2）：221-224.WANG Zhengping， WANG Cheng. Transmission spectrum of one-dimensional"Chirped"photonic crystal containing negative re-fraction materials［J］.Chinese Journal of Luminescence，2008，29（2）：221-224.（in Chinese）

［9］李洪涛，邵明珠，罗诗裕.介电常数呈正弦平方规律变化的一维光子晶体带结构［J］.发光学报，2008，29（2）：229-232.LI Hongtao，SHAO Mingzhu，LUO Shiyu.Band structure of one-dimensional photonic crystal with dielectric constant as a sine-squared function in coordinate space［J］.Chinese Journal of Luminescence，2008，29（2）：229-232.（in Chinese）

［10］HOJO H，MASE A.Dispersion relation of electro magnetic wave in one-dimensional plasma photonic crystals［J］.J Plasma Fusion Res，2004，80（2）：89-92.

［11］杨 娟，梁昌洪，李乐伟.二维光子晶体的负折射现象［J］.电波科学学报，2005，12（6）：703-706.YANG Juan，LIANG Changhong，LI Lewei.Negative refractive behaviors of two-dimensional photonic crystals［J］.Chinese Journal of Radio Science 2005，12（6）：704-706.（in Chinese）

［12］刘少斌，顾长青，周建江，等.磁化等离子体光子晶体的FDTD 分 析 ［J］.物 理学 报，2006，54（6）：2804-2808.LIU Shaobin，MO Jingjun，YUAN Naichang et al.FDTD simulation for magnetized plasma photonic crystals［J］.Acta Phys.Sin，2005，54（6）：2804-2808.（in Chinese）

［13］莫锦军，刘少斌，袁乃昌.非均匀等离子体覆盖目标隐身研究［J］.电波科学学报，2002，17（1）：69-73.MO Jinjun，LIU Shaobin，YUAN Naichang.On the stealth effect of non-uniform plasma covered radar targets［J］.Chinese Journal of Radio Science，2002，17（1）：69-73.（in Chinese）

［14］林宝勤，袁乃昌.二维金属型光子晶体的有限差分法分析［J］.电波科学学报，2006，21（2）：233-237.LIN Baoqin，YUAN Naichang.Finite difference analysis of 2-D metallic photonic crystals［J］.Chinese Journal of Radio Science，2006，21（2）：233-237.（in Chinese）

［15］刘 崧，刘少斌.非均匀分布等离子体光子晶体带隙分析［J］.核聚变与等离子体物理，2009，29（4）：365-369.LIU Song，LIU Shaobin.Analysis of photonic band gap in inhomogeneous plasma photonic crystals［J］.Nuclear Fusion and Plasma Physics，2009，29（4）：365-369.（in Chinese）

［16］SAKAI O.Verification of a plasma photonic crystal for microwaves of millimeter wavelength range using two-dimensional array of columnar microplasmas［J］.Appiled Physics Letters，2005，83（24）：505-508.

［17］XU Lijun，YUAN Naichang.JEC-FDTD for 2-D conducting cylinder coated by anisotropic magnetized plasma［J］.Microwave and Wireless Components Letters，2005，15（12）：892-894.

［18］DIKSHITULU K K.Eleectromagnetics of Complex Media Frequency Shifting by a Transient Magnetoplasma Medium［M］.New York：CRC press，1998：11-37.