海上湍流对雷达波传播影响模拟研究

戴福山

（北京应用气象研究所，北京100029）

引 言

雷达波在海洋大气近地层内传播不仅受大气折射指数垂直梯度引起的折射影响，还受大气湍流引起的大气折射率起伏脉动影响.海洋大气近地层内，因受水汽蒸发影响，大气折射指数自海面向上迅速递减，导致雷达波传播路径迅速向下弯曲，形成蒸发波导传播.蒸发波导可以使雷达波以很小损耗贴海面向前传播，从而可使舰载雷达对海面目标实现超视距探测.国内已经对蒸发波导形成机理、蒸发波导对电波传播影响，以及蒸发波导反演技术等开展了广泛研究［1-4］.湍流运动是海洋大气近地层的显著特征之一，湍流脉动引起的大气折射指数和大气折射率随机起伏对雷达波产生散射效应.Ivannov等人［5］指出海洋大气近地层内湍流散射效应会减弱蒸发波导传播效应，使蒸发波导内远距离处雷达波传播损耗增强.Barrios［6］研究表明海洋大气近地层内湍流散射效应，可引起雷达波传播损耗的随机起伏，影响舰载雷达对海面和低空目标的探测稳定性和置信水平.国内孙方等人［7］通过利用微波测距机连续测距，反算出海面大气折射率起伏变化，并将大气折射率扰动项分别加入抛物方程模型和射线追踪算法中计算了湍流环境下传播损耗和射线轨迹，结果表明，海上波导传播计算模型中考虑折射率扰动项，可以更加合理地进行雷达系统效应评估.

将基于海洋大气近地层相似理论，建立大气折射率及其结构常数垂直廓线模型；基于一维Kolmogorov湍流谱，数值模拟瞬变大气折射指数，并建立考虑湍流起伏的大气修正折射率垂直廓线；利用海面水文气象观测数据，借助于美国海军高级传播模型（Advanced Propagation Model，APM）［8］，数值模拟海洋大气近地层蒸发波导和湍流对雷达波传播和舰载雷达探测性能的影响.

1 近地层大气折射率垂直廓线

根据近地层相似理论，近地层内水平风速u、位温θ、比湿q的垂直廓线表达式为［9］：

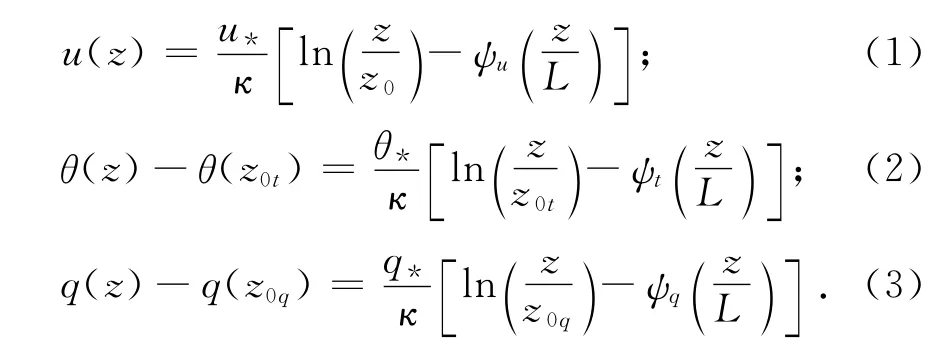
式中：u＊、θ＊、q＊分别是水平风速u、位温θ、比湿q的特征尺度；κ是von Karman常数；z为垂直高度；z0、z0t、z0q分别是水平风速、位温和比湿的粗糙度高度；ψu、ψt、ψq分别是水平风速、位温和比湿对应的普适函数；L 是长度尺度；u（z）、θ（z）、q（z）分别是高度z处的水平风速、位温和比湿；θ（z0t）、q（z0q）分别是粗糙度高度的位温和比湿.

稳定层结条件下，普适函数采用北冰洋海面热收支试验（Surface Heat Budget of the Arctic O-cean，SHEBA）研究成果［10］：

式中：x＝（1＋ζ）1/3；ζ＝z/L；am＝5；bm＝am/6.5；Bm＝［（1-bm）/bm］1/3；

式中：ah＝bh＝5；ch＝3；ζ＝z/L；Bh＝.不稳定层结下，普适函数采用以下诸式确定

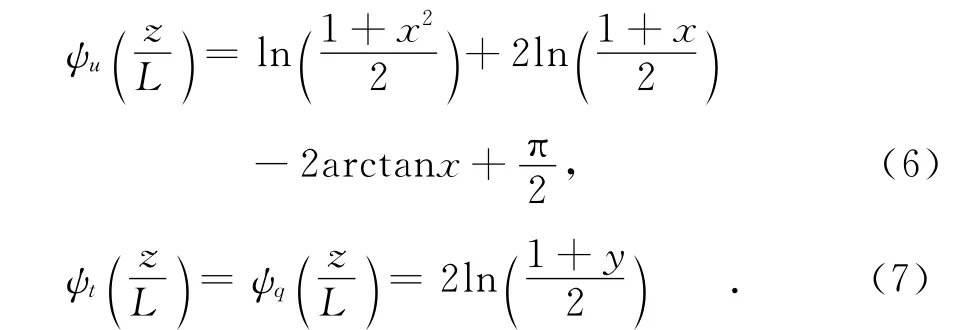
若有海面温度及海面参考高度处气温、气压和湿度观测数据，利用式（1）～（3）可以确定u＊、θ＊、q＊、L，进而可以给出海洋大气近地层水平风速u、位温θ、比湿q的垂直廓线［9，11］.利用位温θ（z）与温度T（z）间关系式，以及比湿q（z）与水汽压e（z）间关系式，可以得到温度T（z）和水汽压e（z）的垂直廓线.

海洋大气近地层内大气折射率N垂直廓线由下式确定

式中：P（z）为气压，单位为hPa；e（z）为水汽压，单位为hPa；T（z）为气温，单位为K.大气折射率与大气折射指数的关系为

在电波传播模型中通常采用大气修正折射率M，其定义为

式中：ae为地球半径，单位为m；z为海拔高度，单位为m.大气修正折射率M最小值所对应的高度就是蒸发波导高度d.

2 近地层大气折射指数结构常数垂直廓线

忽略气压扰动，大气折射指数n的扰动可以近似为

式中，（）′表示湍流扰动量.记温度T和比湿q的结构常数分别为C2T和C2q，温度与比湿交叉结构常数为CTq，大气折射指数结构常数C2n可以表示为

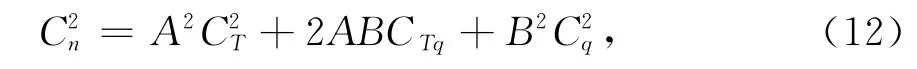
式中：

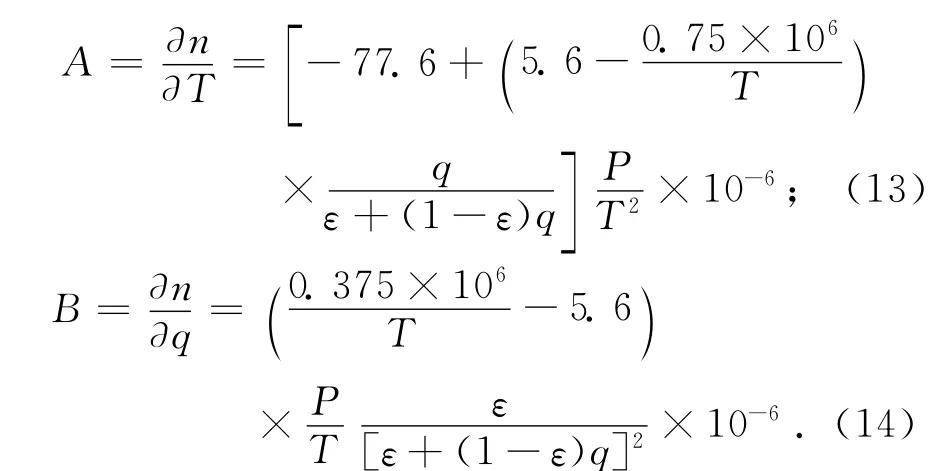
式中，ε＝0.622.

温度和湿度结构常数C2T、C2q及其交叉结构常数CTq可以用大气近地层温度特征尺度T＊和湿度特征尺度q＊表示为［12-13］

Andreas［14］和 Hill［15］等认为

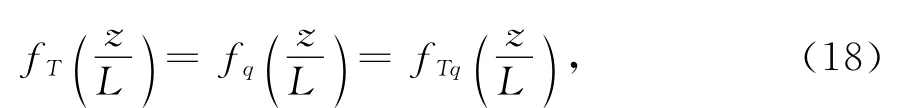
根据海上观测，Edson和Fairall［16］指出在不稳定层结条件 （z/L＜0）下可以用下式很好地描述

对于稳定层结 （z/L＞0），采用Frederickson［13］使用的表达式

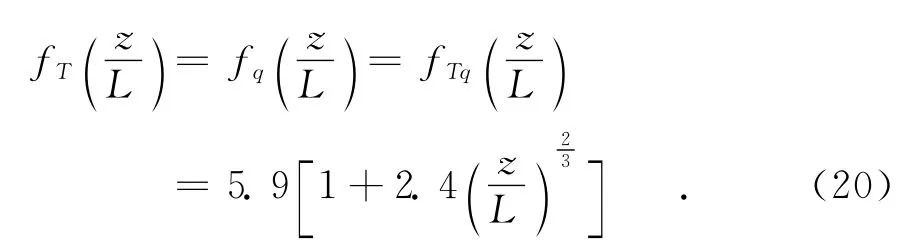
由于CTq的符号由T＊和q＊的乘积决定，因此，在方程（16）中取rTq为其绝对值.陆地和海面的观测表明：当感热通量与潜热通量之比（即Bowen比）为正值时，rTq≈0.8［17-18］；当 Bowen比为负值时，｜rTq｜≈0.5［17-18］.此 处 同 Frederickson［13］，取rTq如下：

式中：ΔT＝Ta-Ts，Ta、Ts分别是观测的气温和海表面水温；Δq＝qa-qs，qa、qs分别是对应于温度Ta和Ts的比湿.

3 考虑湍流影响大气修正折射率垂直廓线

假设大气湍流是充分发展并各向同性的，在惯性子区内其一维Kolmogorov谱用下式表示［19］：

式中：C2n是大气折射指数结构常数；k是湍流波数；L0、l0分别是湍流外尺度和内尺度.通过选择与湍流谱相匹配的振幅可以构造瞬变大气折射率nf为［19］

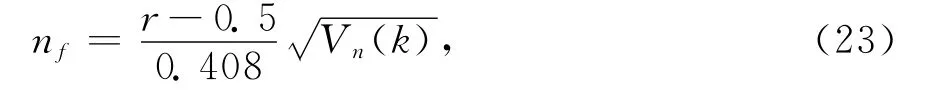
式中r为位于区间［0，1］内的均匀分布随机数.采用该方法模拟的瞬变大气折射率nf均值为0、方差为Vn.

利用海面水文气象观测数据，由式（12）以及式（15）～（17）可给出海洋大气近地层内不同高度z处大气折射指数结构常数C2n，再利用式（22）～（23），可以数值模拟不同高度z处大气折射指数起伏量nf.考虑大气折射指数起伏的瞬时大气折射指数可以表示为

将式（24）代入式（9）和（10），经整理后有：

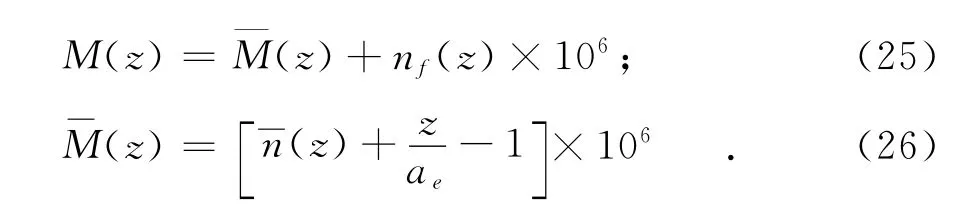
4 雷达波传播损耗数值计算

采用美国海军开发研制的高级传播模型［8］数值计算雷达波传播损耗.在分步抛物方程传播模型中，距离x＋Δx、高度z处的场量U（x＋Δx，z）由下式确定

式中：k0是自由空间波数；Δx为步长；m为大气修正折射指数；U（x，z）是距离x、高度z处的场量；p为傅里叶变换变量；F和F-1分别表示傅里叶正变换和逆变换.

由式（27）可知，利用前一步场量和大气介质特性，可以计算下一步场量.大气介质的特性体现在大气修正折射指数m（x＋Δx，z）上.利用大气修正折射指数m与大气折射指数n关系式，并利用式（9）、（10）和（25），式（27）变形为

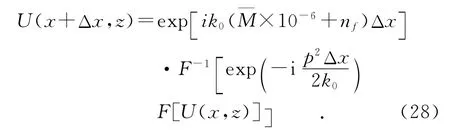
5 数值模拟分析

利用2000年1月7日15时某海域海面水文气象观测数据和假想雷达技术参数以及目标参数，数值模拟海洋大气近地层蒸发波导和湍流对雷达波传播以及雷达探测性能的影响.

假设某舰载雷达为简单脉冲雷达，雷达技术参数：频率为10GHz、天线高度为15m、天线仰角为0°、峰值功率为230kW、脉冲宽度为1.3μs、脉冲重复频率为640Hz、天线类型为sin（x）/x、天线水平扫描率为15rpm、波束水平宽度为1.5°、波束垂直宽度为16°、天线增益为30dB、天线噪声指数为14 dB、各种系统损耗为3dB、虚警概率为10-8；假设海面目标为小型运输船，其起伏类型为稳定型，雷达散射截面为50m2.

某海域海面水文气象观测条件是：气压为1 012.28hPa、气温为24.5℃、海面水温为24.2℃、海面相对湿度为79.5%、海面风速为6.6m/s.利用该海面水文气象数据计算分析的海洋大气近地层内微波波段湍流强度C2n常用对数lg（C2n）随垂直高度的变化如图1所示.由图1可见，在海面附近湍流强度最强，随垂直高度增加湍流强度逐渐减弱.

图1 海洋大气近地层微波湍流强度C2n估算值

分别在不考虑湍流影响（光滑实线）和考虑湍流影响（折线）时，利用海面水文气象观测数据估算的大气修正折射率垂直廓线如图2所示.未考虑大气湍流影响时大气修正折射率最小值所对应的高度就是蒸发波导高度，见图2中虚线，约13m.

图2 海洋大气近地层未考虑湍流和考虑湍流时大气修正折射率廓线图

将图2中未考虑湍流影响和考虑湍流影响的大气修正折射率垂直廓线输入高级传播模型计算的雷达波传播损耗分别见图3（a）和（b）.

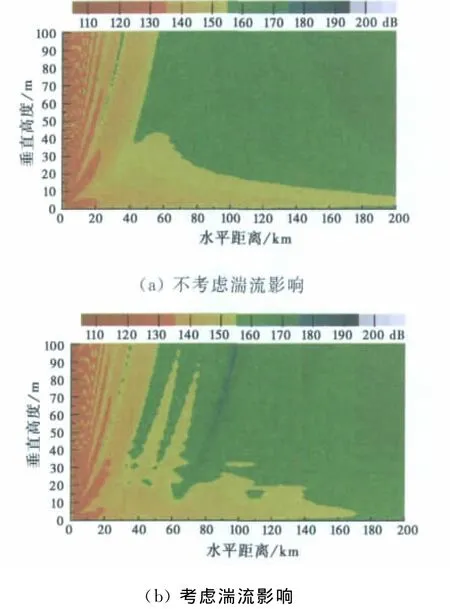
图3 10GHz雷达波传播损耗随距离和高度变化图

由图3可以看出：海洋大气近地层湍流效应显著减弱了蒸发波导传播效应，尤其在离发射源较远距离上，湍流效应显著增大了蒸发波导内雷达波传播损耗，在200km处增大近5dB；而在蒸发波导顶部分空域，湍流效应则一定程度上减弱了雷达波传播损耗.这可能是由于湍流效应局部改变了大气修正折射率垂直梯度，导致部分雷达波穿越蒸发波导到达蒸发波导高度以上空间，从而造成蒸发波导内雷达波能量泄漏，雷达波传播损耗增大，而蒸发波导顶部分空间，雷达波能量则有所增强.该结论与Ivanov等人［5］结论一致.

在不考虑和考虑海洋大气近地层湍流影响条件下，基于以上雷达波传播损耗计算结果，计算分析给定雷达在给定海面水文气象条件下对给定目标的探测威力图，如图4（a）、（b）所示.比较图4（a）和图4（b）可以看出，海洋大气近地层湍流效应减弱了舰载雷达对海面目标的探测性能，使雷达对海面目标的探测能力随距离出现显著起伏变化.

图4 给定雷达对给定目标的探测威力图

为了更进一步认识该问题，图5（a）和（b）分别给出了在不考虑和考虑海洋大气近地层湍流影响条件下雷达波在10m高度传播损耗随距离变化图，同时用三条虚线分别给出了该雷达对给定目标在10%（红色）、50%（蓝色）和90%（绿色）探测概率下的阈值损耗.

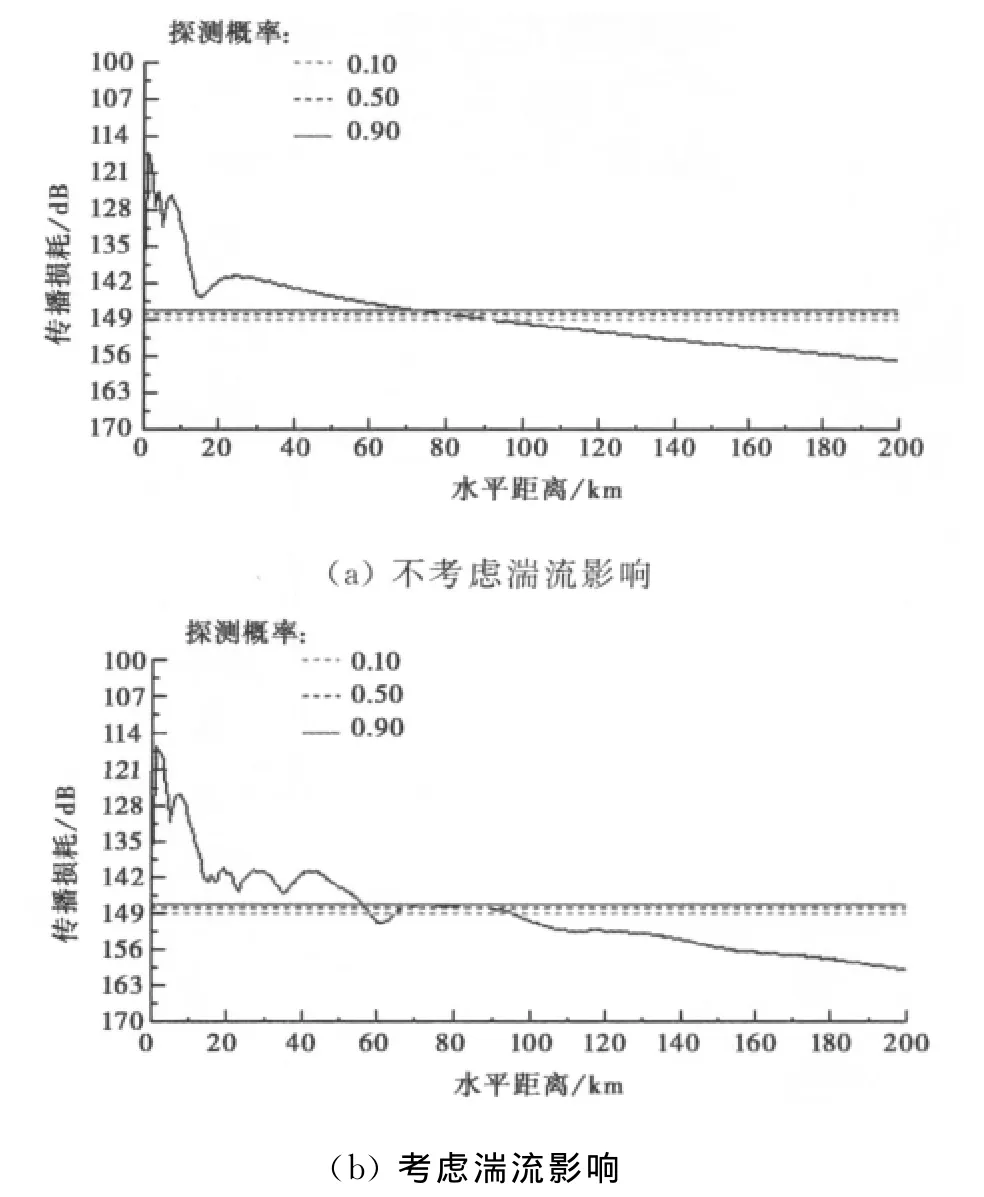
图5 雷达波在10m高度传播损耗随距离变化图

由图5可看出：考虑海洋大气近地层湍流影响效应后，10km以外雷达波传播损耗比不考虑湍流影响时增大，而且雷达波传播损耗随距离存在显著的起伏变化.由于湍流效应增大了蒸发波导内雷达波传播损耗，因此，减弱了雷达探测性能.在不考虑湍流影响效应时，雷达对10m高度雷达散射截面为50m2目标90%探测概率下的探测距离最大可达72km左右，在72km距离内雷达可以稳定探测到目标；但考虑海洋大气近地层湍流效应影响后，该雷达对同一高度同一目标在90%探测概率下可以稳定探测目标的最大探测距离约56km左右，比不考虑湍流影响效应时减小了约16km；但在70km附近，雷达波传播损耗与90%探测概率对应的阈值损耗几乎重合；尤其值得注意的是在60km距离附近，雷达波传播损耗显著大于90%探测概率对应的阈值损耗，在此距离附近雷达探测不到目标.

6 结 论

基于海洋大气近地层相似理论给出了大气折射率和微波波段湍流强度垂直廓线模型；在假设大气湍流是充分发展和各向同性条件下，通过选择与湍流谱相匹配的振幅数值模拟了瞬变大气折射指数；并基于海洋大气近地层大气修正折射率廓线模型，利用海面水文气象观测数据和美国海军高级传播模型，数值模拟了海洋大气近地层内蒸发波导和湍流对10GHz雷达波传播和雷达探测性能影响.结果发现：海洋大气近地层内湍流在一定程度上减弱了蒸发波导传播效应，尤其在离发射源较远距离上，湍流效应显著增大了蒸发波导内雷达波传播损耗，在200km处传播损耗增大接近5dB，从而减小了雷达超视距探测距离；而在蒸发波导顶部分空域，湍流效应在一定程度上减弱了雷达波传播损耗.这可能是由于湍流效应局部改变了大气修正折射率垂直梯度，导致部分雷达波穿越蒸发波导到达蒸发波导高度以上空间，从而造成蒸发波导内雷达波能量泄漏，雷达波传播损耗增大，而蒸发波导顶部分空域，雷达波能量则有所增强.因此，在定量评估舰载雷达对海面和低空目标探测性能时有必要同时考虑蒸发波导和湍流的综合影响.

需要说明的是：本文数值模拟结果有待进一步利用舰载雷达试验数据进行检验验证；此外，本文主要考虑海洋大气近地层湍流对雷达波传播影响，海洋大气边界层顶部湍流效应对雷达波传播影响有待于进一步研究.

致谢：感谢美国海军提供高级传播模型（APM）.

［1］戴福山，李 群，董双林，等.大气波导及其军事应用［M］.北京：解放军出版社，2002.

［2］戴福山.海洋大气近地层折射指数模式及其在蒸发波导分析上的应用［J］.电波科学学报，1998，13（3）：280-286.DAI Fushan.The refractivity models in the marine surface layer and their applications in the evaporation duct analysis［J］.Chinese Journal of Radio Science，1998，13（3）：280-286.（in Chinese）

［3］刘爱国，察 豪.海上蒸发波导条件下电磁波传播损耗实验研究［J］.电波科学学报，2008，23（6）：1199-1203.LIU Aiguo，CHA Hao.Experiments study of electromagnetic wave propagation loss in oceanic evaporation duct［J］.Chinese Journal of Radio Science，2008，23（6）：1199-1203.（in Chinese）

［4］张金鹏，吴振森，赵振维，等.基于不同天线高度雷达海杂波的蒸发波导反演［J］.电波科学学报，2011，26（3）：422-430.ZHANG Jinpeng，WU Zhensen，ZHAO zhenwei，et al.E-vaporation duct inversion based on radar sea clutters from different antenna heights［J］.Chinese Journal of Radio Science，2011，26（3）：422-430.（in Chinese）

［5］IVANNOV V K，SHALVAPIN V N，LEVADNY Y V.Microwave scattering by tropospheric fluctuations in an evaporation duct［J］.Radiophysics and Quantum Electronics，2009，52（4）：277-286.

［6］BARRIOS A.Modeling surface layer turbulence effects at microwave frequencies［C］//Proceedings of IEEE Radar Conference.Rome，May 26-30，2008：1-6.

［7］孙 方，赵振维，王红光，等.海上湍流效应对大气波导传播的影响［J］.现代雷达，2011，33（2）：13-17.SUN Fang，ZHAO Zhenwei，WANG Hongguang，et al.Influence of turbulence effect on atmospheric duct propagation over sea.Modern Radar，2011，33（2）：13-17.（in Chinese）

［8］BARRIOS A，PATTERSON W L.Advanced Propagation Model（APM）Ver.1.3.1Computer Software Configuration Item（CSCI）Documents［R］.San Diego：Space and Naval Warfare Systems Center，2002.

［9］FAIRALL C W，BRADLEY E F，ROGERS D P，et al.Bulk parameterization of air-sea fluxes for tropical oceanglobal atmosphere coupled-ocean atmosphere response experiment［J］.Journal of Geophysics Research，1996，101（C2）：3747-3764.

［10］GRACHEV A，ANDREAS E L，FAIRALL C W，et al.SHEBA flux-profile relationships in the stable atmospheric boundary layer［J］.Boundary-Layer Meteorology，2007，124（3）：315-333.

［11］LIU W T，KATSAROS K B，and BUSINGER J B.Bulk parameterization of air-sea exchanges of heat and water vapor including the molecular constraints at the interface［J］.Journal of the Atmospheric Science，1979，36（9）：1722-1735.

［12］DAVIDSON K L，SCHACHER G E，FAIRALL C W，et al.Verification of the bulk method for calculating overwater optical turbulence［J］.Applied Optics，1981，20（17）：2919-2924.

［13］FREDERICKSON PAUL A，DAVIDSON K L，ZEISSE C R，et al.Estimating the refractive index structure parameter（C2n）over the ocean using bulk methods［J］.Journal of the Applied Meteorology，2000，39（10）：1770-1783.

［14］ANDREAS E L.Estimating C2nover snow and sea ice from meteorological data［J］.Journal of the Optics Society of the America，1988，5（4）：481-495.

［15］HILL R J.Implications of Monin-Obukhov similarity theory for scalar quantities［J］.Journal of the Atmospheric Science，1989，46（14）：2236-2244.

［16］EDSON J B and FAIRALL C W.Similarity relationships in the marine atmospheric surface layer for terms in the TKE and scalar variance budgets［J］.Journal of the Atmospheric Science，1998，55（13）：2311-2328.

［17］FAIRALL C W，SCHACHER G E，DAVIDSON K L.Measurements of the humidity structure function parameters，C2qand CTq，over the ocean［J］.Boundary-Layer Meteorology，1980，19（1）：81-92.

［18］ANDREAS E L，HILL R J，GOSZ J R，et al.Statistics of surface-layer turbulence over terrain with metre-scale heterogeneity［J］.Boundary-Layer Meteorology，1998，86（3）：379-408.

［19］HERBERT V HITNEY.A practical tropospheric scatter model using the parabolic equation［J］.IEEE Transactions on Antennas and Propagation，1993，41（7）：905-909.