复杂媒质目标电磁散射问题的有限元分析

彭文峰 宛 汀 郁美艳

（南京理工大学，江苏 南京210094）

引 言

随着微波和光学工程的迅速变革，以及人工合成媒质技术的不断发展，复杂电磁媒质的研究受到越来越多的重视.选择和运用恰当的电磁场问题的数值计算方法对复杂电磁媒质进行研究有着重要的理论意义和工程应用价值.在一些传统的数值计算方法中，使用积分方程法如矩量法的算法，往往导致复杂的格林函数，有时候格林函数甚至是不可得的.使用时域有限差分法（FDTD）时，因为需要计算额外的时间导数而变得不稳定.用于分析平面分层结构的谱域法与直线法也需要重新计算格林函数.虽然利用场分解特性［1］，可以将手征材料等效成两个没有耦合的简单材料进行计算，但是这种方法却不能应用到更具有通用形式的一般双各向异性媒质中.众所周知，有限元方法［2］是一种通用性很强的数值算法，它能灵活地适应物体几何结构和材料的变化.与FDTD相比，有限元法更适用于分析任意不均匀复杂结构.而与矩量法相比，使用有限元算法计算双各向异性媒质的优点在于推导双各向异性的泛函公式相对比较简单，有较强的复杂媒质的处理能力.而且，有限元方法生成的线性方程组的系数阵为稀疏矩阵，节省了内存.因此，本文研究将有限元方法发展应用到含有复杂媒质结构的电磁散射问题中，包括各向异性媒质、双各向同/异性媒质，并验证其准确性和通用性.

本文建立了具有一般通用形式的线性媒质——双各向异性媒质［3］的有限元泛函公式模型，采用完全匹配层［4］来截断散射问题开放区域，并推导了有限元矩阵方程的具体表达式.然后，运用该方法对四种典型的复杂媒质结构散射问题进行了数值计算，并将计算结果和相关文献进行比较.结果证明，有限元方法能很好地解决含有各向异性、双各向同性以及双各向异性的各种复杂媒质目标电磁散射的数值仿真问题.本文的研究工作具有较强的通用性，能够对多种复杂媒质目标进行分析，在研究雷达目标隐身和反隐身技术、复杂天线系统设计、现代电子系统的电磁兼容性分析等领域均能有效地发挥作用.

1 基本理论

对于复杂媒质，其本构关系为

图1给出了一个典型的采用有限元方法分析电磁散射问题的示意图.我们采用完全匹配层（PML）作为区域截断边界条件.在PML区域内，有效磁导率和介电常数为对角矩阵的形式.对于z方向的PML，强加如下约束条件

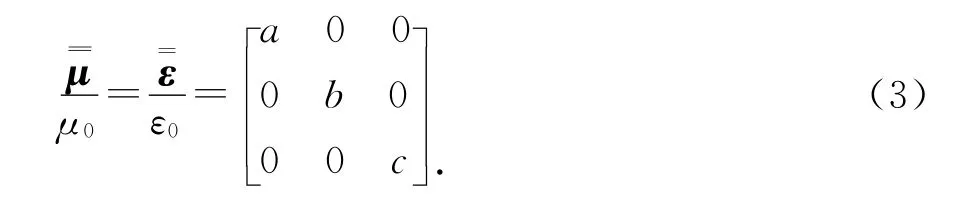
图1 三维目标的散射

假定波的传播方向为z，当bc＝1，a＝b时，可以得到0反射.为了使入射波充分的衰减，a、b、c应取作复数.令a＝b＝1/c＝α-jβ，α决定了此介质中的波长，β决定了波的衰减程度.则PML内的相对磁导率与电导率可以表示为

PML参量的取值依赖于波的传播方向和PML层本身的位置（PML层可以设在面、边或者角落）.针对二维和三维问题时，我们选择不同的ε＝r和＝μr应用于不同的方向.棱边和体角落含有特殊的张量，例如放于棱边，则对于z方向上的一条棱边，应选择r和r的值为r＝r＝［μr］x×［μr］y；放在体角上，则为三个方向上的各张量的乘积.

由复杂媒质的本构关系以及麦克斯韦方程组推导出双各向异性媒质的电场波动Helmholtz方程为

对于复杂媒质，有限元泛函可以写为［2］

由于式（6）的工作变量是总场，在散射问题中有总场E＝Esc＋Einc，其中Esc为散射场，Einc为入射场，因此式（6）也可以写为

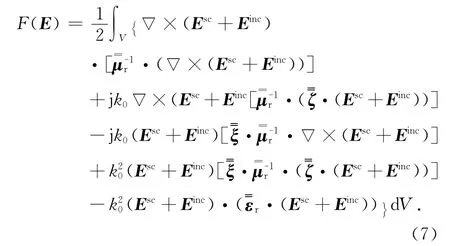
又因Einc为已知场，在变分公式求偏导时等于零，因此式（7）中只含Einc的项可以去掉，应用第一矢量格林定理，可得

式中：Vsc表示散射体的体积；Ssc表示散射体的表面；Einc为激励平面波.

在获得整个分析区域的泛函之后，接下来要进行的是区域离散的工作.选用灵活的四面体单元对整个区域进行离散，生成网格之后，根据选定的切向连续的矢量基函数（9）来建立有限元方程.

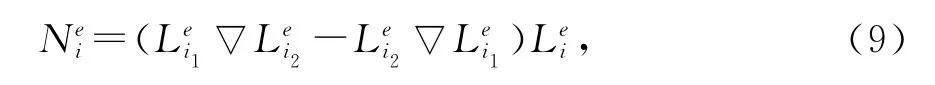
式中：i＝1，2，…，6，i表示第i条边；i1i2表示第i条边两个端点的编号；Li为体积坐标.

选择相同的基函数和加权函数Ni，可以得到复杂媒质的有限元散射公式为

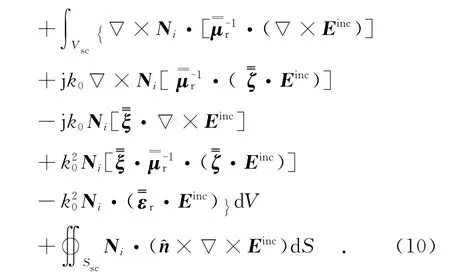
根据伽辽金方法，对于其单元每一棱边元的残数加权积分为0，结合式（10），得到整个e单元的矩阵形式为

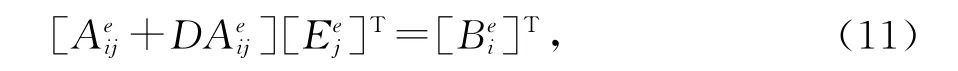
式中：

其中，

式中，

由方程（11）解得散射场Esc（近场）之后，在远处r的散射场Esc（r）（远场）就可以使用等效原理求解，即

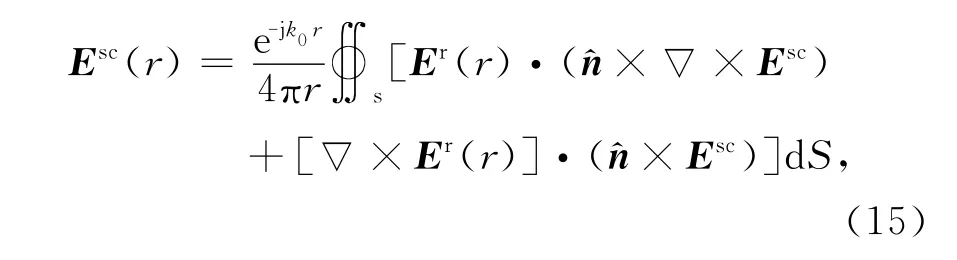
式中：S是包围散射体的任意闭合曲面；Er为等效的无穷远处入射的平面波，其表达式为

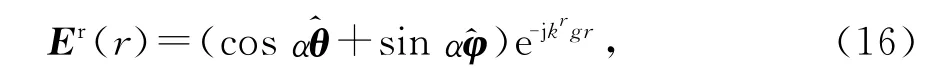
其中α为极化角，当α＝0时入射波为θ极化，α＝π/2时入射波为φ 极化.kinc是传播矢量，θinc、φinc为激励平面波的入射角，有

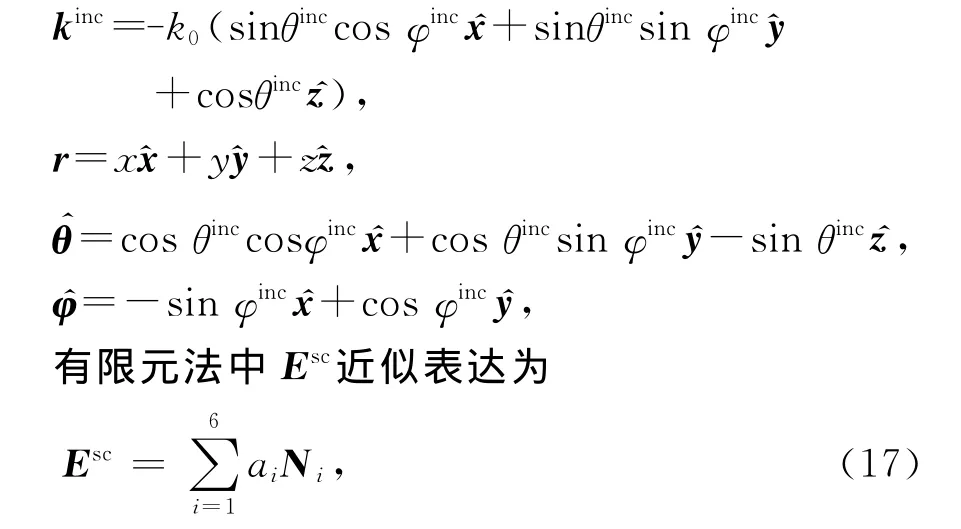
式中：Ni为基函数；ai为有限元方程已求出的基函数的系数.

将式（17）代入式（15）得到

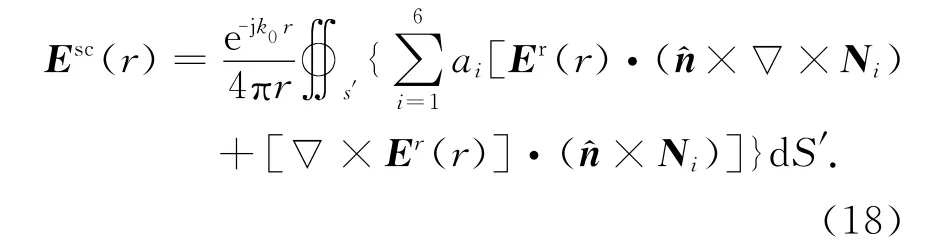
求出了远处r的散射场，就可以用雷达散射截面（RCS）表示物体的散射特性，雷达散射截面的定义为

由于入射场是平面波，因此有｜Einc（r）｜＝1，则式（19）可以写为

2 数值算例

下面计算几个典型的例子来证明本文方法的正确性和有效性.本文均采用PML作为区域截断边界条件，为保证PML良好的截断效果，算例中PML的厚度均取为0.25λ0，距离散射体为0.3λ0，λ0为自由空间波长，参数值取为α＝β＝1.5.

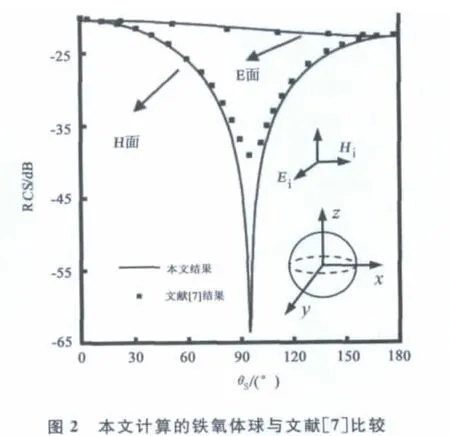
第一个例子分析的是电尺寸为k0a＝0.2π的铁氧体球.直角坐标系的原点位于球心，设外加偏置磁场在方向得到，即H0＝H0，入射的平面波沿z轴方向，其极化方向沿正x轴方向.各向异性铁氧体的介质参数为ε0（真空中的介电常数），其相应的导磁率为［5-6］，可表示为

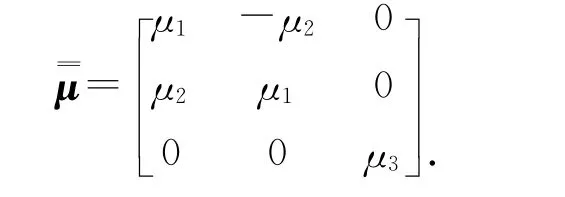
本例中，铁氧体的参数为μ1＝5μ0，μ2＝jμ0，μ3＝7μ0.图2为本文计算结果与文献［7］的比较，可以看出曲线有细小差别，其原因是本程序采用PML作为边界截断条件，一般情况下PML并不百分之百吸收，并且-35dB已经是一个很小的值了，所以该误差在允许的范围之内.

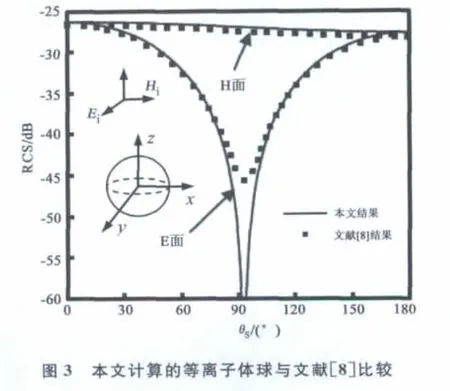
第二个例子是电尺寸为k0a＝0.5的等离子球，入射的平面波沿z轴正方向入射，其极化方向沿正x轴方向.各向异性等离子体的导磁率为μ0（真空中的导磁率），电容率可表示为

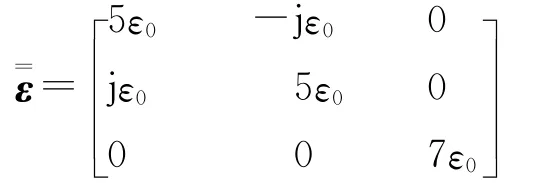
图3为本文结果与文献［8］的比较.可以看出，本程序计算的结果和文献结果在-40dB之上还是非常吻合的.由于本程序采用PML作为边界截断条件，一般来讲，PML是不能达到百分百吸收的，另外，-40dB是可以忽略的十分小的误差.

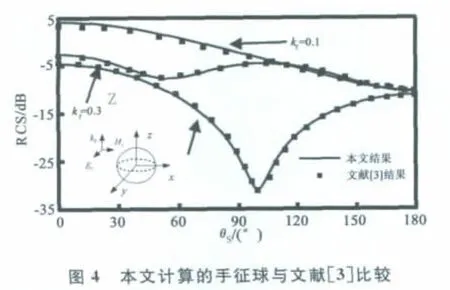
第三个例子是尺寸为k0a＝1.5的手征介质球.为了与文献对比，手征的本构关系可以写成如下形式

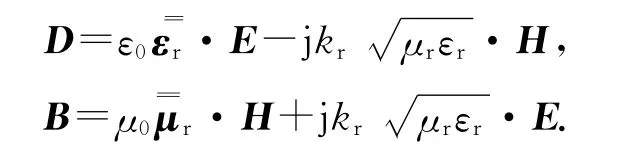
根据文献［3］，手征参数设为εDBF＝4ε0、μDBF＝μ0、ε＝εDBF/（1-k2r）、μ＝μDBF/（1-k2r）.入射的平面波沿z轴正方向，其极化方向沿正x轴方向.图4中的曲线对比再次验证了本程序的正确性.

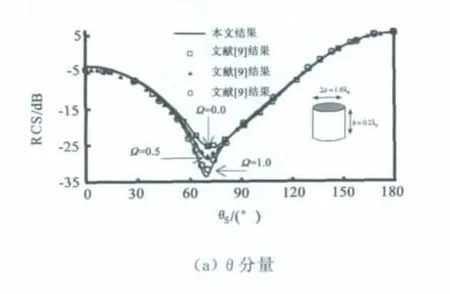
第四个例子是双各向异性媒质圆柱，底面半径为a＝0.5λ0，高度为h＝0.2λ0，双各向异性媒质参数具有如下张量形式入射的平面波沿z轴正方向，其极化方向沿正x轴方向.Ω 媒质参数为ε1＝2.0，ε2＝3.0，ε3＝2.0，μ1＝1.2，μ2＝1.2，μ3＝1.0，Ω＝0.0，0.5，1.0.图5中与文献［9］曲线的对比验证了本程序计算双各向异性媒质的正确性.

3 结 论

本文介绍了分析复杂媒质散射问题的有限元方法.有限元法适用于分析任意非均匀复杂结构，有较强的复杂媒质的处理能力，生成的线性方程组的系数阵为稀疏矩阵，节省了存储量.算例的数值分析表明，该方法的计算结果与文献结果吻合较好，从而证明了其正确性和有效性.此外，该方法适用范围广，不仅能够用来计算各向异性媒质的散射特性，对双各向同性和双各向异性媒质同样适用，是一种通用性较强的方法.

［1］AL-KANHAL M A，ARVAS E.Electromagnetic scattering from a chiral cylinder of arbitrary cross section［J］.IEEE Trans Antennas and Propagation，1996，44（7）：1041-1048.

［2］金建铭，著.电磁场有限元方法［M］.王建国，葛德彪，译.西安：西安电子科技大学出版社，1998.

［3］周 平.脊加载椭圆波导传输特性的矢量有限元法分析［J］.电波科学学报，2009，24（6）：1164-1167.ZHOU Ping.Propagation characteristics analysis for ridged elliptical waveguide by vector finite-element method［J］.Chinese Journal of Radio Science，2009，24（6）：1164-1167.（in Chinese）

［4］孙向阳，聂在平，李爱勇，等.用高阶叠层矢量有限元法计算随钻测井的三维电磁响应［J］.电波科学学报，2009，24（2）：273-279.SUN Xiangyang，NIE Zaiping，LI Aiyong，et al.The modeling of logging-while-drilling tool’s three-dimensional electromagnetic response using the high order hierarchical vector finite element method［J］.Chinese Journal of Radio Science，2009，24（2）：273-279.（in Chinese）

［5］EDWARD K N，YUNG H Y，DING R S，et al.Finite-difference analysis of H-Plane waveguide Y-junction circulars［J］.Microwave and Optical Technology Letters，1999，20（6）：414-422.

［6］耿友林，吴信宝，官伯然.导体球涂覆各向异性铁氧体介质电磁散射的解析解［J］.电子与信息学报，2006，28（9）：1740-1743.GENG Youlin，WU Xinbao，GUAN Boran.The analytical solution to the electromagnetic scattering by an anisotropic ferrite-coated conducting sphere［J］.Journal of Electronics ＆Information Technology，2006，28（9）：1740-1743.（in Chinese）

［7］耿友林.球矢量波函数在各向异性介质散射中的应用［D］.西安：西安电子科技大学，2006.GENG Youlin.The application of the sphere vector wave function for the electro-magnetic scattering from the anisotropic media［D］.Xi’an：Xidian University，2006.（in Chinese）

［8］ZHANG Y，WEI X，LI E.Electromagnetic scattering from three-dimensional bi-anisotropic objects using hybrid finite element-boundary integral method［J］.J of Electromagn Waves and App，2004，18（11）：1549-1563

［9］OZGUN O，KUZUOGLU M.A non-iterative domain decomposition method for finite element analysis of 3D electromagnetic scattering problems［C］//IEEE Antennas and Propagation Society International Symposium.San Diego，July，5-11，2008：40-50.

［10］ZHU J，CHEN R S，FAN Z H，et al.Efficient preconditioner for the finite-element boundary integral analysis of electromagnetic scattering in the half space［J］.IET Microwaves Antennas ＆ Propagation，2010，4（3）：374-380.

［11］JACKSON S A，VOUVAKIS M N.Octree-based finite element method for electromagnetic scattering problems［C］//IEEE Antennas and Propagation Society International Symposium.Toronto，July，11-17 2010：1-4.

［12］ZHANG Ruigang，CHEN Huanzhen.An immersed finite element method for anisotropic flow models in porous medium［C］//International Conference on Information Science and Technology.Nanjing，March 26-28，2011：168-175.