基于乌鲁木齐物流产业分析多重共线性

李育冬，吴 昊，夏苏清

（1新疆大学 经济与管理学院，新疆 乌鲁木齐830046；2解放军69081部队，新疆 乌鲁木齐830000）

在经济学构建回归模型分析时，经典的简单最小二乘估计（OLS），必须满足高斯假设等苛刻的假设条件，而在实际分析经济学问题的时候，解释变量之间完全不相关的情形是十分少见的，由于经济学分析的社会问题往往涉及面广泛，考察的自变量多，当研究时间序列数据时候，大多数自变量随着时间变化往往存在共同的变化趋势，使得它们之间在某种程度上存在着一定的共线性；而对于截面数据常常也存在自变量高度自相关的情况，而存在着共线性会给模型带来许多不确定性的结果。

一、多重共线性的认识

（一）多重共线性的定义

设回归模型y＝β0＋β1x1＋β2x2＋…＋βpxp＋ε如果矩阵X的列向量存在一组不全为零的p＋1个数k0，k1，k2…kp使得k0＋k1xi1＋k2xi2＋…＋kpxip＝0，i＝1，2，…n，则称其存在完全共线性，如果k0＋k1xi1＋k2xi2＋…＋kpxip≈0，i＝1，2，…n，则称其存在多重共线性，也称复共线性。

（二）多重共线性的后果

多重共线性其实是由样本容量太小所造成的后果，当样本容量n很小的时候，多重共线性才是非常严重的。在不同口径下有关的许多变量，变量太多不但会增加计算的复杂性，而且也给全面合理地分析问题和解决问题带来很大困难，虽然每个变量都提供了一定的信息，但每个变量的重要性有所不同。当存在多重共线性时，自变量用来解释因变量所提供的信息出现重叠，多重共线性导致模型回归系数参数估计的标准误差变大，置信区间变宽，利用OLS估计得到的回归参数估计值很不稳定，回归系数的方差随着随着多重共线性强度的增加而加速增长，常常会出现在回归方程高度显著的情况之下，有些回归系数通不过显著性检验，还常常会出现回归系数正负号得不到合理的经济学解释。因此，在经济学研究之中构建多元回归模型考察因变量时要消除多重共线性的影响。［1］180-183

多重共线性的常见影响有：

（1）在存在多重共线性的情况下，得到的OLS估计结果是最优线性无偏估计的，但有较大的方差和协方差，估计精度不高，最突出的就是参数估计值的方差增大；

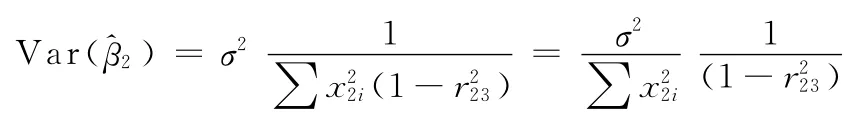
当r23增大时，Var（）也增大。

（2）对参数区间估计时，置信区间趋于变大，使得接受原假设H0的概率更大；

（3）假设检验容易作出错误的判断；

（4）可能造成拟合优度R2较高，但对各个参数单独的t检验却可能不显著，甚至可能使估计的回归系数符号相反，得出完全错误的结论，得不出合理的经济学解释。

（5）OLS估计量及其标准误对数据微小的变化也会很敏感。

（三）多重共线性产生的原因

（1）经济变量之间具有共同变化趋势。由于考察的自变量随时间变化往往有共同的变化趋势，往往受到共同因素的影响，各个自变量之间存在着共线性。例如当经济出现大繁荣时，反映经济情况的指标都有可能按着某种比例关系增长。

（2）模型中包含滞后变量。滞后变量的引入也会产生多重共线行，例如本期的消费水平除了受本期的收因素入影响之外，还有可能受前期的收入因素影响，建立模型时，本期的收入水平就有可能和前期的收入水平存在着共线性。

（3）利用截面数据建立模型也可能出现多重共线性。在经济学研究建立多元回归模型时利用的截面数据本身就有可能存在自相关性，如果没有进行处理建立的模型就有可能存在着共线性。

（4）样本数据采集方法的原因。

（四）多重共线性的识别

1.简单观察法

（1）在自变量的相关系数矩阵中，一些自变量的相关系数值比较大；

（2）回归系数的符号与经济学常识相反或者难以解释；

（3）重要考察的自变量的置信区间过大；

（4）如果增加一个变量或删除一个变量，回归系数的估计值发生了很大的变化；

（5）对重要的自变量的回归系数进行t检验，其结果不显著，但是F检验确得到了显著的通过。

2.方差扩大因子法（VIF）

3.特征根判定法

由于矩阵行列式的值等于其特征根的连乘积，因此当行列式｜X′X｜≈0时，至少有一个特征根为零，反过来，可以证明矩阵至少有一个特征根近似为零时，X的列向量必存在多重共线性，同样也可证明X′X有多少个特征根近似为零矩阵，X就有多少个多重共线性。根据条件数其中λ为最大的特征根，λ为其mi他的特征根，通常认为0＜K＜10，没有多重共线性，100＞K＞10存在着一般多重共线性，K＞100存在着严重多重共线性。

（五）多重共线性的处理方法

1.增加样本容量

当多重共线性出现是由于测量误差引起的，而不存在于总体样本时，通过增加样本容量可以减少或是避免线性重合，但是在现实的生活中，由于受到各种统计数据不足的限制，增加样本容量有时又是不现实的。

2.剔除法

当面当面临严重的共线性时，一种最简单的方法就是剔除掉一些不太重要的自变量，主要有向前法和后退法，逐步回归法。但决定保留或剔除哪些自变量并不是一件容易的事。因此，如何判断某个变量是否重要，是此方法的关键。从模型中删除一个变量，还可能导致设定偏误。此外，在一些经济模型中，要求一些很重要变量必须包含在里面，这时如果贸然的删除就不符合现实的经济意义。

3.主成分分析法

主成分分析一种处理严重共线性的有偏估计方法。当自变量间有较强的线性相关性时，利用p个变量的主成分，所具有的性质，如果他们是互不相关的，可由前m个主成Z1，Z2，…Zm来建立回归模型。

由原始变量的观测数据计算前m个主成分的得分值，将其作为主成分的观测值，建立Y与主成分的回归模型即得回归方程。这时p元降为m元，这样既简化了回归方程的结构，且消除了变量间相关性带来的影响。然而，主成分估计提取的主成分与因变量关系也不密切，使模型的拟合效果降低；而且以此同时主成分的实际含义也不明确。［2-3］

4.偏最小二乘法（PLS）

PLS法是由H.Wold在1966年提出的PLS是由Wold（1966）提出的，PLS≈主成分估计＋典型相关分析。PLS吸取了主成分估计的思想，提取的主成分考虑了对因变量的解释能力，使估计值优于主成分估计值。可是，与此同时PLS也继承了主成分估计的一些缺点，如主成分含义也不明确、信息重叠等现象。

5.岭回归法

岭回归分析是由Heer首先提出的，他与肯纳德合作，进一步发展了该方法，在多元线性回归模型的矩阵形式Y＝Xβ＋ε，参数β的普通最小二乘估计为β＝（X′X）-1X′Y，岭回归当自变量存在多重共线性｜X′X｜≈0时，给矩阵加上一个正常系数矩阵kI，那么β＝（X′X＋kI）-1X′Y，当时就是普通最小二乘估计。岭回归也是有偏估计方法。当出现严重共线性时，岭估计往往比OLS估计量更稳定，以及更小的协方差矩阵。岭估计的最大困难是最优k值的选择。尽管人们提出了许多确定k值的原则和方法，但理论上还未得到满意答案。此外，在实际应用中k值必须通过样本来确定，存在明显的主观性。［4］

二、处理多重共线性的实际运用

根据乌鲁木齐市统计年鉴［5］，选取乌鲁木齐市2000年至2012年的物流产业相关统计数据做一个多元回归模型，选取乌鲁木齐市的货运量周转量（Y）为因变量，进出口总额（X1）、社会消费品零售总额（X2）、物流业就业人数（X3）、公路里程（X4）、邮电业务收入（X5）5个变量为自变量，将所有变量加以对数化处理。构建多元回归模型为LNY＝β1LNX1＋β2LNX2＋β3LNX3＋β4LNX4＋β5LNX5＋ε……（3.1）；其中ε为随机干扰项。

1.简单最小二乘估计法

运用SPSS统计软件进行分析，从简单二乘法估计结果可以看到，调整的拟合优度R2＝1，F＝34880.71，在置信水平为95%，自由度4，方程通过了显著性的检验，从整体上来说方程得到了很好的拟合，通过筛选方程剔除了自变量LNX2，同时变量LNX1，LNX3不显著，LNX1系数为负，和经济学的原理相反。方差扩大因子VIF1＝2649.482，VIF2＝659.07917，VIF3＝1463.4738，VIF4＝1585.8618.均大于10说明存在多重共线性。再由多重共线性诊断结果可以看到，特征值有两个接近于零，最大条件数为120.408，且直观可以看出，第四个特征值的方差既可以解释LNX1方差的98%，也可以解释LNX3方差的86%，说明自变量间存在着严重的多重共线性。

2.运用岭回归解决多重共线性

用SPSS软件采用岭回归法做出的结果如下：

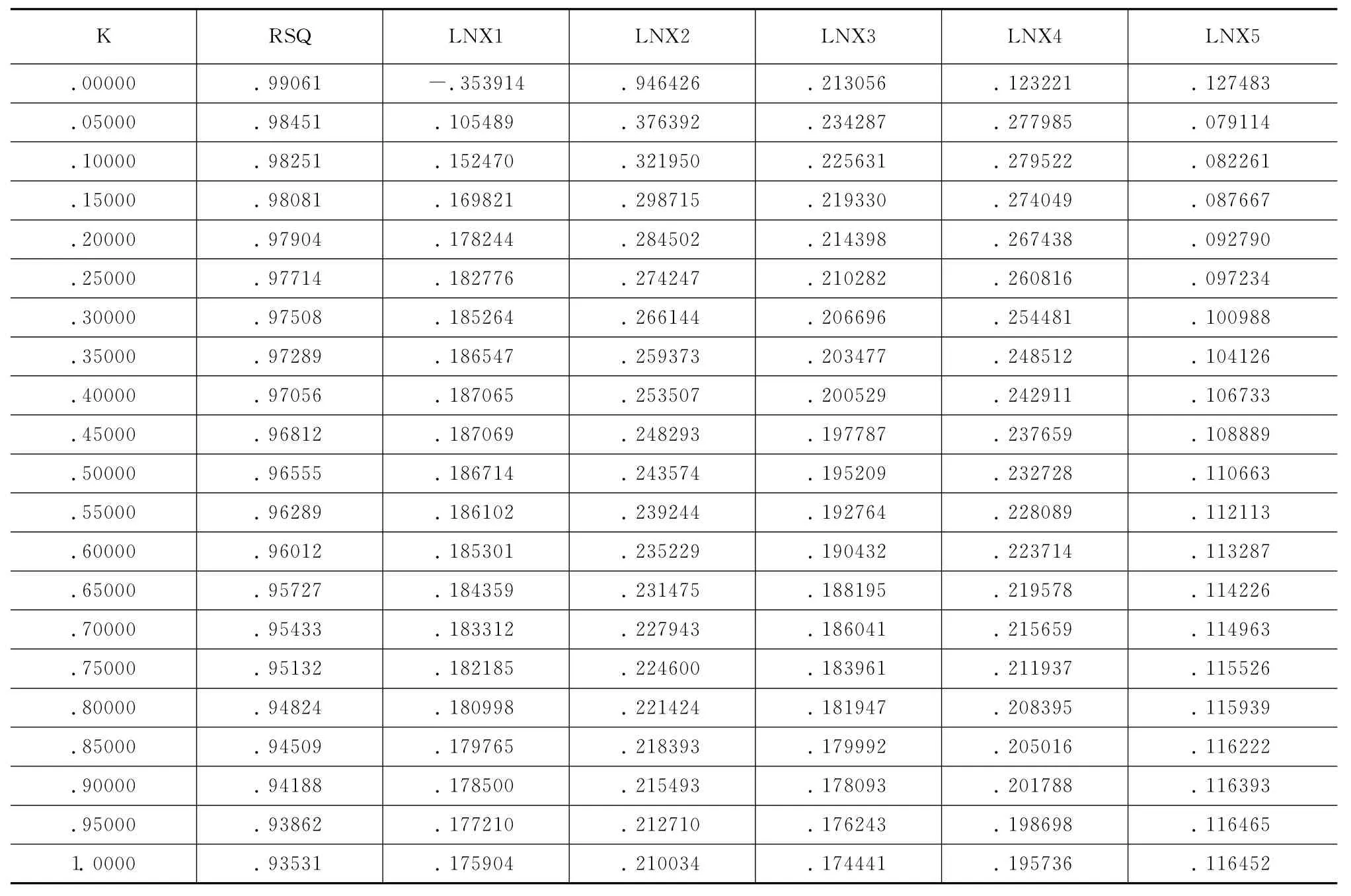
表1 岭参数K值表

从岭迹图上看，最小二乘的稳定性很差，当K稍微增大时，系数有较大的变化。对各个变量分别来看，当K＝0，LNX2、LNX3、LNX4、LNX5对于变量有显著性正的影响，LNX1对于变量有负的影响，从岭回归的角度来看，自变量LNX2，LNX3，LNX4随 K的增大其系数值迅速减小最终趋于稳定，LNX1随K的增大其系数值迅速增加最终趋于稳定，当K逐渐增大时，LNX1由负的影响迅速变为正的影响并且趋向于稳定，由此决定用5个变量做岭回归。把岭参数步长改为0.02，范围缩小到0.2，在SPSS中用命令生成得到如下结果：

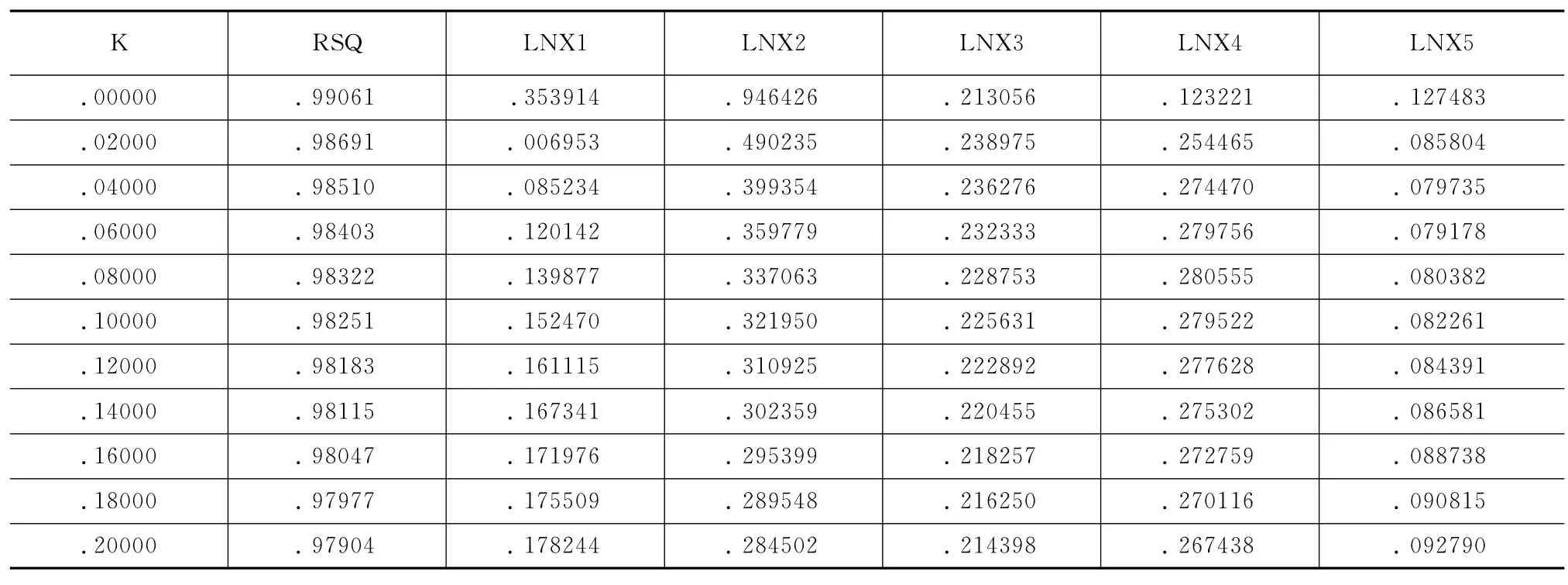
表2 调岭参数步长＝0.02后岭参数K值表

从岭参数K值表结果看，当岭参数K在0.06-0.10之间已经基本稳定，当K＝0.08时候，R2＝0.98322仍然很大，因而可以选取岭参数K＝0.08，给定K＝0.08再次做岭回归，得到输出结果如表3所示。

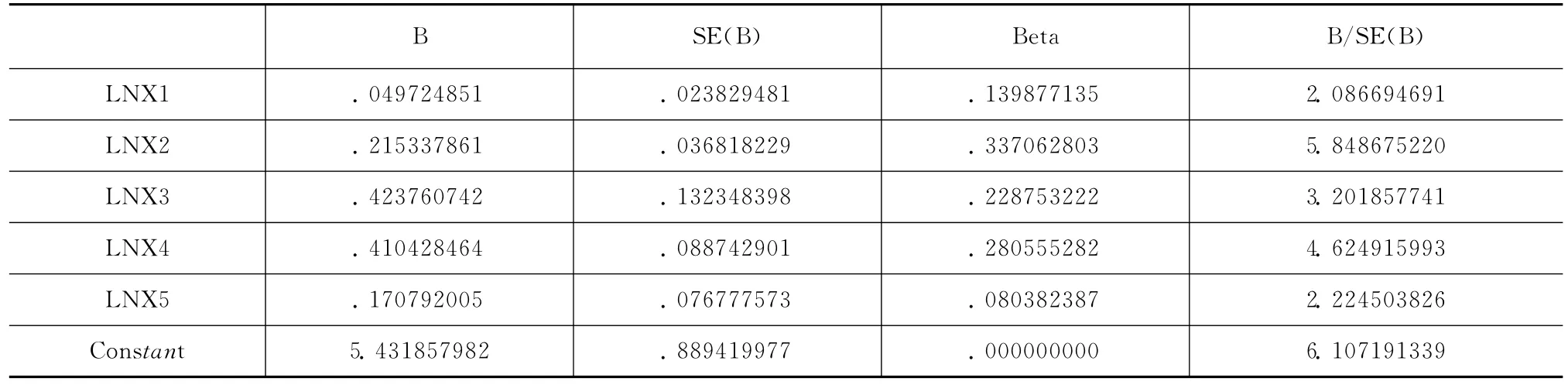
表3 K＝0.08时岭回归输出结果

由岭回归输出结果可以得到LNY对于LNX1，LNX2，LNX3，LNX4，LNX5标准化岭回归方程为：

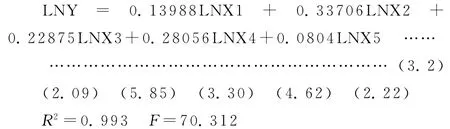
由此我们可以看出，通过标准化岭回归得到的T统计量比OLS估计显著，各个变量的系数经济意义也更加合理，可以看到各个变量对乌鲁木齐货运量不同程度的影响。

3.主成分分析法

用SPSS软件采用主成分分析法可以得到前两个因子的累积贡献率已经达到91%以上，故取因子数m＝2。提取出公共因子，为了使因子便于解释，使用方差极大法将因子旋转，采用回归法估计因子得分系数，得出函数如下：

进而可以得出，

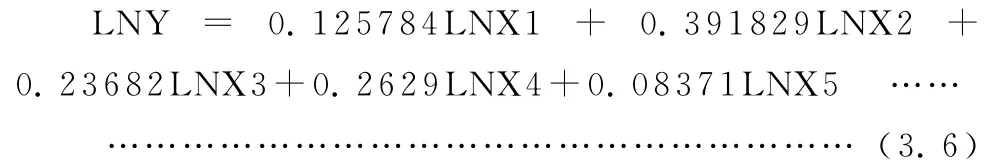
由上面的分析我们看到岭回归和主成分的所得到的结果比较接近，得出的各个系数比较简单二乘法也更加的合理，更加符合现实意义。

三、结 论

主成分分析法和岭回归法所估计的参数，都已经不是无偏的估计，主成分分析法作为多元统计分析的一种常用方法在处理多变量问题时具有其一定的优越性，其降维的优势是明显的，主成分回归方法对于一般的多重共线性问题还是适用的，尤其是对共线性较强的变量之间.岭回归法估计是通过最小二乘法的改进允许回归系数的有偏估计量存在而补救多重共线性的方法，采用它可以通过允许小的误差而换取高于无偏估计量的精度，因此它接近真实值的可能性较大，但k值的选取具有主观性，选取不当可能造成很大误差。作为统计方法，每种方法都有其适用范围，没有一种统计方法具有超过其他方法的特殊优势，在实际计量统计分析需要依据考察因变量、自变量的特点和数据特征灵活加以运用。

［1］何晓群.应用回归分析［M］.北京：中国人民大学出版社，2007.

［2］白雪梅，赵松山.更深入地认识多重共线性［J］.东北财经大学学报，2005（2）：8-12.

［3］刘罗曼.用主成分回归分析解决回归模型中复共线性问题［J］.沈阳师范大学学报：自然科学版，2008（1）：42-44.

［4］刘国旗.多重共线性的产生原因及其诊断处理［J］.合肥工业大学学报：自然科学版，2001（4）：607-610.

［5］乌鲁木齐统计局.乌鲁木齐统计年鉴2012［M］.北京：中国统计出版社，2012.