纳观纹理表面往复滑动接触磨损问题研究进展

佟瑞庭

（西北工业大学机电学院，陕西西安 710072）

可持续发展是当今世界面临的重大挑战。据估计，世界总能源的1／3被各种形式的摩擦所消耗，2006年中国在摩擦、磨损和润滑方面消耗的资金约为9 500亿元，通过正确运用摩擦学知识可以节省资金高达3 270亿元，占中国国内生产总值的1.55%［1］。可以说，摩擦磨损给现代社会造成了巨大的经济损失和能源浪费，改善接触体摩擦磨损性能对于节约能源，建设低碳型社会有着深远的意义。

摩擦磨损行为伴随着接触表面原子的迁移，随着摩擦学研究的深入进行以及微／纳机电系统的快速发展，纳米摩擦学由于能够有效研究原子尺度的摩擦磨损行为，已成为国内外学者的研究热点。凡是有相对运动的接触表面就存在摩擦与磨损。与宏观接触体相比，微／纳器件比表面 （表面积与体积的比例）迅速增大，在相对运动过程中，由于尺度效应和黏着效应的影响，磨损现象尤为严重。如：美国Sandia实验室在研制微齿轮驱动机构时发现，齿轮与凸缘之间的黏附磨损严重影响微驱动机构的性能［2］，静电微电机转子同主轴间的黏附磨损使微电机很快失效，难以应用于工程实际。雒建斌等指出，纳米尺度磨损研究是微／纳米制造中摩擦学面临的紧迫任务之一［3］。微／纳器件表面间存在严重磨损的主要原因是：在微／纳尺度，比表面急剧增大，黏着力占据主导地位。表面纹理（surface texture）技术，通过在微／纳器件表面加工纹理，可以减小表面积，降低比表面及黏着作用；另一方面，利用表面纹理的凹坑存储润滑油及磨损粒子［4-5］，对降低表面磨损有着积极的意义。然而，佟瑞庭在研究纳观黏着滑动（单次滑动）接触问题时发现，表面纹理的存在可能使基体产生微裂纹（图1a））或造成表面缺陷（图1b）），从而加剧表面磨损［6］。EDDOUMY等的试验研究也发现在往复滑动作用下，滑动方向垂直于纹理方向时，表面纹理会造成局部应力集中，使基体出现微裂纹［7］。可见，表面纹理的引入，可能会降低磨损或加剧磨损，如何合理设计纹理表面，降低微／纳器件间的表面磨损，对于提高产品寿命，实现微／纳机电系统的更广泛应用，有着重要的理论意义和应用价值。

图1 黏着滑动接触过程中出现的微裂纹及表面缺陷Fig.1 Micro-fracture and surface defect during adhesive sliding contact

由于以牛顿力学为基础的传统宏观力学已不能完全适用于纳米尺度滑动接触问题的研究，现有理论的不完善以及尺度效应的限制等，使目前纹理表面纳观磨损问题的研究主要集中于试验研究和数值模拟研究。

试验研究是随着纳米尺度实验仪器的发明而发展起来的，主要的实验设备有原子力学显微镜（atomic force microscope，AFM））、表面力仪（surface forces apparatus，SFA）、扫描隧道显微镜（scanning tunneling microscope，STM）、纳米硬度计（nano indenter）、纳米划痕仪（nano scratch tester）以及纳米摩擦试验机（nano tribometer）等。上述实验设备对纳观滑动接触的研究起到了推动性的作用，并已取得大量成果［8-13］。然而，试验结果往往由于试件表面被污染或表面本身存在缺陷以及一些不确定性因素的影响而失真［14］。数值模拟研究则可以避免其他因素的干扰，针对某个或某几个具体因素进行研究。

纳米尺度的数值模拟并存3种方法［15］：量子力学方法，分子动力学方法，连续介质力学方法。然而，在数值模拟方法的应用方面，量子力学方法仅适用于100个原子以下的系统，计算规模极为有限，无法达到纳观接触问题的模拟要求。分子动力学方法存在固有的局限性［16］：1）所计算的空间和时间尺度有限；2）边界条件的等效处理；连续介质力学方法以偏微分方程的形式描述各守恒定律及材料的本构关系，尽管已广泛应用于固体力学、流体力学等领域，并解决了大量的工程实际问题，但当接触模型的尺寸减小到纳米尺度，由于其只考虑材料的物理、力学特性均匀化行为，而不能观察接触过程中原子尺度的物理力学行为（如纳米器件的表面黏着现象、内部缺陷等），因此在纳观接触力学的研究中不再适用［17］。加州大学Berkeley分校的KOMVOPOULOS指出，在接触力学中提出对不同尺度都有效的多尺度模型是必要的［18］。因此，如何在研究原子尺度的行为细节的同时，又兼顾模拟规模，已成为一个热门课题。目前，一种可行的方案是，在发生原子尺度行为的区域采用分子动力学方法，而在周围区域或远离区域采用连续介质力学方法，如有限元方法、无网格方法等。这样既能节约计算成本，又能保证所研究问题的物理特性。近10年来，很多此类耦合方法（或称为多尺度方法）应运而生［19-21］，从而为纳观纹理表面往复滑动接触磨损问题的研究提供了强有力的手段。

本文对纳观纹理表面往复滑动接触磨损问题的试验研究和数值模拟研究进行了综述，介绍了纳观纹理表面往复滑动接触磨损问题试验研究相关成果，分析了试验研究可能存在的问题，进一步阐述了纳观纹理表面往复滑动接触问题的数值模拟研究进展，并给出了多尺度方法模拟该问题的算例。最后，探讨了该问题未来可能的发展方向和趋势。

1 试验研究

以以色列学者ETSION为代表，国内外学者进行了大量的试验研究，并取得了许多重要成果［22］。MITCHELL等研究了微纹理表面的单向和往复滑动摩擦行为［23］。对于单向滑动试验，较大尺寸的凹坑或柱状纹理表面，可以获得较低的摩擦系数。文中还指出，单次滑动测试所得的摩擦系数不能用于预测往复滑动稳定状态后的摩擦系数。SINGH等的研究发现，微／纳尺度的Si（100）纹理表面可以提高摩擦性能［24］。同时，在试件上出现了磨损粒子，磨损粒子的存在同样会影响摩擦行为。表面纹理的引入，可以存储磨损粒子或润滑油，将会对进一步滑动过程产生积极的影响。

MENEZES等采用Al-4Mg合金探针在钢盘上往复滑动并进行摩擦性能测试［25］。钢盘试件表面加工分别有单向纹理、8字形纹理和随机纹理。对于单向纹理和8字形纹理，摩擦系数随滑动次数的增加而降低，而随机纹理则呈现出相反趋势。GARRIDO等采用AISI 416不锈钢探针对NiCrBSi激光纹理表面进行往复滑动试验［26］。试验结果表明，凹坑直径较小时，纹理表面可以有效改善摩擦性能，而不恰当的凹坑密度会造成纹理表面的破坏。PODGORNIK等结合试验研究和数值分析，研究了纹理表面在不同润滑机制下的作用［27］。对于贫油润滑，纹理表面会导致摩擦力增大；对于边界润滑，较小的凹坑以及具有较小凹坑密度的纹理表面能够降低摩擦；在全油润滑状态下，较大深度的凹坑纹理表面呈现出低摩擦水平。WANG等利用摩擦试验机研究了Ni纳米颗粒纹理表面（NDPS）的摩擦行为［28］。结果表明，与之相配发生相对滑动的凸峰尺寸影响接触面积和接触压力，并进一步影响摩擦系数。与纳米颗粒的间距相比，当凸峰尺寸相对较大时，NDPS才能降低摩擦。RAMESH等研究了不锈钢纹理表面往复滑动摩擦性能，发现与无纹理表面相比，纹理表面能够使摩擦力降低80%［29］。KOVALCHENKO等的研究指出，尽管激光纹理表面（LST）能够降低摩擦，但LST在某些情况下会增大与之接触表面的磨损和接触压力［30］。PETTERSSON等在活塞表面加工平行和交叉的凹槽，通过往复滑动试验研究表明，在初始阶段，所有的纹理表面均能降低摩擦系数，随着滑动接触的进行，差别很快变小［31］。

AYALA等通过AFM研究了氟化碳膜的磨损特性［32］。试验结果表明，磨损痕迹与膜的硬度直接相关，但硬度不是衡量纳观磨损的唯一参数，表面凸峰的分布情况以及膜材料的弹性模量等同样会影响磨损性能。GRAÇA等的研究表明，磨损体积与外加载荷及相互作用次数成正比。表面粗糙度会影响接触凸峰的局部塑性变形，在磨损的萌发阶段起着非常重要的作用。凸峰的变形引起磨损的萌发，最终导致材料剥落［33］。ACHANTA等的研究也指出，凸峰在往复载荷作用下会产生过大应力，导致凸峰断裂，生成磨损粒子，而磨损粒子可以填充凸峰间的空隙，使表面粗糙度减小，有效降低磨损［34］。CHOUQUET等在DLC（类金刚石）涂层表面上加工不同直径、不同深度的圆孔形成纹理表面，并试验研究了钢球与此类纹理表面的滑动摩擦磨损性能［35］。通过磨损轨迹的研究，发现相对无纹理表面，纹理表面均能够在不同程度上降低磨损，并进一步指出，接触直径与圆孔直径的比率是一个非常重要的参数，需要更加深入的研究。

在中国，温诗铸院士于1998年撰写专著《纳米摩擦学》并率先开展纳米尺度摩擦磨损相关研究。张晓亮等在单晶硅（100）面上制备Au纳米颗粒织构化表面（textured surface），并利用AFM和摩擦磨损试验机研究了该织构化表面的摩擦性能，发现摩擦对偶曲率半径远大于颗粒曲率半径及颗粒间隙时，耐磨寿命随颗粒堆积密度的增大而延长［36］。吕文斐等在45＃钢表面制备点状、槽状和网格状形貌纹理，与SiC钢球配副，在石蜡和机油润滑条件下进行往复摩擦试验，发现网格状形貌试样相对于点状和槽状形貌试样具有更小的摩擦系数和更好的耐磨性［37］。LI等在Ni基复合材料上加工了3种不同密度的微孔，并在微孔中填充MoS2作为润滑剂，进行球体与纹理表面的磨损试验，结果表明微孔密度为7.1%时，可获得低磨损率及长磨损寿命［38］。朱华等的研究则指出，变密度织构在改善往复运动摩擦副的摩擦性能方面有很大潜力［39］。刘一静等在活塞裙部表面制作了不同直径、不同深度的表面织构，并在往复式摩擦磨损试验机上进行试验，结果表明：文中采用的表面织构，在活塞／缸套摩擦过程中能够起到明显的减摩降磨作用［40］。

除表面凸峰分布或表面纹理／织构相关因素外，其他因素如外加载荷、滑动速度、滑动方向、探针半径以及润滑条件等也会影响接触体的磨损性能。JIANG等应用点接触显微镜在金薄膜上的纳米磨损试验研究指出，试验条件对试验结果有较大影响：在相同作用条件下，磨损深度随载荷的增加而增大，随扫描次数的增加而线性增大，随扫描间距的增大而减小，且锋利（较小半径）探针作用下的磨损深度较大［41］。MARUI等通过探针与圆盘的单向摩擦以及探针与大平面往复运动的磨损试验研究了摩擦形式对磨损的影响。发现探针向右滑动时的摩擦力略大于向左滑动时的摩擦力（探针先向右滑动，后向左滑动）。由于探针的材料为铜，容易变形，因此2种摩擦形式的磨损率差别较小［42］。BONNY等的往复滑动接触试验研究表明，磨损量随外加载荷的增大而增大，随滑动速度的增加而增大［43］。DENG等在超硬合金刀具表面加工微孔，以MoS2为润滑剂，进行切削试验，与无微孔表面相比，切削速度较低时，带微孔刀具的切削力、摩擦系数均有较大幅度降低，且刀具的磨损量较小［44］。胡天昌等利用激光对GCr15钢表面进行微坑织构化处理，探讨了激光表面织构对摩擦磨损性能的影响。与光滑表面相比，织构化表面在干摩擦条件下出现高摩擦系数，但有较好的抗磨性能。而贫油条件下，织构表面能够有效减摩降磨［45］。解国新等利用AFM研究了十八烷基三氯硅烷（OTS）分子润滑膜对硅表面摩擦磨损性能的影响，指出OTS润滑膜可以大大提高微／纳机电系统的可靠性，延长其使用寿命［46］。

尽管试验研究的较多成果已应用于工程实际，但纳观纹理表面往复滑动接触磨损试验复杂耗时，且对仪器设备的损耗严重，使得时间与设备成本激增。磨损过程对材料的局部压缩和剪切作用，使其容易发生塑性变形，产生微裂纹或造成粒子脱落等，由于粒子的不断迁移，伴随着接触界面的不断更新，使得接触条件持续改变。尽管采用全息显微镜可以在线观测滑动接触表面的状况［47］，但试验设备很难跟踪微裂纹的扩展、位错的移动等，也很难研究其对磨损过程的影响。数值模拟方法则提供了一个有效的解决方案，既可以降低研究成本，又能够实时观测或再现微裂纹的萌生、扩展，位错的移动等，尤其适用于往复滑动接触纳观磨损过程多变现象的研究。

2 数值模拟研究

数值模拟研究方面，由于传统的连续介质力学方法，无法建立磨损体积与滑动速度等之间的相互关系，无法考虑材料硬度与接触尺度的相关性［33］，已不能应用于纳观磨损研究。而分子动力学（molecular dynamics，MD）模拟能够兼顾上述问题，因此在纳观磨损问题的研究中得到广泛应用。多尺度方法将分子动力学与连续介质力学方法耦合，在需要关注原子行为细节的区域采用MD模拟，而在其他区域采用连续介质力学方法求解，继承了MD模拟分子／原子间相互作用的优势，又能够节约计算耗费，近年来得到越来越多的重视。

2.1 分子动力学模拟

ZHANG等应用MD模拟研究了金刚石-铜滑动系统的磨损机理，指出滑动过程存在4种磨损形式［48］：1）无磨损形式；2）黏着磨损形式；3）犁沟形式；4）切削形式。这些形式由关键滑动参数如滑动速度、润滑条件等控制。YUE等对纳米孪晶、纳米晶粒以及纳米单晶铜磨损引起的缺陷产生过程的MD模拟指出，单向滑动与双向滑动会对磨损过程造成不同的影响［49］，这与MARUI等的试验结果类似［42］。在中国，林滨等应用MD模拟了纳米磨削过程，发现摩擦力的波动与位错滑移和晶格塑性变形的产生有关［50］。张俊杰等对单晶铜AFM加工过程的MD模拟指出，工件材料的晶向和切削方向对亚表面变形层有显著影响［51］。朱朋哲对纳米刻画过程犁沟和黏着摩擦的MD模拟表明，切削摩擦系数占总摩擦系数的17%～31%［52］。除此之外，还有很多学者如重庆大学的段芳莉、大连理工大学的郭晓光以及大连海事大学的程东、严志军等在MD模拟纳米尺度摩擦、磨损或切削方面进行了大量相关研究，其文献不再一一列举。由于MD模拟过程计算耗费严重，上述数值模拟研究主要讨论单次滑动后的结果，对往复滑动接触时的纳观磨损问题及纳观纹理表面的磨损问题研究较少。然而，单次或较少次数的滑动接触，很难反应往复滑动接触磨损的实际工况。一方面，往复滑动过程中，随着滑动次数的增加，纳米尺度材料的硬度发生变化［33］，而硬度是影响磨损过程的重要参数。另一方面，磨损过程存在一个磨合期［33-34］，往复滑动作用下，表面会在较低的接触应力下发生磨损。此外，单次或较少次数的滑动过程无法体现磨损粒子在进一步滑动接触过程中的角色，也无法研究前期滑动产生的微裂纹、表面缺陷等对进一步磨损造成的影响。MD模拟的计算耗费与往复滑动接触磨损研究的需求之间的矛盾，使得发展快速有效的MD模拟算法成为解决上述问题的重要环节。

INAMURA等先后提出了重构分子动力学和重构组合分子动力学方法，将模拟区域用包含若干原子的原子簇代替，能够极大节约计算时间，但原子簇内部不能出现缺陷［53］。LIU等提出的光滑分子动力学方法，能在一定程度上节约计算时间，但尚未有将该方法应用于纳观磨损问题的报道［54］。MAEKAWA等提出了面积约束分子动力学（area-restricted molecular dynamics，ARMD）方法，用于降低纳米尺度加工过程磨损问题模拟的计算耗费。该方法可以获得与传统全规模MD模拟相同的结果，但并未展开对三维问题的研究［55］。另外，为了节约计算成本，应用MD模拟纳观磨损问题时，经常采用较高的滑动速度，如文献［48］的20，100，200m／s，文献［53］的200m／s等，而YANG等的研究指出，高速滑动会导致结果振荡失真，采用低速滑动更贴近于工程实际［56］。

2.2 多尺度方法

多尺度耦合方法并不是一个全新的领域，它的根源要追溯到20世纪70年代，文献［57］—文献［59］中，应用连续弹性体为原子区域提供边界条件，SINCLAIR用解析方法处理连续介质区域，允许在原子区域的能量最小化过程中修改边界条件［59］。可以说，文献［59］的工作开创了多尺度耦合方法的先河。到了20世纪80年代，MULLINS等在耦合方法中开始采用有限元方法对连续介质区域建模［60-61］。KOHLHOFF等对MULLINS等的方法进行了改进，采用非局部弹性理论描述原子与有限元耦合区域，并对体心立方晶体的裂纹扩展进行了研究［62］。然而，上述方法中对原子区域未能采用分子动力学模拟，且主要用于裂纹扩展的研究。与现在的计算水平相比，模拟规模较小，如SINCLAIR在文献［59］中应用924个原子研究了裂纹扩展，而文献［61］中原子区域则仅含有236个原子。

分子动力学与连续介质力学方法的耦合，起始于20世纪90年代末期。RUDD等提出了一种粗晶粒分子动力学（coarse-grained molecular dynamics，CGMD）方法，通过构造适用于原子尺度网格的尺度相关本构方程，实现了分子动力学与有限元方法的耦合，尽管只用于一维问题的求解，但在该领域迈出了重要的一步［63］。SMIRNOVA等的多尺度方法是在分子动力学与有限元方法耦合处原子与有限元节点位置重合，应用该方法对固体中激光感应应力波的传播问题进行了研究，与全分子动力学方法所得结果相比，误差仅为5%［64］。

CAI等提出了格林函数（Green function）方法，动态耦合2个区域［65］。这一方法成功的对边界波反射问题进行最小化处理。然而，该方法需要在边界处精确计算线性响应函数，其矩阵形式的大小与原子区域边界处的自由度相等，由分子动力学模拟计算所得。因此该方法尽管很精确，但需要大量的计算时间。E和HUANG在原子区域与连续介质叠加区域给出了一组匹配条件，通过构建时间积分公式去除边界伪反射，保证信息传递的精确性［66-67］。该方法是在“吸收边界条件”［68］的基础上发展起来的，通过修改界面附近原子的运动控制方程，吸收界面处的高频波，而只保留低频波。DEYMIER等提出了一种基于格林函数的方法，用于计算并发弹性多尺度模型的动态特性［69］。该方法的研究表明，在高频时，原子区域弹性波能量在传递过程中被严重减缓，因此，此方法只适用于波长较长的情况。MURALIDHARAN等的多尺度方法在弹性连续介质区域采用时域有限差分方法，而在原子区域采用分子动力学方法，连接域包含了空间尺度和时间尺度的耦合［70］。文中检验了弹性波在界面处的反射，结果显示界面处只有一小部分波反射，从而验证了耦合方法的有效性。连续介质区域的离散化程度对该区域的频率特性强加了一个限制，可能导致分子动力学区域周围产生局部共振现象。SHENOY等提出的动态准连续介质（quasicontinuum，QC）方法用于温度为零时纳米压痕与裂纹扩展的动态模拟［71-72］。通过引入LESAR等提出的局部准谐波模型计算原子区域的自由能［73］。然而，对于不均匀的网格划分，QC方法受到非物理波反射的困扰。CURTAROLO等提出了一种属于重整化群理论（renormalization group theory）的方法，引入了与时间重整化相关的动态指数，建立了一种新的节点局部能量模型［74］。该方法在二维问题中进行验证，动态网格稀疏化未能解决原子区域与连续介质区域的热传递，但使界面处的热阻达到了最小化。BELYTSCHKO等提出了桥域方法（bridging domain method）［75-76］。其原理在文献［75］中有详细的介绍：假设有限元解与分子动力学解在整个区域同时存在，分子动力学计算只在必要的区域进行，细微尺度和稀疏尺度在叠加区域内通过拉格朗日乘子进行连接。该方法在每个时间步，将桥域内的细微尺度解投影到稀疏尺度解，从而滤掉界面处的高频部分。另外，此方法并非基于线性化假设，因此可以应用到非线性问题的求解。WAGNER等、PARK等提出的桥尺度方法（bridging scale method，BSM）通过在多尺度边界引入时间历程因子确定边界处虚原子（ghost atoms）的位移，从而实现尺度间物理信息的光滑传递［77-85］。

SHILKROT等和 MILLER等提出的耦合原子离散位错（coupled atomistic／discrete dislocation，CADD）方法，允许连续介质区域发生位错等行为，可以有效解决材料非弹性变形以及塑性流动问题，并能够实现位错由原子区域向连续介质区域传递，这是上述其他方法所不能实现的［86-89］。因此，该方法在纳米压痕中得到了广泛应用。QU等提出了动力学有限温度耦合方法［90］，在CADD方法中引入“阶段阻尼（stadium damping）”的思想［91］，用于吸收耦合界面处的高能脉冲。该方法在边界区域的原子运动方程中插入了附加的朗之万（Langevin）阻尼项，对固定温度下原子内部区域的平衡以及吸收原子区域产生的向耦合界面处移动的弹性脉冲方面有很好的前景。SHIARI等改进了CADD方法，使其不再局限于零温度的情况，并应用该方法研究了压痕过程与温度、速率的关系［92］。该方法可以实现位错生成、原子运动的可视化及量化，包括由位错导致的表面变形的演化等。LUAN等在CADD方法的基础上提出了混合多尺度方法，通过位移边界条件将分子动力学与有限元交叠区域耦合起来，实现物理量在两区域的有效传递［93］。与全分子动力学模拟相比，接触面积、压力分布、静态与动态摩擦力等计算结果基本一致，而计算时间仅为原来的1／20。

多尺度方法的另一条实现途径是边界条件的施加。PARK等提出了一套适合于分子动力学方法、连续介质力学方法以及多尺度耦合方法的无反射边界条件的计算方法［94］。该方法假设区域边界附近的载荷可以由位移的线性函数表示，利用标准的Laplace和Fourier变换技术消除不必要的自由度。LIU等和KARPOV等提出了一种不需要连接域的半解析多尺度边界条件方法，通过离散Fourier变换生成用离散卷积算子表示的紧支公式，实现位移沿着密化-稀疏尺度边界的耦合，避免了由于连续介质区域节点在连接域骤然密化而生成病态刚度矩阵［95-97］。该方法与全分子动力学模拟比较，计算结果较为吻合，而计算耗费仅为全分子动力学的1／8。在中国，有关学者从不同角度提出了多尺度方法及模型［98-101］。

由于多尺度方法相对分子动力学方法能节约大量计算时间，又能进行原子行为细节的研究，使得其在裂纹扩展、纳米压痕以及纳米摩擦学等领域显示出巨大的潜力，业已得到广泛应用。

综上所述，纳观纹理表面往复滑动接触试验研究能够提供第一手资料，但其需要较高的成本，且受到仪器设备和试件的限制，难以考虑多因素对摩擦磨损性能的综合作用。试验过程中，采用传统设备很难实时监测接触体内部的原子运动细节行为，也无法研究材料内部微裂纹的扩展、位错的移动以及可能存在的缺陷等对摩擦磨损过程的影响。另外，试验设备刀具或探针的磨损很难量化，因此对试件磨损量的测量会存在一定的误差，从而影响整个研究过程。数值模拟研究方面，分子动力学模拟技术能够描述原子间作用过程，并可通过数据后处理实现作用过程的在线演示，已成功运用于纳观滑动接触问题的研究。分子动力学模拟过程中，每次加载后要计算原子间相互作用，并经过弛豫平衡后才能进行下一步加载，计算成本高，很难将其应用于往复滑动接触问题的研究。多尺度方法采用分子动力学与连续介质力学方法耦合技术，融合了分子动力学在原子尺度行为研究的能力以及连续介质力学方法在计算时间上的优势，既兼顾计算规模，又能够节约计算成本，尤其适用于纳观纹理表面往复滑动接触磨损问题的研究。

3 多尺度方法模拟往复滑动接触问题算例

图2所示为二维刚性圆柱压头与纳观纹理表面的往复滑动接触多尺度模型。圆柱压头由4层原子组成，共120个原子，压头半径为R=30r0，其中，r0是Lennard-Jones参数。对于本文采用的单晶铜，r0=0.227 7nm［102］。基体划分为2部分：分子动力学区域（MD region）和有限元区域（FE region）。对于MD区域，除表面纹理外，由31层原子组成，每层包含113个原子，共有3 503个原子。定义x方向上的2个原子之间的距离为dx（dx=21／6r0），y方向上两层原子之间的距离为dy（dy=31／2／2×dx），则 MD 区域的尺寸为112.5dx×30.0dy。将FE区域离散为三角形有限单元，共包含102个有限元节点和162个三角形单元。FE区域的尺寸为112.5dx×56.0dy。MD区域与FE区域的叠加区域的尺寸为112.5dx×6.0dy。因此，基体的总体尺寸为112.5dx×80.0dy。刚性圆柱压头与基体的初始间隙为dg=2.5r0。压头下方的凸峰定义为“1号凸峰（1stasperity）”、“2号凸峰（2ndasperity）”、…、“7号凸峰（7thasperity）”。

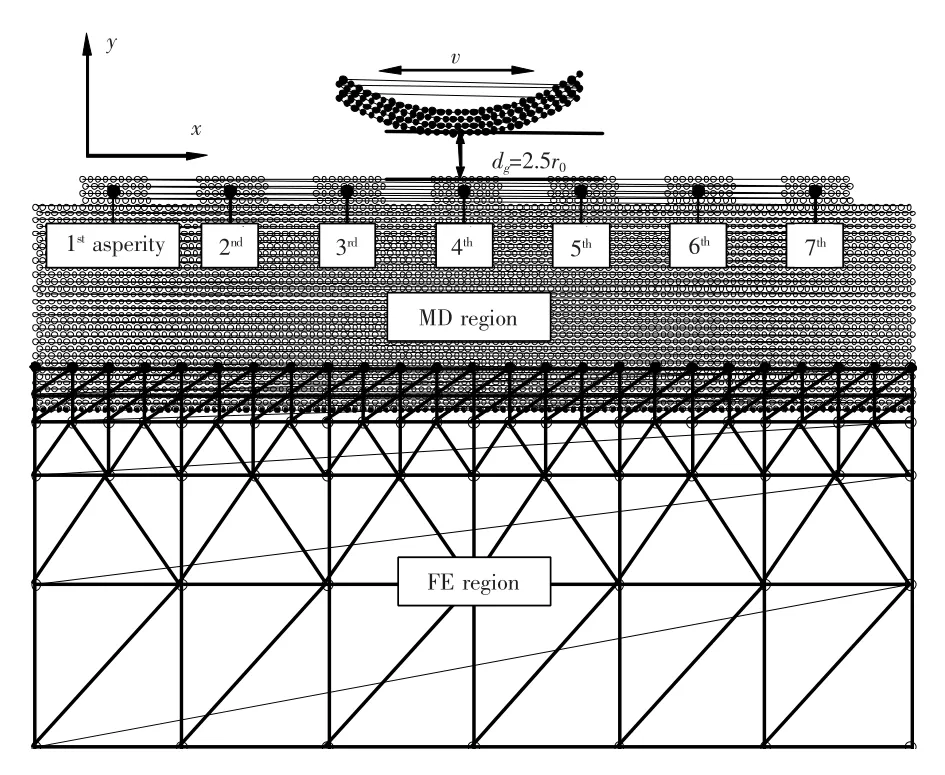
图2 二维纹理表面往复滑动接触多尺度模型Fig.2 Two dimensional multiscale model of reciprocating sliding contact between textured surface

图3 纹理表面及其参数Fig.3 Textured surfaces and their parameters

图3给出了本文设计的4种不同凸峰形状的纹理表面，尺寸参数为凸峰宽度a=8dx，凸峰间距b=7dx以及凸峰高度h=4dy。4种纹理表面分别命名为“表面Ⅰ（surfaceⅠ）”、“表面Ⅱ（surfaceⅡ）”、“表面Ⅲ（surfaceⅢ）”和“表面Ⅳ（surfaceⅣ）”。对于表面Ⅰ，每个凸峰每层原子的个数为mA=9。对于表面Ⅱ，每个凸峰从底层原子到顶层原子的个数分别为mA=9，8，7，6。在表面Ⅲ和表面Ⅳ中，mA=9，9，8，8。4种纹理表面上凸峰个数均为nA=7。

多尺度模拟过程中，对MD区域进行分子动力学模拟，采用经典的Lennard-Jones两体势描述基体原子之间以及接触问题中压头与基体原子之间的作用，采用Velocity-Verlet算法［103］计算原子的坐标、速度以及加速度，固定时间步为Δt=0.95fs。最初，除底层以及左右边界原子固定外，其他原子的速度设置为一个固定值vo，vo取决于系统温度，其中T=300K，为系统温度，N为原子总数。压头下压前，基体经过12 000Δt的弛豫时间后达到相对平衡状态。模拟过程中刚性压头下压趋进增量为Δs=0.05r0，每次加载后的弛豫时间为6 000Δt，压头下压速度为v=2.0m／s，下压深度为d=2.5r0。分子动力学每迭代50步进行一次有限元计算。下压完成后，压头先向右滑动（对应奇数滑动次数）320Δs，然后再向左滑动（对应偶数滑动次数）320Δs。如此向右向左反复滑动10次。

图4给出了4种纹理表面每次滑动过程的平均势能和平均摩擦力。

图4a）中，对于所示20次滑动过程，平均势能和平均摩擦力均未达到稳定值。根据表面Ⅰ滑动过程参数驱动的动画演示，基体表面的原子在压头的作用下一直发生迁移，表面形貌始终未能保持稳定结构，说明刚性压头与表面Ⅰ的滑动接触尚处于“磨合”阶段。

图4b）给出的是刚性压头与表面Ⅱ滑动接触过程中的平均势能和平均摩擦力。从第11次滑动开始，压头携带一些原子在一个大凸峰上平稳滑动，平均势能也处于稳定状态。大凸峰是由4号和5号凸峰在压头的作用下形成的，这2个凸峰的部分原子吸附于压头表面，此后提到的压头均包含吸附于其表面的基体原子。稳定滑动阶段，压头向右滑动（奇数）时，大凸峰左半部分对压头的吸引力方向与滑动方向相反，与摩擦力方向相同，而当压头向左滑动（偶数）时，该方向与滑动方向相同，与摩擦力方向相反，因此向右滑动时的平均摩擦力大于向左滑动时的平均摩擦力。往复滑动接触过程从第11次滑动开始进入稳定阶段，且其平均摩擦力与初始滑动阶段相比有较大幅度降低，说明表面Ⅱ有利于降低摩擦或磨损。

对于表面Ⅲ，从第13次滑动开始，平均势能保持在稳定值，平均摩擦力也开始规律变化（向右或向左滑动的平均摩擦力保持稳定），如图4c）所示，说明此时滑动接触过程进入了稳定状态。在接下来的滑动接触过程中，奇数滑动（向右）的平均摩擦力小于偶数滑动（向左）的平均摩擦力。这一现象是由6号凸峰对压头的吸引力造成的。压头向右滑动时，6号凸峰对压头的吸引力方向与滑动方向一致，与摩擦力方向相反，而当压头向左滑动时，吸引力方向与摩擦力方向相同，因此向右滑动（奇数）的平均摩擦力小于向左滑动（偶数）的平均摩擦力。尽管表面Ⅲ也进入了稳定滑动过程，但其稳定阶段压头向左滑动时未能有效降低平均摩擦力，因此表面Ⅲ不能用于降低摩擦力。由动画演示可知，表面Ⅲ的磨损粒子数与表面Ⅱ相当，其磨损性能也与表面Ⅱ相当。

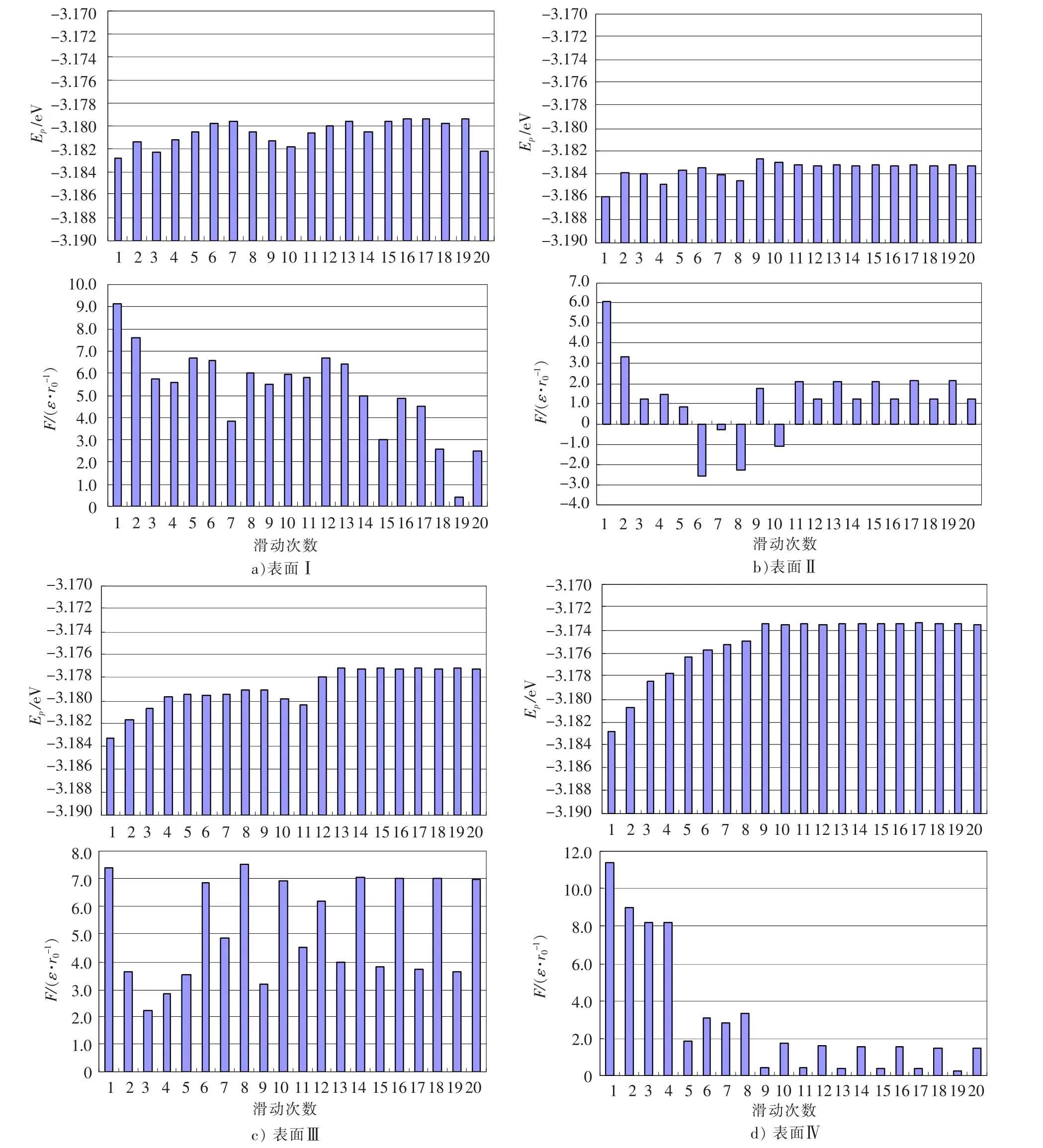
图4 每次滑动过程的平均势能和平均摩擦力Fig.4 Average potential energies and friction forces of each sliding contact process

对于表面Ⅳ，“磨合”阶段仅持续了8次滑动，如图4d）所示。在第8次滑动过程中，吸附在压头表面的一层原子被分割为2部分：左半部分和右半部分。左半部分与基体没有发生接触，相互作用也较小。因此，右半部分与基体的作用在接下来的滑动过程中起着重要的作用。对于奇数滑动（向右）过程，压头携带右半部分在基体上滑动，基体对压头的吸引力方向与滑动方向相同，与摩擦力方向相反，因此平均摩擦力较低。对于偶数滑动（向左）过程，吸引力与滑动方向相反，与摩擦力方向相同，平均摩擦力较高。表面Ⅳ的“磨合”阶段持续滑动次数小于其他3种纹理表面，表明其更容易进入稳定摩擦磨损状态。

4 结 语

从试验研究和数值模拟研究两方面介绍了纳观纹理表面往复滑动接触磨损问题的研究进展，探讨了滑动接触过程中压头的相关参数、纹理表面的相关参数以及外界其他因素对滑动接触性能的影响规律。最后，给出了利用多尺度方法求解纳观纹理表面滑动接触问题的算例。

纳观纹理表面的往复滑动接触过程是一个极其复杂的过程，它受到电场、磁场甚至声场等多场耦合作用，因此纳米尺度的试验研究面临着严峻的考验。发展大规模数值模拟算法是实现摩擦磨损精确计算和预测的重要内容之一。一旦数值模拟规模得以解决，大规模的数值模拟成为现实，使得纹理表面对滑动摩擦磨损性能的影响研究更贴近于实际工况，从而为普适性结论的提出奠定基础。研究纹理表面滑动过程中诸多相关参数对摩擦磨损性能的影响规律，是数值模拟的研究方向之一。滑动过程中粒子的剥落导致材料的磨损，模拟规模的增大也将为更深入理解摩擦磨损机理，有效改善摩擦磨损状况提供必要条件。通过表面纹理主动设计、润滑剂的设计选择、接触体材料的配对以及仿生学的应用等，实现摩擦磨损性能的主动控制，将成为今后的研究热点。

／References：

［1］ 国家自然科学基金委员会工程与材料科学部.机械工程学科发展战略报告（2011-2020）［R］.北京：科学出版社，2010.Department of Engineering and Material Science of National Natural Science Foundation of China.Development Strategy Report of Mechanical Engineering（2011-2020）［R］.Beijing：Science Press，2010.

［2］ REDMOND J M，REED J R E D，HEINSTEIN M W，et al.Microscale Modeling and Simulation［R］.［S.l］：Sandia National Labs，2001.

［3］ 雒建斌，何 雨，温诗铸，等.微／纳米制造技术的摩擦学挑战［J］.摩擦学学报，2005，25（3）：283-288.LUO Jianbin，HE Yu，WEN Shizhu，et al.Challenges to tribology arisen from the development of micro-and nano-manufacturing technology［J］.Tribology，2005，25（3）：283-288.

［4］ PETTERSSON U，JACOBSON S.Friction and wear properties of micro textured DLC coated surfaces in boundary lubricated sliding［J］.Tribology Letters，2004，17（3）：553-559.

［5］ SUH A Y，LEE S C，POLYCARPOU A A.Adhesion and friction evaluation of textured slider surfaces in ultra-low flying head-disk interfaces［J］.Tribology Letters，2004，17（4）：739-749.

［6］ 佟瑞庭.纳观黏着滑动接触的多尺度耦合方法研究［D］.西安：西北工业大学，2010.TONG Ruiting.A Multiscale Method for Nanoscale Adhesive Sliding Contacts［D］.Xi′an：Northwestern Polytechnical University，2010.

［7］ EDDOUMY F，ADDIEGO F，CELIS J P，et al.Reciprocating sliding of uniaxially-stretched ultra-high molecular weight polyethylene for medical device applications［J］.Wear，2011，272（1）：50-61.

［8］ HOH J H，REVEL J P，HANSMA P K.Tip-sample interactions in atomic force microscopy（I）：Modulating adhesion between silicon nitride and glass［J］.Nanotechnology，1991，2（3）：119-122.

［9］ ERTS D，LÓHMUS A，LÓHMUS R，et al.Force interactions and adhesion of gold contacts using a combined atomic force microscope and transmission electron microscope［J］.Applied Surface Science，2002，188：460-466.

［10］ GRYBOS J，PYKA-FOSCIAK G，LEBED K，et al.Study of adhesion interaction using atomic force microscopy［J］.ACTA Physica Polonica A，2004，105（5）：501-510.

［11］ CUENOT S，FRETIGNY C，DEMOUSTIER-CHAMPAGNE S，et al.Surface tension effect on the mechanical properties of nanomaterials measured by atomic force microscopy［J］.Physical Review B，2004，69（16）：5 410-5 414.

［12］ VANLANDINGHAM M R，JULIANO T F，HAGON M J.Measuring tip shape for instrumented indentation using atomic force microscopy［J］.Measurement Science and Technology，2005，16（11）：2 173-2 185.

［13］ KIM D.Study of friction and adhesion by atomic force microscope and their relationship to surface energy for the lubricated disk［J］.IEEE Transactions on Magnetics，2008，44（11）：4 537-4 540.

［14］ HU S Q，RAMAN A.Chaos in atomic force microscopy［J］.Physical Review Letters，2006，96（3）：6 107-6 110.

［15］ 杨 卫，马新玲，王洪涛，等.纳米力学进展［J］.力学进展，2002，32（2）：161-174.YANG Wei，MA Xinling，WANG Hongtao，et al.Advances in nanomechanics［J］.Advances in Mechanics，2002，32（2）：161-174.

［16］ LIU W K，KARPOV E G，ZHANG S，et al.An introduction to computational nanomechanics and materials［J］.Computer Methods in Applied Mechanics and Engineering，2004，193（17-20）：1 529-1 578.

［17］ LUAN B，ROBBINS M O.The breakdown of continuum models for mechanical contacts［J］.Nature，2005，435：929-932.

［18］ KOMVOPOULOS K.Scale effects on contact deformation of elastic-plastic solids［A］.Proceeding of World Tribology CongressⅢ［C］.Washington D C：［s.n.］，2005.419-426.

［19］ CURTIN W A，MILLER R E.Atomistic／Continuum coupling in computational materials science［J］.Modelling and Simulation in Mate-rials Science and Engineering，2003，11（3）：33-68.

［20］ 刘 更，刘天祥，温诗铸.微／纳尺度接触问题计算方法研究进展［J］.力学进展，2008，38（5）：521-544.LIU Geng，LIU Tianxiang，WEN Shizhu.Advances on numerical methods for micro／nano-scale contact mechanics［J］.Advances in Mechanics，2008，38（5）：521-544.

［21］ GRAVEMEIER V，LENZ S，WALL W A.Towards a taxonomy for multiscale methods in computational mechanics：Building blocks of existing methods［J］.Computational Mechanics，2008，41（2）：279-291.

［22］ ETSION I.State of the art in laser surface texturing［J］.Journal of Tribology，2005，127（1）：248-253.

［23］ MITCHELL N，ELJACH C，LODGE B，et al.Single and reciprocal friction testing of micropatterned surfaces for orthopedic device design［J］.Journal of the Mechanical Behavior of Biomedical Materials，2012，7：106-115.

［24］ SINGH R A，YOON E S.Friction of chemically and topographically modified Si（100）surfaces［J］.Wear，2007，263：912-919.

［25］ MENEZES P L，KISHORE，KAILAS S V，et al.The role of surface texture on friction and transfer layer formation during repeated sliding of Al-4Mg against steel［J］.Wear，2011，271：1 785-1 793.

［26］ GARRIDO A H，GONZÁLEZ R，CADENAS M，et al.Trigological behavior of laser-textured NiCrBSi coatings［J］.Wear，2011，271：925-933.

［27］ PODGORNIK B，VIHENA L M，SEDLA CˇEK M，et al.Effectiveness and design of surface texturing for different lubrication regimes［J］.Meccanica，2012，47（7）：1 613-1 622.

［28］ WANG Hangyu，PREMACHANDRAN N R，ZOU Min，et al.Friction study of a Ni nanodot-patterned surface［J］.Tribology Letters，2007，28（2）：183-189.

［29］ RAMESH A，AKRAM W，MISHRA S P，et al.Friction characteristics of microtextured surfaces under mixed and hydrodynamic lubrication［J］.Tribology International，2013，57：170-176.

［30］ KOVALCHENKO A，AJAYI O，ERDEMIR A，et al.Friction and wear behavior of laser textured surface under lubricated initial point contact［J］.Wear，2011，271：1 719-1 725.

［31］ PETTERSSON U，JACOBSON S.Textured surfaces for improved lubrication at high pressure and low sliding speed of roller／piston in hydraulic motors［J］.Tribology International，2007，40：355-359.

［32］ AYALA P，MAIA da COSTA M E H，PRIOLI R，et al.Nano-and micro-scale wear of fluorinated carbon films［J］.Surface and Coatings Technology，2004，182：335-341.

［33］ GRAC·A S，VILAR R，COLA C·O R.The role of indentation size effect on the abrasive wear behaviour of ductile metallic materials：A nanotribological study［J］.Wear，2010，268：931-938.

［34］ ACHANTA S，DREES D，CELIS J P.Friction and nanowear of hard coatings in reciprocating sliding at milli-newton loads［J］.Wear，2005，259：719-729.

［35］ CHOUQUET C，GAVILLET J，DUCROS C，et al.Effect of DLC surface texturing on friction and wear during lubricated sliding［J］.Materials Chemistry and Physics，2010，123：367-371.

［36］ 张晓亮，钟小华，易戈文，等.Au纳米颗粒织构化表面的黏着和摩擦学行为研究［J］.摩擦学学报，2010，30（6）：607-613.ZHANG Xiaoliang，ZHONG Xiaohua，YI Gewen，et al.Adhesive and frictional properties of Au nanoparticle-textured surfaces［J］.Tribology，2010，30（6）：607-613.

［37］ 吕文斐，方 亮.润滑条件下激光加工纹理的摩擦磨损［J］.摩擦学学报，2009，29（1）：1-4.LYU Wenfei，FANG Liang.Tribological properties of steel surface textured by laser under lubrication［J］.Tribology，2009，29（1）：1-4.

［38］ LI Jianliang，XIONG Dangsheng，DAI Jihui，et al.Effect of surface laser texture on friction properties of nickel-based composite［J］.Tribology International，2010，43：1 193-1 199.

［39］ 朱 华，历建全，陆斌斌，等.变密度微圆坑表面织构在往复运动下的减摩作用［J］.东南大学学报（自然科学版），2010，40（4）：741-745.ZHU Hua，LI Jianquan，LU Binbin，et al.Friction reduction effect of micro-round dimple surface texture with variable density in reciprocating［J］.Journal of Southeast University（Natural Science Edition），2010，40（4）：741-745.

［40］ 刘一静，袁明超，王晓雷.表面织构对发动机活塞／缸套摩擦性能的影响［J］.中国矿业大学学报，2009，38（6）：866-871.LIU Yijing，YUAN Mingchao，WANG Xiaolei.Influence of the surface texture on the tribological performances of piston skirt／liner［J］.Journal of China University of Mining &Technology，2009，38（6）：866-871.

［41］ JIANG Zhaoguo，LU C J，BOGY D B，et al.An investigation of the experimental conditions and characteristics of a nano-wear test［J］.Wear，1995，181：777-783.

［42］ MARUI E，ENDO H.Effect of reciprocating and unidirectional sliding motion on the friction and wear of copper on steel［J］.Wear，2001，249：582-591.

［43］ BONNY K，DE BAETS P，PEREZ Y，et al.Friction and wear characteristics of WC-Co cemented carbides in dry reciprocating sliding contact［J］.Wear，2010，268：1 504-1 517.

［44］ DENG Jianxin，SONG Wenlong，ZHANG Hui，et al.Friction and wear behaviors of the carbide tools embedded with solid lubricants in sliding wear tests and in dry cutting processes［J］.Wear，2011，270：666-674.

［45］ 胡天昌，丁 奇，胡丽天.激光表面织构化对GCr15钢摩擦磨损性能的影响［J］.摩擦学学报，2011，31（5）：447-451.HU Tianchang，DING Qi，HU Litian.The effect of laser texturing of GCr15steel surfaces on their tribological properties［J］.Tribology，2011，31（5）：447-451.

［46］ 解国新，丁建宁，范 真，等.硅基微机械表面粘附及摩擦性能的AFM试验研究［J］.中国机械工程，2006，17（2）：200-203.XIE Guoxin，DING Jianning，FAN Zhen，et al.Adhesive and tribological properties of silicon-surface mems investigated with atomic force microscope（AFM）［J］.China Mechanical Engineering，2006，17（2）：200-203.

［47］ KORRES S，FESER T，DIENWIEBEL M.In situ observation of wear particle formation on lubricated sliding surfaces［J］.Acta Materialia，2012，60（1）：420-429.

［48］ ZHANG L，TANAKA H.Towards a deeper understanding of wear and friction on the atomic scale：A molecular dynamics analysis［J］.Wear，1997，211：44-53.

［49］ YUE L，ZHANG H，LI D Y.Defect generation in nano-twinned，nano-grained and single crystal Cu systems caused by wear：A molecular dynamics study［J］.Scripta Materialia，2010，63（11）：1 116-1 119.

［50］ 林 滨，吴 辉，于思远，等.纳米磨削过程中加工表面形成与材料去除机理的分子动力学仿真［J］.纳米技术与精密工程，2004，2（2）：136-140.LIN Bin，WU Hui，YU Siyuan，et al.Mechanism of material removal and surface generation by molecular dynamics analysis in abrasive processes［J］.Nanoteohnology and Precision Engineering，2004，2（2）：136-140.

［51］ 张俊杰，孙 涛，闫永达，等.单晶铜原子力显微镜加工过程亚表面变形层的分子动力学仿真［J］.机械工程学报，2009，45（1）：174-179.ZHANG Junjie，SUN Tao，YAN Yongda，et al.Molecular dynamics simulation of subsurface deformed layers in nanometric cutting using atomic force microscope pin tool［J］.Journal of Mechanical Engineering，2009，45（1）：174-179.

［52］ 朱朋哲.纳米尺度接触和摩擦的分子动力学及多尺度模拟研究［D］.北京：清华大学，2010.ZHU Pengzhe.Molecular Dynamics and Multiscale Simulation of Contact and Friction on the Nanoscale［D］.Beijing：Tsinghua University，2010.

［53］ INAMURA T，SHIMADA S，TAKEZAWA N，et al.Brittle／Ductile transition phenomena observed in compute simulations of machining defect-free monocrystalline silicon［J］.Annals of the CIRP，1997，46（1）：31-34.

［54］ LIU Yan，ZHANG Xiong，SZE K Y，et al.Smoothed molecular dynamics for large step time integration［J］.Computer Modeling in Engineering Science，2007，20：177-191.

［55］ MAEKAWA K，ITOH A.Friction and tool wear in nano-scale machining：A molecular dynamics approach［J］.Wear，1995，188（1）：115-122.

［56］ YANG J，KOMVOPOULOS K.A molecular dynamics analysis of surface interference and tip shape and size effects on atomic-scale friction［J］.Journal of Tribology，2005，127（3）：513-521.

［57］ GEHLEN P C，HAHN G T，KANNINEN M F.Crack extension by bond rupture in a model of BCC iron［J］.Scripta Metallurgica，1972，6（11）：1 087-1 090.

［58］ GEHLEN P C.Crack extension in a model ofα-iron［J］.Scripta Metallurgica，1973，7（11）：1 115-1 118.

［59］ SINCLAIR J E.The influence of the interatomic force law and of kinks on the propagation of brittle cracks［J］.Philosophical Magazine，1975，31：647-671.

［60］ MULLINS M，DOKAINISH M A.Simulation of the（001）plane crack inα-iron employing a new boundary scheme［J］.Philosophical Magazine A，1982，46（5）：771-787.

［61］ MULLINS M.Atomic simulation of cracks under mixed mode loading［J］.International Journal of Fracture，1984，24（3）：189-196.

［62］ KOHLHOFF S，GUMBSCH P，FISCHMEISTER H F.Crack propagation in b.c.c.crystals studied with a combined finite-element and atomistic model［J］.Philosophical Magazine A，1991，64（4）：851-878.

［63］ RUDD R E，BROUGHTON J Q.Coarse-grained molecular dynamics and the atomic limit of finite elements［J］.Physical Review B，1998，58（10）：5 893-5 896.

［64］ SMIRNOVA J A，ZHIGILEI L V，GARRISON B J.A combined molecular dynamics and finite flement method technique applied to laser induced pressure wave propagation［J］.Computer Physics Communications，1999，118（1）：11-16.

［65］ CAI W，KONING M，BULATOV V，et al.Minimizing boundary reflections in coupled-domain simulations［J］.Physical Review Letters，2000，85（15）：3 213-3 216.

［66］ E Weinan，HUANG Zhongyi.Matching conditions in atomistic-continuum modeling of materials［J］.Physical Review Letters，2001，87（13）：5 501-5 504.

［67］ E Weinan，HUANG Zhongyi.A dynamic atomistic-continuum method for the simulation of crystalline materials［J］.Journal of Computational Physics，2002，182（1）：234-261.

［68］ CLAYTON R W，ENGQUIST B.Absorbing boundary conditions for acoustic and elastic wave equations［J］.Bulletin of the Seismological Society of America，1977，67（6）：1 529-1 540.

［69］ DEYMIER P A，VASSEUR J Q.Concurrent multiscale model of an atomic crystal coupled with elastic continua［J］.Physical Review B，2002，66（13）：4 106-4 110.

［70］ MURALIDHARAN K，DEYMIER P A.SIMMONS J H.A concurrent multiscale finite difference time domain／molecular dynamics method for bridging an elastic continuum to an atomistic system［J］.Modelling and Simulation in Materials Science and Engineering，2003，11（4）：487-501.

［71］ SHENOY V B，SHENOY V，PHILIPS R.Finite temperature quasicontinuum methods［J］.Materials Research Society Symposium Proceedings，1999，538：465-471.

［72］ SHENOY V B.Multi-scale modeling strategies in materials science：The quasicontinuum method［J］.Bulletin of Materials Science，2003，26（1）：742-745.

［73］ LESAR R，NAJAFABADI R，SROLOVITZ D J.Finite-temperature defect properties from free-energy minimization［J］.Physical Review Letters，1989，63（6）：624-627.

［74］ CURTAROLO S，CEDER G.Dynamics of an in homogeneously coarse grained multiscale system［J］.Physical Review Letters，2002，88（25）：5 504-5 507.

［75］ BELYTSCHKO T，XIAO S P.Coupling methods for continuum model with molecular model［J］.International Journal for Multiscale Computational Engineering，2003，1（1）：115-126.

［76］ XIAO S P，BELYTSCHKO T.A bridging domain method for coupling continua with molecular dynamics［J］.Computer Methods in Applied Mechanics and Engineering，2004，193：1 645-1 669.

［77］ WAGNER G J，LIU W K.Coupling of atomistic and continuum simulations using a bridging scale decomposition［J］.Journal of Computational Physics，2003，190（1）：249-274.

［78］ PARK H S，LIU W K.An introduction and tutorial on multiple scale analysis in solids［J］.Computer Methods in Applied Mechanics and Engineering，2004，193：1 733-1 772.

［79］ PARK H S，KARPOV E G，LIU W K.A temperature equation for coupled atomistic／continuum simulations［J］.Computer Methods in Applied Mechanics and Engineering，2004，193：1 713-1 732.

［80］ PARK H S，KARPOV E G，LIU W K，et al.The bridging scale for two-dimensional atomistic／continuum coupling［J］.Philosophical Magazine，2005，85（1）：79-113.

［81］ PARK H S，KARPOV E G，KLEIN P A，et al.Three-dimensional bridging scale analysis of dynamic fracture［J］.Journal of Computational Physics，2005，207（2）：588-609.

［82］ LIU W K，PARK H S.Bridging scale methods for computational nanotechnology［A］.Handbook of Theorectical and Computational Nanotechnology［C］.Valencia：American Scientific Publishers，2006.1-140.

［83］ KADOWAKI H，LIU W K.Bridging multi-scale method for localization problems［J］.Computer Methods in Applied Mechanics and Engineering，2004，193（30）：3 267-3 302.

［84］ TANG S，HOU T Y，LIU W K.A mathematical framework of the bridging scale method［J］.International Journal for Numerical Methods in Engineering，2006，65（10）：1 688-1 713.

［85］ FARRELL D E，KARPOV E G，LIU W K.Algorithms for bridging scale method parameters［J］.Computational Mechanics，2007，40（6）：965-978.

［86］ SHILKROT L E，MILLER R E，CURTIN W A.A coupled atomistic／continuum model of defects in solids［J］.Journal of the Mechanics and Physics of Solids，2002，50（10）：2 085-2 106.

［87］ SHILKROT L E，MILLER R E，CURTIN W A.Coupled atomistic and discrete dislocation plasticity［J］.Physical Review Letters，2002，89（2）：502-510.

［88］ SHILKROT L E，MILLER R E，CURTIN W A.Multiscale plasticity modeling：Coupled atomistics and discrete dislocation mechanics［J］.Journal of the Mechanics and Physics of Solids，2004，52（4）：755-787.

［89］ MILLER R E，SHILKROT L E，CURTIN W A.A coupled atomistics and discrete dislocation plasticity simulation of nanoindentation into single crystal thin films［J］.Acta Materialia，2004，52：271-284.

［90］ QU S，SHASTRY V，CURTIN W A，et al.A finite-temperature dynamic coupled atomistic／discrete dislocation method［J］.Modelling and Simulation in Materials Science and Engineering，2005，13（7）：1 101-1 118.

［91］ HOLIAN B，RAVELO R.Fracture simulations using large-scale molecular dynamics［J］.Physical Review B，1995，51（11）：275-288.

［92］ SHIARI B，MILLER R E，CURTIN W A.Coupled atomistic／discrete dislocation simulations of nanoindentation at finite temperature［J］.Journal of Engineering Materials and Technology，2005，127（4）：358-368.

［93］ LUAN B Q，HYUN S，MOLINARI J F，et al.Multiscale modeling of two-dimensional contacts［J］.Physical Review E，2006，74（4）：6 710-6 720.

［94］ PARK H S，KARPOV E G，LIU W K.Non-reflecting boundary conditions for atomistic，continuum and coupled atomistic／continuum simulations［J］.International Journal for Numerical Methods in Engineering，2005，64（2）：237-259.

［95］ LIU W K，KARPOV E G，ZHANG S，et al.An introduction to computational nanomechanics and materials［J］.Computer Methods in Applied Mechanics and Engineering，2004，193：1 529-1 578.

［96］ KARPOV E G，WAGNER G J，LIU W K.A Green’s function approach to deriving wave-transmitting boundary conditions in molecular dynamics simulations［J］.International Journal for Numerical Methods in Engineering，2005，62：1 250-1 262.

［97］ KARPOV E G，YU H，PARK H S，et al.Multiscale boundary conditions in crystalline solids：Theory and application to nanoindentation［J］.International Journal of Solids and Structures，2006，43（21）：6 359-6 379.

［98］ CUI J Z，GANG Y X.The multi-scale methods for stiffness and strength parameter computation of composites［A］.7th World Congress on Computational Mechanics（WCCM Ⅶ）［C］.Los Angeles：［s.n.］，2006.2 340-2 349.

［99］ 杨 卫.微纳米尺度的力学行为［J］.世界科技研究与发展，2004，26（4）：2-6.YANG Wei.The mechanics characteristic of micro-nanoscale［J］.World Sci-tech R &D，2004，26（4）：2-6.

［100］ 白以龙，汪海英，夏蒙棼，等.固体的统计细观力学——连接多个耦合的时空尺度［J］.力学进展，2006，36（2）：286-305.BAI Yilong，WANG Haiying，XIA Mengfen，et al.Statistical mesomechanics of solid，linking coupled multiple space and time scales［J］.Advances in Mechanics，2006，36（2）：286-305.

［101］ 张洪武，张 盛，毕金英.周期性结构热动力时间-空间多尺度分析［J］.力学学报，2006，38（2）：226-235.ZHANG Hongwu，ZHANG Sheng，BI Jinying.Thermodynamic analysis of multiphase periodic structures based on a spatial and temporal multiple scale method［J］.Chinese Journal of Theoretical and Applied Mechanics，2006，38（2）：226-235.

［102］ AGRAWAL P M，RICE B M，THOMPSON D L.Predicting trends in rate parameters for self-diffusion on FCC metal surfaces［J］.Surface Science，2002，515（1）：21-35.

［103］ SWOPE W C，ANDERSEN H C，BERENS P H，et al.A computer simulation method for the calculation of equilibrium constants for the formation of physical clusters of molecules：Application to small water clusters［J］.The Journal of Chemical Physics，1982，76（1）：637-649.