域上上三角矩阵空间的保持幂等的函数
樊玉环,王佩臣
(黑龙江工程学院数学系,黑龙江哈尔滨 150001)
研究各种不变量以及不变量保持的映射和变换历来是数学学科领域关注的问题。在矩阵理论研究中,保持问题已成为一个十分活跃的研究领域,一方面是因为它的理论价值;另一方面是因为这些问题在微分方程、系统控制、数理统计等领域有着实际应用背景。关于保持问题的研究,许多学者做了大量的工作,取得了丰厚的成果[1-14]。YAO等研究了全矩阵空间上的保持幂等的函数的形式[1],文献[2]研究了保持幂等的矩阵加群自同态,随后,大量的文献研究了特殊矩阵空间上的保持幂等的算子[3-4],但关于特殊矩阵空间上的保持幂等的函数文献至今还没有,本文刻画了上三角矩阵空间上保持幂等的函数的形式,并作为应用,刻画了上三角矩阵空间上保持立方幂等的函数的形式,上三角矩阵空间上保持k-幂等的函数的形式及上三角矩阵空间上保{1,2}逆的函数的形式。
1 符号及基本概念
用N表示自然数集,设F是任意给定的域,F*表示F/{0},Mn(F)为F上所有n阶矩阵的全体,Tn(F)为F上所有n阶上三角矩阵的全体。
定义1[1]称函数f:F→F是域上上三角矩阵空间的保持幂等的函数,如果f满足:
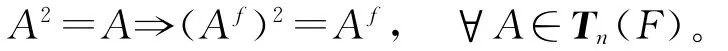
称函数f:F→F是域上上三角矩阵空间的保持立方幂等的函数,如果f满足:

称函数f:F→F是域上上三角矩阵空间的保持{1,2}逆的函数,如果f满足:

定义2[15]设k∈N且k≥2,A∈Mn(F),若Ak=A,则称A是k-幂等。特别地,当k=2时,称A是幂等的;当k=3时,称A是立方幂等的。
定义3[15]设A∈Mn(F),如果X∈Mn(F)是矩阵方程AXA=A和XAX=X的解,则称X是A的{1,2}逆。
定义4[16]称f:F→F是同态,如果f满足f(a+b)=f(a)+f(b),f(ab)=f(a)f(b)。
2 基本结论
定理1 函数f是域上上三角矩阵空间的保持幂等的充要条件是下列结论之一成立:
1)f≡0;2)f≡;3)f是域F上的单的自同态。
证明 充分性显然,下面证明必要性。
步骤1 证明f(0)=0或f(0)=

通过直接计算得到
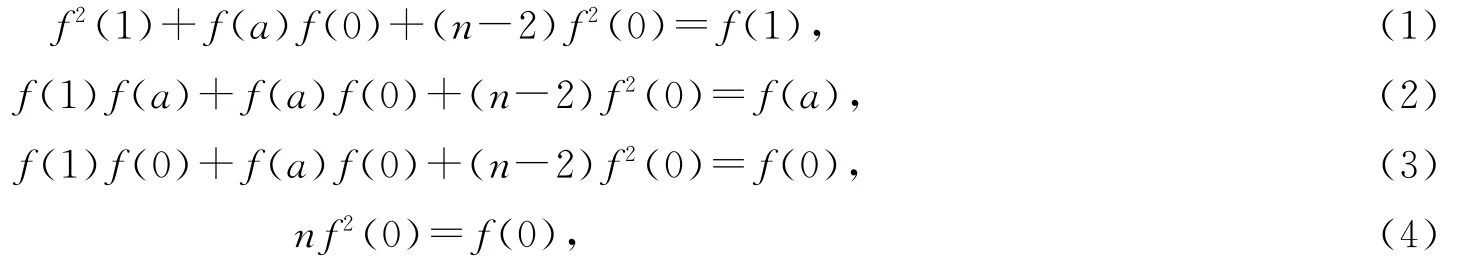
由式(4)得f(0)=0或f(0)=
步骤2 证明当f(0)=时
在式(3)中令a=1得到

步骤3 证明当f(0)=0时,2种情况f≡0及f是域F上的单的自同态。
将f(0)=0代入式(1)得f2(1)=f(1)。故f(1)=0或1。
下面分2种情况。
第1种情况:f(0)=0,f(1)=0。
将f(0)=0,f(1)=0代入式(2)得f(a)=0,∀a∈F*,从而f≡0,这就完成了结论1)的证明。
第2种情况:f(0)=0,f(1)=1。

通过计算得到


通过计算得到

应用式(6)及式(7)得到
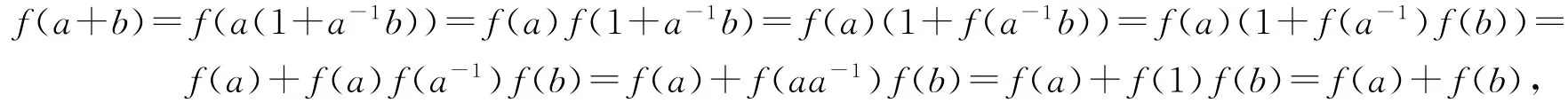
即

由式(6)及式(8)可得f是域F上的自同态。由式(6)得到
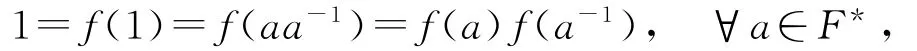
故

由f的定义可知:
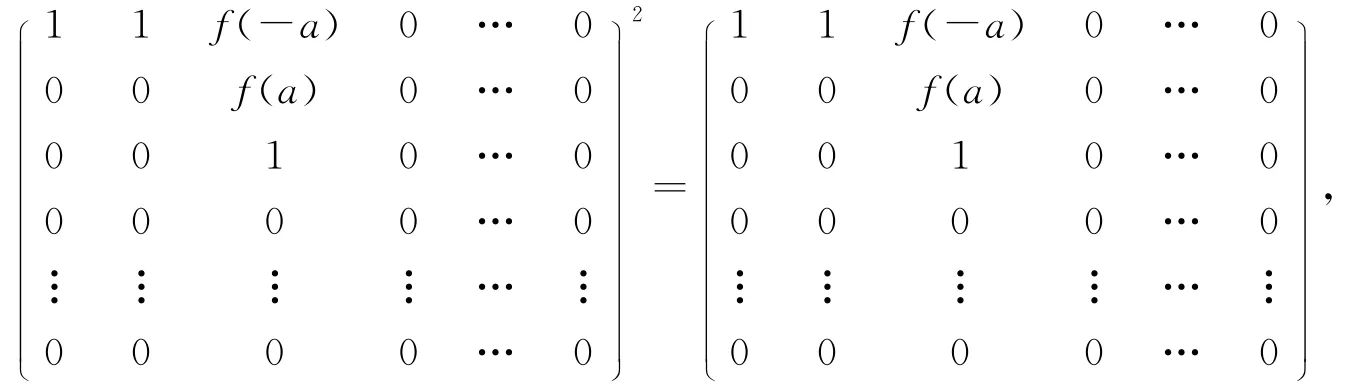
通过计算得到

若f(a)=f(b),则应用式(8)、式(9)及式(10)可得a=b。
从而f是域F上的单的自同态。这就完成了结论3)的证明。
作为本定理的应用可得域上上三角矩阵空间的几个定理。
定理2 函数f是域上上三角矩阵空间的保持立方幂等的充要条件是下列结论之一成立:
1)f≡0;2)f≡;4)f=cδ,δ是域F上的单自同态。
在定理2证明中上三角立方幂等矩阵的选取如定理1,式(4)则变成nf3(0)=f(0),从而f(0)=0,-。结论4)中令c=f(1)。
定理3 函数f是域上上三角矩阵空间的保持k-幂等的充要条件是下列结论之一成立:
1)f≡0;2)f≡,ε为k-1次单位根;3)f=cδ,δ是域F上的单自同态。
定理4 函数f是域上上三角矩阵空间的保持{1,2}逆的充要条件是下列结论之一成立:
1)f≡0;2;4)f=cδ,δ是域F上的单自同态。
/References:
[1] YAO Hongmei,SONG Xiaocui,WANG Guanghui.A note on functions preserving some properties of matrices[A].Proceeding of the Sixth International Conference of Matrices and Operators[C].[S.l.]:[s.n.],2011.77-80.
[2] CAO Chongguang,ZHANG Xian.Additive operators preserving idempotent matrices over field and applications[J].Lin Alg Appl,1996,248:327-338.
[3] 张 显,曹重光.域上上三角矩阵空间保幂等与立方幂等的加法单映射[J].数学杂志,2004,24(4):416-420.ZHANG Xian,CAO Chongguang.Additive injective maps preserving idempotence and tripotence on the space of triangular matrices over fields[J].J of Math,2004,24(4):416-420.
[4] 佟 鑫,曹重光.域上从对称矩阵空间到全矩阵空间保幂等的线性算子[J].黑龙江大学自然科学学报,2003,20(3):25-28.TONG Xin,CAO Chongguang.Linear operators preserving idempotence from symmetric matrix spaces to all matrix spaces over a field[J].Journal of Natural Science of Heilongjiang University,2003,20(3):25-28.
[5] 张 显,曹重光.保不变量的矩阵加群同态[M].哈尔滨:哈尔滨出版社,2001.ZHANG Xian,CAO Chongguang.Additive Operators Preserving Invariants[M].Harbin:Harbin Press,2001.
[6] 华罗庚,万哲先.典型群[M].上海:上海科技出版社,1962.HUA Luogeng,WAN Zhexian.Classical Groups[M].Shanghai:Shanghai Science and Technology Press,1962.
[7] CHAN G,LIM M,TAN K.Linear preservers on matrices[J].Linear Algebra Appl,1987,93:67-72.
[8] LI C,PIERCE S.Linear preservers problems[J].Am Math Mon,2001,108(7):591-605.
[9] 曹重光.实数域上有限可除代数矩阵空间保幂等的线性算子[J].数学杂志,1992,12(3):349-353.CAO Chongguang.Linear operators preserving idempotent on the finite division algebra matrix space over the real number field[J].J of Math,1992,12(3):349-353.
[10] 曹重光.某些环上矩阵模的保幂等的线性映射[J].黑龙江大学自然科学学报,1999,16(1):1-4.CAO Chongguang.Linear maps preserving idempotent of matrix module over the some rings[J].Journal of Natural Science of Heilongjiang University,1999,16(1):1-4.
[11] MARCUS M.All Linear operators leaving the unitary group invariant[J].Duke Math J,1959,26(1):155-163.
[12] MARCUS M,WESTWICK R.Linear maps on skew symmetric matrices:The invariance of elementary symmetric functions[J].Pacific J Math Mon,1960,10:917-924.
[13] 侯晋川,崔建莲.算子代数上线性映射引论[M].北京:科学出版社,2002.HOU Jinchuan,CUI Jianlian.Introduction to Linear Maps on the Operator Algebras[M].Beijing:Science Press,2002.
[14] 杨静梅,冯 爽,姚 卫.Heyting代数中同余关系的简化[J].河北科技大学学报,2012,33(6):479-481.YANG Jingmei,FENG Shuang,YAO Wei.Simplification of congruence yelation in Heyting algebra[J].Journal of Hebei University of Science and Technology,2012,33(6):479-481.
[15] CAO Chongguang.Linear operators that preserve M-P inverses of matrices[J].Northeast Math J,1993,9(2):255-260.
[16] 张 显.交换整环上的上三角矩阵的保幂等的线性算子[J].新疆大学学报,1993,10(2):25-27.ZHANG Xian.Linear operators preserving idempotent on the upper triangular matrix over commutative domain[J].Journal of Xinjiang University,1993,10(2):25-27.

