Al/Zr多层膜生长模型和数值计算*
杨传春,钟 奇,张 众
(同济大学 物理系 先进微结构材料教育部重点实验室,上海 200092)
引 言
近年来,为了对太阳光谱进行深入的研究,具有高效反射性能的硅基多层膜元件已经在一些近正入射反射系统的装置中得到应用。但是随着衍射极限的减小,光学表面和多层膜膜层界面的微粗糙限制了光学元件的性能,光与元件相互作用时产生的非镜向散射,不仅减小了系统的光通量,而且也降低了像的对比度。随着入射光波长的减小,背向散射强度将以1/λ2的形式增长[1]。
散射理论从70年代开始发展至今,人们对散射的理解有了一些进展。早期许多工作者主要针对X射线掠入射式多层膜,研究其界面粗糙度对散射光的影响。而作为EUV 光波段光散射研究的先驱,Spiller[2]和Stearns[3]等人研究了正入射时多层膜界面粗糙度对光散射的影响。1992年,Stearns[4]等人基于多层膜的无定形生长过程提出了界面粗糙度动态生长理论。2011年,Marcus Trost[5]等人在EUV 光波段对正入射式Mo/Si多层膜反射镜的背向散射作了实验测定,并应用动态生长理论对钼硅多层膜的散射作了比较分析,结果发现理论与测试数据吻合较好。
在17~19nm 的极紫外波段,Al/Zr多层膜是具有最高理论反射率的Al基多层膜,因而具有光明的应用前景,并得到了广泛研究[6-7]。在以前的研究中[8],发现Al/Zr多层膜的膜层界面粗糙度造成了多层膜反射率的减小,而且界面粗糙度随多层膜的生长而逐渐增大。但是,对于Al/Zr多层膜的膜层界面粗糙度的动态变化规律尚没有开展深入的研究。
本文以Stearns的多层膜界面粗糙度动态生长理论为基础,对EUV 光波段近正入射Al/Zr多层膜生长模型作了分析和计算,并通过与实验测量结果的对比,对Stearns粗糙度动态生长理论的适用条件作了补充性讨论,给出了Al/Zr多层膜界面粗糙度基于Stearns动态变化规律的使用范围。
1 多层膜动态生长理论
薄膜的生长过程可用薄膜粗糙表面任意两点间的高度差的h(r)的连续性方程来描述:

其中,r为薄膜表面任意两点间的水平距离,τ为薄膜的厚度,v为描述弛豫过程的独立参数,η表示随机噪声。当v为正值时,右边第一项将使表面粗糙度变小,而第二项将使表面粗糙度增加。弛豫过程的指数p因薄膜生长的机理不同而异,一般情况下,粘性流体:p=1,蒸发和凝结:p=2,体扩散:p=3,表面扩散:p=4[9]。Tong和Willians[10]认为,v取负值,可以适用于描述三维岛状生长的薄膜表面。
式(1)表明,薄膜的生长是生长过程与弛豫过程间竞争的结果,生长过程较快时,膜层表面容易表现出粗糙和各向异性;弛豫过程较快时,膜层表面容易表现出平滑和各向同性的特点。
应当指出的是,式(1)是表面生长模型中最简单的一种可能。它是对粗糙表面形成过程线性的和局部的处理。Kardar等人[11]首先用一非线性项(ΔH)2对式(1)作了修正,该项表示在各向同性的特定沉积条件下,薄膜将沿着法线方向生长。当沉积角度或表面倾斜较大时,表面粗糙度的形成是局部的这个假设就不再成立了,在这种情况下,表面某点的沉积依赖于表面的遮蔽效应。Karunasiri等人[12]和Tang等人[13]也提出了一个生长模型,实现了局部生长(遮蔽)机理的理论模拟。当生长过程是由非线性和局部性引起时,薄膜将以尖瓣和柱状这种不连续的形状快速生长。这些特征可以在薄膜的形貌中观察到,尤其是低能沉积过程中的薄膜。相比较,本文只考虑粗糙度较小的光学多层膜,这种薄膜可以通过高能生长过程来实现,如低气压下的溅射镀膜过程。保证了表面粗糙度不至于大到影响薄膜的线性或非局部生长模式,这种观点得到了多层膜实验研究的支持[14]。
与单层膜生长不同的是,多层膜动态生长理论认为,薄膜各个界面的粗糙度一方面复制于相邻的先期生长的膜层表面粗糙度,另一方面也有不完美生长过程引起的内部固有粗糙度。第i个界面可以用其粗糙度hi(r)的频谱函数来表示[4]:

其中γi表示正在生长的膜层内部的固有粗糙度,角标i-1 代表相邻的先期生长的膜层,为界面粗糙度复制因子,它是空间频率f 的函数,反映第i个膜层对第i-1个膜层表面的“记忆程度”。复制函数取值介于0~1之间的实数时,表明第i层膜的粗糙度既受第i-1层膜的表面粗糙度影响,又受自身内部固有粗糙度的影响。
对于无定形生长的N 层多层膜,由于表面粗糙度的功率谱密度(PSD(f)=〈h(f)h*(f)〉)通常便于测量,因此用功率谱密度作为多层膜表面粗糙度的统计表述,更便于与测量结果的对比。若多层膜界面粗糙度结构可以看作是自由分布,粗糙度的功率谱密度反应的是整个界面粗糙度的均值,则功率谱密度的值可以由粗糙度频率谱函数的傅里叶变换来表示,在理论上与粗糙表面结构的描述等价。通过对式(2)进行迭代运算可得多层膜表面粗糙度的功率谱密度函数与界面粗糙度之间的关系为[15]:
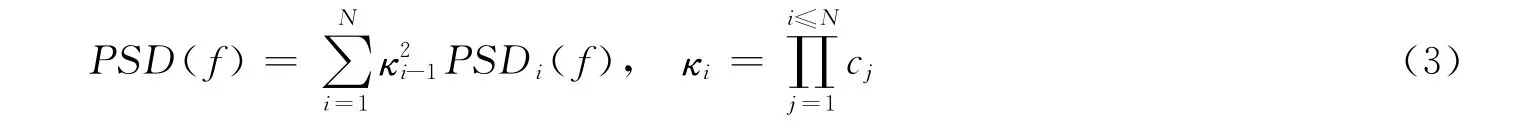
其中,PSDi为膜层生长过程中因内部缺陷等原因引起的固有粗糙度对应的功率谱密度,在膜层生长过程中没有明显晶向分布时,PSDi由下式确定[4]:

其中,di为第i层膜的厚度,Ωi是多层膜结构中第i层薄膜的膜层材料的原子团簇体积。
式(3)是多层膜动态生长理论的公式表述形式,反映了多层膜的复杂生长过程。可以看到,多层膜的表面功率谱密度与膜层的厚度和数目、原子团簇体积、弛豫过程、生长机理等诸多因素相关。通过式(3)的迭代计算,可以将多层膜表面粗糙度和所用基板的表面粗糙度联系起来,从而为表面多层膜界面结构变化情况测量提供了理论依据。计算过程中,只需要先对基板表面粗糙度的测量结果进行傅里叶变换,然后基于功率谱密度函数进行迭代运算,运算过程中避免了相关函数的运算,最后对于多层膜表面的粗糙度功率谱密度再进行一次傅里叶变换,就可以得到多层膜表面粗糙度的理论预期值。
2 实 验
在实验中,采用掺氟的二氧化硅作为Al/Zr多层膜样品的基板,采用国产超高真空磁控溅射设备(J GP560C6)实现Al/Zr多层膜样品的制备。制备多层膜的靶材料为美国Kurt J.Lesker公司生产,Al靶材为掺杂了Si(1%wtSi)的合金材料,Zr靶材的纯度为99.95%。在溅射镀膜设备的真空腔内,溅射阴极靶与基板垂直相对,靶在下,基板在上,两者间距离为10cm。在沉积Al/Zr多层膜之前,真空系统的本底真空度低于8×10-5Pa。溅射工作气体为高纯度的氩气(纯度:99.999%)。在镀膜过程中,溅射工作气压为0.18Pa。Al和Zr靶均采用恒功率模式的直流磁控溅射方法,其中,Al靶材的功率为40W,Zr靶材的功率为30W。在多层膜制备过程中,基板一直保持自转,转速为20r/min。通过步进电机控制基板公转,使其交替停留在Al和Zr靶上方,由基板在靶材上方停留的时间来控制相应膜层的厚度。本文所制备的样品共四个,每个样品的周期厚度设计值为9.0nm,其中Zr膜层的厚度与周期厚度之比为0.33。四个样品的周期数(N)分别为10,40,60,80。
利用原子力显微镜(atomic force microscope,AFM)(生产厂商:Veeco,型号:DI 3100)实现多层膜样品的表面粗糙度度测量,并给出了相应的表面粗糙度的功率谱密度。在合肥国家同步辐射实验室的辐射计量与标准束线的反射率计上实现了Al/Zr多层膜在极紫外波段的反射率测量。
3 实验结果分析和数值计算
图1给出了不同膜对数的Al/Zr多层膜表面原子力显微镜测量结果,其中图1(a)~图1(d)分别对应N=10、40、60 和80 的Al/Zr多层膜,它们的表面粗糙度的均方根(root-mean-square,RMS)值分别为0.403nm(N=10)、0.401nm(N=40)、0.544nm(N=60)和0.817nm(N=80)。测量结果表明,对于Al/Zr多层膜,当膜对数不超过40时,其表面粗糙度基本不随膜对数的增加而变化;当膜对数超过40时,其表面粗糙度随膜对数的增加而逐渐增大。

图1 包含不同膜对数的Al/Zr多层膜表面原子力测量结果Fig.1 AFM measurement result of Al/Zr multilayers with variable layer pairs
图2给出了相应多层膜样品表面粗糙度的二维功率谱密度。由图可知,随着空间频率的增大(从中心向四周),多层膜表面粗糙度的功率谱密度不断减小(从亮到暗),表明多层膜的表面粗糙度并无明显的周期性变化。随着膜对数的增加,表面粗糙度的二维表面功率谱密度形状发生了变化,N=10和N=40时,功率谱密度图形呈圆形,表明当膜对数较少时,Al/Zr多层膜的表面粗糙度的分布与方向无关,满足随机分布的特点;N=60和N=80时,功率谱密度图形呈现椭圆形,表明膜对数较多时,Al/Zr多层膜的表面粗糙度沿x 方向和y 方向的分布有差异,分布具有一定的“方向性”。
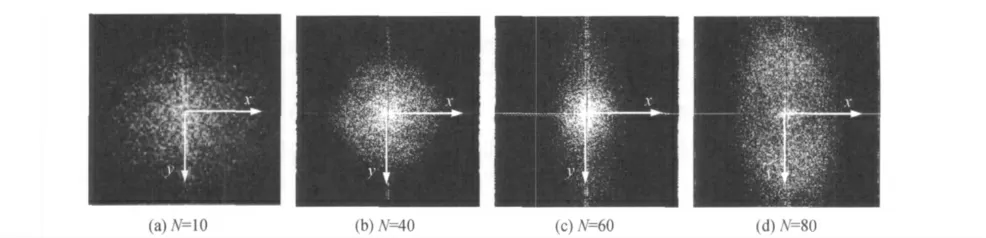
图2 包含不同膜对数的Al/Zr多层膜表面粗糙度的二维功率谱密度Fig.2 2Dpower spectrum density of surface roughness for Al/Zr multilayers with variable layer pairs
图3 给出了包含不同膜对数的Al/Zr多层膜在极紫外波段的反射率设计、测量和理论拟合曲线。由图可以看到,由于膜层界面间的粗糙度较大,导致了Al/Zr多层膜的测量反射率均低于设计值。另外,随着膜对数的增加,Al/Zr多层膜的测量反射率先增大后减小,这是由于膜层界面间粗糙度随着膜对数的增加而动态增长造成的[8]。为了能够从理论上分析膜层界面粗糙度对多层膜反射率的影响,现对多层膜的测量反射率进行理论模拟。具体处理过程如下:

图3 Al/Zr多层膜反射率的设计、测量和理论拟合曲线图Fig.3 The design,measured and theoretical fitting reflectivity of Al/Zr multilayers
首先利用AFM 对二氧化硅基底的表面粗糙度进行采样,并计算粗糙度的功率谱密度。然后根据多层膜动态生长理论,计算Al/Zr多层膜每个界面的粗糙度功率谱密度,直到最终计算出多层膜表面粗糙度的功率谱密度。最后将表面功率谱密度利用式(5)转换成均方根粗糙度[16]。
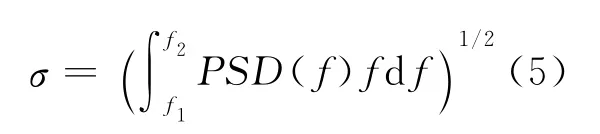
多层膜中Al膜层和Zr膜层的厚度及表面ZrO2层的厚度主要根据测量反射率的峰值位置来确定,本文所用的各膜层厚度如表1所示,拟合所用的膜层材料折射率来自于软件IMD[17]提供的数据。
式(5)中的空间频率积分范围完全由所采用仪器的测量范围和精度确定,其中功率谱密度既可使用一维功率谱密度,也可使用二维功率谱密度,所不同的是粗糙度的空间频率上限取值不同。本文采用二维功率谱密度进行计算,x和y方向上空间功率谱密度的上限取f2=2.56×10-2nm-1,下限取f1=2.0×10-4nm-1,Al和Zr的弛豫因子取值分别为0.008nm3和0.4nm3,薄膜生长采用表面扩散模型(p=4),Al和Zr的原子团簇体积分别为0.017nm3和0.023nm3。

表1 Al/Zr多层膜膜层厚度理论值Tab.1 Theoretical thickness of Al/Zr multilayers with variable layer pairs
图4给出了基于多层膜动态生长理论计算的、不同膜对数的Al/Zr多层膜表面粗糙度的RMS 值(实线)以及N=10、40、60和80的Al/Zr多层膜表面粗糙度RMS 值。由图4可以看出,理论计算的多层膜界面粗糙度随膜层材料的交替呈现振荡的变化趋势。N≤40,理论计算值随膜层数振荡下降,与实验值吻合较好;N>40,理论计算值保持水平振荡,而实验测得的均方根粗糙度显著地增大,理论与实验结果的差异越来越大。
造成这种差异的主要原因可能是:Stearns提出的多层膜动态生长理论,有着明确的约束条件:膜层生长过程中没有明显的晶向,即膜层生长是无定形相的,表面粗糙度满足随机分布的特征[4],Al和Zr的弛豫因子随膜对数的增加而保持不变;而根据图2 中,多层膜表面粗糙度功率谱密度的变化,可以证明,当N>40时,Al和Zr的弛豫因子全部或者至少一个发生了变化,这种变化很可能是由于Al膜层明显的结晶造成的[8]。因此,当N>40,多层膜的表界面粗糙度的大小已经不能用多层膜动态生长理论来描述了。
综上所述,虽然N≤40,Al膜的生长条件与理论模型有差异,但是动态生长理论仍然很好地反映了膜层粗糙度的变化情况;但是,当N>40,膜层材料的弛豫因子产生了变化,表面粗糙度不再是随机分布,因此也就不能再用多层膜动态生长理论来描述了。
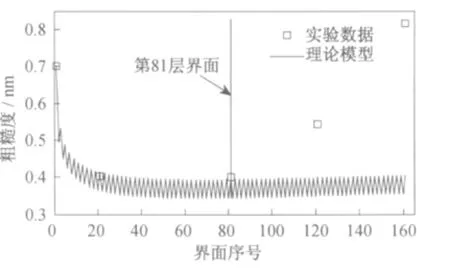
图4 Al/Zr多层膜表面粗糙度理论计算与测量值Fig.4 The theoretical and measured surface roughness of Al/Zr multilayers with variable layer pairs
4 结 论
基于Al/Zr多层膜的生长过程,利用原子力显微镜对包含不同膜对数的多层膜的表面粗糙度进行了测量,结合动态生长理论模型对铝锆多层膜的表界面粗糙度进行了计算,并用于对多层膜反射率的理论拟合。计算结果表明,膜对数N≤40的条件下,Al/Zr多层膜的表面均方根粗糙度变化符合多层膜动态生长理论模型,反射率随膜层数增加而增大,并逐渐趋于饱和;当N>40时,多层膜表面均方根粗糙度明显大于理论计算值,峰值反射率也随着膜对数的增加而逐渐减小。对于Al/Zr多层膜,N≤40是多层膜表界面粗糙度动态生长理论的应用条件。
[1] GULLIKSON E M.Scattering from normal incidence EUV optics[J].SPIE,1998,3331:72-80.
[2] SPILLER E.Low-loss reflection coatings using absorbing materials[J].Appl Phys Lett,1972,20(9):365-369.
[3] STEARNS D G,GULLIKSON E M,Nonspecular scattering from extreme ultraviolet multilayer coatings[J].Physica B,2000,283:84-91.
[4] STEARNS D G,GAINES D P,SWEENEY D W.Nonspecular x-ray scattering in a multilayer coated imaging system[J].J Appl Phys,1998,84(2):1003-1028.
[5] SCHRÖDER S,HERFFURTH T,TROST M,et al.Angle-resolved scattering and reflectance of extreme-ultraviolet multilayer coatings:measurement and analysis[J].Appl Opt,2010,49(9):1503-1512.
[6] HU M H,GUEN K L,ANDRÉ J M,et al.Structural properties of Al/Mo/SiC multilayers with high reflectivity for extreme ultraviolet light[J].Opt Express,2010,18(19):20019-20028.
[7] VORONOV D L,ANDERSON E H,CAMBIE R,et al.A 10,000groove/mm multilayer coated grating for EUV spectroscopy[J].Opt Express,2011,19(7):6320-6325.
[8] ZHONG Q,LI W B,ZHANG Z,et al.Optical and structural performance of the Al(1%wtSi)/Zr reflection multilayers in the 17-19 nm region[J].Opt Express,2012,20(10):10692-10700.
[9] HERRING C.Diffusional viscosity of a polycrystalline solid[J].J Appl Phys,1950,21(5):437-445.
[10] TONG W M,WILLIAMS R S.Kinetics of surface growth:phenomenology,scaling,and mechanisms of smoothening and roughening[J].Annu Rev Phys Chem,1994,45:401-438.
[11] KARDAR M,PARISI G,ZHANG Y C.Dynamic scaling of growing interfaces[J].Phys Rev Lett,1986,56(9):889-892.
[12] KARUNASIRI R P U,BRUINSMA R,RUDNICK J.Thin-film growth and the shadow instability[J].Phys Rev Lett,1989,62(7):788-791.
[13] TANG C,ALEXANDER S,BRUINSMA R,et al.Scaling theory for the growth of amorphous films[J].Phys Rev Lett,1990,64(7):772-775.
[14] SCHRÖDER S,DUPARRÉ A,CORIAND L,et al.Modeling of light scattering in different regimes of surface roughness[J].Opt Express,2011,19(10):9820-9835.
[15] TROST M,SCHRÖDER S,FEIGL T,et al.Influence of the substrate finish and thin film roughness on the optical performance of Mo/Si multilayer[J].Appl Opt,2011,50(9):C148-C153.
[16] HARVEY J E,SCHRÖDER S,CHOI N,et al.Total integrated scatter from surfaces with arbitrary roughness,correlation widths,and incident angles[J].Opt Eng,2012,51(1):.013402-1-013402-10.
[17] WINDT D L.IMD-software for modeling the optical properties of multilayer films[J].Comp in Phys,1998,12(4):360-370.

