斯密特棱镜偏振特性的Mueller矩阵法分析和检测＊

卢进军，朱维兵

（西安工业大学 光电工程学院，陕西 西安 710032）

引 言

斯密特棱镜作为光学系统中广泛使用的含屋脊的棱镜之一，其偏振特性对成像质量的影响——偏振像差近年来广受关注［1］。已经研究得知，斯密特棱镜偏振特性直接导致了艾里斑的中心分裂，是破坏成像质量的主要成因［2］。随之而来的偏振像差的矫正工作已经出现，矫正效果的评价提出了对偏振特性测量方法的需求。按照偏振光学理论，光学零件和光学系统的偏振特性可以由Jones矩阵、Mueller矩阵和Pauli矩阵三种矩阵来分析和描述，Jones矩阵是一个二阶复数矩阵，是矩阵方法中最简单的，但只能用于完全偏振光［3－4］。Mueller矩阵是一个四阶实数矩阵，可以用于处理所有状态的光波而被广泛研究和使用［5－7］。Pauli矩阵作为Jones矩阵数学展开式，为Jones矩阵法提供了重要的研究基础［8］。这三种矩阵用于光学器件的偏振特性分析具有各自的优势。对光学器件或系统的偏振特性的检测大多是通过对其特征矩阵的检测来进行［9］。Mueller矩阵是用斯托克斯参量法研究光波的偏振特性时的光学器件或系统的特征矩阵。Mueller矩阵具备全面表征光学器件偏振特性的形式，双向衰减、位相延迟等信息就直接包含在Mueller矩阵中，测量光学元件的Mueller矩阵就可以全面了解光学器件的偏振特性，对于偏振分析起着重要作用。

图1 斯密特棱镜Mueller矩阵测量原理图Fig.1 Principle of Schmidt prism Mueller matrix measurement

1 Mueller矩阵检测原理分析

斯托克斯参量法分析偏振态，需要测试的步骤多，过程繁杂容易出错，而且测量结果与入射光的偏振态有关，并不是被测器件的独立偏振特性。Mueller矩阵的最大特点是测量结果只与被测光学元件有关，从Mueller矩阵相应的矩阵元与透射振幅和位相的关系中即可以确定斯密特棱镜的偏振特性。

用傅里叶级数法测试斯密特棱镜Mueller 矩阵［10］，其测量原理如图1所示。

测量装置由He－Ne激光器、起偏组合、斯密特棱镜、检偏组合、探测器五部分构成，起偏组合是起偏器P1和四分之一波片W1，检偏组合是检偏器P2和四分之一波片W2。测试前，起偏器和检偏器的偏振方向均保持在水平方向，四分之一波片W1和四分之一波片W2一起旋转，两个四分之一波片旋转角度以1∶5的比例进行增加，如果四分之一波片W1的快轴与水平方向的夹角为θ，那么，四分之一波片W2的快轴与水平方向夹角为5θ。

已知线偏器的振动方位角为0°时的Mueller矩阵为：

其中p1为起偏器P1的Mueller矩阵，p2为检偏器P2的Mueller矩阵。

起偏组合四分之一波片W1的快轴与水平方向的夹角为θ，则该四分之一波片的Mueller矩阵为：

检偏组合中的四分之一波片的旋转角度是起偏组合中四分之一波片旋转角度的5倍，因此该波片的Mueller矩阵可以写成：

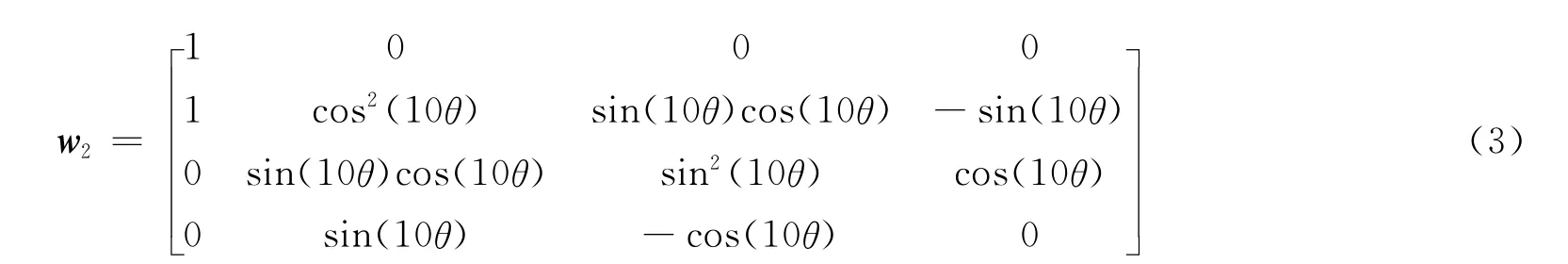
斯密特棱镜的Mueller矩阵为：

那么，经过起偏组合、斯密特棱镜、检偏组合后出射光波的斯托克斯矢量可以表示成：

其中Sin为入射光的斯托克斯矢量。

在斯托克斯矢量中，第一行代表的是总光强，而实验中测得的也是光强值，所以只要考虑出射光的斯托克斯矢量的第一行，上式出射光的斯托克斯矢量是4×1的列向量，由于只考虑第一行，因此可以写成：

其中

该光强又可以用傅里叶级数的形式表示为［10］：

对比式（7），式（8）可以知道傅里叶级数的系数是关于Mueller矩阵矩阵元的函数，那么，傅里叶级数的系数可以用Mueller矩阵的矩阵元来表示，故只要计算出傅里叶级数的系数，就可以获得Mueller矩阵元。以下是Mueller矩阵元与傅里叶级数的系数的关系：

2 斯密特棱镜Mueller矩阵的检测

2.1 测试实验

一束入射光经过斯密特棱镜时，将同时经由两条路径传播，实验分别针对这两条传播路径检测出射光的强度。图2是测量斯密特棱镜Mueller矩阵的实验系统图。

起偏器和检偏器保持不变，两个四分之一波片快轴按照1∶5的比例进行旋转，用功率计记录相应的光强值由表1列出。

图2 斯密特棱镜Mueller矩阵检测实验系统Fig.2 Experimental system of Schmidt prism Mueller matrix measurement

表1 测量两路径的光强值Tab.1 Measurement of the intensity values of the two paths mW

出射光的光强可以用式（8）来表示，因此把实验得到的光强值代入到该式中，借助MATLAB对25个线性方程组进行方程的计算，得到傅里叶级数的系数如下：

这些傅里叶系数与矩阵元的关系如前所述，那么计算得到斯密特棱镜的Mueller矩阵：

2.2 测量结果分析

在Mueller矩阵中，已经有相关矩阵元描述s光的振幅衰减，p光的振幅衰减，s光的位相延迟，p光的位相延迟。Mueller矩阵中m01，m10分别代表着s光或者p光的振幅衰减，正的代表s光振幅衰减，负的代表p光振幅衰减；同时Mueller矩阵的矩阵元中m23和m32分别代表s光的位相延迟和p 光的位相延迟［11］。

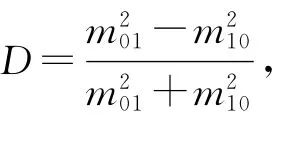
对于路径1：

其双向衰减率为：

位相延迟差为：

对于路径2：

其双向衰减率为：

位相延迟差为：

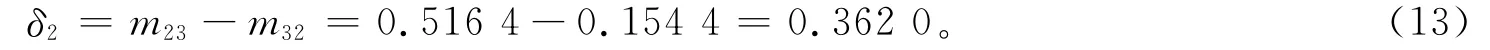
在线偏振光入射时，D0＝1，δ0＝0［14］，而经过斯密特棱镜后，其双向衰减率和位相延迟差不再相等，即D1＝0.625 5与D0＝0，δ1＝0.502 6与δ0＝0；D2＝－0.665 3与D0＝0，δ2＝0.362 0与δ0＝0不再相等，由此可以知道：经过棱镜后对其偏振态发生了变化，即产生了偏振像差，因此，只要Mueller矩阵中16个矩阵元的4个矩阵元m01，m10，m23，m32，就可以确定经过斯密特棱镜两路径光的偏振发生了变化，由于两路径的振幅衰减和位相延迟差均不相等，那么，用Mueller矩阵元可以快速地检测出偏振特性发生了变化，即产生了偏振像差。

已知斯密特棱镜两路径的Jones矩阵为［1］：

在文献［1］中用Jones矩阵与入射光的Jones矢量相结合，分析出射光的偏振特性，说明线偏振光入射斯密特棱镜后，出射光不再是线偏振光，而是椭圆偏振光，其偏振特性发生了改变，即产生偏振像差。

3 结 论

用傅里叶级数法确定斯密特棱镜Mueller矩阵的矩阵元，由矩阵元计算出两路偏振光的双向衰减率和位相延迟差均不相同，说明经过斯密特棱镜后，光线的偏振特性发生了变化，产生了偏振像差。该方法与斯托克斯参量法相比，只与斯密特棱镜本身特性有关，不再与入射光的偏振态有关。与用Jones矩阵相比用，Mueller矩阵分析偏振特性更加简单明了。因此，对斯密特棱镜的偏振特性用Mueller矩阵法分析和检测是既直观又便捷的好方法。

［1］ LU J J，YUAN Q，SUN X P，et al.Research of the polarization aberration on Smith prism［J］.Physics Procedia，2011，19：447－455.

［2］ 卢进军，孙雪平，李向阳.偏振和衍射双重效应影响的Schmidt棱镜特性［J］.光子学报，2012，32（5）：36－42.

［3］ 杨晓翠.完全偏振光系统的Jones矩阵方法［J］.通化师范学院学报，2005，26（6）：39－40.

［4］ 梁铨廷.偏振器件的琼斯矩阵［J］.光学仪器，1988，10（4）：1－9.

［5］ ICHMOTO K，SHINODA K，YAMAMOTO T，et al.Photopolarimetric measurement system of mueller matrix with dual rotating waveplates［J］.Publ Natl Astron Obs Japan，2006，9：11－19.

［6］ 李雅男，孙晓兵，乔延利，等.铝板的偏振反射Mueller矩阵实验研究［J］.大气与环境光学学报，2010，5（3）：203－208.

［7］ 幸 翀，赖晓涛，王 楠，等.混浊介质后向散射特性的Mueller矩阵实验测量［J］.生物物理学报，2008，24（1）：77－82.

［8］ KYEA J，MCINTYREB G，NORIHIROC Y，et al.Polarization aberration analysis in optical lithography systems［J］.Optical Microlithography，2006，36（7）：1553－1559.

［9］ 张 颖，李 林，黄一帆.光学系统的偏振像差分析［J］.光学技术，2005，31（2）：202－207.

［10］ CHENAULT D B，PEZZANITI J L，CHIPMAN R A.Mueller matrix algorithms［J］.Polarization Analysis and Measurement，1992，1746：231－246.

［11］ PEZZANITI J L，CHIPMAN R A.Mueller matrix imaging polarimetry［J］.Optical Engineering，1995，34（6）：1558－1568.

［12］ YUN G，CRABTREE K，CHIPMAN R A.Three－dimensional polarization ray tracing and diattenuation calculation［J］.SPIE OSA，2010，7652：76521X1－76521X7.

［13］ YUN G，CHIPMAN R A.Three－dimensional polarization ray tracing，retardance［J］.SPIE OSA，2010，7652：76521W1－76521W7.

［14］ 李旸晖，沈伟东，章岳光，等.基于Jones矩阵的薄膜诱导偏振像差分析［J］.光学学报，2010，30（12）：

s100109－1－s100109－4.