基片衍射时原子速率对激光汇聚铬原子沉积的影响

张宝武，支理想，张文涛，贾梦翔

（1.中国计量学院计量测试工程学院，杭州310018；2.桂林电子科技大学电子工程学院，桂林541004）

基片衍射时原子速率对激光汇聚铬原子沉积的影响

张宝武1，支理想1，张文涛2，贾梦翔1

（1.中国计量学院计量测试工程学院，杭州310018；2.桂林电子科技大学电子工程学院，桂林541004）

为了研究基片衍射对激光汇聚原子沉积的影响，基于标量光学衍射理论，采用数值计算对比分析了基片衍射与否两种情况下，铬原子波包几率密度分布（表征了沉积条纹）特征值随原子波包速率的变化。结果表明，当原子波包横向速率保持不变、而纵向最可几速率在考察范围内变化时，基片衍射会使波包几率分布的最大值平均约有14.9％的增加量，而半峰全宽平均约有14.3％的减小量；当原子波包纵向最可几速率保持不变、而横向速率在考察范围内变化时，基片衍射会使波包几率密度分布的最大值平均约有14.5％的增加量，而半峰全宽平均约有16.9％的减小量。该研究成果为实验提供了有益的理论指导。

激光技术；基片衍射；原子波包；光学势阱

引 言

激光汇聚铬原子沉积1维纳米光栅样板技术在国家纳米技术产业发展中具有非常重要的地位，它为纳米测量仪器、纳米尺度器件的研究以及开发中纳米尺寸长度的精确测量问题的解决提供了一条崭新的思路，将对开发新型纳米和微米结构标准尺寸元件起到极大的推动作用。相关的研究结果显示，利用激光驻波场汇聚铬原子束沉积获得的1维纳米光栅结构可以用作原子力显微镜等纳米测量工具的计量标准［1-2］。其主要原因在于这种技术使用的激光频率直接锁定在铬原子共振跃迁频率上，汇聚沉积的纳米光栅结构在10-5量级上很好地复现了激光驻波场周期［2］。不过这些研究同时指出，虽然这种纳米光栅结构的平均节距非常准确，但是在一个栅格线对上的单次测量会产生很大的不确定性，其主要的原因是目前制造的样品沉积线比较粗，这将限制它在某些场合的应用，例如作为线宽标准。为此，国内外众多研究小组首先从理论上进行了条纹精细化的探讨。至今，描述这种光刻技术的模型有经典粒子模型［3］和量子波动模型［4］；原子射入汇聚驻波场的初始状态的均匀分布选取方法［5］和蒙特卡罗随机选取方法［6］；平面1维仿真［3，5］和3维仿真［7］；高斯激光驻波场模型［3-4］和椭圆型驻波场模型［8］等等。这些研究一定程度上反映了上述各种参量对原子光栅精细化的影响，但是这些理论结果都存在一个共同的不足之处，就是在考虑基片这个参量的时候，没有考虑基片边缘对汇聚激光场的衍射效应，因此，也就没有考虑这种衍射效应对沉积条纹特性的影响。为此，参考文献［9］和参考文献［10］中从直边衍射物理模型入手，对比讨论了基片衍射与否两种情况下高斯激光驻波场及其光学势阱的特性。在此基础上，作者通过数值计算进一步研究了特定激光参量，即不同原子纵向速率和横向速率情况下，基片衍射对沉积条纹（用原子波包几率密度分布来表征）的最大值和半峰全宽（full width halfmaximum，FWHM）的影响。

1 理论分析

如图1所示，为了获得对比度好、能够准确反映激光驻波场光学势阱周期的纳米光栅，实验中一般要求入射激光束的中轴线正好位于基片表面内，并且和基片上表面严格平行，即汇聚激光束被基片沿轴切掉一半。如图坐标，铬原子束沿着z轴自上往下传输，汇聚激光束沿着x轴自左向右传播。图1中K表示激光和基片刚刚相遇时的垂轴截面，定义为衍射屏（坐标为y1-O1-z1），F表示镜面所在的平面，E表示K和F之间垂直于激光中轴线的某一个考察平面（坐标为y-O-z）。整个系统的x轴原点设置在反射镜所在平面处，坐标z1和z相互平行，并且K和F两个平面之间的距离记为x0，E和F两个平面之间的距离记为x。

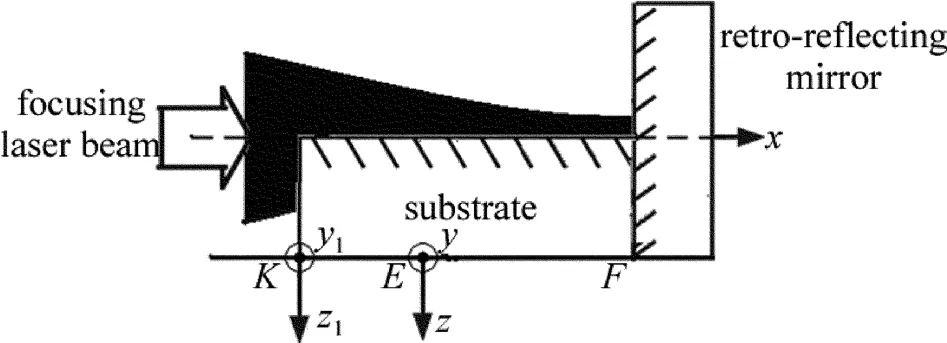
Fig.1 Relative positions of laser，substrate and retro-reflectingmirror

［9］中的理论分析可知，入射激光和其自身反射激光在考察面E上某一点P的复振幅E˜1（P）和E˜2（P）分别为：

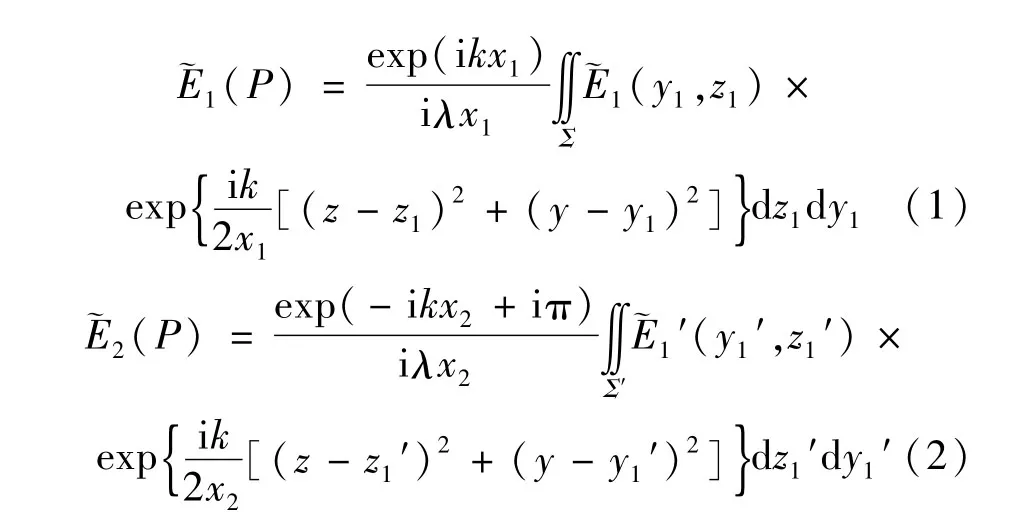
式中，i是虚数单位；k=2π/λ是光波波数，λ是光波波长；积分区域覆盖基片表面之上所有透光区Σ：y1⊂［-∞，∞］，z1⊂［-∞，0］；（x0，y1，z1）为入射激光起初衍射的任意一点Q的坐标，其复振幅记为˜E1（y1，z1），Q点相对于反射镜的镜像Q′必然是反射波的起始衍射点，其坐标记为（-x0，y1′，z1′），复振幅记为˜E1′（y1′，z1′）。如此，则考察平面上（x，y，z）位置处的P点分别与Q点和Q′点之间的垂直距离为x1=x-x0和x2=x+x0。这样，入射行波场和反射行波场相遇叠加后就会形成驻波场，其光强表达式为：

I（P）=［˜E1（P）+˜E2（P）］［˜E1（P）+˜E2（P）］*（3）式中，*表示共轭。将（3）式代入到汇聚原子的光势阱表达式［11］中，可以得到衍射情况下激光驻波势阱表达式：

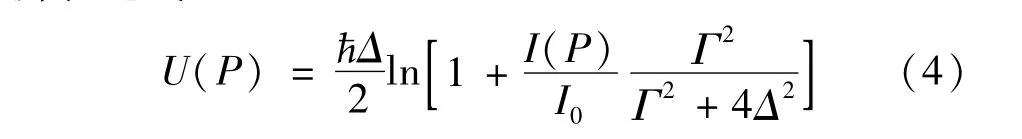
式中，ħ为除以2π的普朗克常数，Δ为激光频率失谐量，Γ是原子跃迁的自然线宽，I0为原子跃迁的饱和强度。

按de Broglie关系，可以假定沿z轴方向传输的铬原子束对应的是一个平面波，原子在某一时刻出现在某一位置附近的几率分布在x方向上为一个高斯分布的波包［4］，其中心沿z方向具有一定的初始平均动量，则在坐标表象内波函数（记入时间相关因子）为：

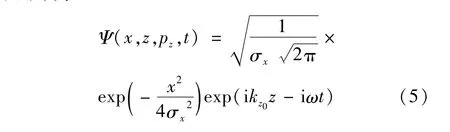
式中，σx为x方向上原子波包的初始宽度；kz0为原子波包传播的波数；ω为原子波包传播频率；t为波包传播时间。

参考文献［4］中详细推导了汇聚激光驻波场中原子波函数演化过程中满足的定态薛定谔方程，即：

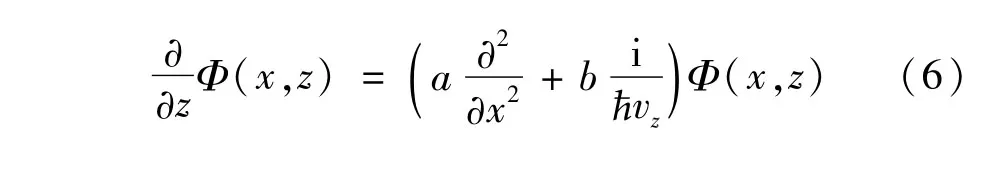
2 模拟结果和讨论

图2是激光驻波场形成光学势阱的俯视图，其中，基片表面位于z方向上0位置处，反射镜表面位于x方向上0位置处。图2a是衍射时的情况，图2b是非衍射时的情况。从图2中可以清楚地看出基片衍射对光学势阱的影响：在光轴方向上，衍射与否不会影响光学势阱形成驻波的特性；在垂直光轴方向上，衍射存在与否不影响光学势阱高斯分布的轮廓线特征，但是会使光学势阱产生强度的振荡，与此同时会使衍射情况的最大值向着原子束源方向移动，且略大于非衍射情况下的最大值。

Fig.2 Vertical view of optical potential of laser standing wave

在图2所示光学势阱中，原子波包几率密度沿着x=-0.25λ这条线在z轴方向的变化情况如图3所示，其中还清晰地给出了这条线上光学势阱的轮廓线。仿真过程中原子波包纵向平均速率为960m/s，横向速率为153.6mm/s（对应的发散角为.16mrad）。图3显示，基片会对光学势阱产生衍射，使之在z轴方向上出现一定的振荡，使其最大值有所提高的同时还会发生一定的位移（图3中z= -50μm位置处）。这样的结果就使得原子波包的几率密度相对于非衍射情况下有所提高（图3中z =0位置处）。这种变化情况可以由基片表面位置处x方向上原子波包几率密度分布来充分地显示，如图4所示，其中同时给出了光学势阱在这个平面内沿激光轴的强度分布。图4显示，衍射与否两种情况下原子波包几率密度分布轮廓（这表征了沉积条纹）有明显区别：衍射光学势阱会提高原子波包几率密度分布的中心值，使之变为非衍射情况下的1.14倍，减小原子波包几率密度分布的半峰全宽，使之变为非衍射情况下的0.82倍。

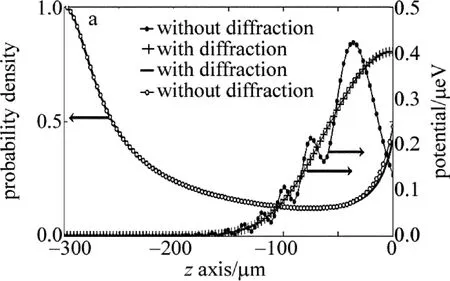
Fig.3 Evolution of atom wave-packet before and after optical potential

Fig.4 Probability desity distribution of the atom wave-packet in x direction

图5中给出了衍射与否两种情况下，基片表面原子波包几率密度分布的最大值和半峰全宽随纵向最可几速率的变化，其中横向速率保持153.6mm/s不变。

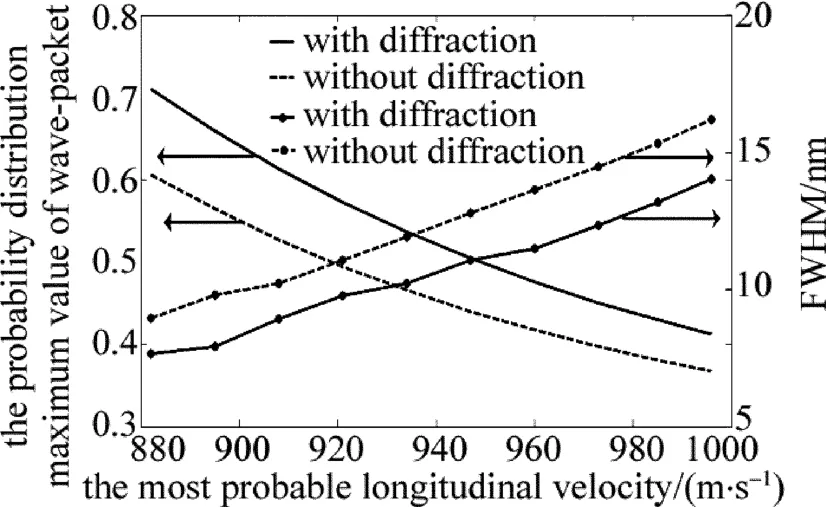
Fig.5 Relationship between the probability distribution max value of wave-packel or FWHM and themost probable longitudinal velocity

从图5中可以看出，不管基片衍射与否，在考察范围之内，纵向最可几速率的变化都会影响沉积条纹特征值：原子波包几率密度分布的最大值会线性地随着纵向最可几速率的增大而减小，而半峰全宽会随之线性地增加。不过，和非衍射情况相比，基片衍射时，同一个纵向最可几速率位置处，原子波包几率密度分布中心最大值平均约有14.9％的增加量，而其半峰全宽平均约有14.3％的减小量。

图6中给出了衍射与否两种情况下，基片表面原子波包几率密度分布中心最大值和半峰全宽随横向速率的变化，其中纵向速率保持960m/s不变。

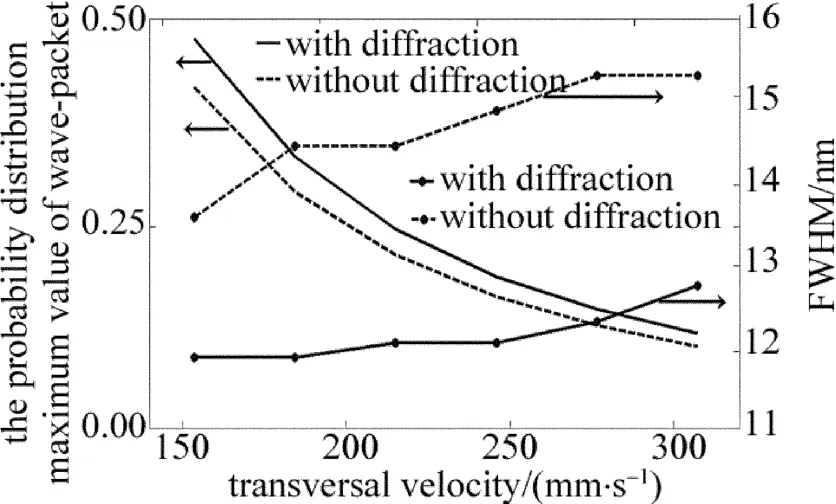
Fig.6 Relationship between the probability distribution max value of wave-packet or FWHM and transverse velocity

从图6中可以看出，不管基片衍射与否，在考察范围之内，横向速率的变化都会影响原子波包几率密度分布的特征值：原子波包几率分布的最大值会随着横向速率的增大而线性地减小，而其半峰全宽会随之增大。不过，和非衍射情况相比，基片衍射时，每一个横向速率位置处，原子波包几率密度分布的最大值平均约有14.5％的增加量，而其半峰全宽平均约有16.9％的减小量。

3 结 论

基于标量光学衍射理论，理论分析了激光汇聚铬原子沉积技术中基片对汇聚激光场的衍射情况，以原子波包理论为基础进一步分析了基片衍射影响与否两种情况下，铬原子波包几率密度分布的特征值随原子波包纵向最可几速率和横向速率的变化情况。仿真结果充分显示了基片衍射对原子波包几率密度分布的特征值的影响：和非衍射情况相比，基片衍射会提高原子波包几率密度分布的最大值，减小其半峰全宽。该研究结果为实验提供了更加丰富的理论指导。

参考文献

［1］LIT B.Nanometrology and transfer standard［J］.ShanghaiMeasurement and Testing，2005，32（1）：8-13（in Chinese）.

［2］McCLELLAND J J，ANDERSONW R，BRADLEY C C，et al.Accuracy of nanoscale pith standards fabribcated by laser-focused atomic deposition［J］.Journal of Research of the National Institute of Standards and Technology，2003，108（2）：99-113.

［3］McCLELLAND J J.Atom-optical properties of a standing-wave light field［J］.Journal of the Optical Society of America，1995，B12（10）：1761-1767.

［4］KIDAN T，ADLER J，RON A.Numerical simulations of an atomic beam focused by an optical potential［J］.Computers in Physics，1998，12（5）：471-477.

［5］ZHANGW T，ZHU BH，XIONGXM，etal.Characteristicsof deposition for neutral atoms in laser standingwavewith different velocities［J］.Acta Physica Sinica，2011，60（6）：063202（in Chinese）.

［6］ZHANG PP，MA Y，LIT B.Optimization of particle opticsmodel for one-dimensional atom lithography［J］.Acta Optica Sinica，2011，31（5）：0514004（in Chinese）.

［7］ZHANG BW，MA Y，ZHAO M，et al.3-D simulation of nano-grating by Cr atom beam deposition［J］.Laser Technology，2011，35（3）：364-367（in Chinese）.

［8］ZHANGW T，ZHU B H，HUANG J，etal.Chromium atom deposition in elliptical standing wave field［J］.Acta Physica Sinica，2011，60（10）：103203（in Chinese）.

［9］ZHANG BW，MA Y，ZHANG P P，et al.Simulations of Gaussian laser standingwave based on diffraction by straightedge［J］.Laser Technology，2012，36（6）：810-813（in Chinese）.

［10］ZHANG BW，ZHIL X，ZHANGW T.Simulations of optical potential formed resulted from Gaussian laser standing wave based on diffraction by straight edge［J］.Acta Physica Sinica，2012，61（18）：183201（in Chinese）.

［11］ANDERSONW R，BRADLEY C C，McCLELLAND J J，et al.Minimizing feature width in atom optically fabricated chromium nanostructures［J］.Physical Review，1999，A59（3）：2476.

Effect of atom ic velocity at substrate diffraction on laser-focused Cr atom deposition

ZHANG Bao-wu1，ZHILi-xiang1，ZHANGWen-tao2，JIAMeng-xiang1
（1.College of Metrology＆Measurement Engineering，China Jiliang University，Hangzhou 310018，China；2.College of E-lectronic Engineering，Guilin University of Electronic Technology，Guilin 541004，China）

In order to study the effect of substrate diffraction on laser-focused Cr atom deposition，simulation and comparative analysis were performed based on the scalar optical diffraction theory under the presence and absence of substrate diffraction.The variation of stripe value of atomic wave-packet probability distribution which stands for the deposited lines with different atomic wave-packet velocities was focused.The results show that because of substrate diffraction，themax value of wave-packet probability distribution has 14.9％average increase and the full width of half maximum（FWHM）has14.3％average decrease for different longitudinalmost probable velocitieswhen transverse velocity remains constant；themax value of wave-packet probability distribution has 14.5％average increase and the FWHM has 16.9％average decrease for different transverse velocities when themost probable longitudinal velocity remains constant.The research results provide a richer theoretical guidance for the experiment.

laser technique；substrate diffraction；atomic wave-packet；optical potential

O43

A

10.7510/jgjs.issn.1001-3806.2013.04.002

1001-3806（2013）04-0421-04

国家自然科学基金资助项目（10972210；11064002）；浙江省钱江人才计划资助项目（2011R10094）；浙江省自然科学基金资助项目（LQ12E05018）；广西省自然科学基金资助项目（2012gxnsfaa53229）

张宝武（1978-），男，博士，讲师，研究方向为原子光刻技术。

E-mail：zhangbaowu1978＠gmail.com

2012-12-01；

2013-01-05