基于特征加权支持向量机的武器系统效能评定方法

李景熹，蒋铁军

(1.海军装备部 舰船办，北京 100071;2.海军工程大学装备经济管理系，湖北 武汉 430033）

基于特征加权支持向量机的武器系统效能评定方法

李景熹1，蒋铁军2

(1.海军装备部 舰船办，北京 100071;2.海军工程大学装备经济管理系，湖北 武汉 430033）

针对武器系统效能综合评定的任务需求，同时考虑到传统特征选择方法的不足，提出采用一种监督型封装模式的加权特征选择方法用于武器系统的效能评定，能有效区分不同特征对效能的影响程度。鉴于支持向量机的良好应用效果以及混合核函数的优良性能，采用基于混合核函数的支持向量机建立特征与效能之间的关系模型。考虑到特征选择和评估模型建立的目标一致性，提出一种基于粒子群优化算法的联合优化方法，同时实现特征的影响程度分析和效能评估模型的优化。最后以导弹系统的效能评定问题为背景开展应用分析，实际计算表明所提出方法的有效性。

效能评定;加权特征选择;支持向量机;混合核函数;粒子群优化算法

0 引言

在武器系统的研制、试验、采购、使用及维修等各个阶段，其效能的综合评定都显得十分重要，是武器系统管理必不可少的有效工具。

对于武器系统的效能评定，目前有许多方法可供采用，如专家评定法、试验统计法、作战模拟法、指数法、解析法、参数效能法等［1］。其中，指数法和参数效能法通过建立效能和各项指标之间的关系式对效能进行评定。通过关系式的建立，一方面能够实现对武器系统效能的综合评定，另一方面还能够确定各项指标对效能的影响程度，这一点对于获取提升武器系统效能的方案尤为重要;同时，这类方法还具有结构简单、使用方便的特点，因此，在实践中得到了广泛的应用。

一般来说，为避免信息的丢失，在建立战术技术指标与效能之间的关系时，通常会尽可能多地收集影响效能的战技指标或称为特征参数。但在很多情况下，影响系统效能的特征参数是很多的。例如对于导弹系统而言，可能涉及到的影响因素包括发射重量G0、导弹长度L、导弹翼展长度E、导弹的最大飞行速度Mmax、最大射高Hmax、导弹最大直径dmax、战斗部重量Gz、最大射程Rmax和杀伤概率P等［2］。针对这种情况建立模型时，引入无关特征往往会降低关系式的推广应用效果，同时也给收集数据带来困难，当样本量比较小时 (如武器系统领域）尤为突出。因此，需要在建立评估模型前对特征进行筛选，一方面得到效果比较好的效能评估模型，另一方面实现对指标重要性的判别。

通常用于将多个指标化为少数指标的方法有主成分分析和Rough集等。主成分分析通过对原始指标集进行空间转换实现指标的综合，但是通常比较适合指标间相互独立或呈线性关系的情况，而且提取得到的主成分通常不具有明确的物理意义，不便于后续的分析;Rough集能够对战术技术指标进行有效筛选，但是需要制定阈值对各项指标进行简约，而且对指标集的简约或多或少会存在信息的损失［3］。

本文提出一种基于监督型封装模式的加权特征选择方法，用于武器系统效能的综合评定，通过加权，可以更加细致地区分特征对评估性能的影响情况以提高评估模型的效果，进而有效解决效能的综合评定问题。

1 效能评估模型的建立

1.1 监督型的特征选择

监督型的特征选择方法一般分为过滤模式和封装模式2种，如图1所示。

1）过滤模式。在过滤模式中，特征选择只是作为一种预处理手段，分析对象是候选特征子集及其数据，它不直接优化任何特定的预测模型。特征选择的过程与模型建立的过程无关，它们独立分步地完成。

2）封装模式。在封装模式中，选择方法在进行初步的特征选择以后，还要通过这些特征建立评定模型，根据其评定的效果对选择的特征子集实施评估。封装模式把特征选择看作是在所建立的评价准则下对特征空间中所有可能的组合进行搜索的问题［4］。

图1 特征选择中的过滤模式和封装模式Fig.1 Filtermode and wrappermode in feature selection

1.2 效能评定模型

支持向量机 (support vector machine，SVM）是一种基于统计学习理论和核技术而建立的新型机器学习方法，由于其对小样本问题的适应能力及良好的泛化推广性能，已经得到较为广泛的应用［5－8］。

本文采用SVM描述战术技术指标与效能之间的关系，建立武器系统效能评估模型;同时，考虑到核函数对SVM模型性能的重要性，选取应用效果较好的混合核函数作为SVM的核函数，并与RBF核以及多项式核进行对比。

混合核函数的形式为［9－10］

式中:Kpoly为多项式核函数;Krbf为RBF核函数。对于输入空间的不同区域，混合核系数的特征由不同的ρ所决定。ρ为一个向量。通过引入混合核系数，不同核对模型的相对贡献可以通过系数来加以调节。在本文中，对于整个输入空间采用统一的核系数ρ。

2 特征选择中的联合优化方法

封装模式的特征选择涉及到特征子集的选择和评估模型的确定。在以往的特征选择研究中，通常将特征选择与模型确定分开，即先进行特征的优化选择，然后再进行模型的确定，实质上是一种分步优化的方法。但实际上，在封装模式下，当选择优化的特征子集时，优化的评估模型也就建立了起来，二者的优化过程是相互影响的。因此，考虑到封装模式进行特征选择的特点，本文提出一种联合优化的方法，即将特征的选择以及评估模型的确定同时进行。

鉴于粒子群优化 (particle swarm optimization，PSO）算法所具有的个体数目少、计算简单、鲁棒性好、容易实现并且没有许多参数需要调整等诸多优势［11］，及其在函数优化、神经网络训练、模糊系统控制等许多领域的广泛应用［12－15］，本文采用PSO算法在一个共同的目标下实施联合优化，同时完成特征的选择和模型的优化。运用PSO算法确定特征子集和评估模型的关键问题是定义自变量和目标函数 (适应度函数）。

2.1 自变量的定义

由于需要联合优化特征和评估模型，因此，对于自变量的设定采用一种混合的形式，即同时包含特征和模型参数。

2.1.1 传统的特征选择

对于传统的特征选择方法，设定特征为离散变量0或1，如果第i个特征为1，则表示该特征被选中，否则这个特征就被舍弃。

评估模型的参数与SVM以及核函数的类型有关，其取值对于学习能力和推广能力都有很大的影响。对于SVM，其损失函数选取为ε不敏感损失函数，具体形式为

因此，对于基于混合核函数的SVM模型，其参数包括正则化参数γ、不敏感参数ε、多项式核中的多项式阶数d、RBF核中的参数σ2以及混合核系数ρ。

这些参数对模型的性能起着至关重要的影响。

2.1.2 加权特征选择

对于加权特征选择，此时的自变量集由特征1权重、特征2权重，…，特征p权重，以及正则化参数γ，不敏感参数ε，多项式核参数d，RBF核参数σ2，混合核系数ρ等模型参数组成。

加权特征选择中，特征的选取不再是简单的0或1，而是介于0～1之间的某个权值。由此可以看出，通常所进行的特征选择只是加权特征选择方法的一种特殊情况。采用连续的PSO算法就可以联合优化实现特征的加权选择和评估模型的优化。

2.2 适应度的定义

适应度用来描述在被选特征子集下所建立的评估模型的性能。在确定了特征子集以后，就可以选参数γ是在结构风险和样本误差之间作出折衷，参数γ的取值与可容忍的误差相关，较大的γ值允许较小的误差，较小的γ值则允许较大的误差。不敏感参数ε则与噪声水平相关，其取值一般与噪声水平成比例关系，较小的ε能够使SVM对数据的逼近效果非常好，但是容易造成过度拟合，使得模型在推广应用时存在很大的风险;较大的ε推广应用的风险较小，但是模型对现有数据的拟合能力较差，对现有数据的规律体现得不够。核函数中参数的取值直接决定了数据转换后特征空间的特性［10］。因此，需要根据实际情况进行优化选择。

特征选择时，联合优化的自变量集由特征1，特征2，…，特征p;正则化参数γ，不敏感参数ε，多项式核参数d，RBF核参数σ2及混合核系数ρ等组成。具体的数值更新采用二进制PSO算法和连续PSO算法混合进行。评估模型中相关参数的取值范围需要根据经验设定。

连续PSO算法在文献 ［16］中有详细描述。对于二进制PSO算法，与连续PSO算法类似，每个粒子表示长度为p的二进制向量的值，速度更新公式保持不变，而位置更新采用下式进行:择适当的数据作为样本建立评估模型了。为充分提高所建立模型的泛化能力，采用L折交叉验证的方式来评价训练的效果，对于测试样本集的评价，所采用的指标为均方根误差 (rootofmean square error，RMSE），具体表达式为

3 应用分析

3.1 数据选取

为说明方法的有效性，本文选取文献［3］中的有关数据，针对导弹武器系统的效能评定问题展开研究，几种导弹的特征参数与系统效能如表1所示。

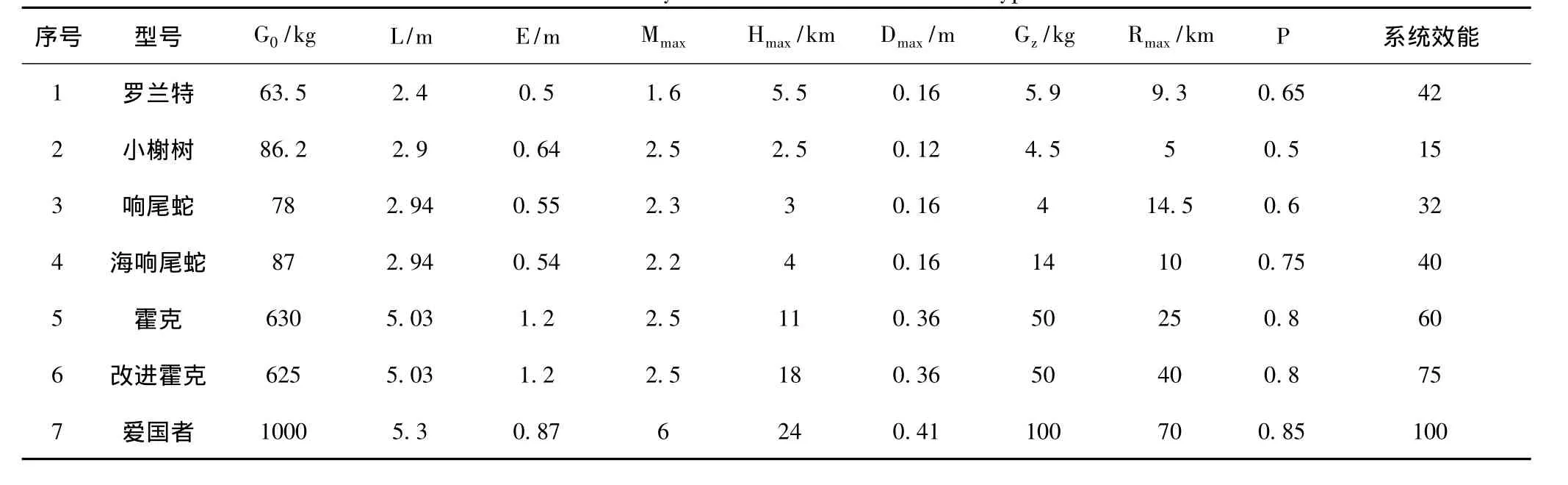
表1 几种导弹的参数和系统效能Tab.1 Parameters and system effectiveness of several types ofmissiles

3.2 参数设置

为了与不实施特征选择时建模的效果进行对比分析，本文对模型建立中的各种参数采用统一的设置。参数范围统一设置为:γ∈［0.001 100］;d∈［0.001 12］;σ2∈［0.001 3 000］;ρ∈［0.001 1］;ε∈［0.001 0.02］。

PSO算法中:粒子最大速度Vmax=20;总粒子数为τ=20;加速因子c1=c2=5;惯性因子ω从0.9随着迭代次数的增加线性递减到0.4;最大迭代次数100。考虑到PSO算法的随机性，按照设定的情况计算20次，取其中效果最好的1次作为训练结果。

3.3 计算分析

本文针对全部特征、特征选择和加权特征选择3种情况分别建立评价模型，采用PSO算法对模型进行优化，计算得到的优化结果如表2所示。3种情况下评价模型的优化收敛过程如图1所示。

表2 模型优化结果Tab.2 Model optimization results

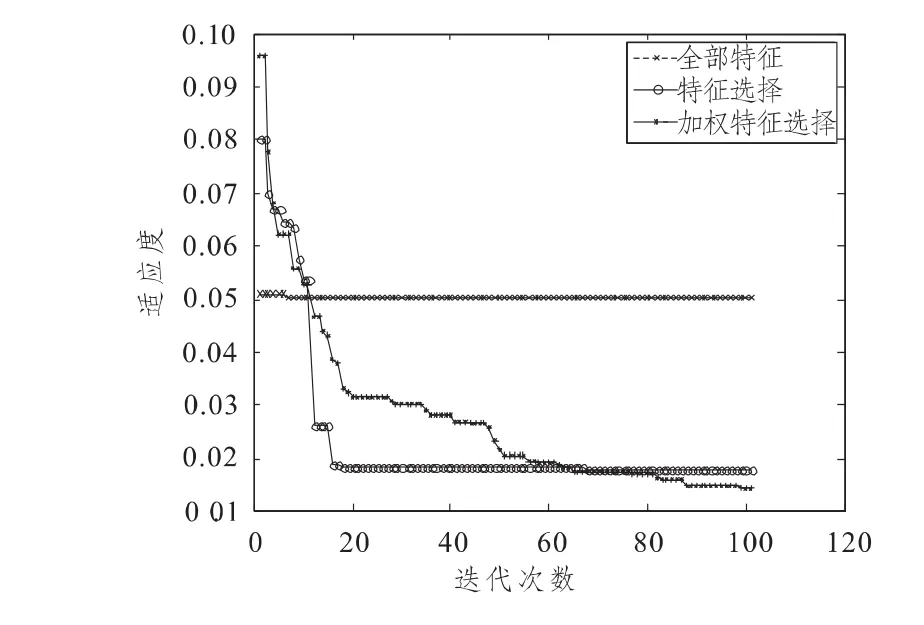
图3 三种不同情况下模型优化的收敛情况Fig.3 Model optimization convergences in three different situations

从计算结果可以看出:

1）全部特征与特征选择

特征选择的计算结果略优于全部特征的结果，而且模型优化的收敛效果也更好，通过选择得到的特征也可以看出，特征选择较全部特征时重点更为明确，对导弹武器系统效能影响较大的指标是:导弹长度L、最大射高Hmax、导弹最大直径dmax、最大射程Rmax和杀伤概率P。因此，为了能够较好地提高武器系统的综合效能，在论证设计时应该重点从这几个指标加以权衡考虑。

2）特征选择和加权特征选择

加权特征选择的计算结果则明显优化全部特征和特征选择时的情况，而且模型优化收敛的效果也非常好，表明从建模计算的角度，加权特征选择有非常明显的优势。从实际应用的角度来看，加权特征选择不是简单地对特征进行取舍，而是得出了各个指标的权重或称重要程度，具体排序情况是6＞5＞8＞2＞9＞3＞1＞4＞7。排在前面的5个特征就是通过特征选择方法得到的5个特征，最终结果一致，但是相对于特征选择方法而言，计算结果更为细致，得出的结果能够反映出更多的信息，也更有利于武器系统效能评定的实际应用。

为了更加有力地验证方法的有效性，本文在文献［3］的基础上，将几种常用方法进行对比，具体对比结果如表3所示。

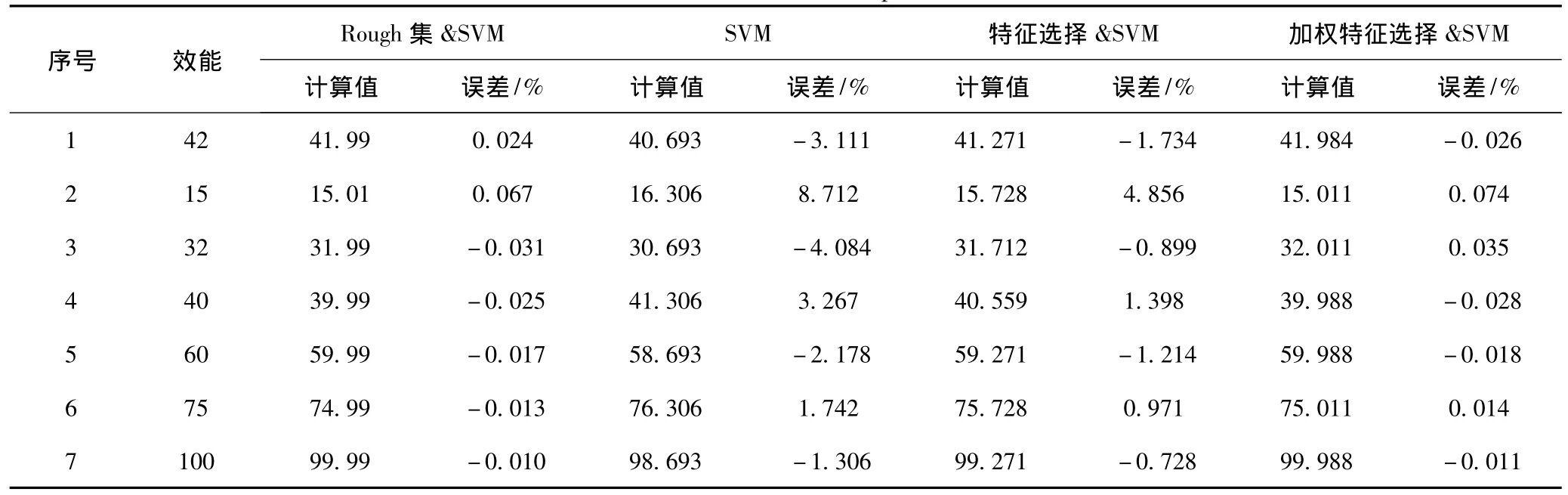
表3 几种常用效能评定方法的对比计算结果Tab.3 Calculation resultswith several common performance assessmentmethods

从表中的计算数据可以看出，Rough集＆SVM方法所建立的模型较采用所有特征时建立的模型效果更好，由于这种处理方法将特征处理与模型构建分离开来，虽然能够获得较好的拟合结果，但存在一定的特征信息丢失，而且对于所得到的特征集也无法进一步区分;采用加权特征选择方法对样本的评估精度与Rough集＆SVM方法相当，但是该方法充分利用了所选取特征的信息，而且对不同特征作出重要程度的区分，比较符合实际工作需求。

4 结语

本文提出一种基于特征加权的武器系统效能综合评定方法，不仅能够得到战术技术指标与效能之间的关系用于效能评估，而且能够区分各种战术技术指标对效能的影响程度，满足武器系统效能综合评定的需求，所提出的联合优化方法能够同时实现特征的选择和模型的优化，应用计算表明该方法的实践效果优于传统的特征选择方法。

该方法能够取得比较好的效果，但是也存在一定不足:由于方法实施过程中是采用进化算法迭代进而获取优化的效能评估模型，计算量较其他方法要大，尤其是当交叉验证折数较大时。因此，今后的一个研究重点是对现有优化算法进一步改进，使得能够高效地得到满意的结果。

［1］高尚，娄寿春.武器系统效能评定方法综述［J］.系统工程理论与实践，1998(7）:109－114.

GAO Shang，LOU Shou-chun.Summary of weapon system effectiveness evaluation method［J］.Systems Engineering Theory and Practice，1998(7）:109 －114.

［2］文仲辉.导弹系统分析与设计［M］.北京:北京理工大学出版社，1989.

WEN Zhong-hui.Missile systems analysis and design［M］.Beijing:Beijing Institute of Technology Press，1989.

［3］高尚，房靖.基于粗糙集和支持向量机的效能评定［J］.系统工程与电子技术，2008，30(7）:1291－1294.

GAO Shang，FANG Jing.Performance assessment based on rough sets and support vector machine［J］.Systems Engineering and Electronics，2008，30(7）:1291 －1294.

［4］KOHAVI R，JOHN G H.Wrappers for feature subset selection［J］.Artificial Intelligence，1997，97(1 － 2）:273－324.

［5］朱丽华.基于粗糙集和C－均值聚类支持向量机的员工绩效评估方法［J］.价值工程，2009，28(11）:1 －4.

ZHU Li-hua.The performance evaluating method of employee based on rough set and C-means clustering support vector machine［J］.Value Engineering，2009，28(11）:1－4.

［6］吴冲，夏晗.基于五级分类支持向量机集成的商业银行信用风险评估模型研究［J］.预测，2009，28(4）:57－61.

WU Chong，XIA Han.Credit risk assessment in commercial banks on five-class support vectormachines ensemble［J］.Forecasting，2009，28(4）:57 －61.

［7］孙瑾，许青松，陈燕燕.基于遗传算法和支持向量机的银行个人信用评估［J］.统计与决策，2008(12）:130－134.

SUN Jin，XU Qing-song，CHEN Yan-yan.Bank personal credit rating based on genetic algorithm and support vector machine［J］.Statistics and Decision，2008(12）:130 －134.

［8］张目，周宗放.基于多目标规划和支持向量机的企业信用评估模型［J］.中国软科学，2009(4）:185－190.

ZHANG Mu，ZHOU Zong-fang.An evaluation model for credit risk of enterprise based on multi-objective programming and support vector machines［J］.China Soft Science，2009(4）:185 －190.

［9］MAK B，KWOK J T，HO S.Kernel eigenvoice speaker adaptation［J］.IEEE Transactions on Speech and Audio Processing，2005，13(5）:984 －992.

［10］SMITSG F，JORDAN EM.Improved SVM regression using mixtures of kernels［C］//GirolamiM.Proc.of IJCNN 02 on Neural Networks.Piscataway，NJ:IEEE Press，2002:2785－2790.

［11］KENNEDY J，EBERHART R C.Swarm intelligence［M］.San Francisco:Morgan Kaufmann Publishers，2001.

［12］TSENG C C，HSIEH JG，JENG JH.Active contourmodel via multi－ population particle swarm optimization［J］.Expert Systems with Applications，2009，36(3）:5348－5352.

［13］JIN Ai，VORATAS K.Particle swarm optimization and two solution representations for solving the capacitated vehicle routing problem［J］.Computers ＆ Industrial Engineering，2009，56(1）:380 －387.

［14］ALBERTO G V，RAFAEL P.Introducing dynamic diversity into a discrete particle swarm optimization［J］.Computers＆ Operations Research，2009，36(3）:951 －966.

［15］CLERC M，KENNEDY J.The particle swarm explosion，stability，and convergence in a multidimensional complex space［J］.IEEE Transactions on Evolutionary Computer，2002，6(1）:58 －73.

［16］GUOA YW，LIBW D，MILEHAMA A R，etal.Applications of particle swarm optimization in integrated process planning and scheduling［J］.Robotics and Computer Integrated Manufacturing，2009，25(2）:280 －288.

Assessmentmethod of weapon system effectiveness based on support vector machine with weighted feature

LIJing-xi1，JIANG Tie-jun2
(1.Ship Office of Naval Equipment Department，Beijing 100071，China;2.Department of Equipment Economy Management，Naval University of Engineering，Wuhan 430033，China）

The requirement ofweapon system effectiveness assessment and the importance analysis of tactical and technical indicators were taken into account，moreover，considering the shortcomings of the traditionalmethod of feature selection，A weighted feature selection with the supervised wrapper mode was used in the effectiveness assessment of weapon system，which can effectively distinguish the influence of different features on the system effectiveness.In view of the good application effects of support vector machine(SVM），aswell as a good performance of themixture of kernels，the relationship model among the features and the system effectivenesswas established based on SVM with themixture of kernels.In addition，considering the consistency of feature selection and the establishment of effectiveness assessmentmodel，a joint optimizationmethod based on particle swarm optimization(PSO）was adopted，which can synchronically achieve the influence analysis of features and the optimization of effectiveness assessment model.Experiments show that the proposed method is effective.

effectiveness assessment;weighted feature selection;support vectormachine;mixture of kernels;particle swarm optimization

TK42

A

1672－7649(2013）05－0011－06

10.3404/j.issn.1672－7649.2013.05.003

2012－07－05;

2012－09－26

李景熹(1979－），男，博士，工程师，研究方向为舰船装备总体和装备经济性分析等。