消除EMD边界效应的四中点估计方法

张立振, 刘坦然, 魏恩泊

(1. 中国海洋大学 数学科学学院, 山东 青岛 266100; 2. 中国科学院 海洋研究所, 山东 青岛 266071)

消除EMD边界效应的四中点估计方法

张立振1, 刘坦然1, 魏恩泊2

(1. 中国海洋大学 数学科学学院, 山东 青岛 266100; 2. 中国科学院 海洋研究所, 山东 青岛 266071)

为了快速高效地实现信号的本征模态分解, 消除分解过程中边界效应, 在 Directly-Mean EMD方法的基础上, 通过引入左、右待估中点和左、右延拓中点, 并根据信号首尾两端各种可能的情况给出了四中点估计公式, 建立了可完全消除边界效应的Directly-Mean EMD四中点估计方法。该方法不仅减少了样条插值次数, 提高分解速度, 而且还可以有效避免因插值节点过于稀疏所产生的大幅波动, 使分解结果更加准确。将新方法应用于日长数据序列的本征模态函数分解, 得到了满意的分解结果。

本征模态函数; Directly-Mean EMD方法; 四中点估计方法; 希尔伯特－黄变换; 日长(LOD)

1996年开始, Huang等[1]对HHT(希尔伯特－黄变换)又称 EMD/HSA(经验模态分解与希尔伯特谱分析)进行了系统研究。HHT可以有效地分析非线性、非平稳信号。近几年来, 其应用越来越广泛。分解信号为本征模态函数是 HHT分析中最为关键的一环。Huang给出了信号分解的sifting方法, 这种方法从信号本身的特征尺度出发, 具有很好的自适应性。但是, 在用样条函数拟合信号上、下包络时会出现严重的边界效应, 这将严重影响据此所做出的 Hilbert谱。目前有很多方法来改善边界效应,例如已经向NASA申请专利的特征波法, 黄大吉等[2]给出了镜像闭合延拓法和极值延拓法, 沈路[3]研究了相似极值延拓法, 刘慧婷[4]提出了基于多项式拟合的处理方法, 胡爱军, 孙华刚, 曹冲锋等[5-7]也各自提出了有效的边界处理方法。

Zhong等[8]利用极值点与线性包络的“中点”作为型值点拟合出样条曲线, 将其直接代替 Sifting方法中上、下包络的平均值曲线, 从而建立一种本征模态函数分解的Directly-Mean EMD方法。该方法不仅减少了插值次数, 而且因为增加了型值点数, 使样条曲线的精度得到提高。但是, Zhong等并没有涉及对边界效应的处理, 也没有讨论当信号极值点个数少于4时如何求取中点曲线的问题。本文便是在Directly-Mean EMD方法的基础上, 通过引入左右待估中点和左右延拓中点的概念及其估计方法, 不仅使 Directly-Mean EMD可以完全消除分解时边界效应, 同时针对极值点个数少于4时的各种情况, 给出了中点曲线的求取方法。

1 本征模态函数与Sifting方法

所谓本征模态函数是满足以下两条件的数据集: (1)在整个数据集上, 其极值点的个数和跨零点的个数相同或至多相差为1, 即在相邻的两个上跨零点之间只有一个极大值点和一个极小值点。(2)由极大值点所定义的上包络与由极小值点所定义的下包络的平均值为0。 Huang创立的将信号分解成IMF的sifting方法[1], 基本步骤为首先求出信号的局部极大(小)值点的包络(样条插值)。然后求出上、下包络的平均值,并将其从信号中减掉。重复此操作直至得到本征模态函数, 将此本征模态函数从原信号分离出去。重复上面的操作, 直至剩余信号为只有一个极值点或单调函数为止。

2 Directly-Mean EMD方法

从 Sifting方法的过程可以看到, 在求信号的上下包络时用到了两次样条插值, 然后再求平均值。Directly-Mean EMD方法[8]只用一次样条插值, 具体的方法如下:

步骤 1: 求取信号x(t)的极值点(极大值点和极小值点)。

步骤2: 求取中点曲线。用直线段将极大值点顺次连接起来, 称为信号的线性上包络(图1)。用直线段将极小值点顺次连接起来, 称为信号的线性下包络。每个“▽点”位于“线性上包络”上, 发生的时刻与相应的极小值点一致, 例如“下三角点 D”与相应的极小点C发生在同一时刻。类似地, 每个“△点”位于“线性下包络线”上, 发生的时刻与相应的极大值点一致。设极大值点 A, 极大值点B, 极小值点 C三点的坐标分别为:。容易推出“下三角点 D”的坐标为:

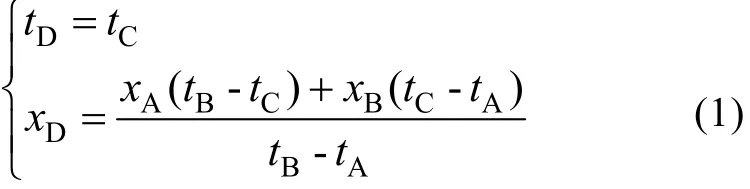
将“下三角点D”与极小值点C连线的中点E称为信号与极小值点C对应的中点, 其坐标为:

每个极值点都可以类似地定义相对应的中点(图1中用o表示的点)。易知用直线段将所有中点连接起来得到的折线恰为上、下线性包络的平均值。由于信号的真实包络不一定正好是线性的, 所以, 将所有中点作为型值点拟合出的样条曲线m1(t)作为真实包络平均值的估计, 并称其为信号的中点曲线。

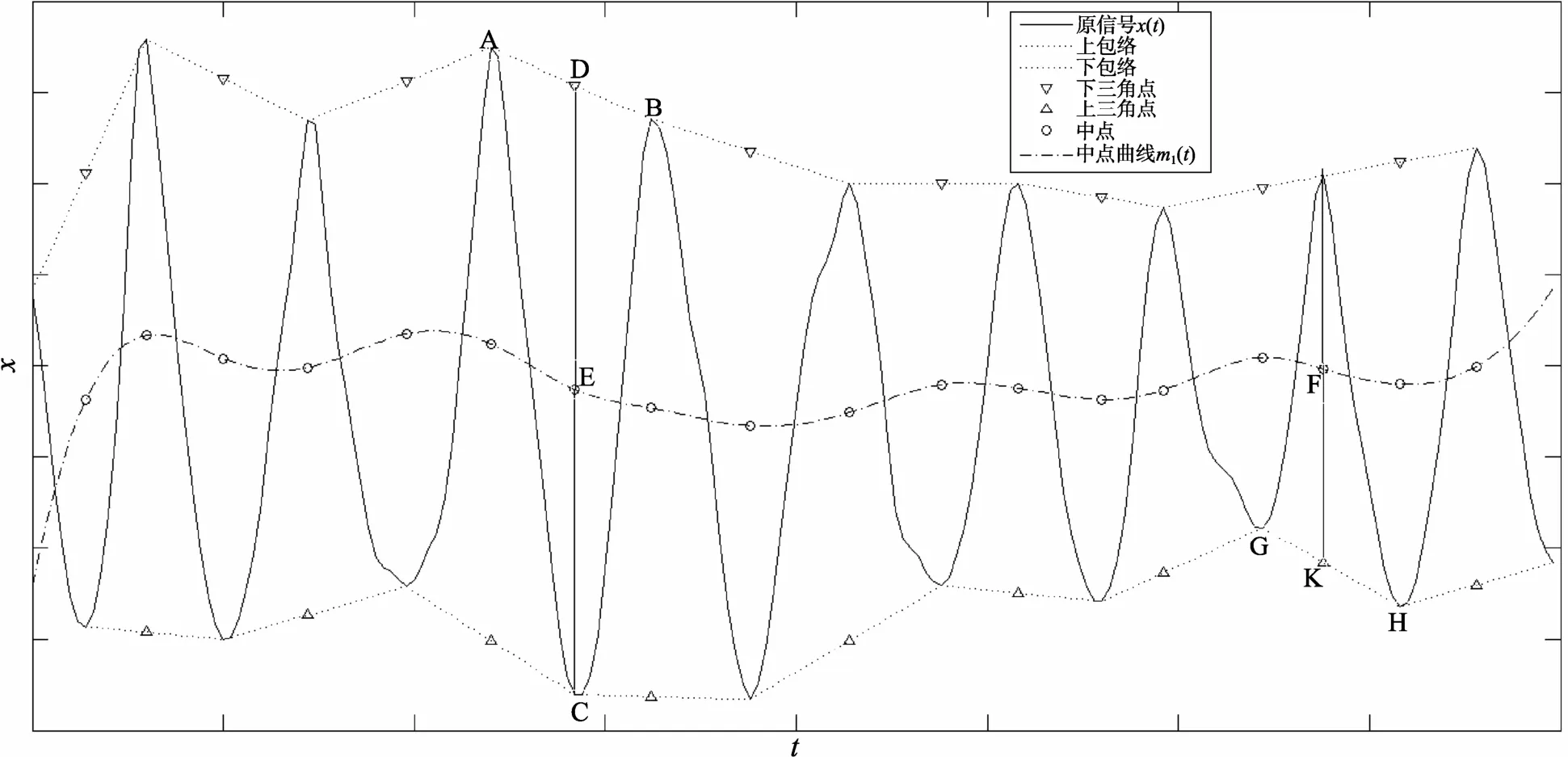
图1 Directly-Mean EMD方法几个主要概念Fig. 1 Important concepts in Directly-Mean EMD method

于是得到x(t)的本征模态函数分解式:

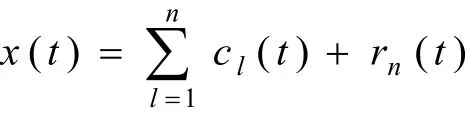
上述分解过程即为Directly-Mean EMD方法。

甜高粱与苜蓿混合不同比例的青贮饲料，甜高粱采自塔里木大学动物科学学院实验站，苜蓿采自第一师五团。甜高粱与苜蓿青贮原料的化学成分见表1。

3 消除边界效应的四中点估计方法

在运用Directly-Mean EMD方法进行本征模态函数分解时, 求出信号的中点曲线是非常关键的一步。而要得到中点曲线首先要确定所有中点的坐标。在许多情况下, 由于信号的起点或终点并不适合当作极值点来处理, 所以信号两端的中点不能如Directly-Mean EMD方法中的步骤2确定。例如: 图2中与第一极大值点B相对应的中点F, 其纵坐标只能通过某种方法给出估计值。类似地, 还有与最后极大值点对应的中点H。以下分别将这两个中点称为“左待估中点F”和“右待估中点H”。利用左右待估中点以及其他中点(图 2中用“o”表示的点)便可拟合出样条曲线, 即中点曲线m1(t)。由于这些中点所跨横坐标区间一般短于原信号横坐标区间,这样得到的中点曲线在信号的两端常常会发生所谓的“飞翼”现象(图1中m1(t)在左、右两端分别发生了过度下行和上翘的现象, 均严重偏离了其平均变化趋势)。鉴于此, 有必要在信号两端再补充两个中点(图2中用“◇”表示), 分别称之为“左延拓中点G”和“右延拓中点J”。以所有中点(用“o”表示的点)以及左、右待估中点, 左、右延拓中点拟合出的样条曲线m1(t)将会完全消除“飞翼”现象(图 2短虚线)。下面讨论左、右待估中点及左、右延拓中点坐标的估计方法, 以便较准确地求取中点曲线m1(t)。

3.1 含有四或四个以上极值点信号的中点曲线求取方法

分四种情况加以讨论: (I)第一极值为极大值, 最后极值为极大值; (II)第一极值为极大值, 最后极值为极小值; (III)第一极值为极小值, 最后极值为极大值; (IV)第一极值为极小值, 最后极值为极小值。首先讨论第一种情况(I), 见图2。

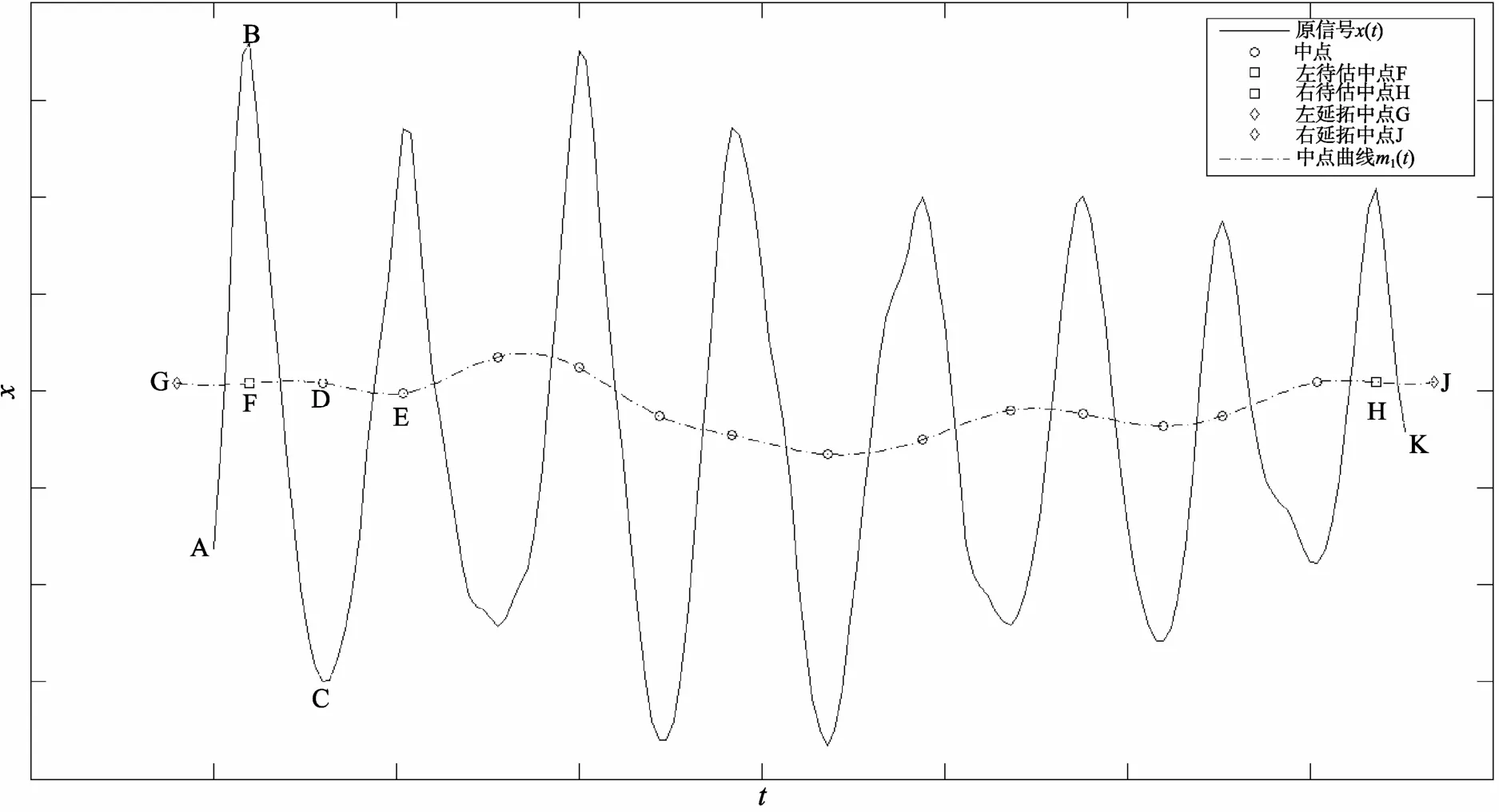
图2 边界处理中几个重要概念Fig. 2 Important concepts in boundary treatment

关于右待估中点H与右延拓中点J坐标的估计方法可仿此进行。

如此, 根据所有中点“o”, 左、右待估中点及左、右延拓中点共同拟合可得到样条曲线。一般地, 这样得到的样条曲线会比原信号长, 将样条曲线介于起点A和终点K之间的部分作为中点曲线m1(t), 此时的m1(t)将会完全消除“飞翼”现象。对于(II)(III)(IV)三种情况, 其估计方法可仿此给出。

3.2 含有三极值点信号的中点曲线求取方法

分两种情况加以讨论: (I)第一极值为极小值; (II)第一极值为极大值。

对于第一种情况(I), 见图 3。首先按(7)(8)和(9)(10)给出左、右待估中点G和H的坐标估计:

然后按(11)(12)和(13)(14)分别给出左、右延拓中点J和K的坐标估计:

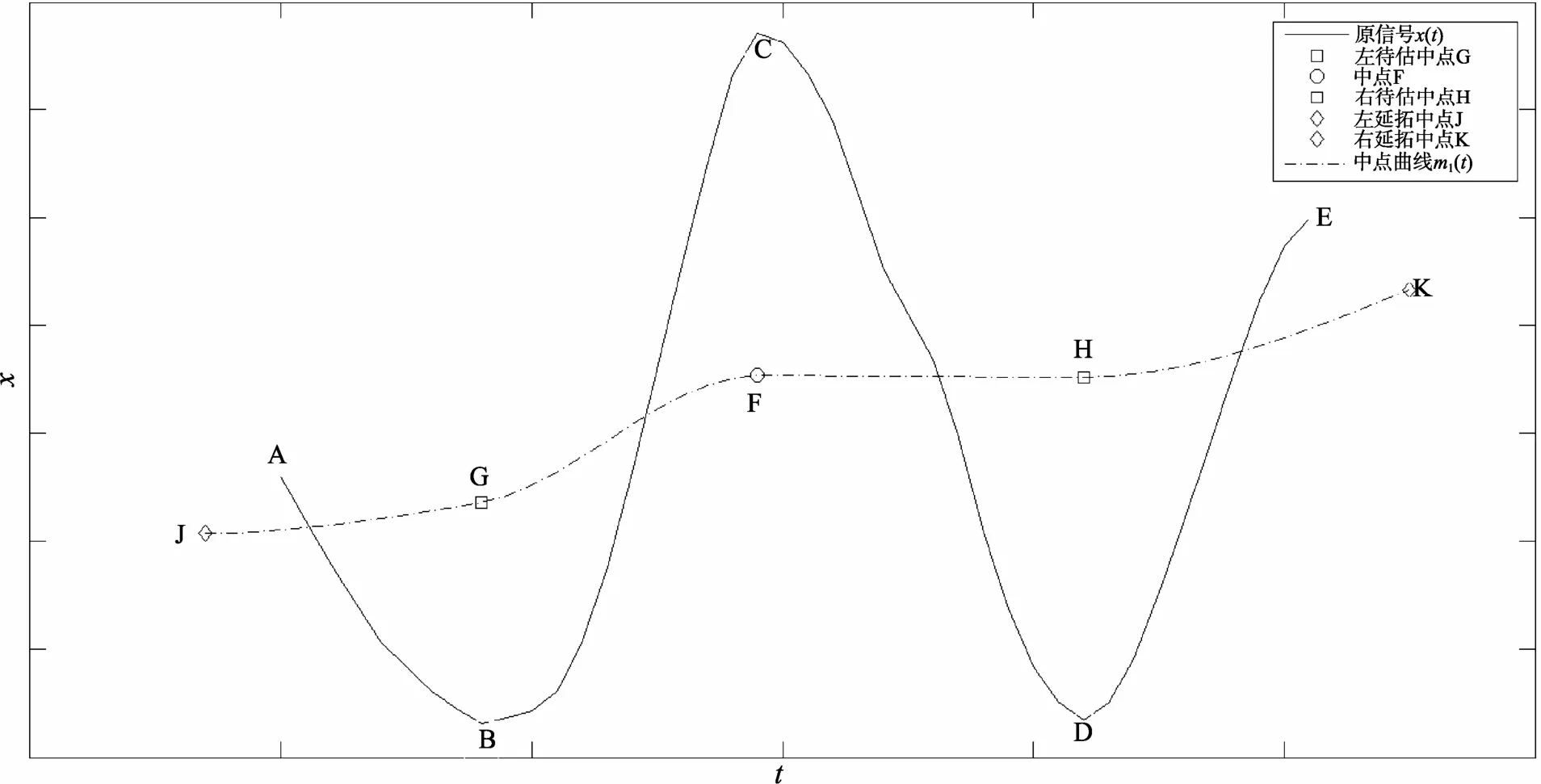
图3 含有三个极值点时求取中点曲线Fig. 3 Midpoint curve calculation in case three extreme points existed

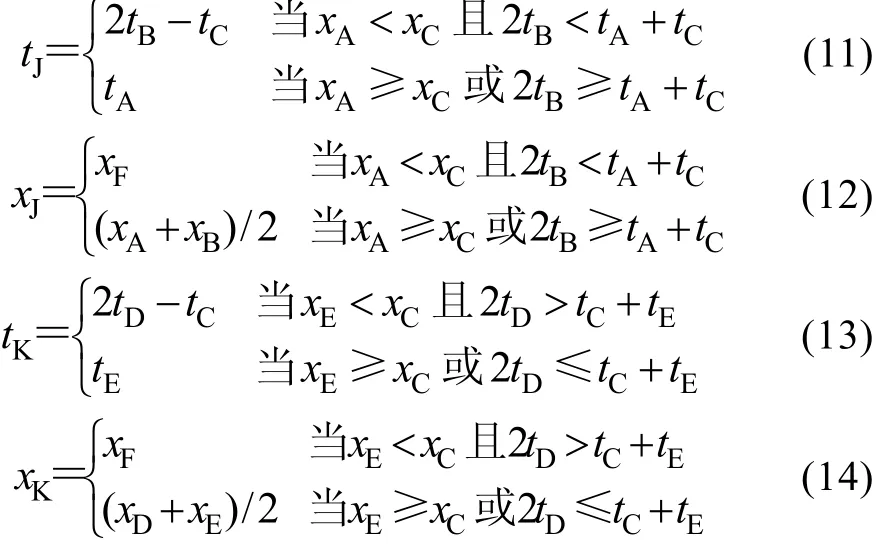
这样利用左、右延拓中点J、K, 左、右待估中点G、H以及中点F五点共同拟合得到样条曲线, 并将样条曲线介于原信号起点和终点的部分作为中点曲线m1(t)。关于第二种情况(II), 可仿此给出。

3.3 含有两极值点信号的中点曲线求取方法

当信号恰有两个极值点时, 也分两种情况加以讨论: (I)第一极值为极小值; (II)第一极值为极大值。对于第一种情况(I), 见图 4。先按(15)(16)和(17)(18)分别给出左、右待估中点E和F的坐标估计:

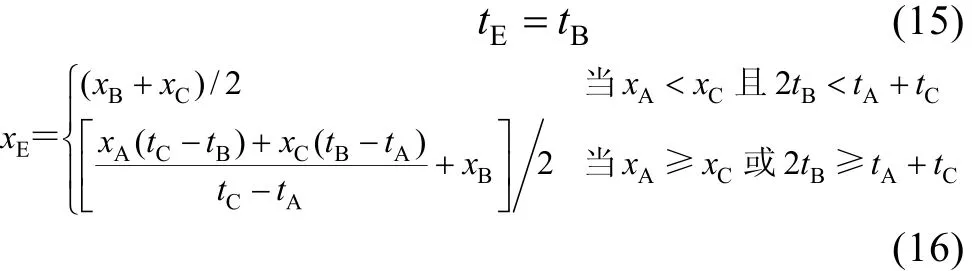
然后, 将过E、F两点且介于起点A和终点D之间的直线段作为中点曲线m1(t)。对于第二种情况(II)可类似规定。

3.4 对于只含有一个极值点或没有极值点的信号, 这时不必求取中点曲线, 可直接将其划归剩余信号

为叙述方便, 将根据上述各种求取中点曲线并按Directly-Mean EMD所述步骤进行本征模态函数分解的过程称为: Directly-Mean EMD四中点估计法。

无论用 Sifting方法, 还是 Directly-Mean EMD方法, 之所以出现“飞翼”现象——边界效应, 其原因就是拟合样条曲线所用型值点两端横坐标区间是原信号横坐标区间的真子集造成的。而根据上述求取中点曲线的过程可以看出, 左右延拓中点所跨横坐标区间是原信号横坐标区间的真子集的情况永远不会发生。因此, Directly-Mean EMD四中点估计法可以完全消除边界效应。

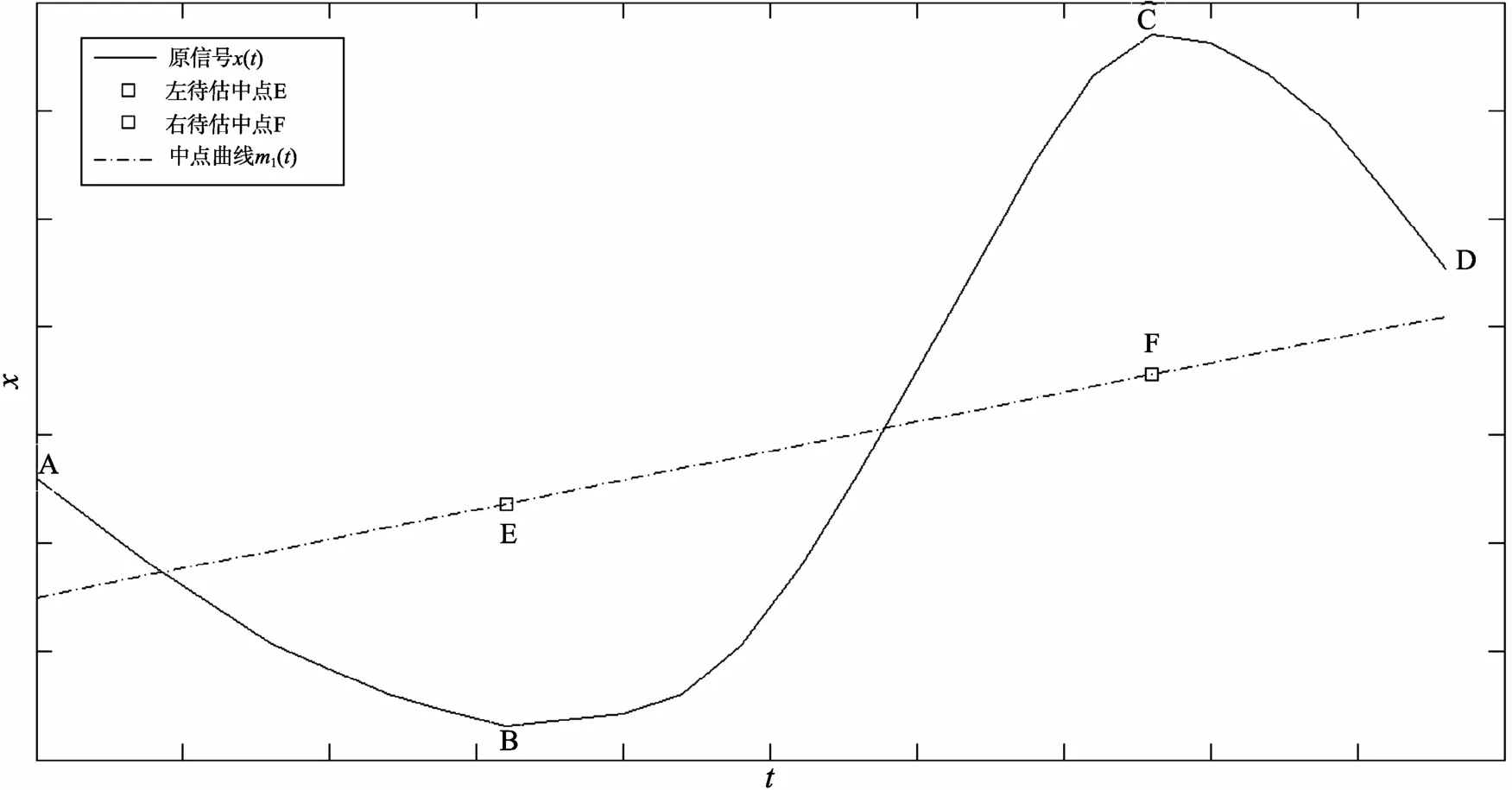
图4 含有两个极值点时求取中点曲线Fig. 4 Midpoint curve calculation in case two extreme points existed

图5 利用Directly-Mean EMD四中点估计法分解日长信号Fig. 5 LOD signal decomposition by using Directly-Mean EMD four-midPoint estimation method

4 用Directly-Mean EMD四中点估计法对日长数据序列进行分解

日长(LOD, length of day)数据序列是综合利用激光卫星(SLR, Satellite Laser Ranging),激光测月(LLR, Lunar Laser Ranging), 长基线干涉术(VLBI, Very-Long-Baseline Interferometry)和全球定位系统(Global Positioning System)等多项先进技术测得的结果。覆盖时间从1962年1月20日到2001年1月6日, 采样间隔为1d, 共包含14 232 d记录(图5(1))。该数据序列的纵轴值代表测得的日长与标准日长(86 400 s)的差(单位ms)。从图上容易看出, 这些年来的日长都比所谓的标准日长要长几个毫秒。将Directly-Mean EMD四中点估计法应用于此数据序列的分解, 共得到 11个本征模态函数(图 5(2)～(12))和一个剩余项(图 5(13))。其中, 第一本征模态函数(图5(2))的平均周期约为13.6 d, 为半个交点月周期。第二本征模态函数(图5(3))的平均周期约为27.55 d,为一个近点月周期。这两模态的物理意义十分明显。第六本征模态函数(图 5(11))较好地反映了其低频变化趋势。其他模态项的物理意义有待进一步研究。从分解结果来看, Directly-Mean EMD四中点估计法不仅从原数据序列中分离出两个具有明显物理意义的本征模态函数, 而且边界效应也处理得很好。

5 结论与讨论

Directly-Mean EMD四中点估计法与 Sifting两种分解方法都是从原信号中减掉平均曲线, 逐渐得到上下包络关于零点对称的本征模态函数。只是求取平均曲线的方法不同。Sifting方法是对极大值点和极小值点分别进行两次样条插值, 并对所得两样条曲线取平均的方法得到平均曲线; 而Directly-Mean EMD四中点估计法方法则通过先求取信号的中点, 再用这些中点直接拟合出中点曲线,即平均曲线。通过实例比较, 两种方法在不考虑边界效应的情况下, 所得平均曲线基本一致。除此之外, Directly-Mean EMD四中点估计法还具有如下优点:

(1)Directly-Mean EMD方法由于只需要一次样条插值计算, 因而减少了计算量, 可以提高分解速度。(2)在进行样条插值时, Directly-Mean EMD四中点估计法参与插值的中点数几乎是Sifting方法参与插值的极大值点数或参与插值的极小值点数的两倍。因而, Directly-Mean EMD四中点估计法可以有效避免因插值节点过于稀疏所产生的不必要大幅度波动。从而使所得中点曲线更加精确。

Directly-Mean EMD 四 中 点估计法 是 对Directly-Mean EMD的进一步完善。与Sifting方法相比不仅具有上述(1)(2)两个优点, 还通过引入左、右待估中点和左右延拓中点及其估计, 完全消除了分解过程的边界效应。同时, 对信号中含有较少极值点的情况进行了讨论, 为Directly- Mean EMD的具体实施制定了统一的处理规则。

[1] Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition method and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proc R Soc, 1998, 454: 903-995.

[2] 黄大吉, 赵进平, 苏纪兰. 希尔伯特-黄变换的端点延拓[J]. 海洋学报, 2003, 25(1): 1-11.

[3] 沈路, 周晓军, 张志刚, 等. Hilbert-Huang变换中的一种端点延拓方法[J]. 振动与冲击, 2009, 28(8): 168-171.

[4] 刘慧婷, 旻张 , 程家兴. 基于多项式拟合算法的 EMD端点问题的处理[J]. 计算机工程与应用, 2004, 16: 84-86.

[5] 胡爱军, 安连锁, 唐贵基, 等. Hilbert-Huang变换端点效应处理新方法[J]. 机械工程学报, 2008, 44(4): 154-158.

[6] 孙华刚, 冯广斌, 曹登庆, 等. 经验模态分解端点波形延拓改进方法研究[J]. 电子测量与仪器学报, 2010, 24(4): 319-326.

[7] 曹冲锋, 杨世锡, 杨将新, 等. 一种抑制EMD端点效应新方法及其在信号特征提取中的应用[J]. 振动工程学报, 2008, 21(6): 588-593.

[8] Zhong Youming, Qin Shuren, Tang Baoping. Research on theoretic evidence and realization of Directly-Mean EMD method[J]. Chinese Journal of mechanical engineering, 2004, 17(3): 399-404.

(本文编辑: 刘珊珊)

Four-midpoint estimation method removing boundary effect of EMD

ZHANG Li-zhen1, LIU Tan-ran1, WEI En-bo2
(1.College of Mathematical Science, Ocean University of China, Qingdao 266100, China; 2. Institute of Oceanology, the Chinese Academy of Sciences, Qingdao 266071, China)

Jan., 13, 2012

intrinsic mode function (IMF); directly-mean EMD method; four-midPoint estimation method; Hilbert-Huang Transform; LOD (length of day)

On the basis of directly-mean EMD method, four-midpoint estimation formula according to all kinds of possible cases at both ends of signal was given by introducing the concepts of left and right undetermined middle points, left and right extended middle points. Four-midpoint estimation method for EMD, which can eliminate boundary effect completely, was established. This new method decompose signal into intrinsic mode functions and eliminate boundary effect more quickly and efficiently. The improvement on decomposition speed was brought by the reduction of the spline interpolation number. And the large fluctuation generated due to too sparse interpolation nodes was avoid, which made decomposition results more accurate. The new method was applied to the mode decomposition of length of day (LOD) data and a satisfactory decomposition result is obtained.

O29; P183.3+1

A

1000-3096(2013)04-0103-08

2012-01-13;

2013-02-04

国家自然科学基金资助项目(40876094)

张立振(1962-), 男, 山东高唐人, 副教授, 博士, 研究方向为数学, 物理海洋学, E-mail: goldfield@ouc.edu.cn