高职经济数学教学改革的新方向——以“模块专业一体化+工具实现”为教学实例

廖仲春

（长沙民政职业技术学院，湖南长沙，410004）

经济数学课作为高职院校文科类专业的一门基础公共课，也是后续专业课的工具课，对学生以后的工作、生活也会产生深刻影响。这就要求经济数学应以专业、工作和生活需求为出发点选择教学内容，为后续的专业课程服务以及为学生以后的工作、生活提供恰到好处的数学支撑。因此，如何在高职经济数学教学中，创新教育模式，改革教育内容，在数学课程中渗透专业思想，强化数学的实际应用，最终实现学生的数学能力与应用能力的综合提高，已成为高职院校经济数学课面临的重要而迫切的任务。

一、高职经济数学课程改革的进程

“模块压缩型”和“举证应用型”是近些年高职经济数学课程改革经历的两个阶段。第一阶段为“模块压缩型”，即将传统的数学内容删除或减少复杂的数学证明和推导等论证过程，其他知识点也尽量删繁就简，压缩成若干知识单元(模块)，以适应不同专业“宽而浅”的发展需要。即便如此，在这个阶段，不管是教学内容还是教学方法，仍没有脱离传统数学的教学模式。第二阶段为“举证应用型”，即基于传统的数学知识的前后逻辑联系，以关键知识点为核心整合相关知识形成若干模块，并在每个模块的后面随即加入数学知识的应用内容，力图突出数学知识的应用，但引进的少许实例实际是附之皮毛、一笔带过，并依然注重数学计算方法与技巧。这样的改革依然存在“教的没有用、用的没有教”，特别是数学知识在专业学习和生活中的应用功能并不突出，教学效果不明显。

本文提出“模块专业一体化+工具实现”的新思路，并以此这作为高职经济数学教学改革第三个阶段的目标，旨在实现数学与专业的融合，促进数学知识模块与专业案例形成一体化模式，同时改革经济数学教学手段，培养学生应用数学软件等工具处理复杂的数学计算的能力，以期充分调动学生的学习积极性，培养学生在专业学习中的数学思维习惯和善于运用工具简化问题的学习习惯，使经济数学更具魅力，教学相长。

二、高职经济数学改革方向——模块专业一体化+工具实现

（一）经济数学的内容与专业相结合

高职经济数学课除了让学生学习与生活或专业有关的数学知识外，更重要的是挖掘其在专业中的应用实例，并运用于教学之中，实现数学与专业及生活实际真正融合，使数学的广泛应用性得以很好的体现。那么怎样做到高职数学教学内容更好地贴近专业和生活实际？笔者通过查找专业核心课程，访谈专业教师，找出与经济数学联系紧密的知识模块：第一模块——生活数学；第二模块——专业数学，其中第一模块介绍工资纳税问题、单利复利、房贷按揭、信用卡的计算等；第二模块介绍边际成本和收益、最优方案、总成本和总收入、最小成本最大收益、生产总值、投入产出模式、概率计算与成果因素分析、经济预测与趋势分析等。

我们尝试形成“以案例驱动为主”的教学模式。该模式可展开为：案例引入——数学知识点——案例运用。以生活中实际发生的事件或专业实践中真切发生过的场景和结果作为“案例引入”环节，通过案例驱动学习相关的数学知识，讲数学知识理解弄懂后再回到生活或专业的案例中去融会贯通，使所学的知识得以应用。所以案例的选择是关键。

例如在讲导数的知识点时，案例引入为:一般情况下，从长沙开往岳阳的长途汽车正常票价均为45元。在汽车即将出发的时候，一位匆匆赶来的乘客要求以30元上车，尽管国营公司的车上尚有空位，还是拒绝了他的要求，而私人公司的售票员却愉快地以30元成交了。纵观其过程与结果，哪家公司的行为更理性呢？

问题分析：45元的运输服务被这名乘客用30元就享受了，乍一看私人公司似乎亏了15元。但如果用边际分析法分析评判，反倒让人觉得私人公司见机行事的确有比国营公司精明的地方。因为这里涉及到边际收益和边际成本这两个概念。在管理专业中产品总量对时间的导数就是总量的变化率，如:产品总收益对产量的导数就是产品收益的变化率（边际收益），产品总成本对产量的导数就是产品成本的变化率（边际成本）等。

案例运用：

销售某商品Q台的收益函数为R(Q)=800Q-Q2/4（元），试求：（1）边际收益函数；

（2）销量为200台时的边际收益。

这种模式应用数学知识解决专业实践中的现实，既强化了学生数学知识与技能的学习，又服务了专业，调动了学生学习数学的热情和积极性，对他们来说更实用、更有价值。

（二）问题解决与数学工具相结合

数学课程的设计与实施应重视运用现代信息技术，特别是让学生学会利用数学软件等工具进行问题的求解。如:微软开发了一款号称超级计算器的软件——微软Math4.0,它包括众多的数学公式与方程，学生们不必纠缠于枯燥的公式记忆，也无须以笔算纸载的方式处理繁琐的计算，只需通过选择即可直接使用，按一定程序即可得出结果，既提高学生们的学习效率，同时也提高了他们学习的乐趣。Math4.0为数学教与学提供了理想的环境，它将重复性、机械性的数学劳动交给计算机去完成，优化了教学过程，强化了学生应用能力的培养。

例如:生产某产品Q件时的总成本函数为：

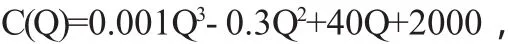
求产量Q分别为50、100、200时的边际成本，并指出它们的经济意义。

解：边际成本函数为

第一步：在工作表中输入

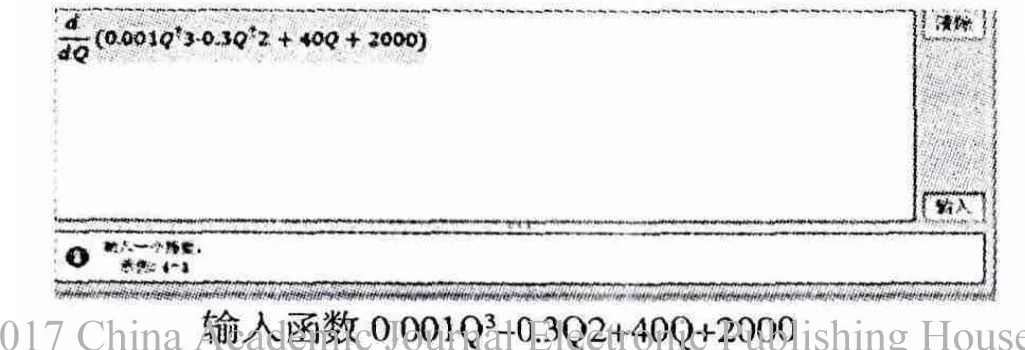
它们的经济意义是:在产量分别为50、100、200的基础上再生产一个单位产品，总成本的增加分别为17.5、10、40。

由于数学软件等工具在教学中使用，学生计算能力得到解放，因此，选择的例题、设计的问题，都是以真实的事例为背景，以原始数据出现，让学生真正体验生活中的数学，提高他们观察生活的能力、分析及解决实际问题的能力。

例：小李买了一套住房，首付一定的金额后，其余20万元采用公积金贷款方式，公积金贷款年利率：4.5%，贷款期限10年，每月底付款一次，有两种还款方式可供小李选择，等额本息和等额本金。小李选择哪种方法能节省利息？

这样的素材对学生来说背景十分熟悉，实用价值又高，现在只需运用按揭房贷计算器的计算功能就能较快地完成这次决策，因此学生们的学习积极性被有效地调动起来了。

等额本息还款法计算：

结语

在近几年的教学实践过程中，通过“模块专业一体化+工具实现”的教学改革，不仅让学生体验了问题解决的过程，更重要的是引导学生用数学的方法思考实际中的问题，运用数学工具解决这类问题，长期坚持，必将引导学生“数学”地生活和工作。

[1]云连英.以应用为主线的高职数学课程改革实践[J].职业技术教育，2009，（17）.

[2]冯天祥.高职院校数学教育的问题与对策[J].教育与职业，2009，（9）.

[3]高瑶，马润宝.高职数学教学中渗透专业学科应用的探讨[J].职业教育,2009,(2).

[4]李鹤.Mathematica软件在高等数学教学中的应用[J].科技创新导报, 2011,(1).