大兴安岭地区森林叶面积指数测定与遥感估算1)

李贺平 肖 克 范文义 温一博 满子源 孙晟昕

(东北林业大学，哈尔滨，150040)

叶面积指数(leaf area index，ⅠL，A)的提出首先开始于作物学。1917年，作物生理作为一门学科由Balls 提出时，主要目的是明确作物产量发展的动态学［1］。20 世纪40年代中期，英国农业生态学家Watson 在英格兰Rothamsted 田间工作基础上提出了叶面积指数的概念并采用ⅠL，A来反映植物叶面的数量变化［2］。Chen［3］1992年正式提出了ⅠL，A定义，即:单位地面面积上总叶面积的一半，并进行了验证，目前已被普遍接受。叶面积指数为植物冠层表面物质、能量交换的描述提供了结构化的定量信息，是估计植物冠层功能的重要参数，也是生态系统中最重要的结构参数之一［4］。随着遥感技术的日益成熟，利用遥感技术大区域估算植被叶面积指数已被广为应用。目前利用遥感的方法估算ⅠL，A主要有统计模型和物理模型两大类。统计模型主要利用植被冠层光谱数据及其变换形式与ⅠL，A建立模型来反演区域植被ⅠL，A，由于不同地区植被类型和土壤背景不同，统计模型存在着随时间和地点而变化的缺陷，但是其参数较少、简单易行且效率较高，故而被广泛使用;物理模型是基于植被—土壤波谱特性及非各向同性辐射传输基础上建立的反演模型，其物理意义明确，但存在模型参数多且不易确定、计算量大、耗时长等不足［5］。国内对大兴安岭地区森林叶面积指数的研究很多，但是由于森林植被的复杂性及实测数据的精度原因，使得森林植被ⅠL，A与从遥感图像上提取的各种植被指数的相关性具有很大的不稳定性。本文以TRAC －Ⅱ实测的41 个样地真实叶面积指数与对应区域遥感影像上提取的植被指数建立统计模型，对区域ⅠL，A进行估算，并从41 个样地中分离出27 个纯针叶树种样地，对纯针叶树种样地真实叶面积指数与植被指数建立模型并估算区域ⅠL，A，对二者的估算精度进行对比研究，为进一步深入研究分树种测定并估算森林叶面积指数提供参考。

1 研究区概况

研究区域位于黑龙江大兴安岭地区塔河林业局境内的盘古林场。盘古林场位于塔河县(东经123°19' ～125°48'，北纬52°9' ～52°23')城西北部96.5 km 处，林场西北与漠河县、开库康乡交界，东南与呼中林业局、塔河镇、瓦拉干镇接壤，施业区面积152 127 hm2，森林覆盖率为88.86%，主要树种为:落叶松(Larix gmelinii)、白桦(Betula platyphylla Suk.)、樟子松(Mongolica litv)、杨树(Populus)等。属于寒温带大陆性季风气候，冬季漫长而寒冷，夏季短暂而湿热，年平均气温－2.4 ℃，年降水量460.3 mm，全年无霜期98 d。

2 研究方法

2.1 数据获取及处理

2.1.1 地面实测数据获取

本次试验采用的光学仪器是TRAC －Ⅱ。通过TRAC 测量集聚指数，能够有效地解决集聚效应的问题，减小有效叶面积指数与现实叶面积指数之间计算的误差［6－7］。

2011年8月6日至8月14日间，根据盘古林场森林分布情况，综合考虑龄组结构、立地质量，并结合地形因素，在盘古林场设定了41 个样地，样地大小均为0. 06 hm2。利用TRAC － II 对样地内植被ⅠL，A进行实测，并用GPS 对样地中心进行坐标定位。测定方法为:手持仪器以0.3 m/s 的速度沿与太阳光线垂直的方向并经过样地中心进行走线，考虑林区状况，为保证数据在相同走线时间下获得，每10 m 一暂停，直至走完整条路线，来回两次，取平均值为ⅠL，A值。为排除草本层对测量结果的影响，仪器高保持在距地面1.2 m 左右。测量时间选择在晴朗阳光充足的上午9:30 至下午15:30 期间。地面实测样地数据分布情况为:纯针叶林样地27 个，ⅠL，A值分布在0.5 到3.36 之间，优势树种为落叶松、云杉、樟子松;纯阔叶林样地9 个，ⅠL，A值分布在0.22 到3.83 之间，优势树种为白桦、赤杨;针阔混交林样地5个，ⅠL，A值分布在1.25 到3.25 之间。

2.1.2 遥感数据处理

本研究采用2011年8月的Landsat TM 遥感影像，轨道号为121/23，图像云量少，基本与地面实测数据同时相。对遥感影像进行几何精校正，纠正误差小于0.5 个像元。对图像进行传感器定标和辐射校正，并对图像进行大气校正。

从校正后的遥感影像中提取植被指数时，根据外业调查过程中使用GPS 记录的样地中心坐标来对应提取相应遥感数据。TM 遥感影像对应的像元面积为0.09 hm2，而外业过程中设定的样地大小为0.06 hm2，由于样地中心未必能够准确地落入遥感影像上相应像元的中心，故研究在提取样地对应植被指数时采用四邻域法，即在样地中心坐标对应的像元及其相邻的正东、正南、正西、正北共5 个像元上提取植被指数，并取平均值，作为该样地对应的植被指数值。

3 种植被指数分别为:

比值植被指数=RN，I/R;

归一化植被指数=(RN，I－R)/(RN，I+R);

差值植被指数=RN，I－R。

式中:RN，I为近红外波段的反射值;R 为红光波段的反射值。

3 种植被指数计算结果见表1。

表1 植被指数

植被指数提取过程中发现编号为2、7、8 的3 个样地位于遥感影像之外，所以直接剔除。

3 ⅠL，A模型拟合

3.1 数据异常点剔除及分析

将实测的ⅠL，A值与3 种植被指数采用两种方法进行分析:全区域分析，即不分树种的所有样地植被的ⅠL，A与植被指数间的相关性分析;纯针叶树种区域分析，即从实测样地中分离出纯针叶林样地，进行样地植被的ⅠL，A与植被指数之间的相关性分析。根据散点图，发现ⅠL，A与各植被指数整体相关性很高，故选择3 种曲线对两种方法下样地植被的ⅠL，A与植被指数进行拟合分析，其表达式分别为:

线性模型，A:Y=b0+b1X;

二次项模型，B:Y=b0+b1X+b2X2;

指数模型，C:Y=b0×eb1X。

将75%的样地数据进行模型拟合，25%留作独立性检验。根据实测ⅠL，A与预测ⅠL，A值之间的残差数据，设定一个剔除异常值的标准化残差阈值Ek，若样本残差Ei＞Ek或Ei＜－Ek时，认为该点为异常点，剔除该点。本试验处理中设定标准化残差阈值为1，在此样本中，将样地编号为25、30、33、41 的点剔除。导致数据异常的原因可能为外业数据测定时的错误，也有可能是利用TRAC－Ⅱ测定数据过程中受外界环境干扰导致仪器失常从而引起数据异常。

3.2 模型的独立正态等方差检验

3.2.1 独立正态性检验

当模型残差呈现非正态分布时，不符合统计模型适用条件，须对残差的正态分布进行检验。文中采用单个样本的K－S 检验，以确定K－S 检验中统计量Z的值。如果相伴概率的值明显大于给定显著水平α=0.05 的值，Z 值越小，则认为样本总体与假定的分布没有显著性差异，即误差项服从正态分布。

由表2、表3两类区域分析中拟合模型的残差正态性检验结果看，相伴概率Sig.值均明显大于给定的显著水平α 的值，可以认为误差项服从正态分布。但相对比较来看:在纯针叶树种区域拟合的模型中，ⅠR，V—ⅠL，A拟合的线性模型、ⅠN，D，V—ⅠL，A拟合的二次项模型及ⅠD，V—ⅠL，A拟合的线性模型及二次项模型显著性稍低;全区域拟合的模型中，ⅠR，V—ⅠL，A拟合的线性模型和指数模型、ⅠN，D，V—ⅠL，A拟合的线性模型显著性稍低。

表2 纯针叶林区域模型残差正态性检验结果

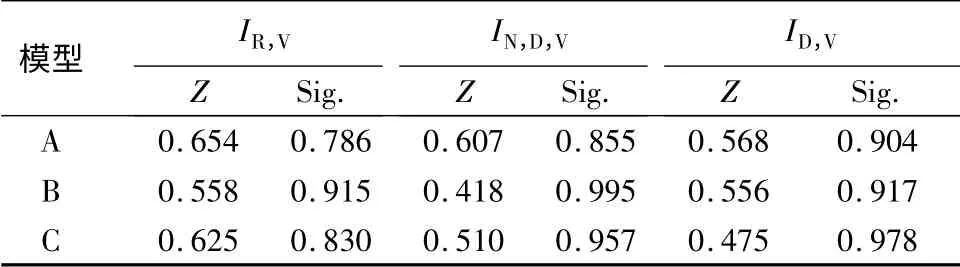
表3 全区域模型残差正态性检验结果

3.2.2 等方差性检验

对于误差项的等方差性检验，在拟合一个模型后，为了考察模型对所有数据的适用性，利用残差分析，对误差项的等方差性进行检验。由于拟合模型较多，本文仅选取代表性较好的等方差检验图，见图1、图2。

图1 纯针叶树种区域拟合模型残差等方差性检验

从纯针叶树种区域3 种植被指数分别拟合的3种模型残差图整体效果来看，点的分布均是随机的，未出现趋势性，认为回归模型拟合适当。

从全区域分析3 种植被指数分别拟合的3 种模型残差图整体效果来看，点的分布也均是随机的，未出现趋势性，认为回归模型拟合适当。

3.3 回归方程的显著性检验

对于拟合模型的显著性检验，分为拟合优度检验和F 检验。R2(相关系数的平方)的大小直接反映了回归方程的显著程度，R2越接近于1，拟合效果越好。Sig.(尾概率)也反映了模型的显著性水平，若Sig.小于显著水平α，则表示模型能够较好地拟合样本数据。但当样本容量的个数与自变量的个数接近时，R2=1，所以F 检验能够更好地反映模型的拟合度。给定一个显著水平α=0.05，当F ＞F(df1，df2)(F 是统计量的值，df1、df2是自由度)时，认为模型是显著的。建立纯针叶树种区域和全区域分析的3 种形式的模型回归方程，显著性检验结果见表4。

图2 全区域拟合模型的等方差性检验

表4 纯针叶树种区域拟合模型回归方程显著性检验结果

在纯针叶树种区域拟合模型回归方程显著性检验结果(表4)中，F(1，15)=4.54，F(2，14)=3.74，F 值远大于F(df1，df2)，认为通过显著水平α=0.05的检验，但从R2看，ⅠL，A与ⅠN，D，V和ⅠR，V拟合的指数回归模型显著性更为理想。

在全区域拟合模型回归方程显著性检验结果(表5)中，R2均大于0.6，认为各模型拟合较好;F(1，24)=4.26，F(2，26)=3.37，各模型F 值均远大于F(df1，df2)，认为各拟合模型均通过了显著性α=0.05 的检验。从R2上看，ⅠL，A—ⅠR，V拟合的二次项模型、ⅠN，D，V—ⅠL，A拟合的指数模型和ⅠD，V—ⅠL，A拟合的二次项模型显著性更为理想。

4 模型精度独立性检验

4.1 拟合模型选取

综合3.2、3.3 的分析，从两类区域分析拟合的模型中分别挑选出3 个较优模型，分别为:纯针叶树种区域:ⅠL，A—ⅠR，V拟合的指数模型A'，ⅠL，A—ⅠN，D，V拟合的指数模型B'，ⅠL，A—ⅠD，V拟合的指数模型C';全区域:ⅠL，A—ⅠR，V拟合的二次项模型A″，ⅠL，A—ⅠN，D，V拟合的指数模型B″，ⅠL，A—ⅠD，V拟合的二次项模型C″。结果见表6和表7。

表6 纯针叶树种区域较优拟合模型

表7 全区域较优拟合模型

比较纯针叶树种区域和全区域的较优拟合模型，纯针叶树种区域拟合模型相关性总体上有显著提高，但是较全区域分析中ⅠD，V的相关系数并未增大，而有减小，分析原因可能是土壤背景的变化所致。ⅠD，V对土壤背景的变化极为敏感，当植被覆盖率过大时，ⅠD，V对植被的反映灵敏度下降［8］。全区域分析中样地平均地面植被覆盖率普遍较纯针叶树种区域分析中植被覆盖率大，可能是导致ⅠD，V的相关系数不增反减的原因。

4.2 模型精度对比分析

鉴于各种植被指数与ⅠL，A间采用不同的回归分析方式，因此不能仅仅依据相关系数的高低比较回归分析精度。为进一步验证各植被指数估算的ⅠL，A精度，需求出各预测方程的相对误差。相对误差越小，表明精度越高［9］。按检验数据占样本总数25%的比例，选择全区域和纯针叶树种区域分别预留的9 块和6 块样地数据作为检测数据，将样本检验数据代入以上A'、B'、C'、A″、B″、C″模型中，求取ⅠL，A预测值，计算平均相对误差(MR，E)、均方差根(RM，S，E)和拟合精度，以对模型进行精度检验。

式中:Z 和Y 分别表示真实值和预测值;i 和n 分别表示检验样本的序号和总数。

计算结果见表8和表9。

表8 纯针叶林区域拟合模型精度检验结果

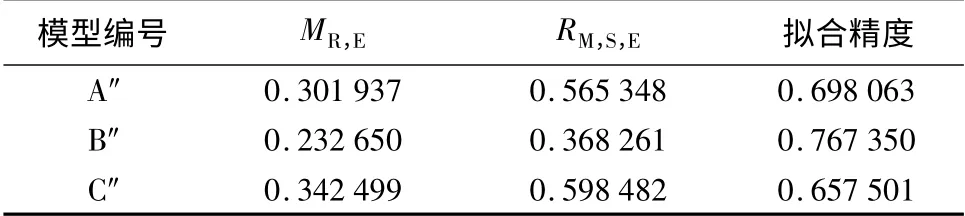
表9 全区域拟合模型精度检验结果

对于纯针叶树种区域，对比分析拟合的3 个较优模型发现，B'模型的R2高达0.821。从代入检验样本后的精度可以看到，B'模型平均相对误差MR，E最小，为21.1362%，而且拟合精度最高，达78.996 3%;B'模型RM，S，E比A'模型低17.910 04%，比C'模型高3.510 29%。综合分析可以认为，纯针叶树种区域估算ⅠL，A的拟合模型中，ⅠL，A—ⅠN，D，V拟合的指数模型相关性最好，显著性最高。纯针叶树种区域ⅠL，A—ⅠN，D，V拟合模型曲线见图3。

本试验全区域利用植被指数估算ⅠL，A的各拟合模型中，相关性最高的B″模型的R2为0.771。由全区域拟合模型精度检验结果(表9)可以看出，B″模型的平均相对误差MR，E和均方差根RM，S，E均为最小，且拟合精度最高，达76.735%，故对于全区域拟合模型中，ⅠL，A—ⅠN，D，V拟合的指数模型为最优模型。

图3 纯针叶树种区域ⅠL，A—ⅠN，D，V拟合模型曲线

5 结论与讨论

对于全区域，利用从TM 遥感影像上提取的植被指数对ⅠL，A进行估算，发现ⅠN，D，V估算ⅠL，A的指数模型相关性最好，R2达到77.1%，精度达到76.733 5%，估算模型为ⅠL，A=0.061 ×exp(4.537 ×ⅠN，D，V);对于纯针叶树种区域，ⅠN，D，V估算ⅠL，A的指数模型ⅠL，A=0.059 ×exp(4.612 ×ⅠN，D，V)为最优模型，其R2为82.1%，模型精度达到78.996 3%。通过不同植被指数建立估算ⅠL，A的模型中发现，ⅠN，D，V拟合的指数模型最适于估算植被ⅠL，A。

由于全区域分析中针、阔叶树种没有进行分类处理，故其森林植被类型比较复杂，从而导致遥感估算植被ⅠL，A过程中不稳定性因素增加。对于分类后的纯针叶树种区域，其植被波谱信息一致性增强，遥感估算植被ⅠL，A的精度有显著性提高。通过纯针叶树种区域ⅠL，A估算模型和全区域ⅠL，A估算模型的相关性及精度对比发现，纯针叶树种区域ⅠL，A估算模型的相关性比全区域ⅠL，A估算模型高5%，模型精度高2.252 8%，所以分树种估算森林叶面积指数能够明显地提高估算精度。

［1］ 王希群，马履一，贾忠奎，等. 叶面积指数的研究和应用进展［J］.生态学杂志，2005，24(5):537 －541.

［2］ de Jesus W C，do vale F C R，Coelho R R，et al. Comparison of two methods for estimating leaf area index on common bean［J］.Agronomy Journal，2001，93(5):989 －991.

［3］ Chen J M，Black T A. Defining leaf area index for non-flat leaves［J］. Plant Cell and Environment，1992，15(4):421 －429.

［4］ 杜春雨，范文义.有效叶面积指数与真实叶面积指数的模型转换［J］.东北林业大学学报，2010，38(7):126 －128.

［5］ 朱高龙，居为民，Chen J M，等.帽儿山地区森林冠层叶面积指数的地面观测与遥感反演［J］. 应用生态学报，2010，21(8):2117 －2124.

［6］ 谭一波，赵仲辉.叶面积指数的主要测定方法［J］.林业调查规划，2008，33(3):45 －48.

［7］ 周宇宇，唐世浩，朱启疆，等.长自山白然保护区叶面积指数测量及结果［J］.资源科学，2003，25(6):38 －42.

［8］ 赵英时. 遥感应用分析原理与方法［M］. 北京:科学出版社，2003:378 －378.

［9］ 徐全芝，张万昌，刘三超，等.黑河流域叶面积指数的遥感反演［J］.干旱区研究，2003，20(4):281 －285.