基于时间序列分析的可燃物含水率预测模型1)

贾鹏超 曲智林 马普龙

(东北林业大学，哈尔滨，150040)

森林火灾发生的重要指标之一是可燃物的含水率，而可燃物的含水率与当地的气象要素如温度、湿度、风速等的相关性较强，是各种气象要素综合作用的结果。Viney［1］等提出了通过建立数学模型来研究在恒定温度下可燃物含水率的变化规律。基于时滞和平衡含水率预测可燃物含水率是目前常用的方法，如Simard［2］模型、Van Wagner［2］模型、Nelson［3］模型、Anderson［4］模型等。金森［5］、曲智林［6－7］等均利用平衡含水率法给出了可燃物含水率的预测模型;但平衡含水率不容易估算，以此分析可燃物的含水率比较困难。本文根据试验地的观测数据，利用时间序列分析理论建立一个可燃物含水率实时变化的预测模型，并根据之前某些时刻的可燃物含水率及气象因子的值预测下一时刻可燃物含水率，从而为森林火灾危险性的预报提供理论依据。

1 研究方法

1.1 数据来源

研究所用数据为2009年3月23日至2009年3月29日黑龙江海林县石河子(北纬43°28' ～45°69'，东经128°3' ～130°47')林场试验地的观测数据。观测木为长20 cm、外直径2.6 cm、内直径为2.1 cm 的内空的椴木。观测木安装在观测仪器上，观测仪器每小时自动收录各项数据。收录的数据包括时间、气温、相对湿度、风速、风向、降水量、观测木的含水率和温度等。

根据试验地的观测数据，统计出各影响因子的取值范围，见表1。风速分为6 级:0 级为0 ～0.2 m/s，1 级为0.3 ～1.5 m/s，2 级为1.6 ～3.3 m/s，3 级为3.4 ～5.4 m/s，4 级为5.5 ～7.9 m/s，5 级为8.0 ～10.7 m/s，6 级为10.8 ～13.8 m/s。

处理数据均使用STATISTICA6.0 软件完成。

表1 各影响因子取值范围

1.2 模型建立

时间序列分析理论的主要模型为ARMA(p，q)，即为

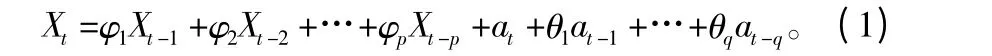
式中:Xt为可燃物在t 时刻的含水率;{at}为白噪声序列;φk、θj均为模型参数;k=1，2，…，p;j=1，2，…，q。

为了研究t 时刻可燃物含水率与之前那些时刻含水率的相关程度，本文利用试验地2009年3月23日至3月27日的观测数据(共120 个样本)以及偏相关系数公式［8］计算可燃物当前时刻含水率与之前各时段含水率的相关性关系，见表2。

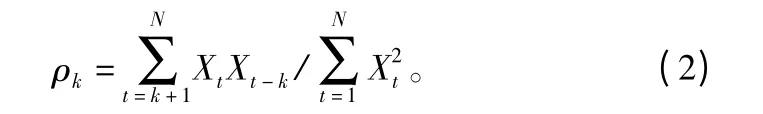
式中:ρk表示某时刻含水率与之前k 时刻的自相关系数;Xt表示t 时刻可燃物含水率。

表2 各时刻可燃物含水率相关性

从表2中可以看出，该观测物的含水率值与之前3 个时刻的含水率相关性较高，说明某一时刻的含水率受前3 个时刻的含水率的影响较大。又由于气象因子随时都在变化，因此本文在时间序列分析的传统模式中引入了干扰因子，即选取模型为:

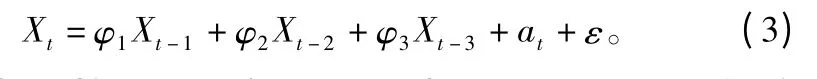
式中:ε 为干扰因子，这里ε 是由bt－1，bt－2，bt－3组合而成;bt－k=θk1Tt－k+θk2Wt－k+θk3Ht－k，k =1，2，3，为t－k 时刻气象干扰因子;φk、θkj均为模型参数，k、j =1，2，3;Tt－k为t －k 时刻空气温度(℃);Wt－k为t －k 时刻风速(级);Ht－k为t－k 时刻空气的相对湿度(%)。

通过此模型可以利用t －1、t －2、t －3 时刻的可燃物含水率值以及3 时刻的气象因子值预测t 时刻的可燃物含水率的值。

2 结果与分析

2.1 基于时间序列分析的可燃物含水率预测模型的建立

为了确定公式(3)中的干扰因子ε 与哪些时刻气象因子相关性较大，本文利用试验地的数据(144个样本)及统计分析理论，将bt－1、bt－2、bt－3不同组合对公式(3)进行回归分析，见表3。

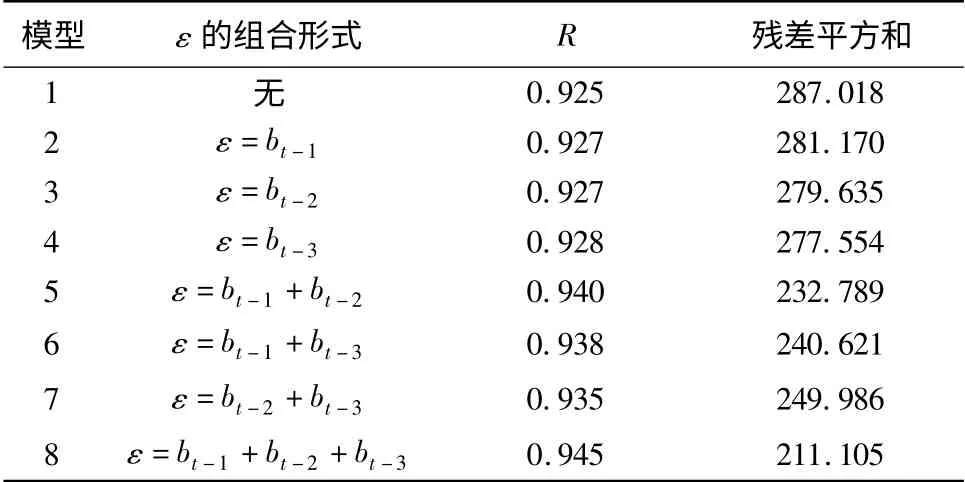
表3 各模型回归分析

从表3中可以得出，通过多元统计回归分析，无论是相关系数R 还是残差平方和的值，模型8 的拟合效果均最好，说明t－1、t－2、t －3 时刻的气象因子对于t 时刻可燃物含水率的变化都有干扰影响。因此本文选取模型8 作为可燃物含水率实时变化的预测模型，即为:

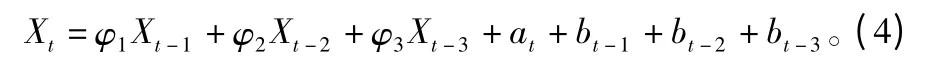
式中:bt－1=θ11Tt－1+θ12Wt－1+θ13Ht－1;bt－2=θ21Tt－2+θ22Wt－2+θ23Ht－2;bt－3=θ31Tt－3+θ32Wt－3+θ33Ht－3。

通过回归分析理论，利用144 个样本对选定模型8 即公式(4)中的参数进行了估计，见表4。

表4 模型中各参数的估计值

2.2 模型检验

利用模型8(公式(4))对试验地2009年3月28日的各时刻可燃物的含水率进行了预测，见表5。并对模型进行了检验。检验结果表明:当相对误差不超过5%时准确率达95.8%;当相对误差不超过3%时，准确率达91.7%。说明本文给出的模型可以用于预测可燃物的含水率变化。

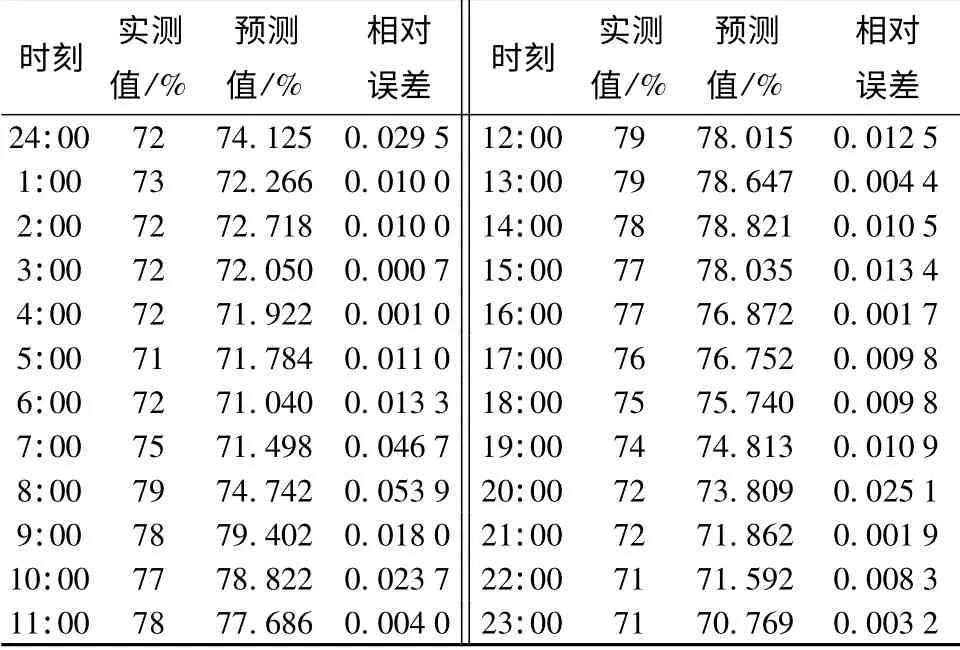
表5 试验地2009年3月28日可燃物含水率实测值与预测值

3 结论

利用时间序列分析理论建立的可燃物含水率变化预测模型，经检验，当相对误差不超过3%时准确率达91.7%，说明该模型可用于预测多时无雨条件下可燃物含水率的变化。利用时间序列分析方法研究可燃物含水率变化，有效地避开了平衡含水率法对可燃物含水率的观测与估算的困难，从检验的结果上看，效果大致相同。本文使用时间序列分析方法研究可燃物含水率变化规律，建模时引入了干扰因子，有效地提高了预测的准确性。

［1］ Viney N R，Catchpole E A. Estimating fuel moisture response time from field observations［J］. Ⅰnternational Journal of Wildland Fire，1991，1(4):211 －214.

［2］ 刘曦，金森.平衡含水率法预测可燃物含水率的研究进展［J］.林业科学，2007，43(12):126 －133.

［3］ Nelson R M，Jr. Prediction of diurnal change in 10 －h fuel stick moisture content［J］. Canadian Journal of Forest Research，2000，30(7):1071 －1087.

［4］ Anderson H E. Moisture diffusivity and response time in fine forest fuels［J］. Canadian Journal of Forest Research，1990，20(3):315－325.

［5］ 金森，李亮.时滞和平衡含水率直接估计法的有效性分析［J］.林业科学，2010，46(2):96 －102.

［6］ 曲智林，李昱烨，闵盈盈.可燃物含水率实时变化的预测模型［J］.东北林业大学学报，2010，38(6):66 －67.

［7］ 曲智林，吴娟，闵盈盈. 具有时滞的可燃物含水率预测模型［J］.东北林业大学学报，2012，40(3):120 －122.

［8］ 王振龙.时间序列分析［M］.北京:中国统计出版社，2003.