三线阵相机体系定向模型研究

余俊鹏 高卫军 孙世君 栗帅

（北京空间机电研究所，北京 1 00076）

1 引言

自20世纪80年代起，三线阵CCD相机技术经过理论研究、工程试验和实践应用，逐渐成为一种重要的空间信息获取手段。1993年，德国以航天飞机为平台进行了三线阵CCD相机的首次空间对地观测试验（MOMS-02/D2），取得初步成果；1996年，德国再次利用俄罗斯MIR空间站搭载三线阵CCD相机进行摄影测量试验（MOMS-2P/PRIRODA）。在这两次试验中，德国宇航中心（DLR）等研究机构完成了三线阵CCD相机影像从辐射处理到空间信息提取的全摄影测量流程[1]，验证了三线阵相机摄影测量技术的可行性。2004年，欧空局实施的的火星快车任务(Mars Express)中，利用高分辨率立体相机HRSC获取大量的火星立体观测影像和加密点数据，在建立火星参考坐标系过程中发挥了重要作用[2]，成为三线阵相机技术应用于外星探测领域的范例。2006年，日本研制并发射了先进陆地观测卫星ALOS，其装载的三线阵立体测绘相机PRISM地面分辨率2.5m，立体覆盖宽度35km，用以绘制全球1∶2.5万比例尺地图。2012年，中国的“资源三号”测绘卫星01星成功发射，其正视全色谱段CCD相机地面分辨率达2.1m，立体覆盖宽度超过50km，具有强大的地理三维数据采集能力，达到目前同类型相机的先进水平[3]。

随着三线阵相机技术的快速发展，人们对于三线阵影像数据的摄影测量方法研究也在不断深入，力求充分发挥三线阵相机技术在对地测绘定位方面的优势。基于这一出发点，本文提出在摄影测量中将三线阵相机整体视作一个刚体运动体系，通过引入三线阵相机投影中心及姿态角之间的几何关系，以一种新的形式表示三线阵相机在成像过程中的空间方位。在此基础上，进一步研究了基于光束法平差原理的三线阵相机体系定向模型。经过仿真试验表明，该定向模型能明显提高三线阵相机的摄影测量精度，不失为三线阵影像几何处理的一种可选参考模型。

2 三线阵相机体系的建立

三线阵相机分为单镜头三线阵相机和三镜头三线阵相机两种类型[4]。单镜头三线阵相机是利用同一镜头的不同视场分别放置前视、正视和后视探测器件，该类型相机一受制于镜头的边缘分辨率，前后视影像分辨率低于正视影像；二受制于镜头视场范围，前后视立体交会角度有限。单镜头主要适用于航空摄影，本文不对该类型相机展开讨论。

三镜头三线阵相机各自具备完整的光学成像系统，可分别独立成像[5]。尽管结构形式上较为复杂，然而各相机光学设计性能可大幅提高，前后视相机光轴夹角可按所需基高比设定，目前主要的光学测绘卫星如“资源三号”即采用这一相机类型。因此，本文以三镜头三线阵相机为研究对象，文中所述三线阵相机特指这一类型。

三线阵相机可看作是由3台线阵相机通过外部约束固连形成的一个内部几何关系稳定的体系[6]，如图1所示。

图1 三线阵相机结构示意图Fig.1 Configuration of three-linear-array camera

为描述三线阵相机体系的空间方位，先将每台相机视作刚体，分别建立其本体坐标系，其中坐标系原点为相机投影中心，XY平面平行于相机像平面，X轴垂直于线阵方向，Y轴平行于线阵方向。相机方位参数包括本体坐标系原点的空间三维坐标(XS，YS，ZS)以及本体坐标系相对于物方空间坐标系的3个欧拉角（，，），即摄影测量中定义的6个外方位元素。三线阵相机体系中正视、前视、后视相机的本体坐标系分别为（OB-XBYBZB）、（OA-XAYAZA）、（OC-XCYCZC），整个三线阵相机体系的空间方位需要用 3 台相机的外方位元素（XSB，YSB，ZSB，B，ωB，κB）、（XSA，YSA，ZSA，A，ωA，κA）、（XSC，YSC，ZSC，C，ωC，κC）共 1 8个参数表示。

上述形式可表达3台线阵相机各自的空间方位，具有普遍的适用性，但未反映出三线阵相机作为一个体系固有的内部关联。为克服这一不足，根据三线阵相机的结构设计特点，引入三线阵相机体系的另一种表达形式。图2为三线阵相机几何关联示意图，将正视相机视作三线阵相机体系的基准参考相机，可以建立前视相机本体坐标系与基准相机本体坐标系的几何关联，图中A-XPYPZP为物方空间坐标系，OB-XB′YB′ZB′为像方空间辅助坐标系，其坐标轴与A-XPYPZP相互平行。

图2 三线阵相机几何关联示意图Fig.2 Geometry of three-linear-array camera

由于两台相机投影中心OA与OB不可能重合，它们之间存在着空间偏移向量，即

式中RB=RBRBRB，为基准相机外方位角元素构成的方向余弦矩阵，表示像方空间辅助坐标系依次旋转B，B，B3个角度后与基准相机本体坐标系平行。

另一方面，假定前视相机本体坐标系依次旋转I，I，I3个角度后与基准相机本体坐标系平行，有

式中RA=RARARA，为前视相机外方位角元素（A，A，A） 构 成的方向余弦矩阵；RAB=RIRIRI为前视相机本体坐标系与基准相机本体坐标系之间的相对旋转矩阵。

公式(1)、(2)给出了前视相机与基准相机外方位元素之间的相对关系。同理，可以得到后视相机与基准相机外方位元素之间的数学关系如下。

CCCC视相机外方位角元素（C，C，C） 构 成的方向余弦矩阵；为后视相机本体坐标系与基准相机本体坐标系之间的相对旋转矩阵。

由上可知，利用基准相机的外方位元素以及前、后视相机相对于基准相机的空间偏移量和相对旋转角共18个定向参 数(XSB，YSB，ZSB，B，B，B，uA，vA，wA，I，I，I，uC，vC，wC，J，J，J )，同样可以完整地描述三线阵相机体系的空间方位。其中uA，vA，wA，I，I，I，uC，vC，wC，J，J，J在三线阵相机立体观成像过程中视作常量，实质上反映了相机之间的几何关联。下面可以看到，以这一表达形式描述三线阵相机的动态成像几何具有独特的优点。

3 三线阵相机体系的定向方法

3.1 线阵相机的成像几何

线阵CCD相机是在相机镜头焦面垂直于飞行方向上放置线阵CCD探测器件，平台向前飞行时逐行推扫获取地面辐射信息，得到连续的条带影像。对于线阵影像，每一扫描行仍满足中心投影，用共线方程表示如下[7]：

式中 (x,y) 为目标的像空间坐标；(x0,y0)为 像主点偏移，理想情况下等于零；f为相机镜头主距；(XS,YS,ZS)为目标像点所在扫描行的外方位线元素；aj,bj,cj(j=1,2,3)为扫描行的外方位角元素 (ϕ,ω,κ)构成的旋转矩阵方向余弦值；()为目标的物方空间坐标。

3.2 线阵相机的影像定向原理

在摄影测量中，影像定向主要通过地面点与像点之间的对应关系来恢复相机成像时的方位信息。由公式(5)可知，线阵相机属于动态摄影方式，影像上每一扫描行对应不同的外方位元素，而一景影像行数通常在10 000以上，包括6×10 000个以上外方位元素。若将如此大量的外方位元素全部作为未知数进行平差求解，在数学上几乎无法实现。为此，德国DLR的学者在三线阵相机技术论证过程中提出了定向片处理方法并用于MOMS-02/D2和MOMS-2P/PRIRODA影像的定向计算，随后被推广应用于其它星载线阵相机乃至机载三线阵相机的数据几何处理，成为线阵相机摄影测量处理的一种常用方法[8]。以下简要介绍其原理。

由于线阵相机成像过程中外方位元素平稳变化，可在影像上按一定时间间隔抽取若干扫描行，称之为定向片。任意扫描行的外方位元素通过与之最邻近的n张定向片外方位元素…，n）内插得到，如式（6）所示：

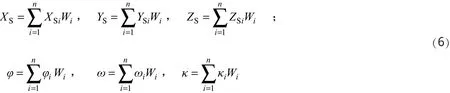
在线阵影像的定向过程中，将各定向片的外方位元素和地面加密点的物方坐标作为未知数。根据光束法平差原理，对公式(5)进行线性化得到如下形式的像点坐标误差方程。

式中x=[XYZ为像点对应的地面点物方三维坐标增量；为各定向片外方位线元素的增量；为各定向片外方位角元素的增量；B为像点坐标（x,y）对(XT,YT,ZT)的偏导系数矩阵；A1为像点坐标对各定向片外方位线元素的偏导系数矩阵；A2为像点坐标对各定向片外方位角元素的偏导系数矩阵；V=为像点坐标观测值改正数向量；L为量测的像点坐标观测值与像点坐标估计值（按外方位元素估计值从物方坐标反算得到的像方坐标）之差；E为单位矩阵，表明此时各像点坐标观测精度相等且观测值权=1。

3.3 三线阵相机体系的定向模型

节2给出了两种三线阵相机体系的空间方位表达形式，与之相应，三线阵相机影像定向可以采用两种方案。方案一是将前视、正视、后视相机各自独立看待，分别设置n1张定向片。每张定向片对应一组6个外方位元素，总的定向未知数个数为N1=3n1?6。方案二是将正视相机作为三线阵相机体系的基准相机，对基准相机设置n2张定向片(n2≤3n1)，前后视相机的外方位元素由其相对于基准相机的空间偏移量和相对旋转角替代，总的定向未知数个数为N2=n2?6+12。在三线阵相机进行多基线摄影测量的情况下，一般有N2

在方案一中，对各台相机的像点观测值均按式(7)列出误差方程。

在方案二中，对基准相机即正视相机上所成的像点，仍按式(7)列出误差方程；对前（后）视相机上所成的像点，按式(8)列出误差方程。

公式(8)与公式(7)的区别在于增加了对相机几何关联参数t的偏导系数。

对于前视相机，t=[uvw为前视相机相对于基准相机的投影中心空间偏移量增量为前视相机本体相对于基准相机本体的相对旋转角增量；

为像点坐标对的偏导系数矩阵；

为像点坐标对的偏导系数矩阵；除像点观测误差方程外，定向模型中还包括地面控制点坐标误差方程和定向参数虚拟误差方程。地面控制点在平差中起空间基准的作用，其坐标误差方程形式为：

式中为控制点物方坐标观测值残差向量，可当作零向量处理；为控制点坐标观测值权矩阵。

引入定向参数虚拟误差方程可以提高解算的精度与稳定性，其形式为：

列出所有误差方程后，按最小二乘平差原理构建法方程系数阵，解出未知数的增量并对其初值进行改正。如此经若干次迭代修正，便可得到三线阵相机定向未知数和地面点坐标的平差值。

利用平差后获得的未知数协方差矩阵，可以从理论上估计影像定向后所能取得的摄影测量精度。若在三线阵影像覆盖区域中提取m个加密点，所有加密点的坐标未知数平均平面理论精度和平均高程理论精度分别为

4 仿真试验及其结果分析

依照上述三线阵相机体系定向模型，笔者编制了相应的仿真计算程序并根据如表1所示的仿真参数进行试验，进而分析两种定向方案下三线阵相机的摄影测量精度。

表1 三线阵相机仿真几何参数Tab.1 Simulation parameters of three-linear-array camera

经模拟得到160个地面加密点，将定向模型中控制点坐标观测值权设为106，定向参数虚拟观测值权设为10-3，由两种方案得到的理论定位精度结果如表2所示：

表2 三线阵相机理论定位精度Tab.2 Theoretical location accuracy of three-linear-array camera

从表2可知，方案一的平面和高程定位中误差分别为0.88m和1.17m，在1个像元地面分辨率左右；方案二中，平面中误差达到0.75m，减小了14.8%，高程中误差达到0.94m，减小了19.7%，平面和高程定位中误差均小于1个像元的地面分辨率。两种定向方案的最大平面误差不超过两个像元，达到了像元级的摄影测量精度，表明本文定向模型及其计算过程是正确的。

与方案一相比，方案二在同等地面控制条件下取得了更高的定位精度。究其原因，方案二所引入的相机几何关联，实际上加强了三线阵影像观测值之间的约束，在平差中可以起到改善法方程组状态、提高求解精度的作用，最终使三线阵影像的对地定位精度得到提高。

5 结束语

本文的主要创新是将三线阵相机视作一个体系，针对其摄影测量应用提出一种新的三线阵相机定向模型。通过仿真计算试验，表明该模型可以有效提高三线阵相机的对地定位精度，为三线阵影像的几何处理提供新的方法。随着后续更多搭载三线阵相机的测绘卫星发射运行，对地观测的时间、空间分辨率将不断提高，本文模型可望在三线阵影像高精度空间信息提取方面得到进一步应用。需要注意的是，模型的应用以相机体系内部的几何稳定性为基本前提。为此，相机研制单位应明确相关设计指标并在测试过程中予以严格的验证，使三线阵相机的摄影测量效能得以充分展现。

（References）

[1] EBNERH,KORNUSW,OHLHOFT,et al.orientation of MOMS-02/D2 and MOMS-2P/PRIRODA Imagery[J].ISPRSof Journal of Photogrammetry&Remote Sensing,1999(54):332-341.

[2] SCHMIDT R,SPIEGEL M,HEIPKEC,et al.Orientation Determination of Tie Points and Bundle Adjustment of HRSCImagesof the Mars Express Mission[J].The International Archives of the Photogrammetry Remote Sensing and Spatial Information Science,Beijing,2008.

[3] 唐新明，张过，祝小勇，等.资源三号测绘卫星三线阵成像几何模型构建与精度初步验证[J].测绘学报,2012,41(2):191-198.TANG Xinming,ZHANG Guo,ZHU Xiaoyong,et al.Triple Linear-array Imaging Geometry Model of Ziyuan-3 Surveying Satellite and Its Validation[J].Acta Geodaetica et Cartographica Sinica,2012,41(2):191-198.(in Chinese)

[4] 王任享.三线阵CCD影像卫星摄影测量原理[M].北京：测绘出版社,2006.WANG Renxing.Satellite Photogrammetry Principle for Three-Line-Array CCD Imagery[M].Beijing:Surveying and Mapping Press,2006.(in Chinese)

[5] 余俊鹏，孙世君.测绘相机内方位元素在对地定位中的误差传播[J].航天返回与遥感,2010,31(2):16-22.YU Junpeng，SUN Shijun.Error Propagation of Interior Orientation Elements of Surveying Camera in Ground Positioning[J].Spacecraft Recovery Remote Sensing,2010,31(2):16-22.(in Chinese)

[6] 高卫军，孙立，王长杰，等.“资源三号”高分辨率立体测绘卫星三线阵相机设计与验证[J].航天返回与遥感,2012,33(3):25-34.GAO Weijun,SUN Li,WANG Changjie,et al.Design and Verification of Three-line Array Camera for ZY-3 High Resolution Stereo Mapping Satellite[J].Spacecraft Recovery Remote Sensing,2012,33(3):25-34.(in Chinese)

[7] WANG Zhizhuo.Principle of Photogrammetry(with Remote Sensing)[M].Wuhan:Press of Wuhan Technical University of Surveying and Mapping,1990.

[8] POLI D.Orientation of Satellite and Airborne Imagery from Multi-line Pushbroom Sensors with a Rigorous Sensor Model[J].International Archivesof Photogrammetry and Remote Sensing,Istanbul,Turkey,2004.

[9] 袁修孝.GPS辅助空中三角测量原理及应用[M].北京：测绘出版社，2001.YUAN Xiuxiao.Principle and Application of GPS-Supported Aerial Triangulation[M].Beijing:Surveying and Mapping Press,2001.(in Chinese)