基于ALE方法的开缝降落伞充气过程研究
高兴龙 高庆玉 张青斌 唐乾刚
(国防科技大学航天科学与工程学院,长沙 410073)
1 引言
降落伞空投过程可分为自由坠落、拉直、充气、稳定下降、着陆几个阶段[1],其中充气过程的力学行为最为复杂,涉及到柔性织物的弹性变形与气动力的耦合作用,是典型的流固耦合问题。该问题的研究一直是航空航天领域的前沿性课题。由于伞衣结构的透气性和大变形等力学特性,使得作用于伞衣表面的气动力分布较为复杂,内外流场呈现极度不规则性,依靠传统的经验理论方法难以对伞衣和周围流场的动力学行为进行准确的预测。
近年来,伴随着计算机技术和计算力学方法的发展,数值模拟技术在降落伞研究领域得到了广泛的应用。俄罗斯早在20世纪70年代就将数值模拟技术引入到降落伞研究领域。美国的T.Tezduyar教授及其领导的“先进流体仿真建模团队”[2-4]基于“变空间域/稳定时间-空间”(Deforming-Spatial-Domain/Stabilized Space-Time,DSD/SST)格式对十字型伞、密实织物伞的流固耦合计算问题进行了深入研究,并开发了针对伞衣结构几何透气性的均质建模方法。法国的政府国防采购部门的Christine Espinosa等人曾利用任意拉格朗日-欧拉(Arbitrary Lagrange-Euler,ALE)有限元方法开发了SINAP软件对降落伞流固耦合现象进行了数值仿真,并基于有限元软件LS-DYNA对降落伞空投试验进行了数值模拟[5]。
相比之下,国内研究者早期对降落伞充气过程的机理研究较多[6-8],近年来则逐渐侧重于对降落伞的动力学计算仿真及工程技术验证,文献[9-11]基于LS-DYNA软件和ALE方法对降落伞开伞过程进行了三维数值仿真。整体来说国内降落伞领域的研究水平近年来得到了显著提高,但研究伞型对象较单一,伞衣结构简单,缺乏对复杂结构降落伞充气过程的三维可视化建模及仿真技术的研究。
本文紧跟国际前沿,基于ALE有限元方法对开缝救生伞进行了充气过程的流固耦合问题研究,数值模拟了降落伞的充气过程,对比分析了开缝救生伞的伞衣变形、开伞动载问题,同时给出伞衣结构在变化流场作用下的三维动态响应及伞衣周围流场的衍变特性,仿真结果符合降落伞充气规律,验证了本方法的有效性。
2 耦合动力学模型
本文主要基于ALE描述下的有限元方法建立降落伞结构和周围流场的动力学计算模型,考虑降落伞开伞过程的复杂物理特性,所采用的计算模型做如下假设:
1)开始充气前伞衣织物处于轴对称的折叠状态,且预应力为0;
2)开伞过程为无限质量情况,忽略重力影响;
3)伞衣流体域入口进气速度不变;
4)低速流动,流体为不可压流;
5)流场为来流速度恒定的准定常流场。
2.1 结构动力学模型
伞衣织物是柔性大变形体,具有典型的非线性动力学特性,且为多孔渗透性介质的薄膜结构。令为空间结构域,固体边界由 ∂表示,可以写出结构的控制方程为:
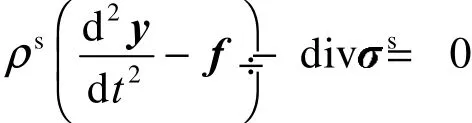
式中 y 是位移矢量;ρs为结构材料密度;f 是作用在结构上的体积力;s为结构体Cauchy应力张量;t为积分时间。
2.2 流场动力学模型
空投过程降落伞开伞速度一般相对较小,可以认为充气过程流体为不可压流。在ALE描述下,有限元网格可以在空间域任意移动,则在参考坐标系下不可压缩流体的N-S方程可写为:
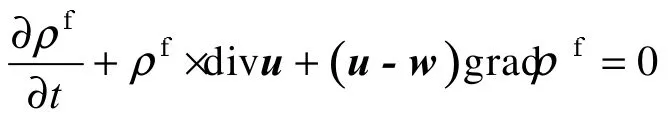
式中 u为流体速度;w 为参考构型下网格点的移动速度;ρf为流体密度。
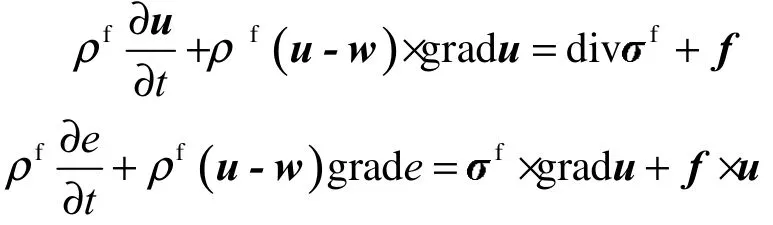
式中 e为物质内能。
显然,ALE描述是包含了欧拉描述和拉格朗日描述的[12]。
对于牛顿流体,应力张量f定义为:
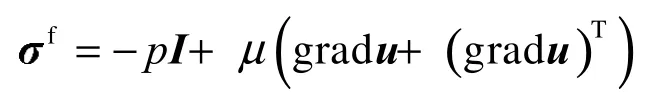
式中p为压力;I为二阶单位张量;µ为动力粘性系数。
在确定控制方程后还需要给定边界条件,Dirichlet和Neumann边界条件为:
2.3 耦合信息传递
在降落伞的整个充气过程的耦合计算过程中,关键是耦合界面信息的传递,本文基于欧拉-拉格朗日描述下的罚函数法[13]进行流体与伞衣结构间节点力信息的传递,该方法允许非匹配的流体和结构网格。
假设流体为渗透性介质,采用显式动力学积分方法,当积分时间t=tn(n为积分时间步)时,结构节点的穿透深度为dn,则下一时刻迭代的结果为:
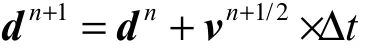
式中v为节点速度矢量;Δt为积分时间步长。
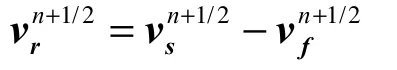
式中vr为主从节点的相对速度;从节点速度即结构节点速度为vs,主节点速度可看作流体单元节点在等参坐标变化所得的某一流体质点速度vf。
3 仿真模型
3.1 开缝伞模型
本文所研究的开缝型救生伞伞衣平面为圆形,整个伞衣被沿辐射方向对称分布的8条缝分成8个扇形伞衣幅,共28根伞绳。缝隙从距伞衣中心一定距离开始,其中4条纵向贯穿缝开至伞衣底边,另4条纵向非贯穿缝开到离底边一定距离。伞顶开有排气孔,伞衣平面几何模型如图1所示,图中 ,分别为伞顶孔直径和伞衣结构直径。
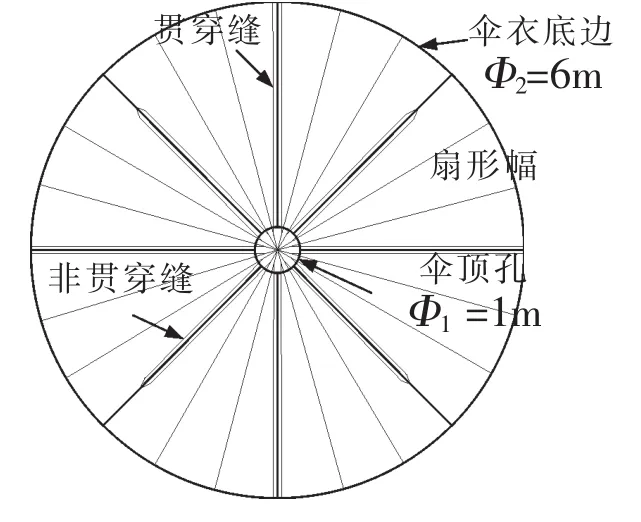
图1 开缝型伞衣结构平面示意图Fig.1 Canopy structure of slots-parachute
降落伞伞衣初始模型的好坏将直接影响到数值模拟的可靠性和精确性,因此需要准确的复制出降落伞初始创建时的几何外形。考虑到柔性折叠织物建模的复杂性,本文暂不考虑织物经向折叠,仅考虑纬向折叠,即只考虑伞系统拉直后充气阶段的仿真计算模型,图2(a)为伞衣初始折叠模型。在建立伞衣初始折叠模型时,需要考虑伞缝的布置,这里在几何建模过程中,在开缝区域用ANSYS软件中常用的“生死单元”进行填充,当作用于伞衣表面的气动力达到所设置的阈值时,则开缝区域单元被“杀死”,即将其刚度矩阵乘以一个很小的因子,死单元载荷为0,气流便可通过开缝区域。图2(b)为伞衣充满时伞缝的张开情况。
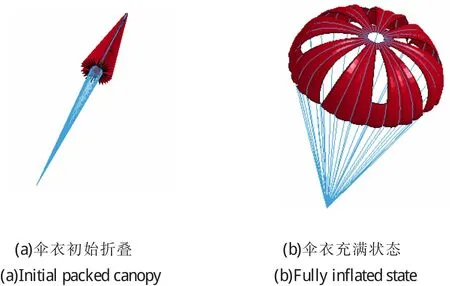
图2 开缝型降落伞3D仿真模型Fig.2 3D simulation model of slots-parachute
3.2 流场模型
为避免壁面反射应力波对计算结果造成影响,应对照降落伞的尺寸和位置适当加大流场尺寸,同时在流出截面设置无反射边界条件。本文所建立的流场模型尺寸为30m×30m×80m。同时为了节省计算资源,并避免伞衣结构对流体的扰动影响,可采用渐变网格划分流场,即对靠近伞衣结构的流体网格进行局部细化,以获得较精确的计算结果。流场网格的截面图如图3所示。
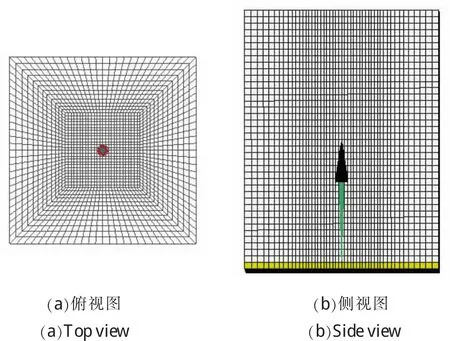
图3 流场网格模型Fig.3 Fluid mesh
4 计算结果
基于所建立的仿真模型,数值计算得到伞衣外形变化、充气时间、开伞动载及流场衍变等结果,本文针对低速空投过程的开伞过程进行研究,来流速度取40 m/s,大气密度为1.18kg/m3。自开始充气至伞衣首次完全充满时间内,根据伞衣外形变化程度,任意选取其中的6个时间点,得到伞衣充气过程外形的三维结构动力学响应结果如图4所示。

图4 伞衣充气过程三维变形图Fig.4 3D change of canopy inflation
充气过程中,伞衣的形状和有效透气性发生改变,伞衣投影面积变化如图5,伞衣最大投影面积为41.2m2。与文献[14]的无限质量情况下伞衣直径和开伞力随时间变化曲线相比,本文所计算获得的开缝伞伞衣外形变化结果基本符合一般降落伞充气过程的变形规律。从充气过程伞衣投影面积的变化可看出,在气流流入时出现较明显的弹性现象,当伞衣首次充满后(即达到最大投影面积时),伞衣充气便达到了稳定状态,并无明显的呼吸现象,这主要是由于开缝伞衣的几何排气特性所致。
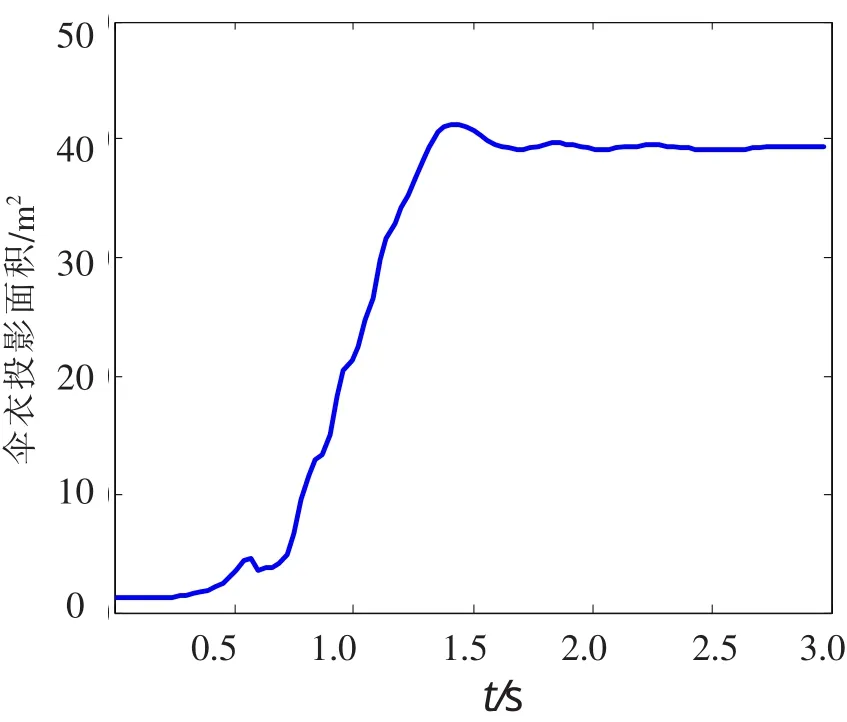
图5 伞衣投影面积曲线Fig.5 Change of projected area
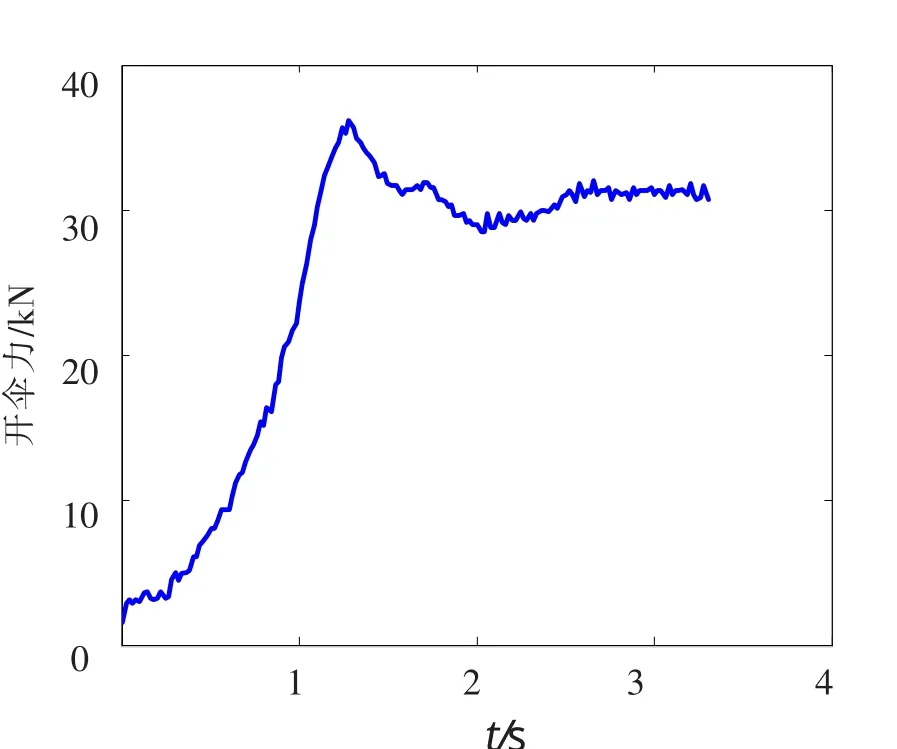
图6 开伞力曲线Fig.6 Change of opening force
图6为降落伞充气过程开伞力曲线,开伞力是指在伞衣充气过程中,降落伞作用在挂重上的力,它是随着充气时间变化的,通常在伞衣充满前达到最大值。本文所计算的最大开伞力为36 092N,文献[1]给出了无限质量情况下最大开伞动载Fkmax的经验公式:
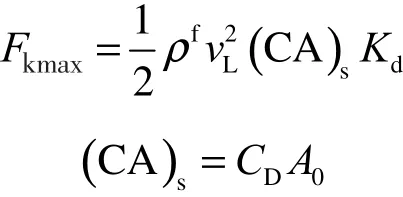
式中Kd称为动载系数,对于一定结构型式的伞衣,Kd是常值,这里参考亚声速范围的开缝伞取值Kd=1.05[15];(C A )s为阻力特征,是其阻力系数与相应的特征面积之乘积,这里阻力特征所对应的特征面积A0取伞衣的名义面积60m2,换算得到对应的阻力系数C为0.63;ρf为大气密度;vL为气流速度。
由图5和图6可看出伞衣自初始充气至首次充满所用时间为1.41s,结合经验公式可对降落伞的充气时间估算,对开缝伞目前还没有实用的解析方法来计算充满时间,文献[15]给出了计算开缝伞充气时间tm的经验公式:
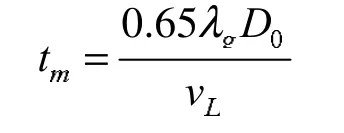
式中 0.65λg实质等于以名义直径表示的伞衣充满距离D0;Ks为伞衣名义直径。由于本文所研究伞型的试验数据资料有限,故参考文献[15]中无限质量条件下降落伞充满距离中平面有缝伞的试验数据,计算得到伞的充满时间为1.398s。
充气过程伞衣周围流场在流固耦合作用下同样会产生较复杂的衍变。图7为流场计算结果的流线变化云图。从图中可以看出在伞衣的阻流体作用下,沿伞衣外缘气流流速明显高于伞衣顶部区域,并在伞顶出现两个涡流,且随着伞衣逐渐充满,涡流随之增长,并由对称分布逐渐衍变为非对称分布。
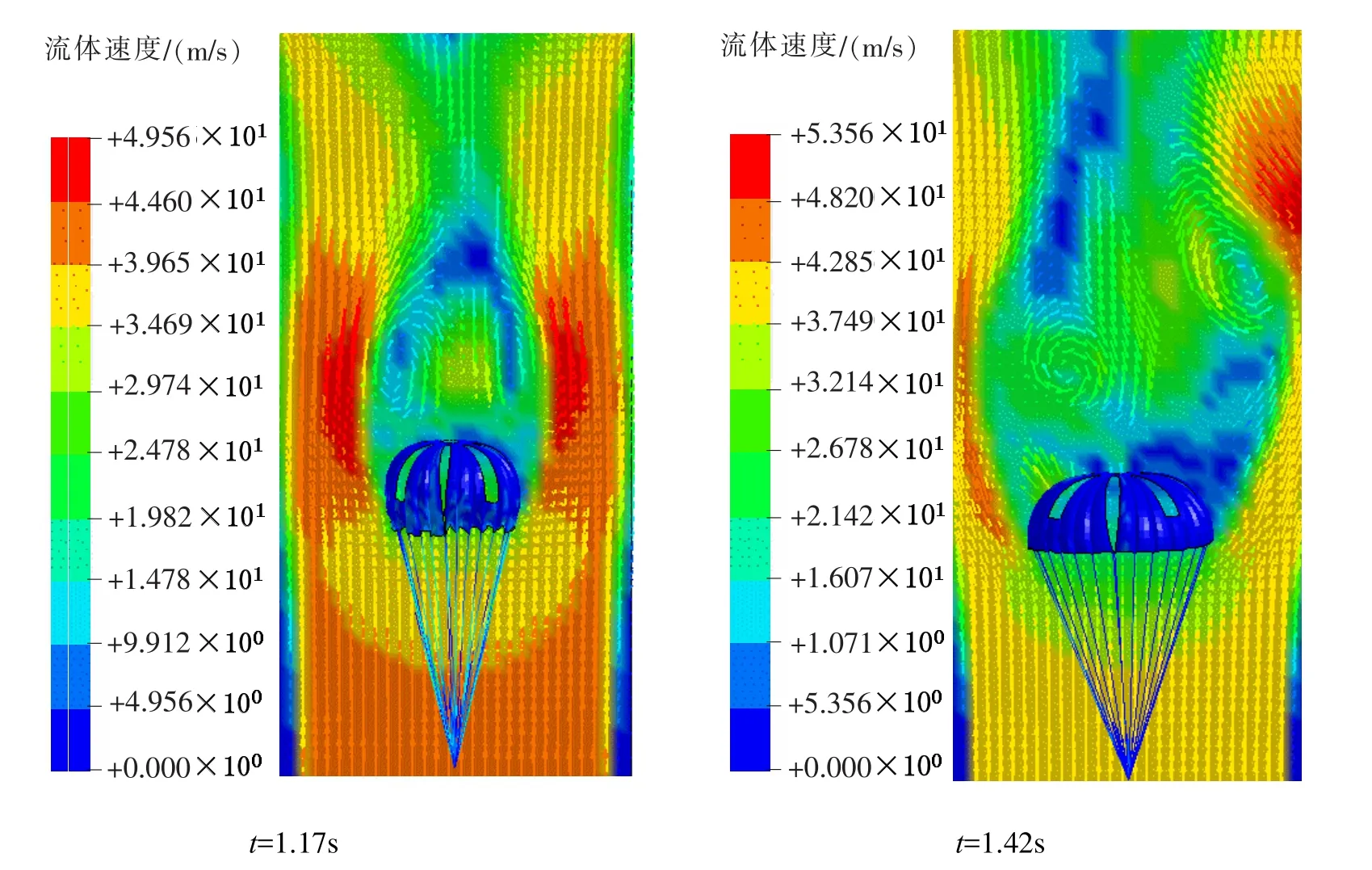
图7 流场流线变化云图Fig.7 Contour of streamlinechange and fluid velocity
计算结果表明:本文所采用的仿真技术有效的模拟了开缝救生伞充气过程的变化特性,包括较大的开伞冲击,伞衣的过度膨胀,尤其是伞衣开缝处的计算结果收敛,未出现不稳定或发散的现象。开缝伞在较高的总透气量下仍保持着可靠的开伞能力,这是由于开缝的流通特性与织物小孔的流通特性不同的缘故,类似具有显著的射流效应的锐缘小孔的功用,因此出现了较大的流通阻力[15]。伞衣周围流场衍变特性复杂,随着伞衣充满,伞衣周围气流不对称性加剧,会影响降落伞充气稳定性。
5 结束语
本文主要针对空投用开缝救生伞的开伞过程进行了研究。针对较为复杂的开缝伞衣结构,基于ALE有限元方法对开缝救生伞充气过程的流体和结构的耦合动力学响应进行了数值模拟,计算得到降落伞充气过程的伞衣外形和开伞力的变化,验证了ALE耦合方法求解降落伞流固耦合问题的有效性,尤其是有缝隙伞衣的耦合结果收敛,对降落伞技术的工程应用具有借鉴意义。本文所采用的技术同样可用于其它型降落伞,如回收伞、航弹伞等的动力学问题研究。
(References)
[1] 王利荣.降落伞理论及应用[M].北京:宇航出版社,1997:102-104.WANGLirong.Parachute Theory and Application[M].Beijing:China Astronautic Publishing House,1997:102-104.(in Chinese)
[2] Vinay K,Tayfun E,Tezduyar.A Parallel 3D Computational Method for Fluid-structure Interactions in Parachute Systems[J].Computer Methodsin Applied Mechanicsand Engineering,2000,190:321-332.
[3] Sathe S,Benney A R,Charles R,et al.Fluid-structure Interaction Modeling of Complex Parachute Designs with the Space-time Finite Element Techniques[J].Computers&Fluids,2005,45(7930):1-9.
[4] Kenji Takizawa Tayfun E,Tezduyar.Computational Methodsfor Parachute Fluid-structure Interactions[J].Arch Comput Methods Eng,2012,19:125-169.
[5] Christine E,Yves DL D P,Pascal B,et al.Fluid-structure Interaction Simulation of Parachute Dynamic Behaviour[C].19th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar,Williamsburg,VA,21-24 May,2007.
[6] 彭勇,张青斌,秦子增.降落伞主充气阶段数值模拟[J].国防科技大学学报,2004,26(2):13-16.PENG Yong,ZHANG Qingbin,QIN Zizeng.Simulation of Parachute Final Inflation Phase[J].Journal of National University of Defense Technology,2004,26(2):13-16.(in Chinese)
[7] 余莉,史献林,明晓.降落伞充气过程的数值模拟[J].航空学报,2007,28(1):52-57.YU Li,SHIXianlin,MINGXiao.Numerical Simulation of Parachute During Opening Process[J].Acta Aeronautica et Astronautica Sinica,2007,28(1):52-57.(in Chinese)
[8] 潘星,胡利,曹义华.降落伞主充气阶段的动态仿真及流场分析[J].航空动力学报,2008,23(1):87-93.PAN Xing,HU Li,CAO Yihua.Analysis of Dynamic Simulation and Fluid Field of Parachute in Inflation Stage[J].Journal of Aerospace Power,2008,23(1):87-93.(in Chinese)
[9] 贾贺,荣伟,陈国良.基于LS-DYNA软件的降落伞充气过程仿真研究[J].航天器环境工程,2010,27(3):367-373.JIA He,RONG Wei,CHEN Guoliang.A Study on Simulation of Parachute Inflation Process Based on LS-DYNA[J].Spacecraft Environment Engineering,2010,27(3):367-373.(in Chinese)
[10] 程涵,余莉,李少腾,等.折叠降落伞展开过程研究[J].航天返回与遥感,2012,33(2):1-5.CHENG Han,YU Li,LI Shaoteng,et al.A Study on the Opening Process of Folded Parachute[J].Spacecraft Recovery and Remote Sensing,2012,33(2):1-5.(in Chinese)
[11] 程涵,余莉,李胜全.基于ALE的降落伞充气过程数值仿真[J].南京航空航天大学学报,2012,44(3):290-293.CHENG Han,YU Li,LIShengquan.Numerical Simulation of Parachute Inflation Process Based on ALE[J].Journal of Nanjing University of Aeronautics&Astronautics,2012,44(3):290-293.(in Chinese)
[12] HUA Cheng,FANGChao.Simulation of Fluid-solid Interaction on Water Ditching of an AIrplane by ALEMethod[J].Journal of Hydrodynamics,2011,23(5):637-642.
[13] Jason W,Nicolas A,Benjamin T,et al.Porous Euler-lagrange Coupling Application to Parachute Dynamics[C].9th International LS-DYNA Users Conference,2005.
[14] Desabrais K J.Velocity Field Measurements in the Near Wake of a Parachute Canopy[D].Worcester:Worcester Polytechnic Institute,2002.
[15]Ewing EG,Knacke T W,Bixby H W.Recovery Systems Design Guide[M].Beijing:Aviation Industry Press,1988.

