整循环图的能量

周后卿，周 琪

（1.邵阳学院数学系，湖南 邵阳422004；2.湖南农业大学经济学院，湖南 长沙410128）

0 引言

设G＝（V，E）是一个n阶简单连通图.用A（G）表示G 的邻接矩阵，A（G）的特征值记为λ1，λ2，…，λn，不妨设λ1≥λ2≥…≥λn.由于A（G）是一个非负不可约矩阵，所以它的所有特征值均为实数，图G 的特征值也就是A（G）的特征值.图G 的能量定义为G 的所有特征值的绝对值之和，即

图的能量最早被I.Gutman引入［1］，它与量子化学之间有着紧密的联系，对分子图而言，能量对应着HMO 意义下的完全π电能.研究图的能量的基本工具是源于Coulson的一个积分公式［2］：

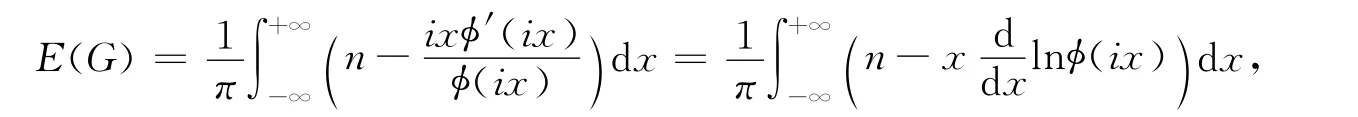
这里φ（x）表示G 特征多项式，φ′（x）是φ（x）的导数.

利用上面这个公式，作为Coulson积分的一个推论，I.Gutman给出了森林的一个简单能量公式：

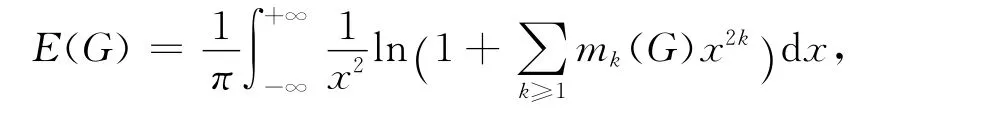
这里，mk（G）表示G 的k 匹配的数目.

从那以后，许多学者对图的能量做了相当广泛而深刻的研究［3］，取得一大批有意义的结论.

例如，对于度为k的n 阶正则图G，R.Balakrishnan证明了图G 的能量的一个上界［4］：

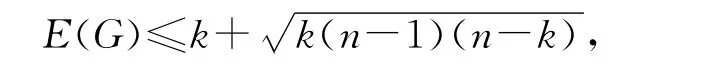
当G＝Kn时等式成立.

利用高斯和，I.Shparlinski给出了一个具有高能量循环图的构造方法［5］；文献［6］研究了Cayley图的能量；文献［7］讨论了整循环图的能量，给出了整循环图Xn（1，pγ）的能量计算公式.虽然许多学者对图的能量进行了卓有成效的研究，但还是有很多悬而未决的问题，R.A.Brualdi就提出了一些开问题，比如：具有n个顶点的图的最大能量是多少？具有最大能量的图是如何构造的？高能量图的构造，超能图的谱半径有多大等问题［2］.本文研究整循环图的能量计算问题.

1 基本概念

一个图叫做循环图，如果它是循环群上的Cayley图，也即它的邻接矩阵是一个循环矩阵.具有n 个顶点的循环图记为G（n，S），它是这样一个图：若它的任意两个顶点i与j 相邻当且仅当i－j（mod n）∈S，S⊆｛0，1，2，…，n－1｝，n为正整数，S＝－S，0∉S，集合S 叫做循环图G（n，S）的符号集.一个图称为整谱图，如果它的邻接矩阵的特征值全是整数.为了便于表述，习惯将整循环图记为ICGn（D）.在过去20年里，整循环图不断出现在编码理论、VLSI设计、Ramsey理论、并行计算和分布式计算中，它在量子物理学中发挥着重要作用.［8］那么，循环图具备什么样的条件，才成为整循环图呢？

设循环图G（n，S）的邻接矩阵为

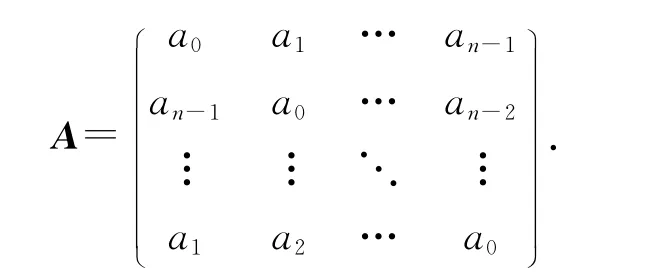
根据文献［9］可知，循环图G（n，S）的特征值为

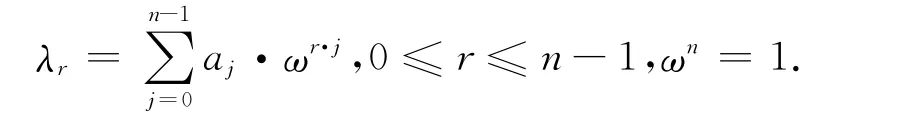
也即

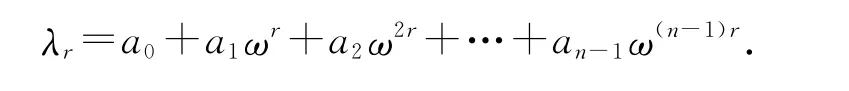
设

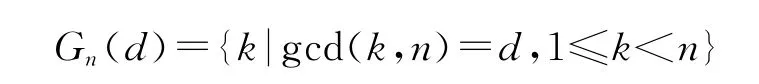
是由小于n并且与n 具有相同的约数的所有正整数组成的集合，这里gcd（k，n）表示k，n 的公因数.令Dn是n 的所有不超过的正约数组成的集合，也即

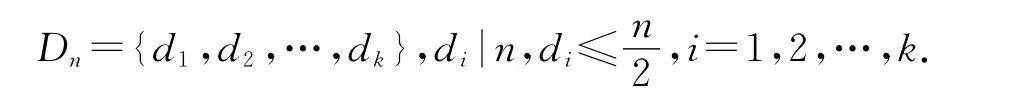
W.So在文献［10］中证明了下列定理：

定理1 一个循环图G（n，S）是整循环图当且仅当S＝∪d∈DGn（d），这里D⊆Dn.

在文献［11］中，W.Klotz和T.Sander证明了整循环图ICGn（D）的特征值为

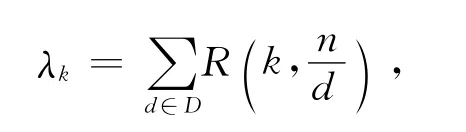
其中

φ（x）表示Euler函数，即

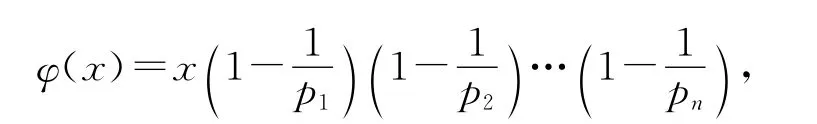
其中p1，p2，…，pn是x 的素因数.

μ（x）表示Mobius函数，即

注意到，对n的任何因数d，下列等式成立：

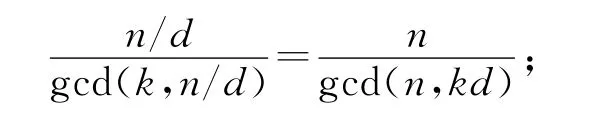
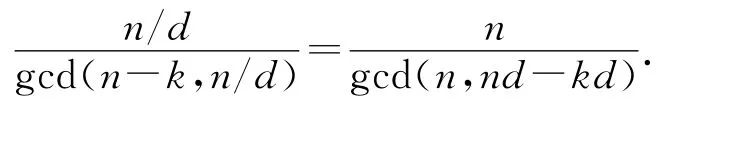
因为

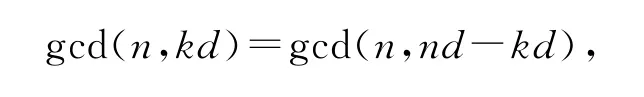
从而有

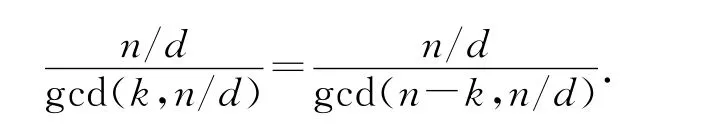
所以

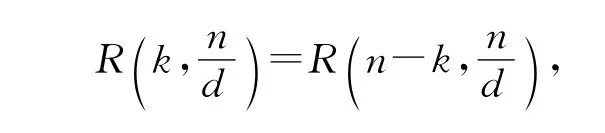
即

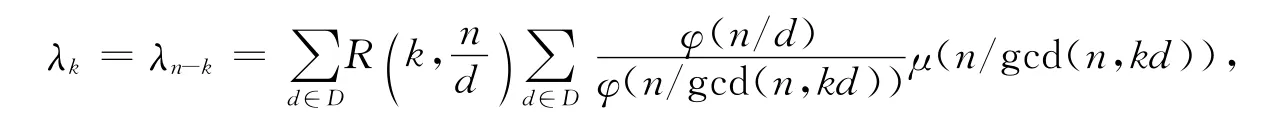
并且

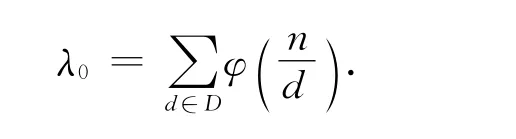
特别地，当n为偶数时，

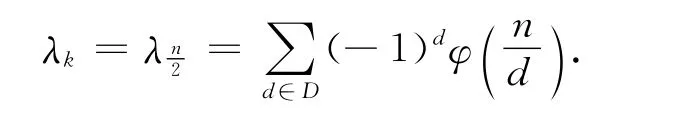
不妨看一个例子.对于顶点数为20的循环图，由于其约数组成的集合Dn＝｛1，2，4，5，10｝，若取D＝｛5｝，即d＝5.则：

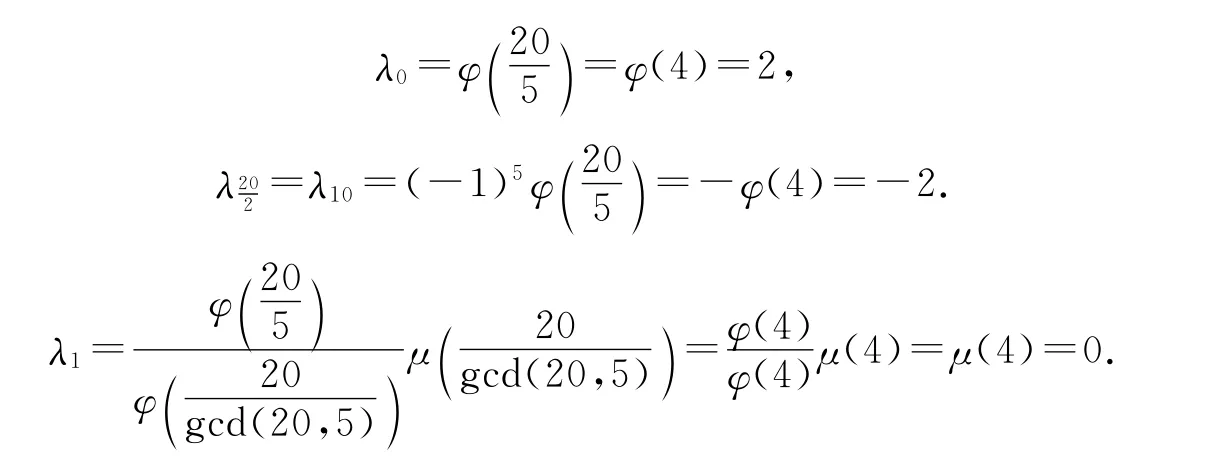
同理可求

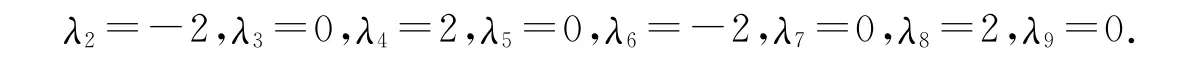
根据λk＝λn－k，得

由此可见，通过Euler函数和Mobius函数求整循环图的特征值，简单可行，不失为一个好方法.

2 主要结论

现在开始研究整循环图的能量计算公式.

若图G＝（V，E）与整循环图ICGn（D）同构，即G≅ICGn（D），则它们具有相同的特征值，因而G 与整循环图ICGn（D）具有相同的能量.不妨设

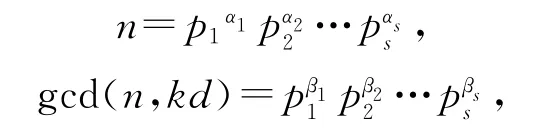
此时

现在分n为偶数和奇数两种情况进行讨论.

情形1 若n为偶数，则

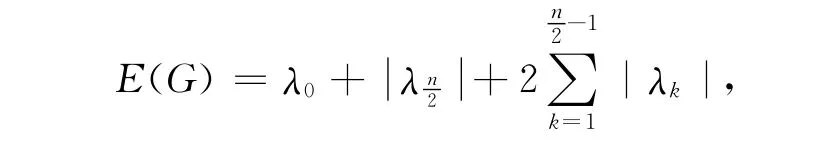
也即

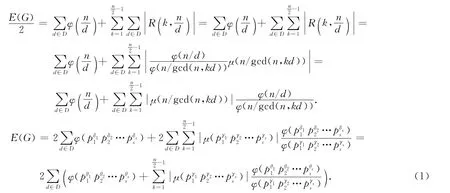
情形2 若n为奇数，则

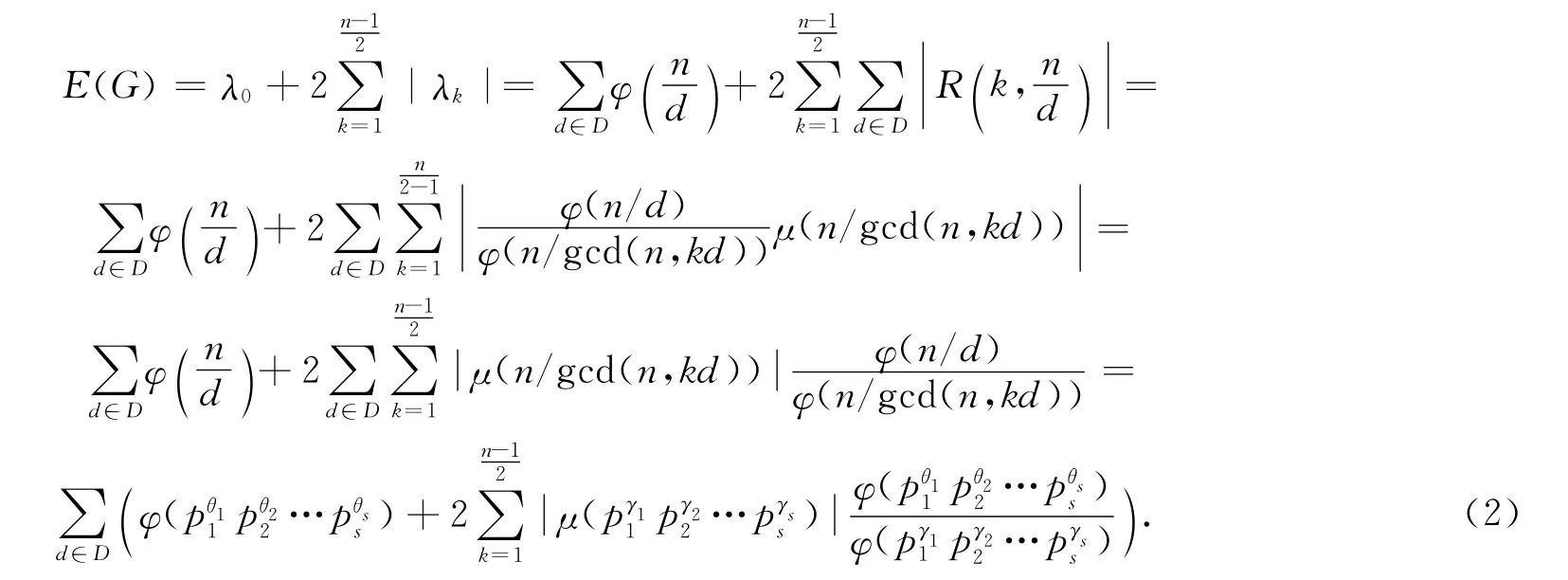
于是得到了本文主要结论：

定理2 设简单连通图G 与整循环图ICGn（D）同构，D⊆Dn＝｛d1，d2，…，ds｝，d1，d2，…，ds为n 的约数，且则图G 的能量为

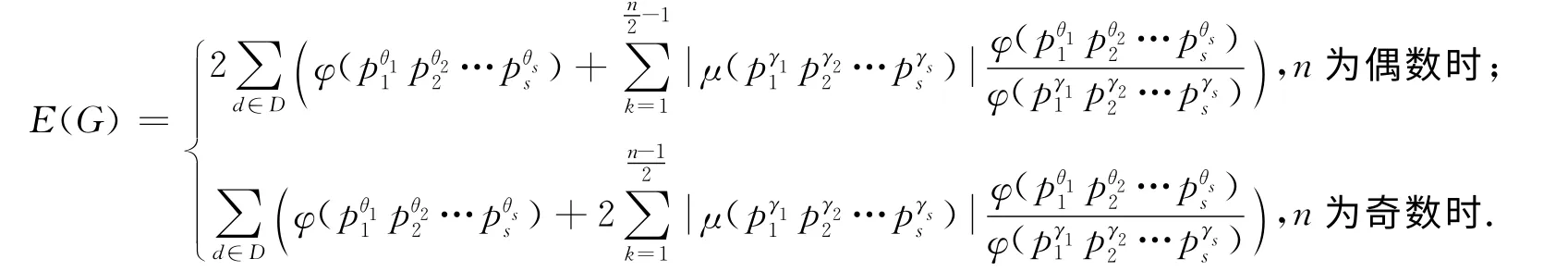
例1 对于顶点为15的整循环图ICG15（D），取D＝｛5｝，即d＝5.则

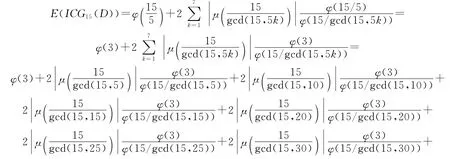
若利用计算软件：Mathematica来求，则可求得循环图ICG15（D）的谱为｛2（5），－1（10）｝.因此得到其能量为20，这个结果与上面用公式（2）计算的结果完全一致，从而也说明了公式的可行性.

［1］GUTMAN I.The energy of a graph［J］.Ber Math Stat Sekt Forschungszent Graz，1978，103：1－22.

［2］BRUALDI R A.Energy of a graph［J／OL］.［2012－01－10］，2006.http：／／www.public.iastate.edu／～lhcgben／energyB.pdf.

［3］GUTMAN I.The energy of a graph：old and new results，in：algebraic combinatorics and applications［M］.Berlin：Springer，2001：196－211.

［4］BALAKRISHNAN R.The energy of a graph［J］.Linear Algebra and its Applications，2004，387：287－295.

［5］SHPARLINSKI I.On the energy of some circulant graphs［J］.Linear Algebra and its Applications，2006，414：378－382.

［6］ILIC A.The energy of unitary Cayley graphs［J］.Linear Algebra and its Applications，2009，431：1881－1889.

［7］ILIC A，BASIC M.New results on the energy of integral circulant graphs［J］.Applied Mathematics and Computation，2011，218：3470－3482.

［8］SAXENA N，SEVERINI S，SHPARLINSKI I.Parameters of integral circulant graphs and periodic quantum dynamics［J］.Int J Quantum Inf，2007，5：417－430.

［9］D AVIS P J.Circulant matrices［M］.New York：John Wiley＆Sons，1979：80.

［10］SO W.Integral circulant graphs［J］.Discrete Mathematics，2006，306：153－158.

［11］KLOTZ W，SANDER T.Some properties of unitary Cayley graphs［J］.Electron Journal Combinatoria，2007，14：45.