井壁漂浮下沉期应变分析

梁旭黎，李方红，杨志江

（1.石家庄经济学院 勘查技术与工程学院，河北 石家庄 050031；2.石家庄经济学院 水资源与环境学院，河北 石家庄 050031；3.中国矿业大学 力学与建筑工程学院，江苏 徐州 221008）

目前在中国钻井法广泛应用于深厚表土层凿井工程中，井筒支护质量的优劣直接影响到整个钻井工程的质量，乃至今后竖井的使用，有关井壁破坏造成重大安全事故的报道屡见不鲜，因此对井壁受力分析的研究意义非常重大［1－4］.本文以河北省唐山市某矿竖井工程为背景，对施工过程中井壁漂浮下沉期井壁的应变进行了弹性力学分析与数值分析，并将二者与实测数据进行了对比，分析了漂浮下沉期井壁应变的变化规律，为深入进行此类研究探索提供参考.

1 工程概况

河北省唐山市某竖井工程采用钢筋混凝土井壁，钻井法施工.地层情况为：0～238.90m主要为砂层和卵砾石层，238.90～251.40m为风化黑云角闪斜长片麻岩，251.40～286.55m为黑云角闪斜长片麻岩.井筒设计净直径为6.2m，井壁结构参数及力学参数见表1.

表1 井壁结构参数及力学参数Tab.1 Structure parameters and mechanical parameters of shaft lining

2 弹性力学分析

在深厚表土层中的井壁是典型的长柱状厚壁圆筒结构，弹性力学中圆筒受均布压力的拉麦公式［5］

式中，σθ，σr分别为计算断面井壁的环向应力和径向应力，MPa；r，R，ρ分别为井壁内、外半径和计算点半径，m；P0为永久地压，P0＝1.2H×10－2，H为地表下一点的深度，m均布压力作用下的内应力分布见图1.

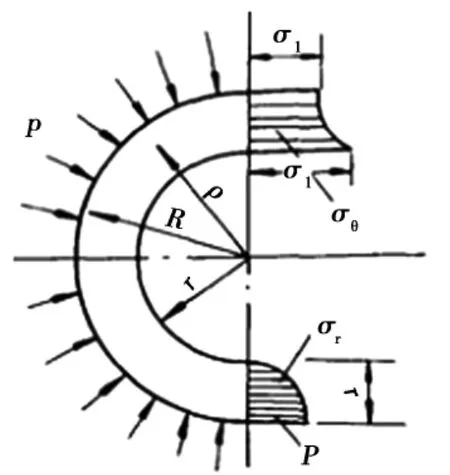
图1 均布压力作用下的内应力Fig.1 Internal stress in the effect of uniform pressure

井壁漂浮下沉阶段，井壁任意水平断面外侧承受泥浆水平压力qn，竖向承受上部井壁自重应力qz，当配重水位超过该水平断面之后，该断面还将在内侧承受配重水压力qw.

泥浆压力计算式为

式中，γn为泥浆重度，由实测确定；Hn为计算断面的下沉深度.

配重水计算式为

式中，γw为配重水重度，γw＝10 000N／m3；Hw为计算断面与配重水之间的距离，m.

式中，W为上部井壁重力，A为断面面积.

因此，井壁任意水平断面圆环应力解为承受内外压厚壁圆筒平面应力的应力解与竖向应力的叠加，即

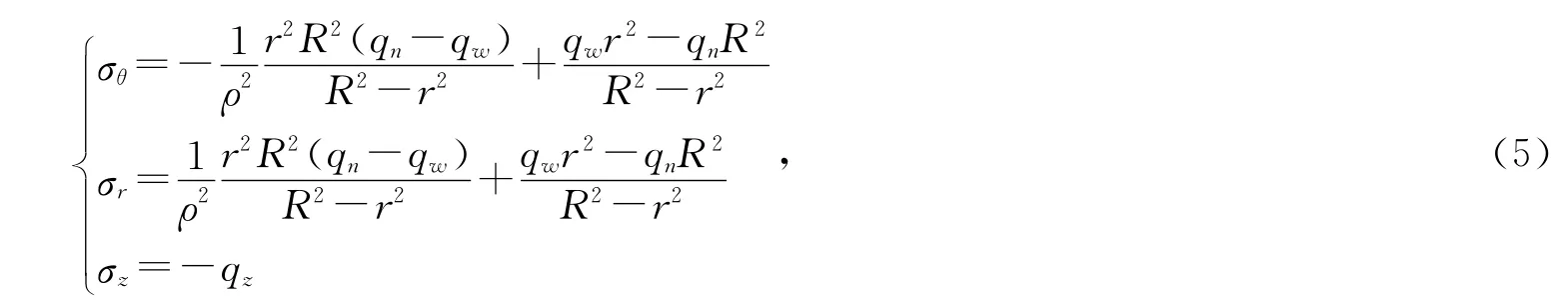
式中，σz为计算断面井壁的竖向应力，MPa.σθ，σr，r，R，ρ同式（1）.

根据轴对称问题的物理方程

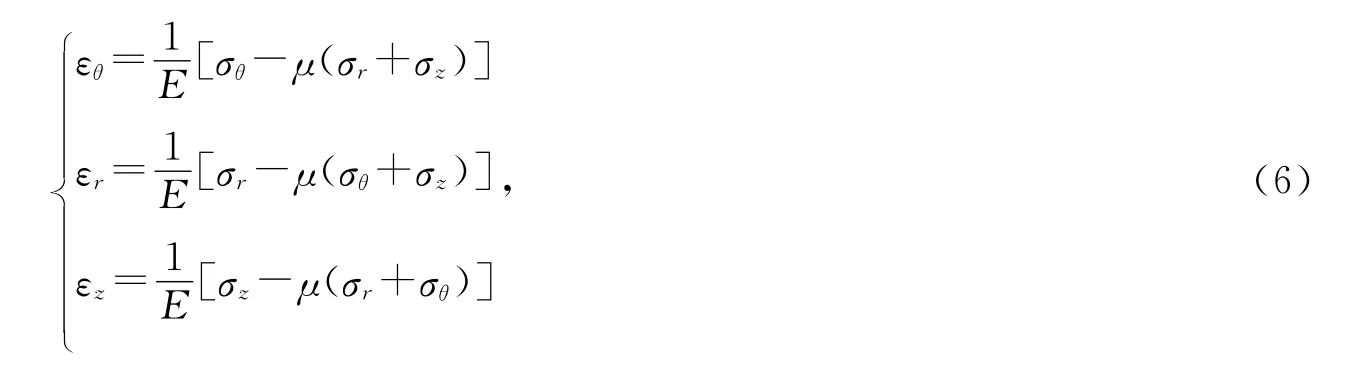
由式（5），（6）可得井壁任意断面应变

式中，εθ，εr，εz分别是计算断面井壁环向、径向和竖向应变；E为井壁混凝土弹性模量，MPa；μ为井壁混凝土泊松比.

由于井壁具有环向受力为主的受力特点，因此以井壁的环向应变计算为例，进行弹性力学求解.全文取第4节井壁中部断面为例，R＝3.7m，r＝3.1m，E＝36 000MPa，μ＝0.2，A＝12.81m2，由式（6）中εθ的表达式可计算出第4节井壁漂浮下沉过程中环向应变的值.井壁任意断面的环向应变值均可用相同方法计算.

例如，当第4节井壁下沉到底时，其中部断面的Hn＝267.5m，根据泥浆对井壁的浮力与井壁的自重和配重水之和相平衡的原理可计算出此时Hw＝180.6m，实测γn＝11 500N／m3，根据施工资料，第5－57节井壁总质量m＝7 525t，计算出qz＝5.91MPa.由式（6）计算出εθ＝－245×10－6.第4节井壁漂浮下沉过程中，其中部断面的环向应变弹性力学计算结果见表2.

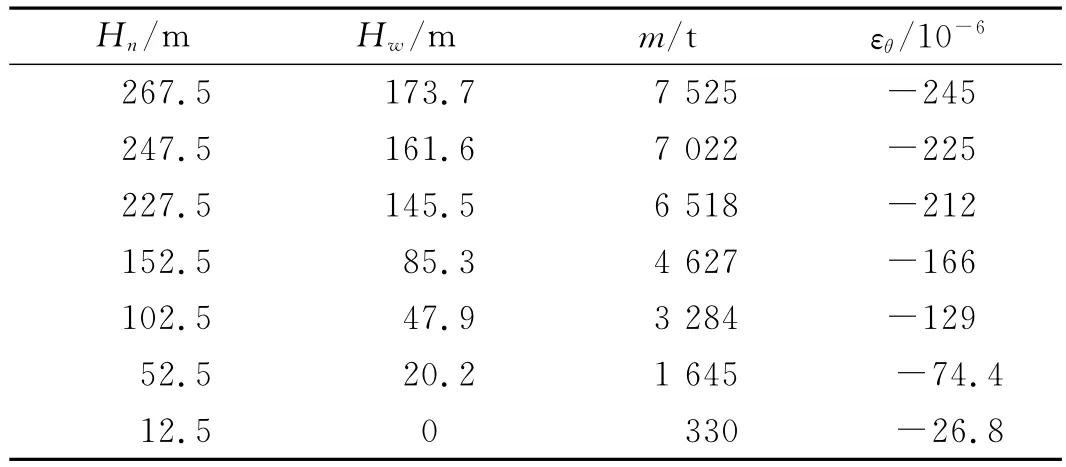
表2 环向应变弹性力学计算值Tab.2 Elasticity calculation values of circumferential strain

3 漂浮下沉过程数值模拟

采用有限元计算软件，就井壁漂浮下沉过程受力做了数值模拟，以便与弹性力学计算值与实测数据进行对比分析.计算采用空间轴对称模型，按实际井壁进行建模，计算模型见图2，有限元网格见图3.各段井壁不考虑钢筋，仅按素混凝土考虑，考虑井壁上下法兰，上下段井壁之间粘接.

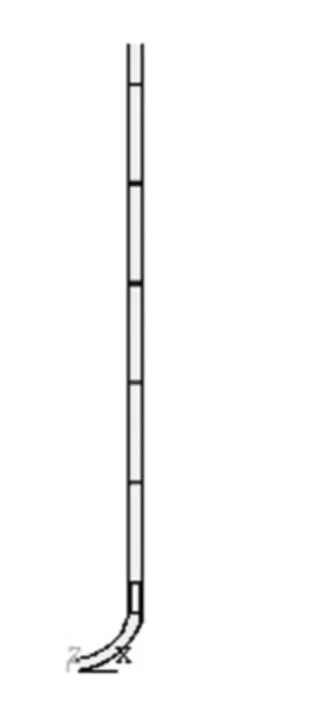
图2 井壁计算模型Fig.2 Calculation model of the shaft lining

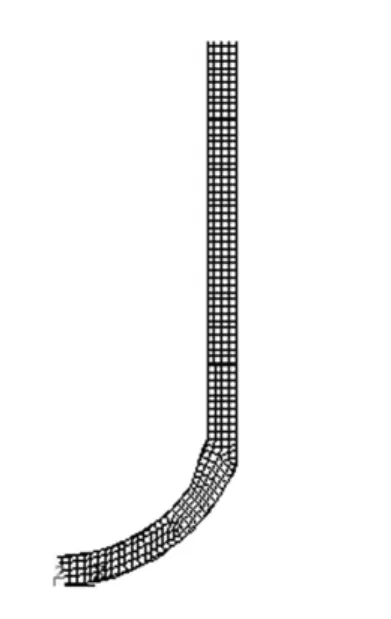
图3 井壁有限元网络Fig.3 Finite element mesh of the shaft lining

井壁几何参数和力学参数见表1.井壁底考虑内外层钢板，不考虑锚卡.钢板弹性模量为210GPa，泊松比0.25，密度7 800kg／m3.

通过数值模拟可获得井壁底钢板和各节井壁环向应变和竖向应变值.

4 计算结果对比与分析

将第4节井壁中部断面环向应变弹性力学计算值、数值计算值与实测值进行对比，见图4.将第4节井壁中部断面竖向应变数值计算值与实测值进行对比，见图5.

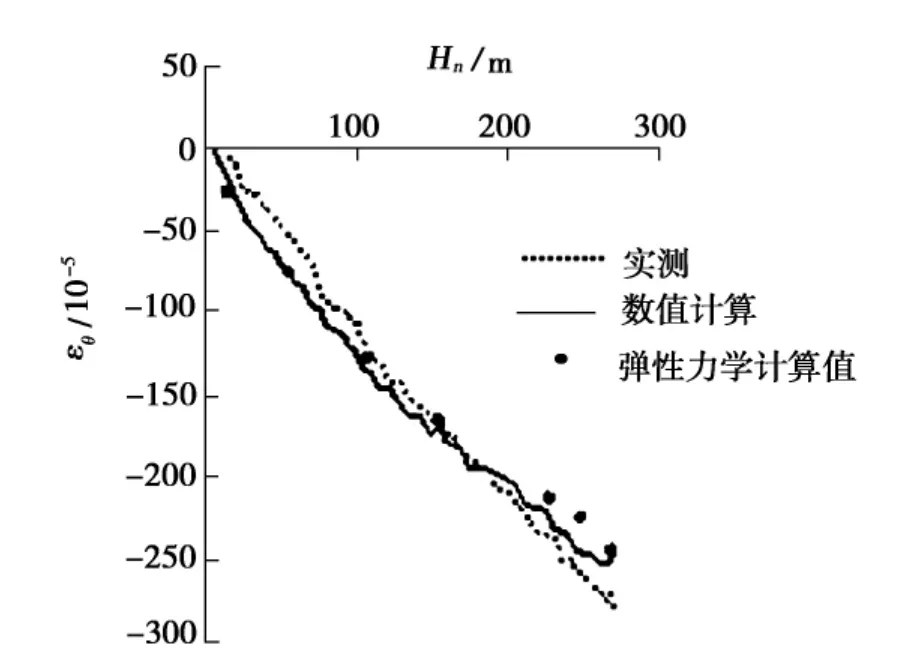
图4 环向应变弹性力学计算值、数值计算值与实测值比较Fig.4 Comparison between elasticity calculation values，numerical calculation curves and measured curves of circumferential strain

图5 竖向应变数值计算值与实测值Fig.5 Comparison between numerical calculation values and measured curves of vertical strain

从图4中看出，第4节井壁中部断面的环向应变弹性力学计算值、数值计算值和实测值均反映出随着下沉深度的加大，环向应变的值也加大，二者几乎呈线性分布；弹性力学计算值、数值计算值和实测值吻合较好.从图5中看出，竖向应变的数值计算值和实测值吻合较好.将图4与图5对比后发现，在井壁的漂浮下沉过程中，环向应变远大于竖向应变，这说明了井壁环向受力大于竖向受力，井壁以环向受力为主，这也是本文以环向应变的弹性力学求解为例来进行应变分析的原因，竖向应变的弹性力学求解方法与环向应变相同.从弹性力学计算值、数值计算值与实测值基本吻合，可以说明本文中所采用的弹性力学计算方法和数值模拟方法均可以对竖井施工中漂浮下沉过程各节井壁的受力进行分析.

井壁底板受力非常复杂，数值计算值与实测值对比后发现差别太大，在本文中不做分析.

5 结论

1）由井壁任意水平断面圆环应变解，对唐山某竖井工程施工中漂浮下沉过程井壁的环向应变进行了弹性力学求解；通过有限元数值计算，对井壁漂浮下沉过程受力做了数值模拟，获得了环向应变与竖向应变解答，环向应变大于竖向应变.

2）将弹性力学计算值、数值计算值与实测值进行了对比，结果表明，弹性力学计算值、有限元数值计算值与实测值基本吻合，均反映出应变值随井壁漂浮下沉深度的增大而增大，二者几乎呈线性分布.

3）井壁的弹性力学计算值、有限元数值计算值与实测值基本吻合，可为类似工程提供参考.井壁底板的有限元数值计算值与实测值相差很大，需要进一步分析.

［1］张永成，孙杰，王安山.钻井技术［M］.北京：煤炭工业出版社，2008.

ZHANG Yongcheng，SUN Jie，WANG Anshan.Drilling technology［M］.Beijing：Coal Industry Press，2008.

［2］崔广心.深厚表土层中圆筒形冻结壁和井壁的力学分析［J］.煤炭科学技术，2008，36（10）：17－21.

CUI Guangxin.Mechanical analysis on cylindrical freezing wall and mine shaft liner in deep thick overburden［J］.Coal Science and Technology，2008，36（10）：17－21.

［3］杨志江，梁旭黎，王华明，等.施工期钻井井壁混凝土应变实测分析［J］.煤炭学报，2011，36（9）：1463－1468.

YANG Zhijiang，LIANG Xuli，WANG Huaming，et al.Insitu measurement and analysis of drilling shaft lining concrete strain during sinking［J］.Journal of China Coal Society，2011，36（9）：1463－1468.

［4］牛学超，洪伯潜，杨仁树.充满配重水钻井井壁筒在泥浆中竖向结构稳定的理论研究［J］.煤炭学报，2005，30（4）：463－466.

NIU Xuechao，HONG Boqian，YANG Renshu.Theory study on axial structural stability of bored shafts filled with water［J］.Journal of China Coal Society，2005，30（4）：463－466.

［5］徐芝纶.弹性力学［M］.北京：高等教育出版社，2005.