岩石硬性结构面粗糙度量化及其剪切试验研究

潘 凯,谭 洵,吉 锋,蔡国军

(1.成都理工大学环境与土木工程学院,四川成都610059;2.成都理工大学地质灾害防治与地质环境保护国家重点实验室,国家级地质工程试验教学示范中心,四川成都610059)

0 前 言

结构面的力学特性是决定工程岩体稳定程度的重要因素[1],对于评价和研究岩石结构面力学特性,精准测量岩石结构面的粗糙度显得尤为重要,如何获得精准的结构面粗糙度值是本文的研究重点。结构面在剪应力作用下的变形及强度特征,根据受力后的变形及破坏机制,可将结构面分为平直光滑无填充、粗糙起伏无填充、非贯通断续及软弱物质填充四种情况[2]。对于充填度较小的硬性结构面,表面形态是影响结构面力学性质的决定性因素[3]。研究岩体硬性结构面表面形态及其与结构面力学特性的内在关系,得出合适的剪切数学模型,具有重要的理论意义和工程实用价值。前人为剪切模型以适应岩体强度特点,在库伦定理的修正上做了大量贡献:挪威学者Barton对结构面起伏形态开展了深入研究,建立10条标准曲线,并提出工程界广泛采用的JRC-JCS剪切模型公式[4]。据调研,目前实际计算岩石结构面粗糙度,多数仍是参照Barton 10条标准曲线对JRC进行估计,鲜见对岩石结构面表面粗糙度JRC值进行量化和精确测定,造成与结构面真实JRC值存在较大误差。在此背景下,本文运用接触打孔器[5]对岩石二维起伏形态进行了测绘,将特定分度的横向网格对不同JRC的起伏曲线进行覆盖并统计交点数,通过大量的数理统计和数值模拟以发现交点数Nr与JRC之间的关系后,以Barton定义的10条标准JRC曲线[6]为研究对象,依次建立了Nr-JRC的函数公式和基于结构面表面形态二维的剪切强度估算公式,从而达到对岩石硬性结构面粗糙度JRC值较为精确的量化计算的目的。并通过岩石结构面剪切试验验证了该模型的合理性。

1 岩石硬性结构面剪切模型

1.1 Barton JRC-JCS经典模型

Barton在研究中考虑了裂隙面的粗糙度和组成裂隙壁的岩石的强度对岩体裂隙强度的控制意义,在对几百条裂隙进行试验研究的基础上提出了岩石结构面剪切强度方程[7]:

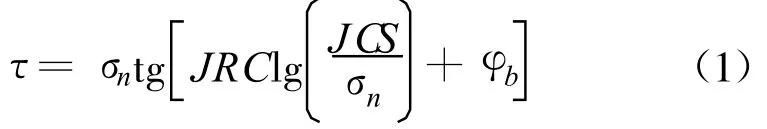
式中:σn为法向主应力;τ为剪切应力;JCS为壁面岩石强度;φb为基本摩擦角;JRC为结构面粗糙度系数。

1.2 Barton经典模型中各参量的选取

式(1)中JCS是结构面两壁表面岩石的单轴抗压强度值,在两壁岩石轻微风化的情况下,可以采用岩芯或块石进行常规单轴抗压试验或点载荷试验求出;当两壁岩石风化强烈时,岩块的抗压强度不能反映两壁表面岩石的强度,这时可以通过回弹试验求得。根据回弹测定的Re值,用以下经验公式[7]求得隙壁岩石的抗压强度。

式中:ρd为所测岩石的干密度(g/cm3)。

基本摩擦角φb指非剪胀平直面的残余摩擦角,可以按经验数据或者通过对试件的锯开面进行倾斜滑动试验求得,还可以通过对未风化平直光滑结构面进行直剪试验[7]来估算获得。

对于剪切强度公式中另外一个重要参数结构面粗糙度系数JRC,要精确得到其值是比较困难的,杜时贵(1992)等人设计的节理表面形貌测绘仪[8],取结构面曲线样与Barton 10条标准曲线进行对比,得到粗糙度的取值范围;吉锋博士(2008)研制出一种便携式测量仪器—接触打孔器[9],该仪器采用接触打孔原理,实现了硬性结构面精细测量的机械化,提高了野外工率,如图1。

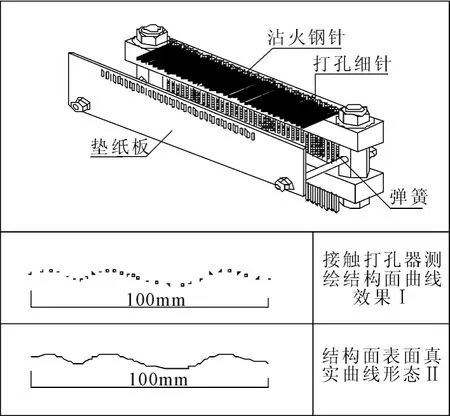
图1 接触打孔器示意图

JRC值的测取误差往往来自于结构面曲线的测绘与估算,常常由于人为原因产生较大的差异,所以探求精度更高的JRC值是有意义的。本文通过网格覆盖法和数理统计建立了结构面粗糙度JRC与Nr的关系预测模型,通过回归曲线建立一个Nr—JRC函数公式,对传统的JRC计算公式进行了改进和优化,为研究硬性结构面起伏形态和量化岩石粗糙度提供了一种有效的理论新途径。

2 网格法探求粗糙度计算模型

在研究过程中用接触打点器采取到结构面剖面曲线的二维坐标(X,Y),将数据用插值法导入CAD绘图软件获得曲线图形,将这些曲线分别与预先建立的10 cm长的横向网格图块叠合,可观察到曲线与横向网格的直线交点明显易数,从所得的数据中发现JRC值越大,交点数就越多,基本示意图如图2所示,部分数据记录如表1。

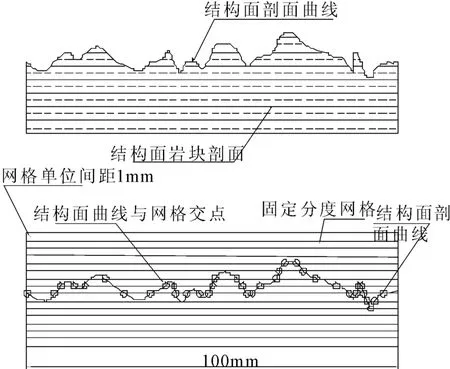
图2 结构面与标准网格交点示意图

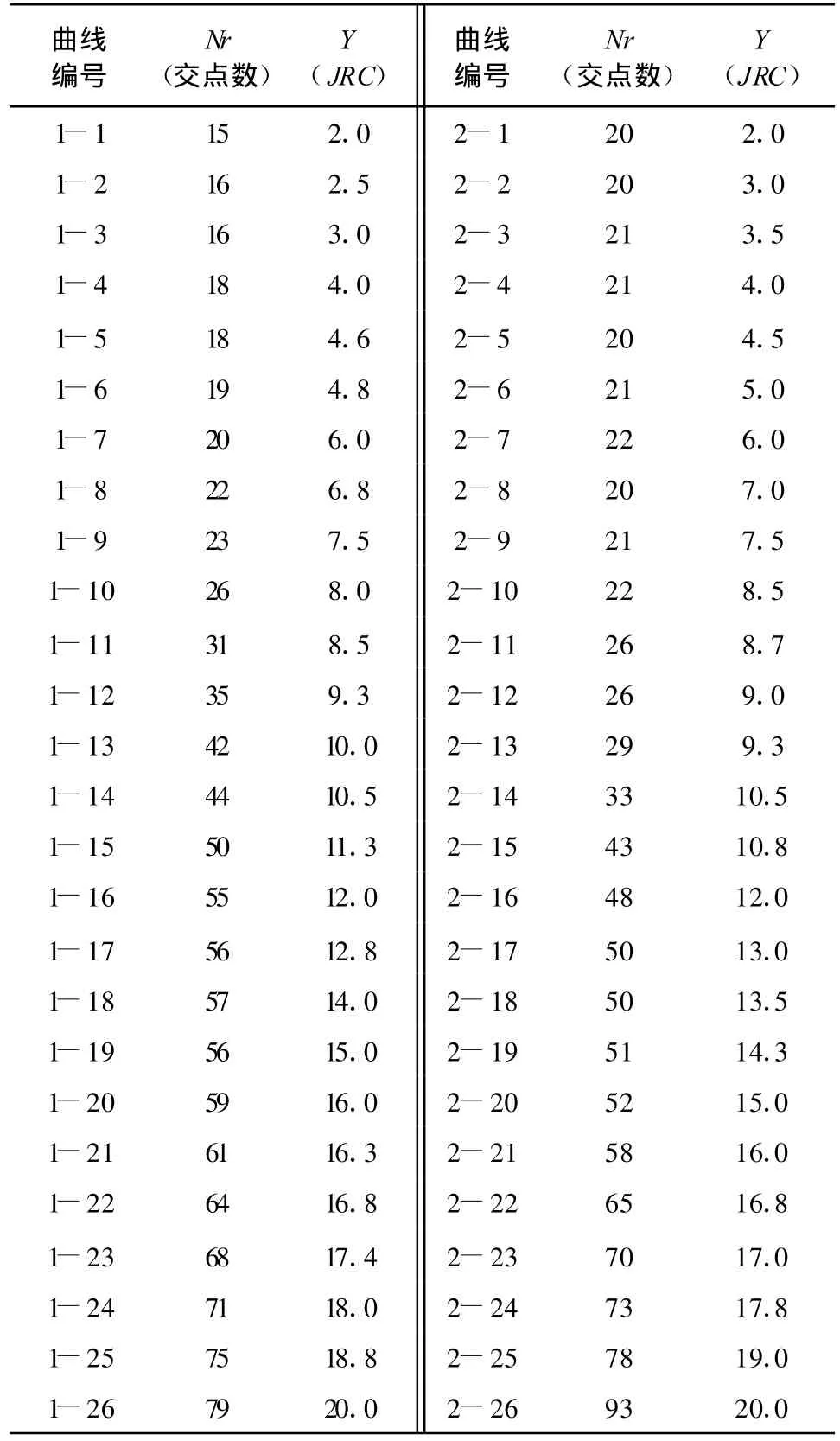
表1 (JRC-Nr)部分数理统计数据

为量化寻求JRC值与交点数的关系,以交点数为Nr,JRC值为Y,将散点(Nr,Y)导入MATLAB中,进行线性回归分析得回归曲线,经过大量试验和数理统计得到类似图像,如图3;所以,虽然采集的样本和实验有限不能反映全貌,但根据大量的统计规律可以合理推理推测:JRC值与网格交点数Nr之间有较为显著的线性关系。

3 建立表征结构面粗糙度的理论函数

3.1 获取交点数

已知10条10 cm Barton标准结构面轮廓曲线,运用2中的方法,使曲线图形与一定标度的横向网格叠合(如图4),统计曲线与网格直线的交点数Nr,为消除不同网格间距对小范围曲线起伏带来的误差,做如下处理:将所得的轮廓曲线分别与横向间距gi(gi=0.1,0.3,0.5,1,2,3,4,5,10 mm)的网格进行叠合统计交点,找出交点数增加价位稳定的间距区段网格,经过大量的对比分析,笔者发现单位网格间距gi=1 mm区段较为合理。统计标准曲线交点数据如表2,其中X取两相邻JRC曲线交点数Nr的平均值。

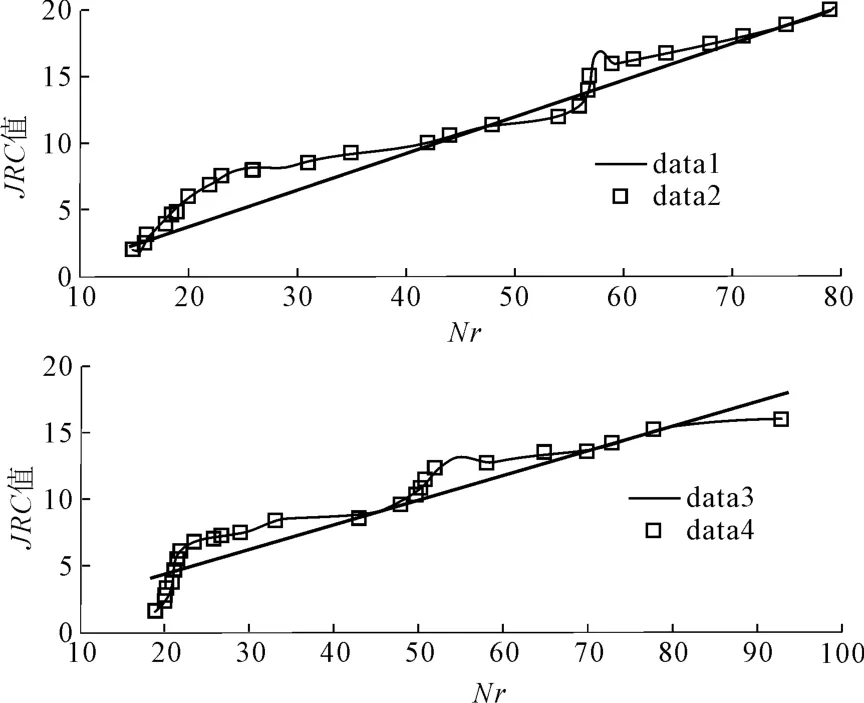
图3 数理统计曲线

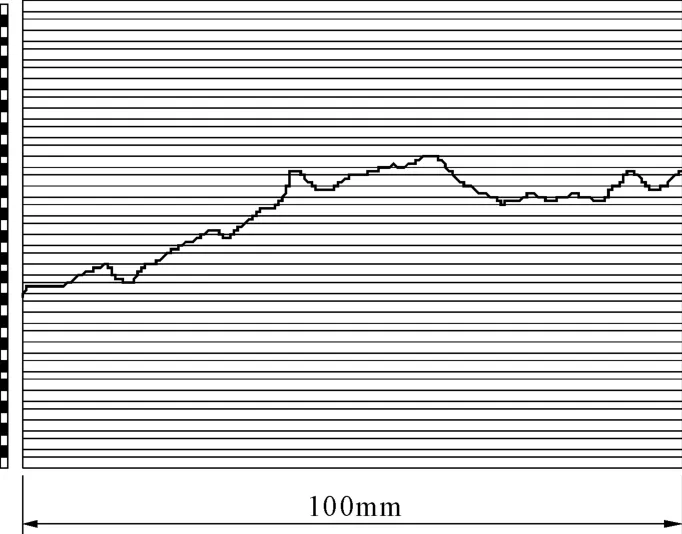
图4 JRC值8-10的标准曲线与网格叠合图

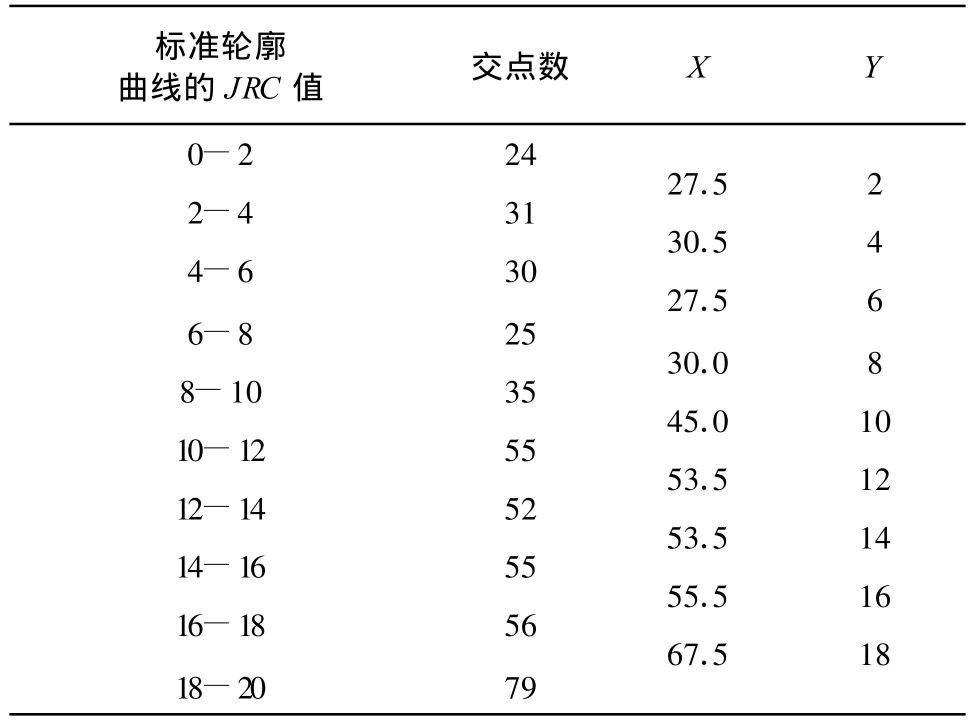
表2 10条Barton标准轮廓曲线交点数统计表

3.2 回归分析拟合函数

将数理统计所得的数据进行线性回归,并根据寻找特征点建立相应函数Y=0.347886X-5.092,以Nr代替X值,JRC代替Y值,则JRC的网格交点预测函数为:JRC=0.347886Nr-5.092,R2=0.9,回归曲线合理。

3.3 将网格交点预测函数引入Barton经典模型

将所得预测函数带入Barton JRC-JCS经典模型式(1),用参数Y替换模型中的JRC,于是就得到新的岩石硬性结构面强度公式:

式中各参量的选取如前所述。

3.4 试验验证与实例分析

为了模型的合理性,本次试验采取一段高速公路开挖面上的新鲜紫红色砂岩和微风化砂岩硬性结构面作为试验对象,通过上述的方法测定结构面面壁起伏曲线与网格的交点数Nr,用现场回弹试验测定裂隙两侧岩石抗压强度JCS,用倾斜试验测基本摩擦角 φb,精确得到三个指标后运用该公式按不同级别的正应力 σn值计算出τ值,绘制σn-τ曲线,从而根据 σn-τ曲线得到c和φ。如表3所示计算值,与室内的直剪试验结果相对比,误差(平均误差＜15%)较小,计算值与试验值比较接近,从而充分验证了改进模型计算的可靠性。

表3 公式计算结构面强度与直剪试验结果对照表

4 结 论

本文以岩石硬性结构面为研究对象,研究了影响结构面强度的重要因素之一:硬性结构面表面起伏形态,主要成果如下:

(1)合理推测了结构面表面起伏度与网格交点数呈线性关系,运用网格法并采用交点数Nr来刻画结构面表面形态起伏度。

(2)以10条Barton标准结构面轮廓曲线为基础,运用网格法得到结构面表面形态起伏度与JRC值之间的函数关系式:JRC=Nrtgθ+K,将所得新函数带入原始Barton二维岩石结构面强度公式,替换相应变量,得到新的岩石硬性结构面强度公式,并验证了该公式有一定的可靠性。

[1] 孔德坊.工程岩土学[M].北京:地质出版社,1992:83-91.

[2] 肖树芬.岩体力学[M].北京:地质出版社,1999:49-59.

[3] 孙广忠.岩体结构力学[M].北京:科学出版社,1988:198-220.

[4] Barton N,Choubey V.The shear strength of rock joints in theory and practice[J].Rock Mechanics,1977,10(1-2):1-54.

[5] 吉 锋,石豫川.硬性结构面表面起伏形态测量及其尺寸效应研究[J].水文地质工程地质,2011,38(4):63-68.

[6] Barton W E.Suggested methods for the quantitative description of discontinuities in rock masses[J].Int J Rock Mech Min Sci&Geomech Abstr,1978,15(6):319-368.

[7] 孔德坊.工程岩土学[M].北京:地质出版社,1992:118-119.

[8] 杜时贵.结构面与工程岩体稳定性[M].北京:地震出版社,2006:64-68.

[9] 吉 锋,石豫川,冯文凯.一种新型的结构面起伏形态测量工具——接触打孔器的研制[C]//第三届全国岩土与工程学术大会论文集.岩土与工程新技术新方法,2011.