柱形爆炸容器安全概率的区间估计＊

刘 钰，韩 峰，董 楠，陆希成，雷 鸣

（西北核技术研究所，陕西 西安710024）

爆炸容器用于封闭高能炸药的爆炸效应，限制爆炸冲击波和爆炸产物的作用范围，对人员和设备实现有效防护，便于实验观测和测试的安全，并保护环境。爆炸容器的优异性能使其广泛应用于爆炸加工、科学研究、特种物质运输、新材料研制等多个领域［1］。由于爆炸容器需要承受一定当量的爆炸冲击波和封闭爆炸产物，所以应关注爆炸容器的安全性。

当前爆炸容器的设计主要采用工程设计、数值模拟、实验验证的思路。一般的容器设计方法，是在给定的爆炸载荷条件下，计算容器需要承载的最大载荷并增加一定的安全裕量，进而确定容器的壁厚，最后通过实验评估容器的安全性。如常用的动力系数法［2－3］，或基于塑性变形的设计方法［4］。但爆炸容器实验装置是一个复杂系统，在研制和实验过程中不可避免地会受到各种随机因素的影响，如爆炸载荷和屈服强度等［5－6］。上述确定性设计方法中，没有考虑影响容器安全的不确定性因素，会使容器安全裕量设计得过大且实验成本较高。而基于随机性分析的爆炸容器安全评判方法，可以分析并量化随机因素对爆炸容器安全的影响，进而估计爆炸容器的安全概率。

本文中，基于爆炸容器安全的概率评判方法，研究爆炸容器的安全概率区间估计问题，并以柱形容器为例，给出计算容器安全概率区间估计的一般方法。

1 数值模拟结果的统计分析

1.1 实验对象及数值计算

在本文的数值计算中，爆炸装置爆炸后的状态及产生的力学效应和爆炸产生的力学效应与周围介质的相互作用，被作为一个整体使用动力学分析软件进行研究，爆炸及其力学效应使用Euler方法描述，容器及其他结构的变形采用Lagrangian方法描述，相互之间的作用采用流固耦合技术处理［7］。由于单层柱形容器结构相对简单，有利于研究在不同当量TNT 炸药爆炸下变形和破坏的概率，选择某单层柱形容器作为研究对象，其剖面结构示意图如图1所示。

图1 柱形容器结构示意图Fig.1Sketch of cylindrical vessel structure

炸药的半径和长度取决于当量，容器内半径为6cm、厚度1cm、半长30cm。在8种不同TNT 炸药当量下，对质量比内能及切线模量进行了拉丁超立方抽样，获得了100组计算参数，并计算得到了数值模拟结果，即变形量xr的随机样本，部分数据的直方图如图2所示。

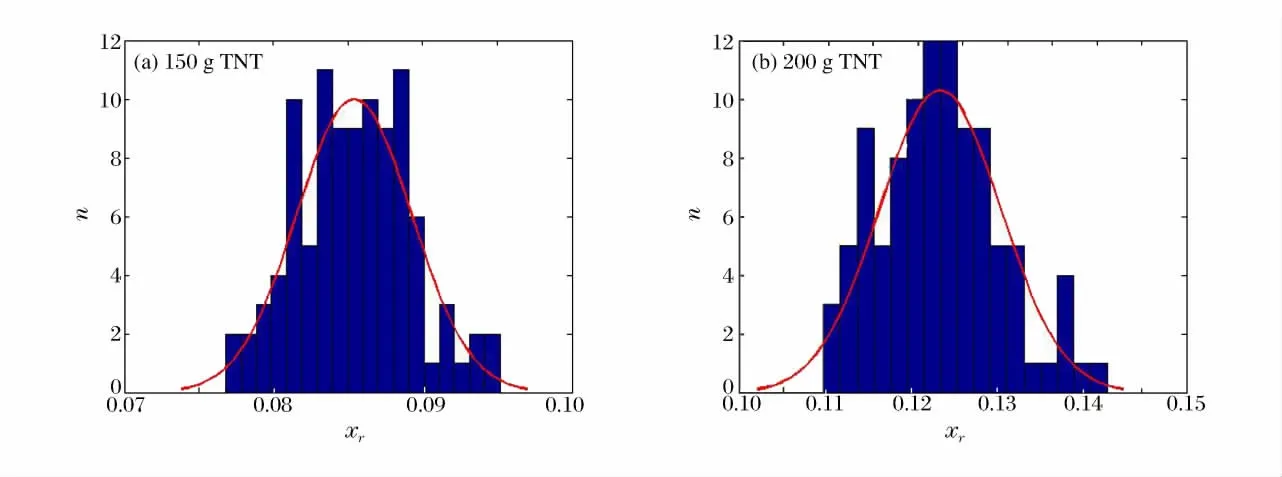
图2 部分爆炸当量下容器径向变形量直方图Fig.2 Histogram of radial distortion of the vessel with different TNT equivalentce

1.2 数值计算结果的概率分布检验

从直方图观察，可以假设xr服从正态分布、对数正态分布、Beta分布以及Weibull分布，然后对给定的显著性水平α，通过柯尔莫哥洛夫检验法［8］（KS检验）对径向变形量数据进行分布检验。原假设为

式中：Xi表示样本。

检验方法是使用KS统计量Dn与检验临界值Dn，α进行比较，若Dn＞Dn，α，则拒绝H0，否则接受H0。其中检验统计量Dn是样本顺序统计量X（i）频数分布与假设分布偏差的最大值，再通过计算得到临界值Dn，α。在显著性水平为α＝0.01下，对不同TNT 当量WTNT径向变形量数据进行了分布检验，如表1所示。

表1 置信度1－α ＝0.99和样本量n ＝100时KS检验结果Table 1 The results of KS test with the confidence 1－α ＝0.99 and sample size n ＝100

从表1可见，除了Weibull分布检验P 值明显较小外，其他3种分布都可以描述各当量下径向变形量数据的不确定性。但是，正态分布的检验P 值是几种分布中最大的，因此，径向变形量数据服从正态分布的可能性最大。在此基础上，可以进一步通过Lilliefors检验法［8］对径向变形量数据进行正态性检验。原假设为

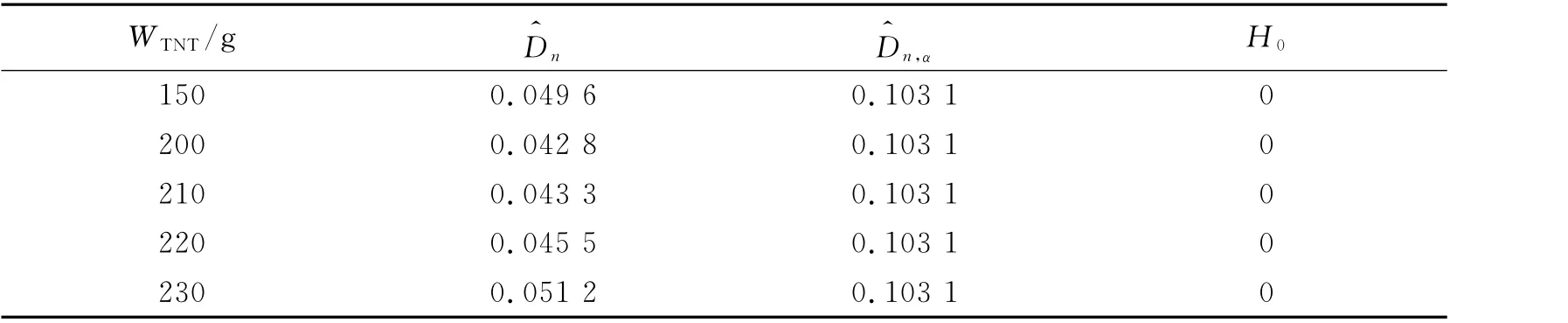
表2 置信度1－α ＝0.99和样本量n ＝100时Lilliefors检验结果Table 2 The results of Lilliefors test with the confidence 1－α ＝0.99 and sample size n ＝100

这样，经过KS检验以及Lilliefors检验，认为径向变形量数据是服从正态分布的。对于未知总体的概率分布估计问题，还可以使用最大熵方法进行估计［9］。

1.3 正态分布参数区间估计

设爆炸容器变形量xr服从N（xr，μ，σ）分布，其概率密度函数为

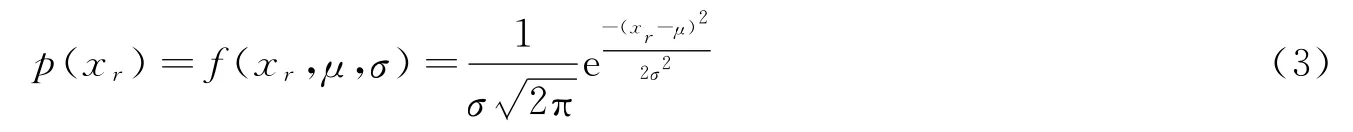
式中：μ 和σ 为分布参数，且σ ＞0［10］。

在考虑置信度要求下，一般使用参数的区间估计方法。对于正态分布，该总体的均值μ 和方差σ2都未知［11］，则在置信水平为1－α 下，μ 的区间估计为

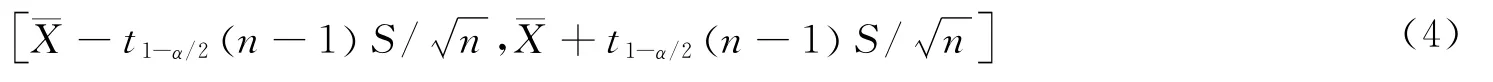
σ2的区间估计为

1.4 安全概率P（D）的区间估计

对任意给定的变形量D，安全概率P（D）服从正态分布，分布参数为μ 和σ，可以通过参数μ 和σ的区间估计来分析P D（）的置信区间。

分析正态分布函数随参数σ（或μ）的变化情况，如图3（a）所示，如果随机变量x ＞μ0，则概率是参数σ 的减函数；如果x ≤μ0，则概率）是参数σ 的增函数。同理可分析，图3（b）显示，概率P （x ，μ ，σ0）是参数μ 的减函数。

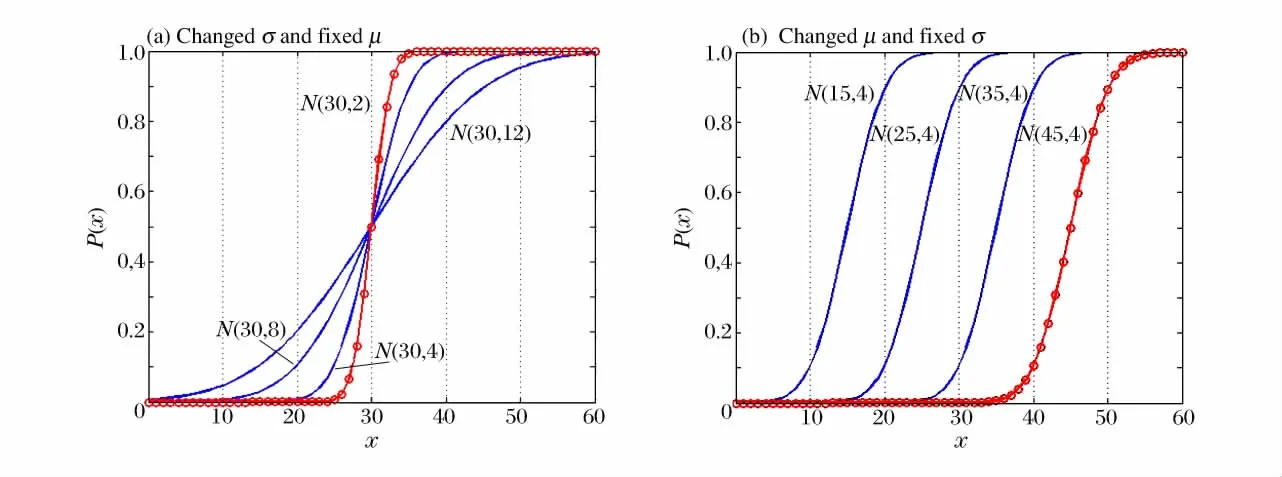
图3 正态分布随单参数变化规律示意图Fig.3 Plot of normal CDF with the change of single parameter

在双参数坐标空间内，对给定随机变量x0，当μ ＜x0时随参数σ 增大而减小，随参数μ 增大也减小；当μ≥x0时，P （x0，μ，σ）随参数σ增大而增大，随参数μ增大仍减小，这与前面的分析结果是一致的。从而可以看出P （x ，μ，σ）在μ 和σ 的取值空间上关于x 是单调递增的，如图4所示。

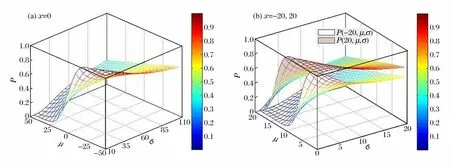
图4 正态分布随双参数变化规律示意图Fig.4Surface plot of normal CDF with the change of both parameters

由于x 在参数μ的两侧时，P （x）与参数的单调性关系是不同的，参数μ又在区间上变化，根据x 和μ 的大小关系，可以分段给出P（x）的上、下限函数

则由式（6）～（8）可计算得到，在置信度1－α 下，安全概率P D（）的置信区间为［PLD（），PUD（）］。

P（x）的函数图像如图5所示。图5（a）为不同参数组合下P D（）函数的图像，其中aL、aU分别表示分布参数的上、下界。图5（b）是图5（a）中曲线的包络，图中标出了在D 取值不同时，不同参数组合下P D（）函数的上、下限。同样，也可以通过优化方法计算P D（）的区间估计。

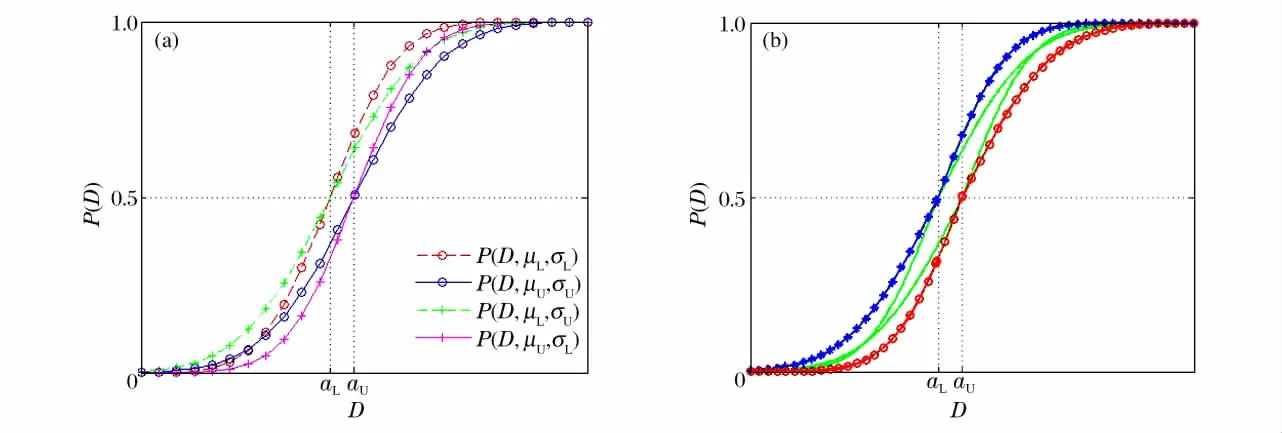
图5 在置信度为1－α ＝0.95下，P（D）的上、下限函数图Fig.5 The upper and lower limits curve of the P（D）with the confidence intervals 1－α ＝0.99

2 柱形容器安全概率的区间估计

根据以上统计分析方法，可以对柱形容器在不同TNT 爆炸当量下，100组容器径向变形量数值模拟数据进行统计分析。

对于给定变形量要求D ＝15%，在置信度1－α ＝0.95 下，考察径向变形量xr＜D 的概率的置信区间为，结果如表3所示。

表3 置信度1－α ＝0.95时安全概率P（15%）的置信区间Table 3 The confidence intervals of the security probability P（15%）corresponds to1－α ＝0.95

显然，对于给定变形量D＝15%，在置信度1－α＝0.95下，随爆炸TNT 当量变化，柱形容器径向变形量xr＜15%的概率具有明显变化。那么可以反过来考察，如果要求在置信度1－α＝0.99下，对不同当量TNT 爆炸，柱形容器径向变形量xr不超过Di（i＝1，2，…，8）的概率下限PL（Di）＝0.999，则可以计算出不同当量下的Di，如表4所示。

表4 安全概率PL（Di）＝0.999对应的给定变形量Table 4 The radial distortion threshold corresponding to the security probability PL（Di）＝0.999

此时各当量下，径向变形量以最小有99.9%的概率小于Di，且这个结论的置信度为99%，这样的结论已经是相当可靠的了，那么此时计算得到给定变形量的下限可以作为衡量实验安全的判据。

3 结 论

综上所述，在爆炸容器设计完成后，该容器安全概率的区间估计与爆炸载荷具有一定的相关性：

（1）TNT 当量与Di是近似线性的，说明炸药当量越大，径向变形量上限也越大，容器安全性越低，如图6所示。

（2）随着TNT 当量的增大，容器的安全概率将逐渐降低，对应的（在一定置信度下）概率上下限也逐渐降低，且分散性（不确定性）增大，如图7所示。

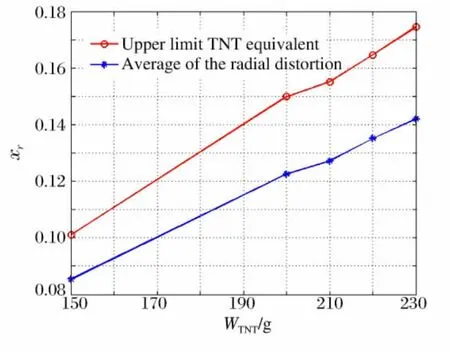
图6 TNT 当量与径向变形量的关系图Fig.6 The relation between the radial distortion and TNT equivalence

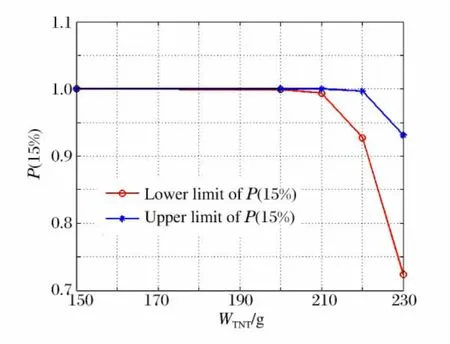
图7 TNT 当量与安全概率的关系图Fig.7 The relation between the security probability and TNT equivalence

本文在爆炸容器数值计算中考虑了主要计算参数的随机性，并通过Monte－Carlo方法获得了计算结果的随机样本，取代了以往单一的、确定性数值计算结果，能够更客观地反映真实的物理过程。应用统计分析方法对柱形容器爆炸后径向变形量的不确定性进行了定量描述，给出了在一定置信度下容器安全概率的区间估计。

［1］ 朱文辉，薛鸿陆，韩钧万，等.爆炸容器动力学研究进展评述［J］.力学进展，1996，26（1）：68－78.Zhu Wen－hui，Xue Hong－lu，Han Jun－wan，et al.The research advances in the dynamics of explosive chambers［J］.Advance in Mechanics，1996，26（1）：68－78.

［2］ 胡八一，柏劲松，刘大敏，等.爆炸容器的工程设计方法及应用［J］.压力容器，2000，17（2）：39－41.Hu Ba－yi，Bai Jing－song，Liu Da－min，et al.The engineering design method of explosion containment vessels and its application［J］.Pressure Vessel Technology，2000，17（2）：39－41.

［3］ 王定贤，胡昊，王万鹏，等.动力系数法在爆炸容器设计中的应用［J］.四川兵工学报，2011，32（4）：24－26.Wang Ding－xian，Hu Hao，Wang Wan－peng，et al.Application of the dynamical coefficient method in explosion vessel design［J］.Journal of Sichuan Ordnance，2011，32（4）：24－26.

［4］ 胡永乐，喻名德，崔云霄.爆炸容器塑性失稳和变形吸能［J］.兵工学报，2009，30增刊2：28－32.Hu Yong－le，Yu Ming－de，Cui Yun－xiao.Plastic instabilities and deformation energy absorption of explosion containment vessels［J］.Acta Armamentarii，2009，30suppl 2：28－32.

［5］ 陈国华，戴树和.概率安全评定方法的计算程序及其工程应用［J］.南京航空航天大学学报，1999，31（3）：346－350.Chen Guo－hua，Dai Shu－he.Calculating procedure of probability safety assessment method and its engineering application［J］.Journal of Nanjing University of Aeronautics ＆Astronautics，1999，31（3）：346－350.

［6］ 赵建平.压力容器概率安全评定技术进展［J］.化工设备与管道，2001，38（2）：17－19.Zhao Jian－ping.Survey of probabilistic safety assessment technology for pressure vessels［J］.Process Equipment ＆Piping，2001，38（2）：17－19.

［7］ 浦锡锋，王仲琦，白春华，等.用于爆炸流场与结构间相互作用分析的Euler－Lagrange耦合模拟技术［J］.爆炸与冲击，2011，31（1）：6－10.Pu Xi－feng，Wang Zhong－qi，Bai Chun－hua，et al.An Euler－Lagrange coupling method for numerical simulation of explosion－structure interaction［J］.Explosion and Shock Waves，2011，31（1）：6－10.

［8］ 吴翊，李永乐，胡庆军.应用数理统计［M］.长沙：国防科技大学出版社，2005：112－120.

［9］ 刘钰，韩峰，王玉恒，等.一种基于密度核估计的最大熵方法［J］.工程数学学报，2011，28（3）：285－292.Liu Yu，Han Feng，Wang Yu－heng，et al.A new maximum entropy method based on kernel density estimate［J］.Chinese Journal of Engineering Mathematics，2011，28（3）：285－292.

［10］ Casella G，Berger R L.Statistical inference［M］.Beijing：China Machine Press，2010：417－427.

［11］ 韩峰，王建国，乔登江.对数正态分布场合下产品加固性能的Bayes评估方法［J］.应用概率统计，2009，25（4）：433－440.Han Feng，Wang Jian－guo，Qiao Deng－jiang.Bayesian assessment for product’s radiation hardening performance under lognormal distribution［J］.Chinese Journal of Applied Probability and Statistics，2009，25（4）：433－440.

［12］ 袁亚湘，孙文瑜.最优化理论与方法［M］.北京：科学出版社，2001：373－391.