n+232Th核反应光学模型势的计算

王晓攀 陈金根 蔡翔舟 胡继峰

1（中国科学院上海应用物理研究所嘉定园区 上海 201800）2（中国科学院大学 北京 100049）

n+232Th核反应光学模型势的计算

王晓攀1,2陈金根1蔡翔舟1胡继峰1

1（中国科学院上海应用物理研究所嘉定园区 上海 201800）
2（中国科学院大学 北京 100049）

利用光学模型、宽度涨落修正的Hauser-Feshbach理论对中子入射232Th核反应进行了研究。以总截面、去弹截面以及弹性散射角分布的实验数据为依据，得到了n+232Th核反应在0.1–20 MeV能量区域的一套中子光学模型势参数，并以此计算了该反应的总截面、弹性散射截面、去弹截面和弹性角分布截面。理论计算结果与实验数据符合较好。

中子入射232Th核反应，光学模型，角分布，核模型理论计算

“未来先进核裂变能——钍基熔盐堆”是中国科学院首批启动实施的战略性先导科技专项，目标是研发第四代裂变反应堆核能系统——钍基熔盐堆核能系统。钍铀燃料循环可以将自然界中的可裂变核素232Th转化为易裂变核素233U，以缓解核燃料资源供应紧张。此项目需要大量核反应的微观数据，特别是中子入射重要裂变核反应数据。钍作为钍铀燃料循环中的基础核素，其全套的评价中子核数据，如常用截面核数据、角分布核数据对核工程设计的精准性起着至关重要的作用。

IAEA在2002年成立了钍铀燃料循环相关评价核数据的国际合作项目(Th-U CRP[1])，并评价了新版的232Th全套中子数据，收录在ENDF/B-VII.0，中国核数据中心和日本核数据中心也分别在2009年和2010年重新评价了232Th的核反应数据，在CENDL-3.1和JENDL-4.0库中发布。在应用于钍铀燃料循环核工程设计及技术积累角度需要对其进行重新计算和评价。

为了提高核反应微观全套核数据评价的质量，首先需要给出一套合适的光学势参数。因为光学模型势参数决定了去弹截面，影响了其他反应道的截面大小。一组好的光学势的重要特征之一就是即使在没有实验数据存在的能区，也可以计算出可靠的反应截面和弹性散射角分布[2]。本文利用光学模型、宽度涨落修正的Hauser-Feshbach理论对中子入射232Th核反应进行了研究。

本工作使用APMN程序[3], 得到了n+232Th核反应在0.1–20 MeV能量区域的一套最佳中子光学模型势参数。这组光学势参数优于普适光学势参数。利用这组中子光学势参数计算了该反应的总截面、弹性散射截面、去弹截面和弹性角分布截面。

1 光学模型理论及参数调整

光学模型是核反应的重要理论[3,4]，可给出反应总截面、吸收截面、弹性散射截面和弹性散射角分布。吸收的部分或者发生直接反应，或者进入靶核形成复合核。核反应过程的不同阶段有不同的特点，需要用不同的模型机制来描写，但吸收截面、反应截面的大小由光学模型完全确定下来，所以光学模型直接决定了其它机制的贡献，以及各种反应道截面的总和，截面之间关系可用下式表示：

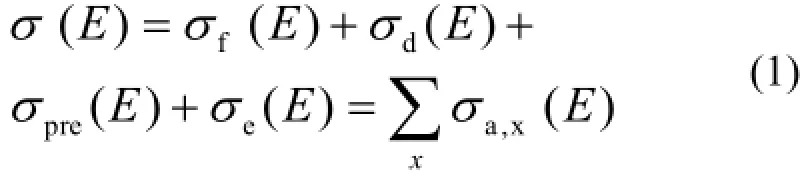
式中，σ为总吸收截面；fσ为裂变截面，dσ为直接反应截面；preσ为预平衡衰变截面；eσ为平衡衰变截面；a,xσ为各类吸收截面。

由此可见，吸收截面决定裂变截面和发射其它粒子截面的大小。光学模型的核心通过数值解定态薛定谔方程计算出总截面、弹性角分布、去弹截面。

式中，()Ur为中子和靶核体系的光学势。本工作中实际数据计算选用相对成熟的唯象光学势，唯象光学势中最常用的是Woods-Saxon势。它的一般形式如下(能量单位MeV，长度单位fm)：

上式各项分别为：库伦势、实部势、虚部势(体吸收、面吸收)、自旋轨道藕合势。

上式为库伦势，其中根据实验数据可调整的参数为rc，对中子反应库伦势为零。

能量相关的中心实部势的表达式为：

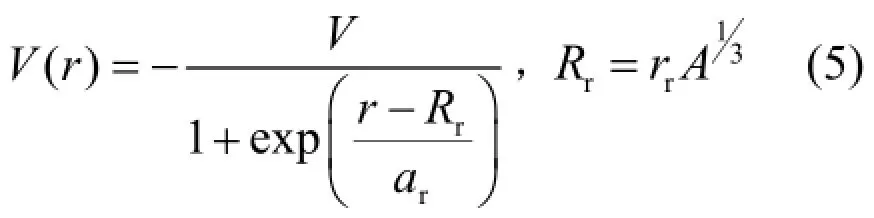
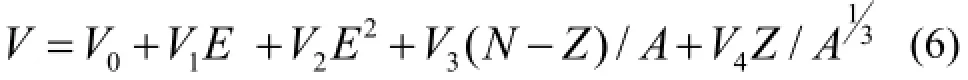
根据实验数据可调整的参数为：V1、V2、V3、V4、ar、rr。面吸收虚部势形式为：

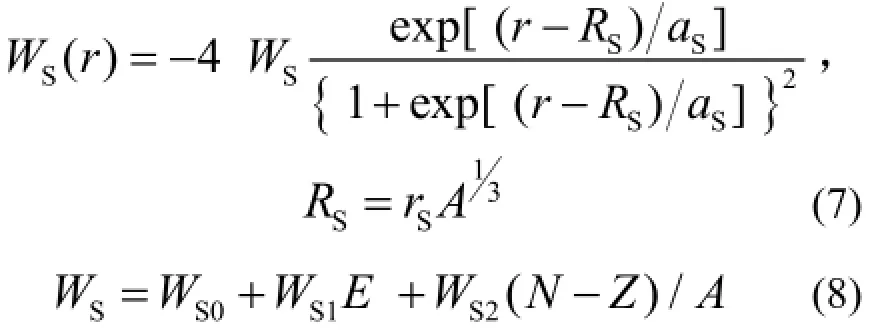
体吸收虚部势形式为：

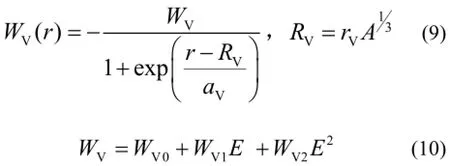
式中，VSO(r)和WSO(r)分别为自旋-轨道耦合实部势和虚部势，它们的表达式为：

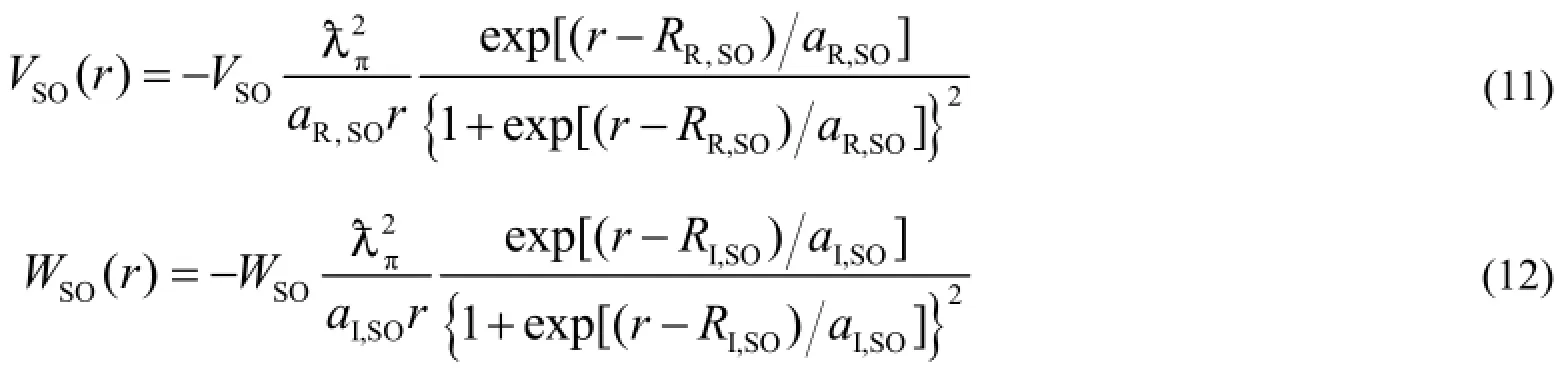
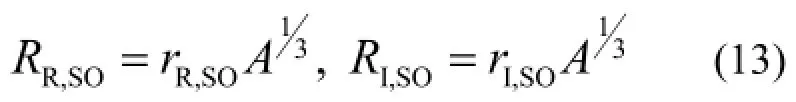
本文使用APMN程序寻找20 MeV以下入射中子的最佳光学势参数，主要是以总截面、去弹截面、弹性角分布实验数据为依据，经APMN程序得到调节，以最好的符合实验数据。APMN程序拟合实验数据以寻求最佳光学势参数的基本原理是变步长最速下降法。由参数初值先得到一个表示计算结果与实验数据偏差的量χ2，然后利用最速下降法改变光学势参数并计算新的χ2值，若某一组光学势参数使χ2最小[2,3]，即认为此组光学势参数为最佳参数。定义如下：式中，Nu为考虑的核子数目；Wi为第i个核子的权重；Wi,tot、Wi,ne、Wi,el分别为第i个核子的总截面权重、去弹散射截面权重及核子弹性散射角分布的权重，Wi,tot=0是对于带电粒子入射的反应道；Ni,tot、Ni,ne、Ni,el分别为第i个核子总截面实验数据的能点数目、去弹散射截面的能点数目和弹性散射角分布的能点数目；Ki,j,el为第i个核子第j个能点角分布实验数据的角度个数；T、E分别代表理论值和实验值；σI,tot(j)、σI,ne(j)为第i个核子、第j个入射能点的总截面和去弹散射截面；σi,j,el(θι,j,k)为第i个核子、第j个能点、第k个出射角度的弹性散射角分布；σ△为相应数据的实验数据误差。式(14)–(18)给出的χ2值被认为是N个可调光学势参数的函数。

工作中首先对n+232Th反应所能收集到的实验数据进行了分析评价，然后以实验数据为依据，使用APMN程序计算出总截面、弹性散射截面、去弹弹射截面，并通过计算结果和实验数据的比较来确定一套合理的光学势参数。初始值我们使用普适光参数[4]，经过适当的人为控制得到最佳中子入射232Th光学势参数见表1。

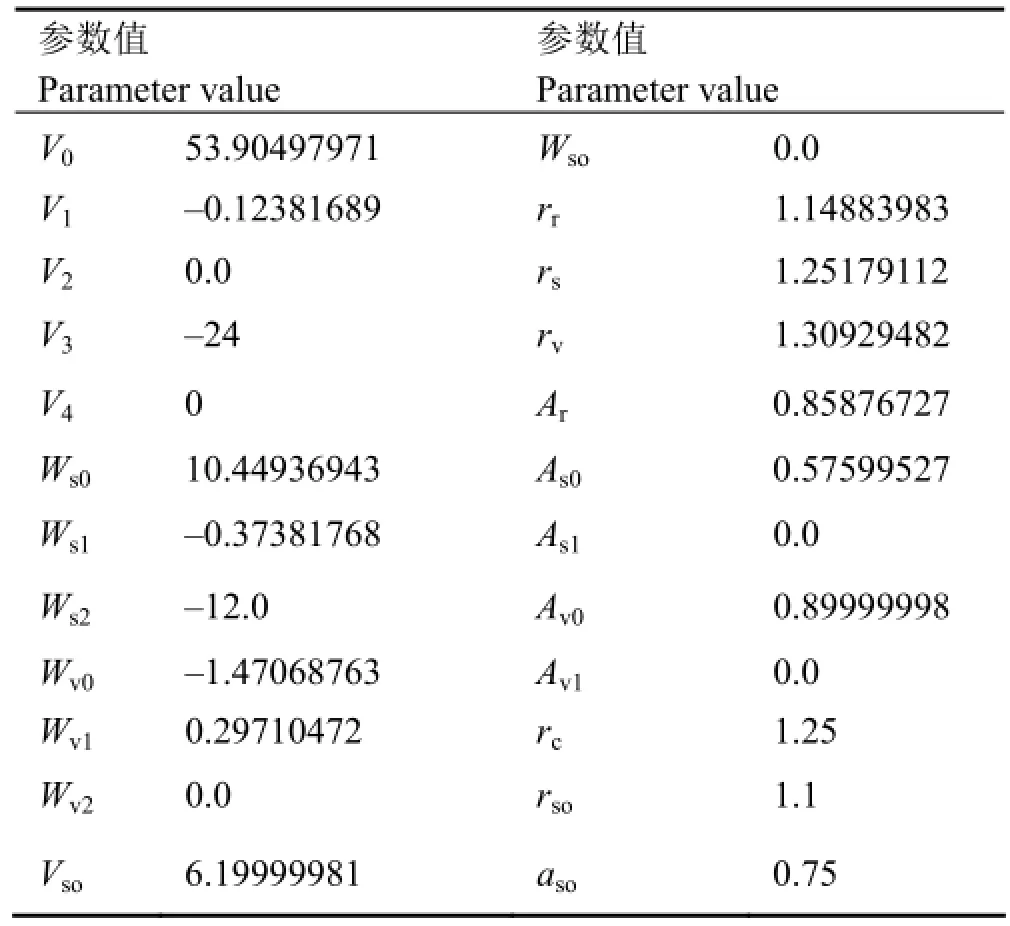
表1 n+232Th最佳光学势参数Table1 Neutron optical potential parameters for n+232Th.

2 计算结果和实验数据的比较和分析

图1为232Th(n,tot)反应道的理论计算截面与实验数据的比较。入射中子能量为0.1–20 MeV的总截面实验数据经筛选共有23组，数据分歧不大，总体上看得到的光学势参数与实验数据符合较好[5–8]。

图2为232Th(n,el)反应道的计算结果和实验数据的比较。弹性散射截面的实验数据仅10家且测量的能点很少。在1–2 MeV之间理论曲线低于实验数据，但从总截面及图3的去弹截面看，如果将弹性截面上调1.5 b左右，则去弹截面将明显偏小。同时，弹性散射截面是弹性角分布的积分，从后边的弹性角分布符合情况看，理论给出的曲线是合理的。

图1 调参前后总截面计算结果和实验数据的比较Fig.1 Calculated neutron total cross section before and after adjusting parameters compared with experimental data.

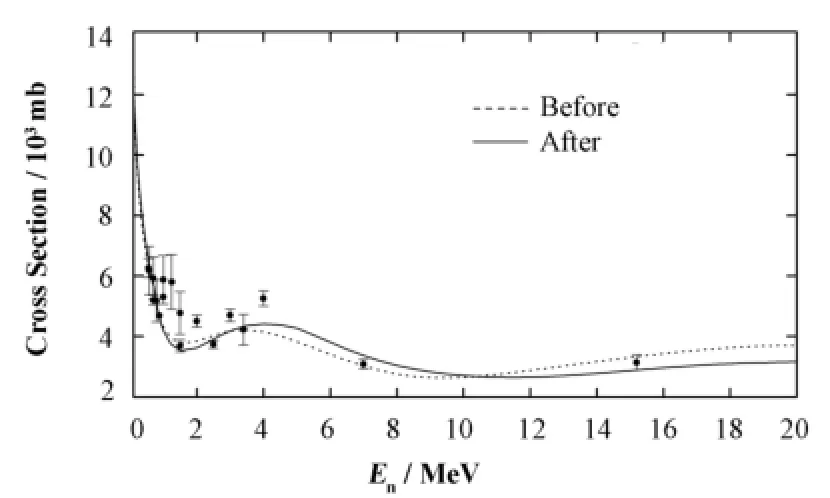
图2 调参前后弹性截面的计算结果和实验数据的比较Fig.2 Calculated neutron elastic cross section before and after adjusting parameters compared with experimental data.

图3 为调参前后232Th(n,non)反应道的计算结果和实验数据的比较。去弹散射截面实验数据都比较少，我们只找到2家共4个能点的实验数据[9,10]。从其他相似的反应趋势及数值大小看我们的结果合理。

图3 调参前后去弹截面的计算结果和实验数据的比较Fig.3 Calculated neutron nonelastic cross section before and after adjusting parameters compared with experimental data.

图4 为232Th弹性散射角分布的计算结果，选择了能区范围内有实验数据的14个入射能点，给出了计算结果和实验数据的比较。图中理论值和实验值从上到下依次乘以10–3、10–2、10–1、100、101、102、103。由图可见，大部分能点实验数据和理论计算结果符合很好，在0.8、2.0、5、15.2 MeV处某些角度的角分布理论计算结果和实验数据没有完全符合，但实验数据和理论计算结果整体趋势是一致的。0.8 MeV的理论值明显比实验数据[11]偏高，但从0.7 MeV的曲线及实验数据符合情况来看，0.8 MeV的实验数据可能偏高。

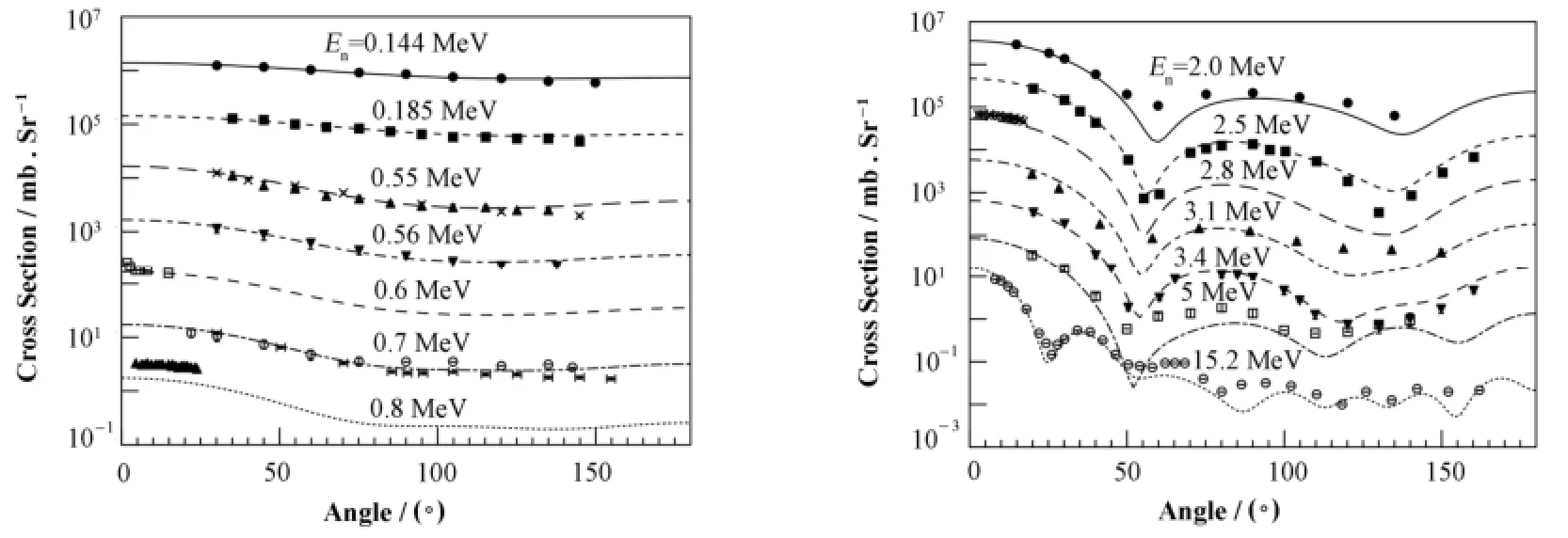
图4 弹性散射角分布的计算结果和实验数据的比较Fig.4 Calculated neutron elastic scattering angular distribution compared with experimental data.

对于不同入射能量的中子，反应截面随着出射粒子角度的分布表现出不同的趋势。在入射能量较低的能区，角分布比较平缓，趋于直线，出射粒子角度呈现各向同性特征。随着入射粒子能量的增大，角分布曲线出现周期性波动，形成波谷和波峰，且能量越高，波的幅度越大，这说明大角度的散射减小。而这种波动则是由于核结构效应例如核振动引起的。

3 结语

利用程序APMN结合相关实验数据给出了232Th元素中子核反应入射中子在0.1–20 MeV能区的一组最佳光学模型势参数。利用这组参数计算了总截面、去弹截面、弹性散射截面和弹性散射角分布。结果表明，得到的理论计算结果和实验数据符合较好，这组参数可以用在直接非弹、预平衡发射及平衡发射计算中。在此基础上可以进一步利用扭曲波波恩近似、激子模型、蒸发模型等理论计算出包括出射粒子能谱、双微分截面等重要数据的全套反应数据。

1 Schillebeeckx P, Trkov A. Evaluated nuclear data for Th-U fuel cycle[R]. International Nuclear Data Committee, Vienna, Austria, 2004

2 Han Y L, Xu Y L, Liang H Y, et al. Global phenomenological optical model potential for nucleonactinide reactions at energies up to 300 MeV[J]. Physical Review C, 2010, 81: 0246461–02464611

3 Shen Q B. User manual of APMN06 code[M]. Beijing: China Nuclear Data Center, 2006: 1–32

4 Becchetti F D, Greelees G W. Nucleon-nucleus optical-model potential, A＞40, E＞50 MeV[J]. Physical Review, 1969, 182(Issue 4): 1190–1209

5 Poenitz W P, Whalen J F, Smith A B. Total neutron cross sections for heavy nuclei[J]. Nuclear Science and Engineering, 1981, 78: 333–345

6 Iwasaki T, Baba M, Hattori K, et al. Measurement of neutron total cross section for Th-232[R]. Japanese report to NEANDC, No.83/U, 5-21, 1982

7 Foster Jr D G, Glasgow D W. Neutron total cross section 2.5–15 MeV. I. Experimental[J]. Physical Review C, 1971, 3: 576–588

8 Abfalterer W P, Batenman F B, Dietrich F S, et al. Measurement of neutron total cross sections up to 560 MeV[J]. Physical Review C, 2001, 63: 044608–044623

9 Batchelor R, Gilboy W B, Towle J H. Neutron interactions with U-238 and Th-232 in the energy region 1.6 MeV to 7 MeV[J]. Nuclear Physics,1965, 65: 236–251

10 MC Taggart M H, Goodfellow H. Measurements at 14 MeV neutron energy of the N, 2N cross section of beryllium and the N,3N cross section of Thorium[J]. Nuclear Energy Part A+B (Reactor Science Technology), 1963, 17: 437–452

11 Aleksandrov Ju A, Anikin G V, Soldatov A S. Small-angle scattering of 0.8 MeV and 2.8 MeV neutrons[J]. Zhurnal Eksperimental’ noi Teoret. Fiziki, 1961, 40(Issue 6): 1878–1891

CLCTL32

Calculation of optical model potential for n+232Th reaction

WANG Xiaopan1,2CHEN Jingen1CAI Xiangzhou1HU Jifeng1

1(Shanghai Institute of Applied Physics,Chinese Academy of Sciences,Jiading Campus,Shanghai 201800,China)
2(University of Chinese Academy of Sciences,Beijing 100049,China)

Background:Accurate nuclear data are needed for the development of molten salt reactors which use thorium as nuclear fuel. Purpose: We attempt to get an optimum set of optical potential parameters for232Th with the incident neutron energy from 0.1 MeV to 20 MeV. Methods: APMN code which based on optical theory and Hauser-Feshbach theory with width fluctuation correction was used. Steepest descent method was adopted when the code seeks the optimum optical parameters automatically. Results: The comparison between the experimental data and the calculation results before and after adjusting the optical parameters shows that the calculation results after adjusting are in better agreement with the experimental data. This set of parameters could be used for nuclear data calculation. Conclusions: Based on the results it could provide a believable set of optical parameters for the neutron data evaluation.

n+232Th reaction , Optical model, Angular distribution, Nuclear model theory calculation

TL32

10.11889/j.0253-3219.2013.hjs.36.060603

中国科学院战略性先导科技专项资助项目(XDA02010200)

王晓攀，女，1986年出生，2013年于上海应用物理研究所获硕士学位，从事反应堆核数据计算

2013-03-11，

2013-03-25