非均匀风场与急流强迫的水体涡旋动力特征模拟

王坚红，冯呈呈，苗春生，李洪利，耿珊珊

(1.南京信息工程大学，江苏 南京210044;2.国家海洋信息中心，天津300171)

0 引言

涡旋运动作为地球流体运动中的重要组成部分，广泛的存在于大气、海洋、湖泊等各种流体之中。涡旋不仅影响流体的运动状态，还承担流体中的物质输送及能量传输。因此，涡旋研究成为海洋、湖泊及大气动力学研究的重点。常见的大气涡旋有:积云对流单体，龙卷风，中尺度涡旋系统，中尺度对流系统，温带气旋，热带气旋，极地低压和副高等。常见的海洋涡旋有中尺度涡旋，具有气旋式或反气旋式环流特征(Robinson，1984)，以及海流绕过海岛后产生的障碍扰流脱落涡旋等(刘泽等，2009)。类似的情况也发生在湖水中，产生不同尺度涡旋。涡旋的生成、维持与消亡，是大气环流以及海洋环流特征时空演变的重要组成部分(袁耀初和管秉贤，2007;程旭华和齐义泉，2008;赵杰，2010)。影响海洋涡旋生成的环境因子有急流两侧的切变流(陈红霞，2008)、障碍扰流脱落涡旋(管秉贤和袁耀初，2006)、地形强迫涡旋(陈更新，2010)、海面非均匀风场的强迫(王桂华，2004)、地转偏向力的强迫(贺志刚等，2001;徐晓华等，2010)等。大气中涡旋的生成也受类似影响因子作用，如急流两侧的切变流(李建辉等，1985;尹东屏等，2007)、障碍扰流脱落涡旋(Colle，2004)、地形强迫涡旋(周玉淑和李柏，2010)、热力强迫涡旋(陈淑敏等，2008;白莉娜等，2010)、地转偏向力强迫(桂海林等，2010)等。显然大气动力与热力过程、海洋动力热力过程、海气相互作用以及地球旋转效应造成了海洋、湖泊与大气中涡旋的生成以及复杂多样的结构。

海洋、海湾、湖泊等大形水体以大气为上边界，受大气风场风应力的直接强迫;同时海湾、湖盆具有固体环境边界，流动受边界形态强迫引导;在近岸还有径流持续输入，造成水体内部大尺度急流运动。因此海洋、海湾、湖泊涡旋的形成具有多种影响因子，其中动力强迫起着重要的作用。本文重点考虑海气界面风应力和水体内强切变急流的动力强迫以及多因子综合效应，分析它们对近海、海湾、湖泊类水体涡旋生成及结构特征的影响，并定量化地讨论涡旋切变能量转换作用及对涡旋特征的影响。

1 模拟设计与分析方法

1.1 涡旋形成的主要动力因子

我国南海海域作为西太平洋最大的半封闭边缘海，地理环境特殊。冬、夏季海面受到相互反向的冬季风和夏季风的强迫以及其他因素影响，上层水平环流具有复杂形态特征，并呈现多涡的特点。运用SODA(Simple Ocean Data Assimilation)海洋资料，经统计得到南海地区10 a平均环流场，如图1所示，南海海域平均环流场呈现多涡结构，并有3条显著的急流，东侧为自南向北，西侧为自北向南，东南角为自东向西。急流右侧为负涡旋，左侧为正涡旋。

图1显示在台湾岛东侧的黑潮以及黑潮急流右侧的流动侧向切变造成的反气旋式涡旋。在海南岛南侧与越南东部，由于地形结构，形成的反气旋式涡旋。在图1的右下部分，由于菲律宾诸岛的阻挡，来自西太平洋的海流穿越诸岛后在菲律宾群岛西侧形成两个气旋式涡旋。在南海南部印度尼西亚西北和马来西亚的东部，海流受地形影响，形成四个不同尺度的涡旋，并组成鞍形流场。Wang et al.(2005)对卫星资料QuikSCAT南海海面高度场季节分析的结果指出，南海夏季海面大尺度环流中正负偶极形涡旋的分布，与南海夏季风急流位置相匹配，而南海冬季风与自西太平洋经菲律宾进入南海的海流走向一致，风应力对绕岛脱落涡旋的形成有增强作用。Wang et al.(2012)给出美国阿拉斯加高频雷达对局地Prince William Sound海湾海面环流的观测分析显示，该海湾由大陆与岛屿环绕，海面近似圆形，有径流及潮汐影响，形成尺度相当于该海湾的独立气旋式环流，水平尺度约80～90 km。在上述的各实例中海气相互作用的非均匀风场、急流两侧的流速切变、环境地形的强迫引导等都是涡旋形成的主要动力因子。其中，地转偏向力作用也很显著，同样流速，高纬度的Prince William Sound海湾地转偏向力大于低纬南海海域，造成流动在高纬向右偏更显著，因此Prince William Sound海湾中，北侧的流动以及河口径流偏西，南侧的流动偏东，于是有利于该海湾中形成逆时针的大尺度环流。在南海，季风风应力的作用更强，海面环流与涡旋受非均匀风力场的强迫更显著，环流呈现多涡旋复杂状态。

图1 南海海域1995—2004年10 a平均环流 a.环流分布;b.平均流速分布(单位:cm/s)Fig.1 Average circulation in the South China Sea from 1995 to 2004 a.circulation distribution;b.average velocity distribution(units:cm/s)

1.2 模拟设计

为分析各项动力影响因子对水体涡旋形成及其形态特征的作用，包括各因子独立作用、叠加作用、以及不同强度的量化效果等，对水体涡旋生成过程以及结构特征进行了系列数值模拟。采用圆形边界水域，取30°N。关于水气界面的风场特征，取非均匀非定常的单急流和双急流的两种典型风场。水体中高层单侧增加径流，并具有不同的强度。模拟试验的分组设计如表1所示。试验1、2、3只考虑单因子影响，试验4、5为非均匀风场与急流的综合因子影响。其中，A型风场为急流在中部，沿急流轴速度非均匀;B型风场为两条强风带，南侧边界强风带较北部急流短;水体内径流的出入口在实验中均设计位于水域右侧。

表1 模拟试验设计Table 1 Simulation experiment design

设计的两种风场分布特征如图2所示。图2a为A型风场的空间分布形势，方向为自西向东，中部为急流，沿急流轴速度非均匀;图2b为B型风场的强弱分布形势，方向为自东向西，两侧风速强，中部风速弱，强风速轴分布长度不等，沿风速轴风速分布非均匀。风场设计类型源于实验室模拟的非均匀风场的纪录。

水体中径流空间分布如图3所示。图3a为模式水平三角网格，箭头指示径流入口与出口位置;垂直分布如图3b所示，径流主体位于水体上部，最大流速在垂直第7层。径流流量分别取为100、500、1 000、1 500 m3/s。

1.3 FVCOM数值模式

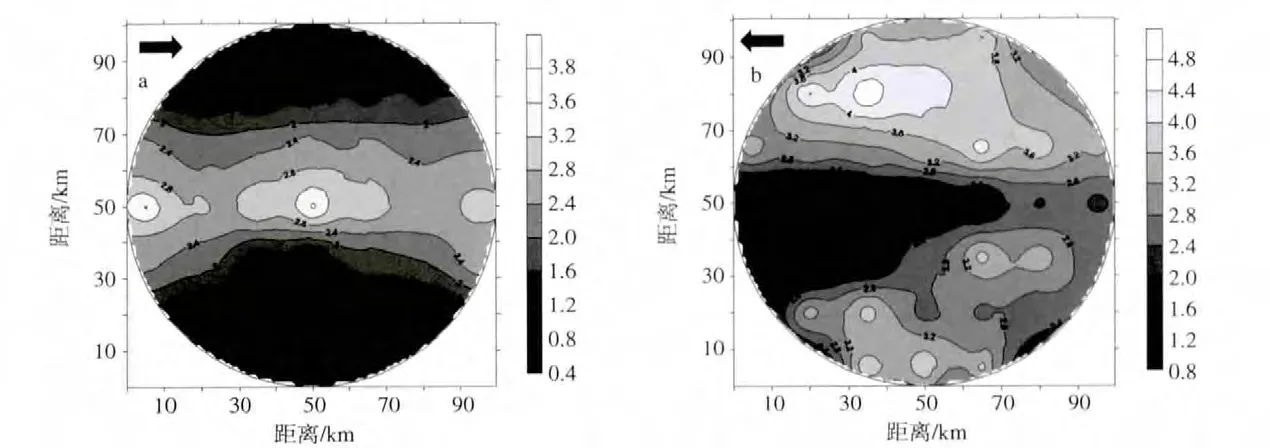
图2 非均匀风场分布特征 (单位:m/s;图中矢量标示风向;浅色表示速度大值) a.A型风场;b.B型风场Fig.2 Non-uniform wind field distribution(units:m/s;vector indicates wind direction;light color denotes large speed)

图3 网格设置与水体径流分布特征示意 a.水平分布;b.垂直分布Fig.3 The grid setting and the water jet current distribution a.horizontal distribution;b.vertical distribution

本文水体涡旋动力影响模拟采用FVCOM(Finite Volume Coast and Ocean Model)海洋数值模式(陈长胜，2003;Chen and Liu，2003;Chen et al.，2006)。为基于三角形网格，采用有限体积方法，三维(3D)原始方程组局域海洋数值模式。FVCOM模式综合了有限差分法和有限体积法，既可以精确地拟合复杂海岸线，又可对局部网格进行加密，计算速度快。模式采用了体积通量的积分方法来求解流体动力学原始方程组，保证了在单个网格和整体计算区域上都能同时满足动量、能量和质量的守恒，解决了海洋数值计算中最关键的问题。近年来，该模式被广泛地应用于近岸海洋及湖泊的多种问题研究中(冯兴如等，2010;曹振东和娄安刚，2011;王坚红等，2011;赵巧华等，2011)。

模型的控制方程采用笛卡尔坐标系下的原始控制方程组，包括动量方程、连续方程、温度方程、盐度方程和密度方程:

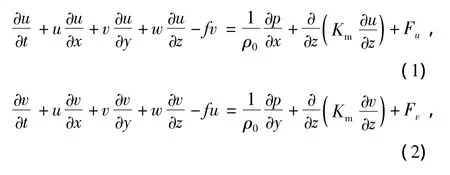
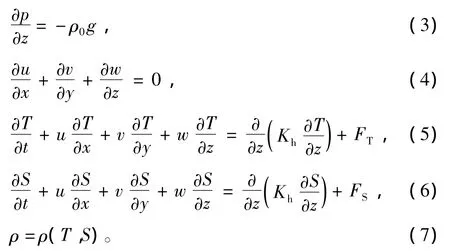
其中:x，y，z为笛卡尔坐标系下的三维坐标，分别为东西方向、南北方向以及垂直方向的坐标;u，v分别为水流水平方向的东分量速度和北分量速度;w为垂向速度;g为重力加速度;t为时间;ρ0为平均密度;S为水体盐度;T为水温;p为气压;f为科氏参数;Km为垂向涡动粘性系数;Kh为垂向热量涡动扩散系数;Fu和Fv为x方向和y方向水平动量扩散系数;FT与FS为水平温度与盐度扩散系数。

模拟研究中重点考虑动力强迫，关闭盐度模块，水温取为定常值。参考海湾、湖泊、近岸浅海海域的地理情况，取理想化圆形场区域，直径设为100 000 m，深度取为5 m。时间积分步长为1 s，内外膜比值取5，总时间长度设为48 h(2 d，模式运行6 h达到稳定)。积分期间每0.5 h输出一次结果。模拟区域的纬度取30°N。侧边界设为固体边界，相当于有地形阻挡的水体区域。垂直层次均匀10层。使用湍流闭合模块(GOTM)中的k-ε湍流模型。使用SMS软件生成圆形区域的三角网格(如图3a所示)，其中，节点8 337个，单元格16 372个。

1.4 涡旋动力特征分析方法

为定量描述水体涡旋的强度与形态特征，对环流场进行流函数与势函数分析。通过克里格插值方案对三角网格输出进行直角坐标系转换，进而对流动速度场求涡度散度，再由泊松方程迭代获得流函数ψ及速度势φ的定量空间分布。

流函数主要给出流动的无辐散运动成分及涡旋运动的特征与强度，根据已有的计算分析(谢安和白人海，1995;朱宗申等，2009)，在北半球正值对应反气旋式流动，负值为气旋式流动;速度势函数主要定量反映流体的无旋转运动成分，体现流体的辐散、辐合性质。正值为辐散，负值为辐合。

由于是区域迭代求解，因此需要对运算的收敛性及求解效果进行检验。主要方法为用迭代求解获得的流函数与势函数反算格点上u、v，重建全流场。然后计算泊松方程迭代前后两流场的空间相关，当重建的流场与原流场分布型式相关度高，误差量小时，说明求解的流函数与势函数的结果是收敛的，求解效果可信度高(离爱兵等，2012)。重建场与原始场之间的相关性(陈建萍，2003)定义如下:

设定义在区域 Σ =(γ1，γ2)× (λ1，λ2)上两个平面向量 V1(γ，λ，t)和 V2(γ，λ，t)，它们的形态相关度为:

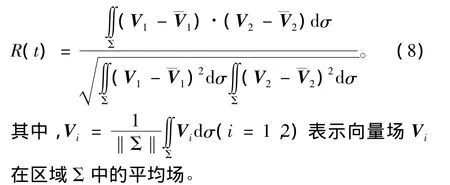
经过验证，本文得到的各重建流场与原始流场各时刻及各层的场相关系数均达到97%以上，因而本研究求解的流函数和势函数是收敛的，对环流及涡旋的特征定量描述是合理的。

2 非均匀风场驱动的涡旋动力特征

2.1 非均匀A型风场驱动的涡旋动力特征

在A型风场(图2a)风应力的作用下，FVCOM数值模拟获得的水动力涡旋环流如图4所示。图4给出了积分24 h与48 h的表层流场和底层流场形态。

图4显示在A型风场风应力驱动下，水体环流也呈现中部东西向大流速，南北两侧切变形成正逆向涡旋，底层的涡旋环流与表层基本一致，随着时间演变，涡旋环流基本稳定。流动的强度随深度减小，表层流速大于底层流速，表层急流最大流速约为11.5 cm/s，底层急流最大流速约6.5 cm/s，前者约为后者的1.8倍;流场对风场的响应随时间增强，然后稳定，表层与底层趋势一致。为了对全场环流更直观定量化地了解，认识非均匀风场驱动的水体涡旋强度的时空特征，采用流函数与势函数描述，如图5所示。

图5显示，流场对风场响应显著，流场中部流函数的等值线密集带为急流区，急流北侧为正涡旋，涡旋中心对应流函数的负值中心，在急流南侧为负涡旋，涡旋中心对应流函数的正值中心。并且，在急流南侧的涡旋强度较北侧的大，流函数正值中心强度均大于负值中心的强度，强度差可达涡旋强度三分之一。这应该与北半球指向流速右侧的科氏力作用有关。科氏力改变流动方向，有利于北半球流动的右偏，因此更利于负涡旋的活动增强，而对正涡旋活动则有一定减弱。

流函数场还显示由表层至底层强度逐渐减小，等值线也转为稀疏，但流型是近似的。在急流两侧，随着积分时间增加，涡旋强度有一些增强，表层流函数负值中心由 －900 s－1增为 －1 100 s－1，正值中心由 1 300 s－1增为 1 500 s－1，底层负值中心由 － 500 s－1增强到 －700 s－1，正值中心由700 s－1增加到900 s－1。势函数场的正负中心指示辐合辐散中心，负值为辐合，正值为辐散。由图5还可见，上(实线)下(虚线)层对应相反的散度中心，表层辐合中心对应底层辐散中心，表层辐散中心对应底层辐合中心，因此在势函数中心区域有垂直运动。在表层，沿急流方向，在急流上游为正势函数，南北有两个势函数正值中心，即存在辐散运动，流动加速向急流区汇合;在急流下游为负的势函数区，南北两侧分别有负的势函数中心，即存在辐合运动。势函数中心在急流北侧较强。在急流北侧，24 h表层与底层的大值中心分别为160、－60 s－1，48 h 为 160、－40 s－1。在急流南侧相对较弱，24 h表层与底层的大值中心分别为 －120、30 s－1，48 h 为 －80、40 s－1。显示急流北侧有较强的辐合辐散有利于整层通过垂直运动进行质量输运与交换。由于急流北侧是正涡旋环流，因此显示正涡旋区较负涡旋区具有更强的辐合辐散，这使得垂直上升运动强于急流南侧负涡度区的下沉运动。随着时间演变，急流北侧气旋式环流的辐合辐散程度略有增强，而急流南侧反气旋式环流的辐散辐合程度有所减弱。

图4 A型风场驱动的水体涡旋环流(单位:cm/s;色标指示流速大小) a.积分24 h表层环流;b.积分24 h底层环流;c.积分48 h表层环流;d.积分48 h底层环流Fig.4 Water vortex circulation forced by pattern A wind field(units:cm/s;color indicates flow speed) a.surface circulation in 24 h;b.bottom circulation in 24 h;c.surface circulation in 48 h;d.bottom circulation in 48 h

涡旋环流的表层水位特征如图6所示，图6a为响应A型风场的气旋与反气旋涡旋表面高度场。

由图6a可见，A型风场造成的气旋式涡旋对应着负水位(下凹的水位)区，中心值约－0.09 m，反气旋式涡旋对应着正水位(上凸的水位)区，中心值约0.09 m。沿y=75 000 m的垂直剖面显示，气旋式涡旋东侧向北的流动对应着宽的倾斜表面，为倾斜流和梯度流，气旋式涡旋中心(x=50 000 m)位于低水位处。y=35 000 m的垂直剖面显示，反气旋西侧向南的流动对应着宽的倾斜表面，为倾斜和梯度流，反气旋式涡旋中心(x=50 000 m)位于高水位处。自西向东的急流与密集的高度梯度对应，显示梯度流的强劲。

2.2 非均匀B型风场驱动的涡旋动力特征

具有两条自西向东强风带的B型风场驱动的水体环流如图7所示，给出了积分48 h的水体水平涡旋流场。上下层涡旋环流形势基本类似，并且正涡旋的尺度显著大于南部的负涡旋，流函数给出了定量的指示。

由图7a1、7b1流动矢量场可见，水体表层流场有两条同向急流，一条在南侧边界(自东向西)，较短偏弱。另一条对应风场强急流，位于水域北部，自东向西，尺度较长。在两条急流之间的弱风区，受两侧急流流动驱动，自西向东，形成回流逆流，位于流场中部。因此两不等强度的急流间形成两个正反向涡旋。并在东南区域还形成一个小的气旋式涡旋，在这种风场形势驱动下，水域环流流场较为复杂，出现多个环流共存的现象。

与A型风场驱动的涡旋环流场类似，这种由界面风场驱动的水体涡旋上下层环流形态近似，均呈多涡型，上层环流强度强于下层。在积分稳定的48 h，表层最大流速约为13.1 cm/s。底层流速强度最大值6.8 cm/s，减弱近一半。

图5 A型风场驱动下表层(实线)和底层(虚线)的水体流函数(a，b;单位:s－1)与势函数(c，d;单位:s－1)分布 a.积分24 h的流函数;b.积分48 h的流函数;c.积分24 h的势函数;d.积分48 h的势函数Fig.5 (a，b)Water stream function(units:s－1)and(c，d)potential function(units:s－1)forced by pattern A wind(solid lines present surface elements;dash lines presenst bottom elements) a.stream function in 24 h;b.stream function in 48 h;c.potential function in 24 h;d.potential function in 48 h

图6 A型风场驱动出的水位分布(单位:m) a.表层;b.沿y=75 000 m的涡旋中心垂直剖面;c.沿y=35 000 m的涡旋中心垂直剖面Fig.6 Distribution of water level(units:m)driven by wind pattern A a.surface water level;b.vertical profiles along y=75 000 m at center of the vortex;c.vertical profile along y=35 000 m at center of the vortex

流函数场(图7a2、7b2)显示，与强而长的风场急流配合的水体气旋式涡旋尺度大、强度强，流函数中心值达到－1 900 s－1。与南侧边缘短尺度急流配合的反气旋式涡旋较弱，强度大致为700 s－1。东南部的小涡旋强度为－500 s－1。从表层向底层涡旋强度减弱，气旋式涡旋流函数值减弱约32%，反气旋减弱约29%，小涡旋的强度维持，但尺度缩小。势函数的分布(图7a3、7b3)显示，大而强的气旋式涡旋对应的是整层的辐合，反气旋涡旋对应的是表层辐合，底层辐散，小的气旋式涡旋对应的是表层辐散，底层辐合。因此对此三个涡旋区的垂直运动分别为强的上升运动、下沉运动及上升运动。

图7 B型风场驱动的积分48 h流场形势 a1.表层环流矢量场(单位:cm/s);a2.表层流函数场(单位:s－1);a3.表层势函数(单位:s－1);b1.底层环流矢量场(单位:cm/s);b2.底层流函数场(单位:s－1);b3.底层势函数(单位:s－1)Fig.7 Flow patterns forced by wind pattern B in 48 h a1.surface flow vector field(units:cm/s);a2.surface stream function field(units:s－1);a3.surface potential function field(units:s－1);b1.bottom flow vector field(units:cm/s);b2.bottom stream function field(units:s－1);b3.bottom potential function field(units:s－1)

3 急流驱动的涡旋动力特征

模拟区域中水体中急流的位置设置在圆形场的右侧，具体如图3所示。流量分别取为100、500、1 000及1 500 m3/s四个级别。在无风场仅有急流形势下，驱动出的水体涡旋流场的流函数与势函数分布如图8所示。

图8显示，急流自南向北通过模拟区域右侧，在入口区急流两侧的强切变造成急流右侧与边界间形成反气旋式涡旋(正流函数中心)。随着急流流量强度的增加，急流尺度增大，增宽，侧向切变增强，该涡旋随之增强增大，流函数值由800 s－1增强到2 500 s－1。在急流左侧，流场宽阔，形成的正涡旋(负流函数中心)尺度大，随着急流流量的增强，正涡旋范围扩展，流函数0线逐步向西移动，负中心由－800 s－1增强到 －2 000 s－1。在急流出口区，随着流量的增强，流量达1 000 m3/s时，生成了小的正涡旋。这样的多涡环流形与图1南海多年平均环流有相似。

对应的势函数场显示，急流入口区对应势函数正中心，即辐散区;急流出口区对应势函数负中心，即辐合区。辐合辐散的强度均随急流强度的增强而增大，这与急流增强、流速切变梯度增大，辐合辐散更为显著有直接关系。急流侧向切变增强，造成的切变涡度增大，辐合辐散的流动部分也加强。

此外在模拟区域中(图8g)，负涡旋的强度3 000 s－1绝对值显著大于正涡旋强度－2 000 s－1的绝对值，这与风应力场驱动的涡旋特征一样，与北半球地转偏向力有利于驱动负涡旋式运动的作用有关。

关于这两种涡旋即非均匀风场风应力驱动的涡旋与急流侧向切变形成的涡旋的区别，通过对涡旋垂直结构进行比较，选取图6a中风应力生成的涡旋，沿中心y=75 000 m剖面，此时涡旋表面最大流速0.117 6 m/s;另选取图8g中水体急流生成的涡旋，沿中心y=30 000 m剖面，此时涡旋表面最大流速7.184 m/s。两涡旋垂直剖面如图9所示。

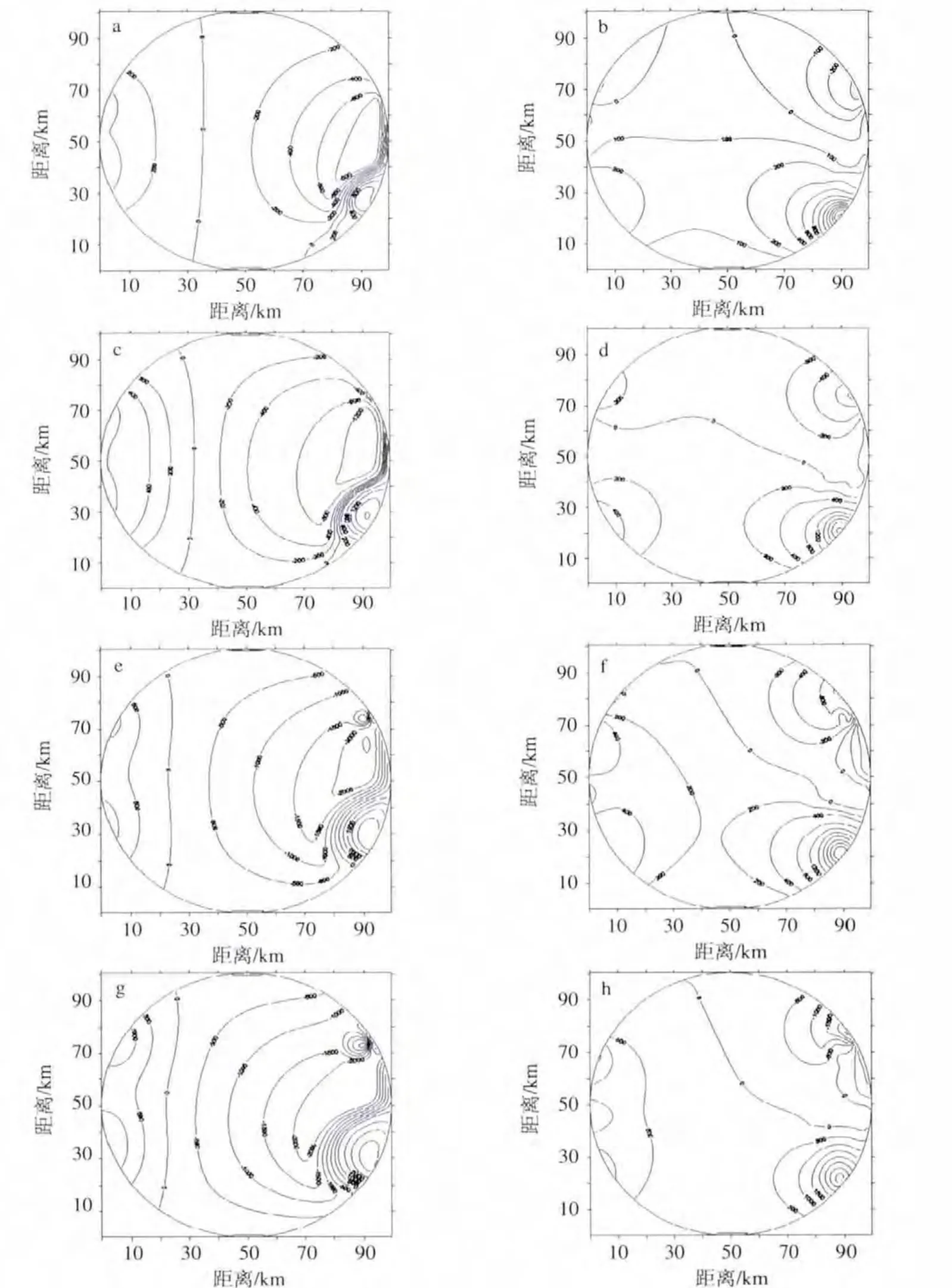
图8 表层积分48 h水体急流驱动下涡旋流场流函数(a，c，e，g)与势函数(b，d，f，h)分布形势(单位:s－1) a，b.流量 100 m3/s;c，d.流量 500 m3/s;e，f.流量 1 000 m3/s;g，h.流量 1 500 m3/sFig.8 (a，c，e，g)Stream function and(b，d，f，h)potential function of surface flow patterns driven by water jet current in 48 h(units:s－1) a，b.at jet flux 100 m3/s;c，d.at jet flux 500 m3/s;e，f.at jet flux 1000 m3/s;g，h.at jet flux 1 500 m3/s

图9给出了两类涡旋的显著差异:风应力驱动的涡旋更为深厚，从表面直至底层(图9a)。其中涡旋中心流函数等值线稀疏，说明涡旋整层流动垂直切变小。而急流驱动的涡旋与急流厚度对应，主要仅伸展至急流底部，即表层下第5层(图9b)。因此，两类涡旋的垂直形状不同，风生水体涡旋呈圆柱形，而水体急流涡旋呈碗锥形。其次，非均匀风应力场生成的涡旋强度弱于水体急流生成的涡旋强度，在图6a中，风生正涡旋中心的流函数值大约为－900 s－1，而图8g中的水体急流生成的负涡旋流函数值达3 000 s－1，两涡旋中心强度相差可达3倍以上。显然这与水体急流流速强于风应力驱动的水体流速有直接关系。

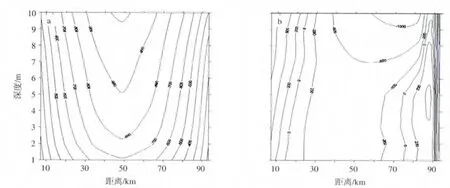
图9 积分48 h风场与急流生成的沿水体涡旋中心的垂直剖面流函数分布(单位:s－1)a.风生涡旋(A型风场)流函数剖面;b.水体急流涡旋(流量1 500 m3/s)流函数剖面Fig.9 Cross-section of stream function at eddy center driven by wind and jet current respectively in 48 h(units:s－1) a.driven by wind pattern A;b.driven by jet current(at jet flux 1 500 m3/s)

4 风场与急流共同作用下的涡旋动力特征

4.1 A型、B型非均匀风场与急流的共同作用

对A型非均匀风场分别叠加100、500、1 000、1 500 m3/s流量急流进行模拟试验，图10a、b给出了与1 500 m3/s流量急流叠加48 h的表层流函数与势函数分布特征。同时对B型非均匀风场也分别叠加 100、500、1 000、1 500 m3/s流量急流进行模拟，获得与1 500 m3/s流量急流叠加48 h的表层流函数与势函数分布特征，如图10c、d所示。

图10显示，当A型非均匀风场和急流共同作用时，风应力场产生的南北两个正负涡旋与水体急流产生的东西两个正负涡旋叠加，北部的两个正涡旋合并，中心偏向东侧，南部的两个负涡旋，保持分离状态并列存在，可以看出风场和急流两者的叠加效果。相应的势函数，在表层，南侧的两个反气旋式涡旋对应的是辐散区，北侧的气旋式涡旋对应的是辐合区。

当B型非均匀风场和急流共同作用时，由于B型风场正涡旋占主导，因此与水体急流叠加后，急流西侧的正切变正涡旋与B型风场涡旋合并，全场环流主体为正涡旋，并且流函数中心值显著增强，超过叠加前两正涡旋流函数中心值之和，达到40 000 s－1。对应的势函数清晰显示，急流入口区为辐散区和辐散中心，急流出口区为辐合区和辐合中心。全场势函数量值超过叠加前两类流场势函数中心值之和。

综上所述，强迫形成的水体涡旋整体结构形状多样，有深厚的整层一体的，也有浅薄的仅维持在上层，还有存在上下层反向等多种形式。

4.2 涡旋环流正、斜压成分演变特征

根据模式模拟的风应力场和水体急流作用下的涡旋环流速度场，将运动分为正压部分与斜压部分，即整体平均环流与偏差环流，分析涡旋环流的正压与斜压特征，以及两部分间的能量转换特征。首先分析环流的正压模与斜压模，正压模表示水平流场整层正压分量的大小，斜压模反映整层流体水平流场斜压分量(偏差环流)的大小。流场分解如下:

取A型非均匀风场与急流共同作用的流场，在流场中取2个涡旋局部强流区域，区域1为风应力驱动为主的涡旋边缘强流区，区域2为水体急流驱动为主的涡旋边缘强流区，具体如图11a所示，2个区域的正压模和斜压模随时间变化和对比见图 11b、11c。

图10 积分48 h A型风场和B型风场与水体急流叠加的流函数及势函数水平分布(单位:s－1)a.A型风场与流量1 500 m3/s急流叠加的表层流函数分布;b.A型风场与流量1 500 m3/s急流叠加的表层势函数分布;c.B型风场与流量1 500 m3/s急流叠加的表层流函数分布;d.B型风场与流量1 500 m3/s急流叠加的表层势函数分布Fig.10 Stream function，potential function fields driven by wind pattern A-B and jet current in 48 h(units:s－1) a.stream function field of wind pattern A at jet flux 1 500 m3/s;b.potential function field of wind pattern A at jet flux 1 500 m3/s;c.stream function field of wind pattern B at jet flux 1 500 m3/s;d.potential function field of wind pattern B at jet flux 1 500 m3/s

图11 A型风场与水体急流共同驱动的流场及其区域正压模与斜压模对比 a.环流流场(单位:cm/s)及两对比区位置;b.1区正压模与斜压模;c.2区正压模与斜压模Fig.11 Vortex circulation driven by wind pattern A and water jet and their regional bartropic and barclinic modes a.the flow field(units:cm/s)and the two calculating areas;b.the flow bartropic and barclinic modes in area 1;c.the flow bartropic and barclinic modes in area 2

图11b显示，区域1以正压成分为主，正压成分随时间演变稳定在0.08 m·s－1附近，斜压成分很弱，基本在0.01 m·s－1附近，随时间没有增长。因此风应力驱动的涡旋正压性为主，即整层趋于一致，同时因流速小，该区动能也相对小于区域2;图11c显示，区域2以斜压性为主，斜压成分基本在0.2 m·s－1附近，而正压成分大约达到 0.05 m·s－1，斜压成分是正压成分的4倍，因此水体急流驱动的涡旋因急流的垂直强切变而具有强的斜压性，即随深度流动变化显著，同时因流速大，该区动能也相对强于区域1。

有关区域内整层正压和斜压成分之间的动能转换，可以通过表达式计算，以KM为正压动能，KS为斜压动能，正斜压动能转换项可表示为:

对图11中的两个区域分别计算正斜压动能转换的三项，结果如图12所示。

C1表示正、斜压流场的标量相互作用及斜压流场的辐合辐散对转换项的贡献。C1＞0(＜0)，斜压动能向正压动能转换(正压动能向斜压动能转换)。图12a中C1＞0，即有斜压动能向正压动能转换，有利于维持正压型涡旋的稳定持续。图12b中，C1≈0，即该项对此区域动能转换几乎无贡献。C2表示正、斜压流场的矢量相互作用及斜压流场涡度效应对转换项的贡献。C2＞0(＜0)，斜压动能向正压动能转换(正压动能向斜压动能转换)。图12a和图12b中均有C2＞0，有斜压动能向正压动能转换，在区域1，此种转换有利于维持正压型涡旋，在区域2此种转换由矢量叉乘部分贡献，主要影响涡旋的深度。C3表示正压动能的正压平流项。C3＞0(＜0)，斜压动能向正压动能转换(正压动能向斜压动能转换)。图12a中C3＞0，斜压动能向正压动能转换，图12b中C3＜0，正压动能向斜压动能转换，这与两区域的正压型和斜压型主成分一致，均有利于这两个区域正负涡旋的维持。区域1正压成分为主，且整层平均量值小于斜压成分为主的区域2，因此区域1的转换能量显著小于区域2。

5 结论

对水体涡旋产生的主要影响因子，通过数值模拟，重点分析在确定的环境圆形边界和一定的中纬度地转偏向力作用下，非均匀风应力场与不同流量水体急流配合，形成各种涡旋的结构特征及因子作用。主要归纳为以下结论:

1)非均匀分布的风应力场，是水体涡旋产生的重要影响因子之一。不同类型的风场急流配置通过对水体表面的强迫，获得水面对风应力的响应，继而出现与风急流对应的水体急流流动。在此类急流两侧的流速切变，造成正负反向的中尺度涡旋，并且厚度深。在表层，这类风应力急流为倾斜流，具有倾斜的水面。同时正涡旋中心具有下凹表面，负涡旋中心具有上凸的表面。

2)水体急流是涡旋产生的另一重要影响因子。水体中急流的作用受到急流本身特征与强度的影响，影响范围主要在急流两侧和急流所在高度。比较风应力场产生的涡旋与水体内部急流侧向切变产生的涡旋结构，风场造成的涡旋比较深厚，而水体内部急流造成的涡旋垂直结构比较浅，但强度随水体急流的流量强度增加，流速与强度均大于风场强迫的涡旋与环流。

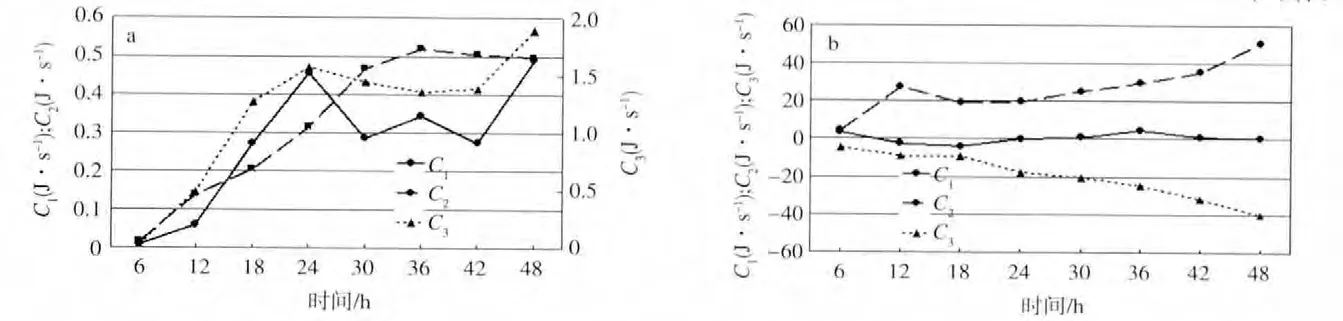
图12 两个区域的能量转换项(单位:J·s－1)随时间演变 a.区域1的三项能量转换演变;b.区域2的三项能量转换演变Fig.12 The variations of energy conversion(J·s－1)with time in the two areas a.the evolution and transformation of three types of energy in area 1;b.the evolution and transformation of three types of energy in area 2

3)地形与地转偏向力对水体涡旋形成的作用是地型边界阻挡起着引导涡旋环流走向的作用;同时因为北半球地转偏向力指向流动的右方，地转偏向力对加强急流侧向负涡旋形成和强度增强更为有利，造成负涡旋强度(绝对值)大于正涡旋强度(绝对值)。此外，正涡旋对应的辐合辐散势函数强于负涡旋，造成正涡旋区垂直上升运动强于负涡旋中垂直下沉运动。

4)在非均匀风场与急流叠加的作用下，产生的水体涡旋较为复杂，涡旋数量增加，尺度减小。底层的流场形态及强度与表层的差异大。在非均匀风场及急流叠加的作用下，强迫形成的水体涡旋垂直结构呈现多种形态:深厚的整层一致，浅薄的仅维持在上层，上下层反向流动以及上层水平流速快、中下层为波状起伏流速慢等不同形式。

5)风应力驱动的涡旋以正压性为主(整层一致性强)，水体急流驱动的涡旋因急流的垂直强切变而具有强的斜压性，根据正斜压动能的转换分析，正压动能的正压平流项对风应力驱动的水体涡旋区有斜压动能向正压动能转换，对水体急流驱动的涡旋区有正压动能向斜压动能转换，这与两区域的正压型和斜压型主成分一致，均有利于这两个区域正负涡旋的维持。

白莉娜，任福民，宋金杰，等.2010.潜热通量异常对西北太平洋热带气旋活动影响的机理研究［J］.海洋学报，32(4):32-40.

曹振东，娄安刚.2011.基于FVCOM的渤海冬季三维风生环流数值模拟［J］.中国海洋大学学报:自然科学版，41(增刊):374-378.

陈长胜.2003.海洋生态系统动力学与模型［M］.北京:高等教育出版社.

陈更新.2010.南海中尺度涡的时空特征研究［D］.青岛:中国科学院研究生院/海洋研究所.

陈红霞.2008.东海南部流—涡结构分析与动力机制研究［D］.青岛:中国科学院研究生院/海洋研究所.

陈建萍.2003.武汉暴雨过程中正斜压流场的演变特征及机理研究［D］.南京:南京气象学院.

陈淑敏，黎伟标，Lu Youyu，等.2008.南海特殊区域地形摩擦对热带气旋以及海气间潜热通量的影响［C］//中国气象学会2008年年会天气预报准确率与公共气象服务分会场论文集.烟台:中国气象学会.

程旭华，齐义泉.2008.基于卫星高度计观测的全球中尺度涡的分布和传播特征［J］.海洋科学进展，26(4):447-453.

冯兴如，杨德周，尹宝树.2010.FVCOM在龙口海域潮汐潮流模拟中的应用研究［J］.海洋科学，34(6):94-99.

管秉贤，袁耀初.2006.中国近海及其附近海域若干涡旋研究综述I.南海和台湾以东海域［J］.海洋学报，28(3):1-16.

桂海林，周兵，金荣花.2010.2007年淮河流域暴雨期间大气环流特征分析［J］.气象，36(8):8-18.

贺志刚，王东晓，陈举，等.2001.卫星跟踪浮标和卫星遥感海面高度中的南海涡旋结构［J］.热带海洋学报，20(1):27-35.

离爱兵，张立凤，臧增亮，等.2012.有限区域求解流函数和速度势的迭代调整方法及其收敛分析［J］.应用数学和力学，33(6):651-662.

李建辉，岑瑾，梅宁.1985.初夏长江中下游边界层的西南风急流及其对强对流天气的贡献［J］.气象科学，5(2):44-52.

刘泽，陈才生，侯一绮.2009.台湾北部海域黑潮与中尺度涡旋研究进展［J］.海洋科学集刊(49):1-9.

王桂华.2004.南海中尺度涡的运动规律探讨［D］.青岛:中国海洋大学.

王坚红，耿姗姗，苗春生，等.2011.近海水动力要素对入侵台风响应的FVCOM 数值模拟研究［J］.气象科学，31(6):694-703.

谢安，白人海.1995.有限区域旋转风与辐散风分解方案的选择［J］.热带气象学报，11(3):269-275.

徐晓华，廖光洪，许东峰.2010.西北太平洋反气旋涡的Argos浮标观测结果分析［J］.海洋科学研究，28(4):1-13.

尹东屏，吴海英，张冰，等.2007.2006年7月19—20日苏中地区强降水成因分析［J］.气象科学，27(6):641-647.

袁耀初，管秉贤.2007.中国近海及其附近海域若干涡旋研究综述——Ⅱ东海和琉球群岛以东海域［J］.海洋学报，29(2):1-17.

赵杰.2010.吕宋海峡东侧海区中尺度涡旋统计特征及对黑潮平均流的影响初探［D］.青岛:中国海洋大学.

赵巧华，朱广伟，邱辉.2011.太湖沉积物空间分布的风生流输送机制分析［J］.水利学报，42(2):173-179.

周玉淑，李柏.2010.2003年7月8—9日江淮流域暴雨过程中涡旋的结构特征分析［J］.大气科学，34(3):629-639.

朱宗申，朱国富，张林.2009.用有限区域风速场准确求解流函数和速度势场的方法［J］.大气科学，33(4):812-824.

Chen C S，Liu H D.2003.An unstructured grid，finite-volume，three-dimensional，primitive equations ocean model:Application to coastal ocean and estuaries［J］.J Atmos Oceanic Technol，20:159-186.

Chen C，Beardsley R C，Cowles G.2006.An unstructured grid，finitevolume coastal ocean model-FVCOM user manual［R］//Tech.Rep.SMAST/UMASSD-06-0602，Bedford，UK:318.

Colle B A.2004.Sensitivity of orographic precipitation to changing ambient conditions and terrain geometries:An idealized modeling perspective［J］.J Atmos Sci，61(5):588-606.

Robinson E A.1984.Eddies in marine sciences［J］.Int J Biometeor，28(4):326.

Wang G H，Su J L，Li R F.2005.Mesoscale eddies in the South China Sea and their impact on temperature profiles［J］.Acta Oceanologic Sinica，24(1):39-45.

Wang X C，Yi C，John F，et al.2012.Coastal ocean forecasting systems and their applications［C］//大气科学前沿发展国际研讨会暨重点实验室年会文集.南京:26-27.