雨滴下落过程谱分布演变的数值模拟

张宇，牛生杰，贾星灿

(1.南京信息工程大学大气物理学院，江苏南京210044;2.中国科学院大气物理研究所云降水物理与强风暴实验室，北京100029)

0 引言

雨滴谱是降水最基本的微物理特征量，是雨滴数浓度随雨滴尺度变化的函数。通过研究雨滴谱，可以更清楚地了解降水的发展演变过程，并且对遥感反演降水、污染物的湿清除、水土保持等方面也具有重要的现实意义。雨滴在下落过程中受到重力、空气浮力和阻力的共同作用，并且在出云到地面的过程中，雨滴本身又会受变形破碎、碰撞合并、蒸发等微物理过程共同影响，因此对于雨滴下落过程演变的研究，有一定的困难。国内外学者以实验室观测为基础，发展数值模拟，对雨滴下落的演变做了一系列有意义的研究。

国外学者从20世纪50年代开始研究雨滴的下落演变。Telford(1955)最早给出了雨滴的随机收集模式。Komabayasi(1965)给出了雨滴破碎中一个重要参数P的计算公式。Srivastava(1971)、Danielsen et al.(1972)和Young(1975)用水滴做研究，建立了水滴下落过程的合并破碎方程，用来综合考虑水滴下落过程中合并破碎机制的作用，得到了较好的实验结果。McTaggart-Cowan and List(1975)用5个雨滴做碰撞破碎研究，定义了4种直接碰撞破碎的类型，分别为丝状破碎、条状破碎、盘状破碎和包状破碎，并指出包状破碎是大雨滴的主要消耗机制。Low and List(1982)用6组水滴做实验，得到的碰并系数与McTaggart-Cowan and List(1975)的结果一致，并得出碰撞动能从高到低为盘状、条状、丝状。List et al.(2009a，2009b)用 6 组雨滴做实验，研究雨滴谱500～1 000 hPa的演变，发现在大的碰撞动能下，随着气压降低破碎数增加，高层和底层破碎和碰并对质量传输的作用很相似;并提出了新的参数，指出新参数对小雨强降水不适合，但适合于大雨强降水模式，新参数使得计算更稳定。

雨滴下落过程中碰撞破碎方程的计算方法，对雨滴下落模型影响很大，是研究的重要内容。20世纪70年代，Bleck(1970)简化了雨滴的随机收集方程。Tzivion et al.(1987)在Bleck算法的基础上，提出了高阶合并算法，比Bleck算法更有效更省时。Feingold et al.(1988)随后将 Tzivion et al.(1987)的高阶合并算法引入到破碎方程中，证明解析方法的二阶计算比一阶精确，该算法使得破碎方程总体质量守恒。McFarquhar(2004)提出了雨滴碰撞破碎新的表述方法，并指出丝状破碎是产生0.26 mm峰值的主要原因。Beheng et al.(2006)使用纳维—斯托克斯方程处理雨滴碰撞问题，这种理论计算方法对现在的数值模式仍然有研究作用。上述研究侧重研究雨滴自由下落的破碎、碰撞和合并，提出和不断发展的经验参数和理论公式对之后的降水模式有很大作用。

由于观测的局限性，20世纪80年代开始，国外学者开始基于已有的理论基础，利用模式模拟雨滴的下落过程。Gillespie and List(1978)给出破碎函数，研究雨滴碰撞过程，并根据观测数据认为M-P分布不能精确描述实际雨滴谱型，碰撞合并不能产生直径大于3 mm的大滴，直径5 mm以上的大滴可能是由于霰粒子融化产生的。Feingold et al.(1991)在模式中考虑蒸发和下沉气流，他们认为蒸发消耗大粒子使最小粒子(D≤0.1 mm)增加，但不改变峰值相位;下沉气流在忽略收集和破碎的条件下会被高估50%。郭学良等(1999)建立了层状云的雨滴分档模式，并结合部分实测资料，对中国北方常见的典型层状云降水的降水强度及地面雨滴谱进行数值模拟，结果表明，雨滴分档模式较一般使用单参数(M-P分布)的参数化模式更能反映雨滴的自然演变特征。但模式对雨滴的下落过程描述不详细，没有雨滴之间的随机碰并。在实际观测中发现，由于雨滴下落过程受多种机制影响，使得雨滴谱在空中和地面的形态有差别。以往的云模式中，详细考虑了云中各相态粒子之间的转换过程，而对于出云后雨滴落到地面的过程则描述不够详细。

牛生杰等(2002)通过分析宁夏6 053份雨滴谱资料认为宁夏地区较低的湿度造成了雨滴下落过程中蒸发较大，使得小雨强下的雨滴谱窄且数浓度较低。贾星灿和牛生杰(2008)利用宁夏实测资料，得出在雨滴到达地面的过程中，大雨滴蒸发破碎，消耗明显。Niu et al.(2010)分析宁夏雨滴谱资料后认为可能是地形因素和高蒸发率造成了宁夏地区较小的雨滴平均直径，空气密度对雨滴下落速度影响显著。封秋娟等(2007)通过分析吉林一次层状云降水的特征，给出了云滴谱和雨滴谱的拟合公式。林文和牛生杰(2009)指出层状云降水的雨滴瞬时谱谱型多呈指数分布。周毓荃等(2011)通过研究云参数特征与降水的相关性，发现层状云和对流云的降水概率均随云顶高度的增加而增大。郑娇恒和陈宝君(2007)通过比较M-P和Gamma分布对谱浓度、数浓度、雨强和雷达反射率因子的拟合效果发现，两种分布对这些特征量的拟合效果，在降水较强时差异很小，在降水较弱、小滴偏少时则差异较大。

本文利用一维雨滴分档模式，模式以银川地区一次飞机探测获得1 500 m高度的雨滴谱作为初始层，考虑了蒸发、碰并和破碎过程，模拟雨滴出云后下落过程中的谱演变。并将模拟的地面雨滴谱与实测资料进行对比，详细分析了雨滴在空中下落时蒸发、碰并和破碎等微物理过程对其影响，为雷达反演雨滴谱等工作提供更加完善的理论基础。

1 资料

对1982年7月9日发生在宁夏银川的一次雨层云降水过程进行观测，收集了空中和地面雨滴谱样本，以获得同一次降水过程中的空中和地面雨滴谱资料。降水云云底高度为1 500 m，零度层高度为4 300 m。利用色斑法对雨滴进行观测，所用吸水滤纸面积为30 cm×30 cm，其读数面积为500 cm2，取样时保证每张滤纸上雨滴约300个，暴露时间小于60 s。地面取样于银川站观测场进行，记录取样时间，每次取样间隔5 min。空中取样在飞机上进行，将取样板水平伸出机窗1.5 m，收集打落在取样板上的雨滴。取样间隔分别为0.5、1、2 min。本次观测共获得21个地面雨滴谱样本，59个空中雨滴谱样本。

2 模式介绍和计算设计

2.1 模式介绍

模式中考虑的雨滴下落过程为出云后的过程，因此水成物只有雨滴。假定雨滴在垂直方向自由下落，因此是一维模式。使用郭学良等(1999)的雨滴下落末速度计算方法:

其中:Di为第i档雨滴直径;ρ为空气密度，本文使用宁夏当地空气密度。

模式变量包括雨水质量混和比q和雨滴分档数浓度N。

模式的控制方程为:

(1)式用于计算降水场q;(2)式用于计算雨滴分档数浓度 N。其中:Vi为第 i档的雨滴下落速度;EVAP和SC/SB(stochastic collection and stochastic breakup)分别表示由于蒸发和随机增长引起的微物理量的改变。

模式中一共考虑了3种微物理过程，分别是蒸发过程、破碎过程和碰并过程。

2.1.1 蒸发过程

模式计算雨滴下落过程中的蒸发率，利用郭学良等(1999)应用的单个雨滴蒸发率的计算方程:

其中:Df为水汽扩散系数;k为空气热传导率;f(Re)为雨滴的通风因子，Re为雨滴的雷诺数;Di为第i档雨滴的直径;qv和qvs分别为水汽比湿和饱和水汽比湿;Lv为水汽潜热;Rw为湿空气比气体常数;T为环境温度;es为饱和水汽压。

2.1.2 随机碰并和随机破碎过程

雨滴在下落过程中由于下落末速度的差异，会发生碰并和破碎现象。雨滴的随机增长模型很好地描述了这个现象，经过多年发展，已有较成熟的处理方法。随机增长模型包括随机碰并和随机破碎两个部分，只有随机碰并时，雨滴越来越大，加入随机破碎后才能得到符合理论的准定常的雨滴谱分布，例如 M-P 分布(Pruppacher and Klett，1996)。

Feingold et al.(1988)使用高阶算法处理雨滴随机增长方程，得到更加精确的结果。本文处理雨滴随机碰并和破碎时，采用该方法。Yin et al.(2000)的二维分档云模式也使用此方法处理雨滴的随机增长过程。雨滴随机增长方程如下:

其中:等号右边前两项表述的是碰并过程，后两项表述的是破碎过程。n(m，t)是在t时刻用质量m表示的雨滴尺度谱。C(x，y)和B(x，y)分别为收集系数和破碎系数:

其中:K(x，y)是质量为x和质量为y的水滴的重力碰并系数;E(x，y)是x和y雨滴对应的碰并效率;P(x;m，y)是质量为m和y的两个雨滴碰撞后产生质量为x的雨滴的分布函数。在此假设碰并过程和破碎过程是相互独立的，不考虑反弹作用。

2.1.3 分档方案和计算过程

本文分档模式选用的分档方案为质量分档方案，它的设计不同于体积水参数化方案，用以计算各档雨滴的质量和数浓度。参考Yin et al.(2000)的分档方法，模式中液态水粒子分为34档，第二档粒子质量为第一档的两倍，

粒子质量的第一档和最后一档分别为1.597 9×10－14kg和1.372 6×10－4kg，对应的直径分别为3.125 0×10－3mm和6.400 0 mm。

模式计算的破碎过程为碰撞破碎过程，认为任意两档的雨滴之间都可以发生碰撞破碎。

模式中，在一个积分步长中，某个高度第i档粒子总质量M变到M*由下式给出:

M*=M+m1+m2+m3。

其中:m1为高层输入;m2为蒸发改变量;m3为碰撞破碎引起的该档粒子的总改变量。

模式假设粒子以下落末速度下降，首先计算每档粒子的下落末速度，然后计算在一次积分步长中粒子的下落距离，计算一次积分步长内粒子蒸发引起的质量改变，同时计算这个高度中各挡粒子之间碰撞引起的质量改变，进而得到改变后各档粒子的质量浓度。

2.2 模式初始化设计

模式中各层温度和湿度由实测资料拟合输入，地面气压为1 000 hPa，模式第一层的高度为1 500 m，模式在垂直方向上分为1 001层，每层间隔1.5 m，设置积分时间步长为5 s。

模式需要输入垂直每层温度(T)和露点温度(Td)，根据飞机实测资料，对温度随高度的变化进行线性拟合，再放入模式中，同样根据实测温湿资料，计算露点温度，做露点随高度的拟合曲线，放入模式中。对温度随高度变化的拟合结果为T=24.365 4－0.005 9H，R2=0.954 5;对露点温度随高度变化的拟合结果为Td=16.908 1－0.006 61H，R2=0.552 2。

第一层雨滴谱由实际观测资料做M-P分布拟合给出，计算该层不同档雨滴在下落过程中的下落末速度、蒸发、碰并和破碎，再进入下一层。

对雨滴谱拟合通常有两种方法:M-P和Gamma分布。M-P分布的形式为N=N0exp(－λD)。其中:D为雨滴直径;λ为斜率因子;N0为总数浓度。Gamma分布的形式为N=N0Dμexp(－λD)。其中:μ为形状因子。本文采用M-P分布拟合实测雨滴谱。图1给出了1 500 m高度的平均雨滴谱分布和M-P分布的拟合谱，这个拟合谱作为模式的第一层初始谱，拟合公式为N=106.589 7exp(－1.023 6D)，

图1 1 500 m高度的实测平均雨滴谱和M-P分布拟合曲线Fig.1 Measured mean raindrop size distribution at 1 500 m and its fitting curve in M-P distributionR2=0.831 5。

3 结果分析

3.1 模式验证

将以上所得M-P分布作为初始时刻的分布输入模式中，设定积分60 min，取1 200 m高度层附近的模拟结果对比本次观测结果，给出1 200 m处模拟和实测的雨滴谱(图2)。选用的模拟结果直径为0.2～2.4 mm，因为观测结果在这个直径范围内。由图2可以看出，模拟谱和实测谱的趋势基本一致，能够模拟出雨滴谱的多峰现象，并且模拟出了大滴一侧的峰值。直径小于1 mm的部分，模拟值和观测值较为接近，大于1 mm的部分，观测值要比模拟值大。

图2 1 200 m高度雨滴谱的观测结果和模拟结果Fig.2 The measured and simulated raindrop size distribution at 1 200 m

本次观测共取得21个地面雨滴谱样本，计算21个样本的雨强、总数浓度和雷达反射率因子等参量，发现有3个样本的参量明显与其他样本有差别，这3个样本使各个参量的平均值增大，故计算地面平均雨滴谱时，不使用这3个样本。去除这3个样本后，得到本次观测的地面平均雨滴谱(图3)，观测结果在2.8～3.0 mm的数密度为0。选用积分60 min时靠近地面几层的模拟结果，直径为0.2～3.2 mm。由地面的平均雨滴谱(图3)可见，实测谱的斜率大于模拟谱，与1 200 m情况相反，在直径小于1 mm的部分，模拟结果小于实测结果，大于1 mm的，模拟结果大于观测结果。观测结果在2 mm处数密度发生增加现象，而模拟结果是在1 mm处。

3.2 雨滴下落的影响机制

雨滴在下落过程中哪种影响因子更重要呢?为了解决这个问题，设计了一组对比试验:1)综合考虑蒸发、碰并和破碎过程的雨滴模拟;2)只考虑碰并和破碎作用的雨滴模拟;3)仅考虑蒸发作用的雨滴模拟。

为了得到更加精确的结果，模式设定的积分总时间为60 min，模式结果每5 min输出一次，得到各高度层不同直径雨滴数密度的演变(图4)。对比图4a、b可以发现，5 min时，直径大于1 mm的雨滴已经降落到地面，10 min时，地面附近小雨滴(D＜0.3 mm)部分数密度仍然小于0.546 9 m－3·mm－1，表明模式中小雨滴部分靠重力作用降落到地面所需的时间超过10 min。总积分时间达到20和60 min时(图4c、d)，小雨滴已经降落到地面，形成较稳定的雨滴谱。由20到60 min的雨滴谱演变发现，数密度峰值在小雨滴区域变化，直径大于1 mm的雨滴谱在积分20 min后就比较稳定，变化较小。

图3 地面平均雨滴谱的观测结果和模拟结果Fig.3 The measured and simulated raindrop size distribution on the ground

图4 积分5 min(a)、10 min(b)、20 min(c)、60 min(d)的各高度层不同直径雨滴数密度的演变(单位:m－3·mm－1;综合考虑蒸发、碰并和破碎作用模拟;数密度值小于0.546 9 m－3·mm－1的区域显示为空白)Fig.4 Evolution of number density of raindrops of different diameters at different altitudes(units:m －3·mm －1;comprehensively considering evaporation，coalescence and breakup;the blank area indicates the number density less than 0.546 9 m －3·mm －1) a.5 min;b.10 min;c.20 min;d.60 min

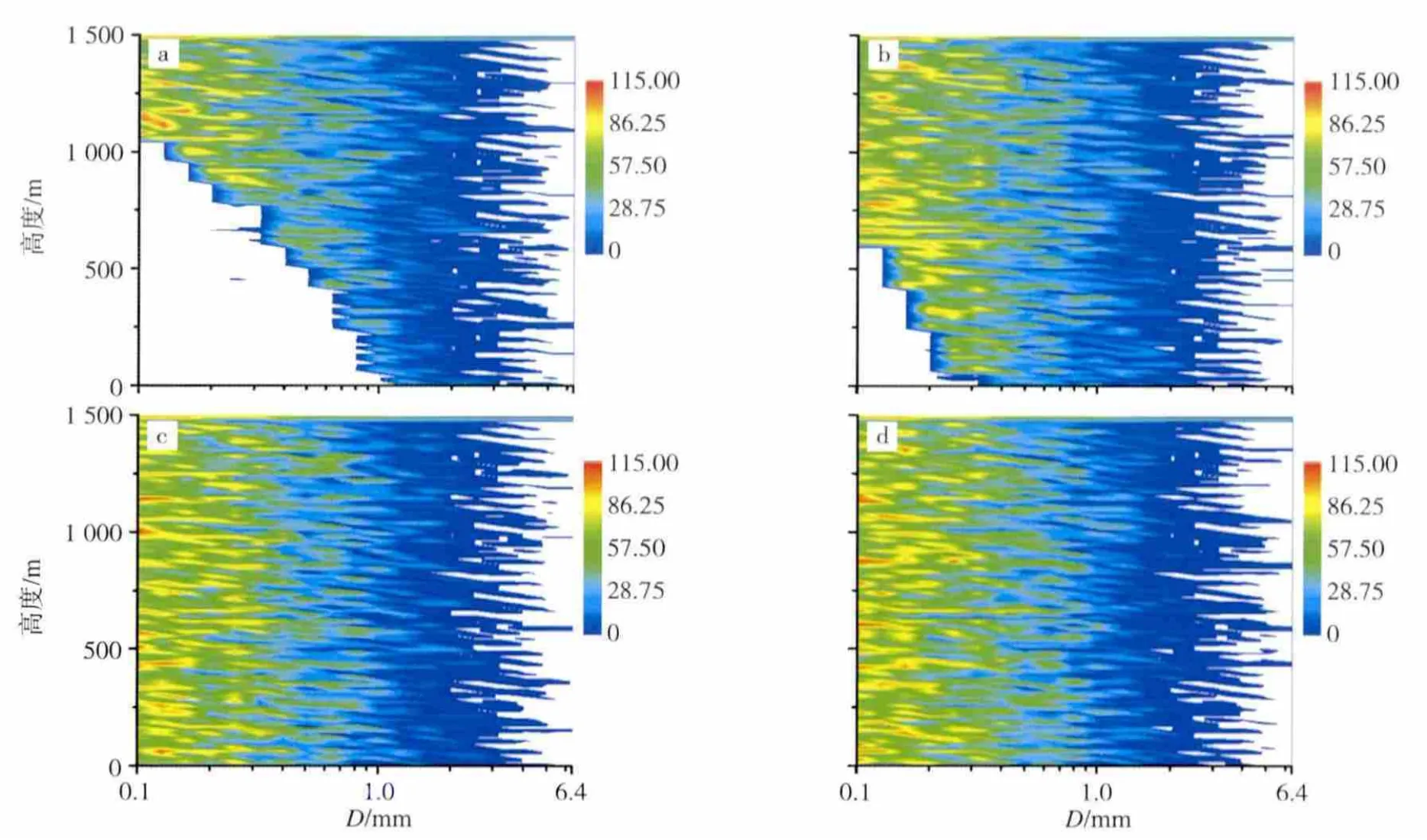
图5 积分5 min(a)、10 min(b)、20 min(c)、60 min(d)各高度层不同直径雨滴数密度的演变(单位:m－3·mm－1;只考虑碰并和破碎作用模拟;数密度值小于0.449 2 m－3·mm－1的区域显示为空白)Fig.5 Evolution of number density of raindrops of different diameters at different altitudes(units:m －3·mm －1;only considering coalescence and breakup;the blank area indicates the number density less than 0.449 2 m －3·mm －1) a.5 min;b.10 min;c.20 min;d.60 min

图6 积分5 min(a)、10 min(b)、20 min(c)、60 min(d)的各高度层不同直径雨滴数密度的演变(单位:m－3·mm－1;只考虑蒸发作用模拟;数密度值小于0.462 9 m－3·mm－1的区域显示为空白)Fig.6 Evolution of number density of raindrops of different diameters at different altitudes(units:m －3·mm －1;considering evaporation only;the blank area indicates the number density less than 0.462 9 m －3·mm －1) a.5 min;b.10 min;c.20 min;d.60 min

图5和图6分别是只考虑碰并和破碎和只考虑蒸发的各高层雨滴谱演变，可以看出，蒸发作用基本不改变雨滴谱的谱型，碰并和破碎则会产生一些新的数浓度峰值，使得雨滴谱为双峰型或者多峰型。

对比图5a、b，可以发现，小雨滴(D＜0.3 mm)没有到达地面，说明10 min时，仅靠碰并和破碎作用无法在地面产生大量的小雨滴。对比图4a、图5a和图6a中1 100 m以下的各层谱宽，综合考虑3种作用(图4a)和只考虑蒸发作用(图6a)比只考虑碰并破碎作用(图5b)的谱宽略宽。分析图4b、图5b和图6b中600 m以下的谱宽，得到了相同的结果。

对比图4b、图5b和图6b，可以看出，10 min时，只考虑碰并和破碎作用的模拟结果(图5b)，50 m以下直径为0.3 mm的区域存在一些小粒子，数浓度较小，而综合考虑3种作用(图4b)和蒸发作用(图6b)却没有产生这些小粒子，表明图4b中，这个区域内碰撞破碎作用产生的雨滴被蒸发作用所消耗掉。说明蒸发作用对于小雨滴有很明显的消耗作用。对比图4、图5和图6，发现中等大小的雨滴(0.3 mm≤D≤1 mm)的数密度，只有蒸发作用和3种综合作用的都大于只有碰并破碎作用的，说明蒸发作用使得中等大小的雨滴数密度增加。

模拟结果中，综合考虑3种作用和只考虑碰撞破碎作用产生的数密度峰值的位置大致相同，但是综合考虑3种作用的数密度峰值为140 m－3·mm－1，只考虑碰并和破碎作用的数密度峰值为115 m－3·mm－1，只考虑蒸发作用的数密度峰值为118 m－3·mm－1，这说明数密度峰值是由蒸发和碰撞破碎共同作用产生的。

综上所述，模式较好地反映出由于蒸发、碰并和破碎过程对于不同档雨滴下落过程的演变特征。

3.3 雨滴谱特征量演变

为了进一步直观地分析雨滴谱下落时的变化，计算雨滴谱的特征量:平均直径、总数浓度、滴谱散度(List et al.，2009a)以及表征单位体积内雨滴特征的雨强、雷达反射率因子。这些具有物理意义和统计意义的特征参量是雨滴谱研究的重要内容。

图7是模拟1 200 m高度处，雨滴谱的平均直径、滴谱散度、总数浓度和雨强随时间的变化曲线，可以发现，20 min内，碰并和破碎作用引起雨滴谱的平均直径减小，谱宽变大，总数浓度增加，主要是由于模拟中大粒子下落然后破碎引起的。20 min之后，平均直径、滴谱散度和总数浓度基本保持不变，说明1 200 m高空在模拟20 min后形成较稳定雨滴。同样可以看出，蒸发作用使雨滴谱的平均直径变小，谱宽变窄，数浓度减小，造成雨强也减小;而碰并和破碎作用使得雨滴谱的平均直径变大，谱宽变宽，数浓度减大，造成雨强也变大。

图8是模拟中地面上雨滴谱的平均直径、滴谱散度、总数浓度和雨强随时间的变化曲线，可以看出，模拟中地面上的雨滴谱的平均直径先增大后减小，这是由于模拟中大雨滴会先下落到地面，然后是较小的雨滴下落到地面，平均直径先增大，当小雨滴逐渐增多后，平均直径又减小了。模拟中地面达到稳定降水的时间为30 min。碰并破碎和蒸发对雨滴谱特征参量的作用与空中相同。

图7 模拟1 200 m处雨滴谱特征参量 a.平均直径;b.雨滴谱散度;c.总数浓度;d.雨强Fig.7 Simulated spectral parameters at 1 200 m a.average diameter;b.spectral divergence;c.total number concentration;d.rainfall intensity

图8 模拟地面雨滴谱特征参量 a.平均直径;b.雨滴谱散度;c.总数浓度;d.雨强Fig.8 Simulated spectral parameters on the ground a.average diameter;b.spectral divergence;c.total number concentration;d.rainfall intensity

观测结果中，单个样本中最大的平均直径、总数浓度和雨强分别为 0.83 mm、2 015 m－3、27.45 mm/h，而模拟中没有出现这种情况，说明模式对于雨强较大的降雨模拟能力不足，这方面有待下一步工作研究。

模拟结果中，各层雨滴平均直径、总数浓度、雨强和雷达反射率因子都比较小，总的原因是雨滴数浓度较小，可能是随机增长中碰撞破碎作用不够强烈而蒸发作用比较强烈造成的雨滴总数度较小，模式中的一部分有待改进。

4 结论与讨论

1)以飞机观测的空中雨滴谱和边界层气象要素廓线作为初始背景场，利用一维雨滴分档模式对雨滴出云后下落过程中的演变进行了模拟研究，并将模拟结果与地面和空中的实测雨滴谱进行对比。结果表明该分档模型对雨滴下落过程中的蒸发、碰并和破碎机制有较好的模拟能力，模拟的滴谱呈多峰分布。

2)基于模式的敏感性试验结果，详细分析了蒸发、碰并和破碎机制对雨滴谱谱型演变的影响。蒸发作用对小雨滴的消耗作用较大雨滴明显，中等大小雨滴的数目有所增多，但整体上不改变雨滴谱的谱型和分布;而碰并和破碎机制可以增大滴谱的谱型变化，并在大滴端出现第二个峰值。

总体而言，本模式对考虑了蒸发、碰并和破碎机制的雨滴出云下落过程进行了模拟，能够较好地再现出雨滴下落过程中谱型的变化。然而，目前的工作尚未考虑垂直气流和湍流的影响，在下一步的工作中有待对此方面加强。

封秋娟，牛生杰，雷恒池，等.2007.吉林省一次层状云降水宏微观特征的观测研究［J］.南京气象学院学报，30(6):770-778.

郭学良，黄美元，徐华英，等.1999.层状云降水微物理过程的雨滴分档数值模拟［J］.大气科学，23(6):745-752.

贾星灿，牛生杰.2008.空中、地面雨滴谱特征的观测分析［J］.南京气象学院学报，31(6):865-870.

林文，牛生杰.2009.宁夏盛夏层状云降水雨滴谱特征分析［J］.气象科学，29(1):97-101.

牛生杰，安夏兰，桑建人.2002.不同天气系统宁夏夏季降雨谱分布参量特征的观测研究［J］.高原气象，21(1):37-44.

郑娇恒，陈宝君.2007.雨滴谱分布函数的选择:M-P和Gamma分布的对比研究［J］.气象科学，27(1):17-25.

周毓荃，蔡淼，欧建军，等.2011.云特征参数与降水相关性的研究［J］.大气科学学报，34(6):641-652.

Beheng K D，Jellinghaus K，Sander W，et al.2006.Investigation of collision-induced breakup of raindrops by numerical simulations:First results ［ J］. Geophys Res Lett， 33， L10811. doi:10.1029/2005GL025519.

Bleck R.1970.A fast approximative method for integrating the stochastic coalescence equation［J］.Geophys Res Lett，75:5165-5171.

Danielsen E F，Black R，Morris D A.1972.Hail growth by stochastic collection in a cumulus model［J］.J Atmos Sci，29:135-155.

Feingold G，Tzivion S，Levin Z.1988.The evolution of raindrop spectra.PartⅠ:Solution to the stochastic collection/breakup equation using the method of moments［J］.J Atmos Sci，45:3387-3399.

Feingold G，Levin Z，Tzivion S.1991.The evolution of raindrop spectra.PartⅡ:Downdraft generation in an axisymmetrical rainshaft model［J］.J Atmos Sci，48:315-333.

Gillespie J R，List R.1978.Effects of collision induced breakup on dropsize distributions in steady-state rain-shates［J］.Pure Appl Geophys，117:599-626.

Komabayasi M.1965.Probability of disintegration of water drop as a factor determining size distribution of raindrops［C］//Proceedings of the international conference on cloud physics.Tokyo and Sapporo:260-264.

List R，Fung C，Nissen R.2009a.Effects of pressure on collision，coalescence and breakup of raindrops.Part Ⅰ:Experiments at 50 kPa［J］.J Atmos Sci，66:2190-2203.

List R，Nissen R，Fung C.2009b.Effects of pressure on collision，coalescence and breakup of raindrops.Part II:Parameterization and spectra evolution at 50 and 100 kPa［J］.J Atmos Sci，66:2204-2215.

Low T B，List R.1982.Collision，coalescence and breakup of raindrops，PartⅠ:Experimentally established coalescence efficiencies and fragment size distributions in breakup［J］.J Atmos Sci，39:1591-1606.

McFarquhar G M.2004.A new representation of collision-induced breakup of raindrop and its implications for the shapes of raindrop size distributions［J］.J Atmos Sci，61:777-794.

McTaggart-Cowan J D，List R.1975.Collision and breakup of water drops at terminal velocity［J］.J Atmos Sci，32:1401-1411.

Niu S，Jia X，Sang J，et al.2010.Distributions of raindrop sizes and fall velocities in a semiarid plateau climate:Convective versus stratiform rains［J］.J Appl Meteor Climatol，49:632-645.

Pruppacher H R，Klett J D.1996.Microphysics of cloud and precipitation［M］.Boston:Kluwer Academic Publishers:645-646.

Srivastava R C.1971.Size distribution of raindrop generated by their break up and coalescence［J］.J Atmos Sci，26:1272-1282.

Telford J.1955.A new aspect of coalescence theory［J］.J Atmos Sci，12:436-444.

Tzivion S，Feingold G，Levin Z.1987.An efficient numerical solution to the stochastic collection［J］.J Atmos Sci，44:3139-3149.

Yin Y，Levin Z，Reisin T G，et al.2000.The effects of giant cloud condensation nuclei on the development of precipitation in convective clouds——A numerical study［J］.Atmos Res，53:91-116.

Young K C.1975.The evolution of drop spectra due to condensation，coalescence and breakup［J］.J Atmos Sci，32:965-973.