并行燃烧数值模拟计算优化——面向自适应非结构网格的动态负载平衡方法

王 姝，王小鸽，杨广文

清华大学 计算机系，北京100084

1 引言

随着燃烧数值模拟计算技术的发展，模拟的问题越来越复杂，模拟的精度要求越来越高，传统模拟方法采用结构网格，计算较为简单，但是受到其结构特性的限制，不能灵活地根据模拟情况改变网格的结构以适应新的计算需求，因此逐渐被非结构网格所替代。相对于结构网格而言，非结构网格可以对复杂的几何外形结构进行更为准确的描述；非结构网格中的一个点周围的点数和单元数不是固定的，这一特点使得非结构网格易于调整网格结构，以适应计算的需要。

在进行燃烧数值模拟计算的过程中，部分区域的计算精度要求比其他区域高，如化学反应剧烈的区域、流场梯度变化剧烈的区域。为了提高计算精度，需要对此类区域的网格进行自适应加密，通过减小计算网格的尺度以达到需要的精度。另外，在某些不需要高计算精度的区域，为了减少计算量，对网格进行自适应减疏。

由于数值计算规模越来越大，传统的串行程序已经不能满足高效的计算需求，将数值模拟计算并行化成为迫切需求。同时，在计算并行化以后，由于计算集中在化学反应剧烈的区域，进程之间的计算负载会严重不平衡，将导致并行效率大大降低。非结构网格和网格自适应结合使用可以达到模拟计算的精度要求，但是含自适应功能以后，网格数目的变动会使负载随之变化。在这种情况下，需要在进程之间进行负载平衡调度，使计算负载均匀分布在所有进程上，使得非结构网格自适应计算模拟在提高精度的同时，缩短程序运行的时间，提高数值模拟计算的效率。

在自适应非结构网格上实现程序并行及负载平衡，最大的挑战是如何在原有数据结构的基础上正确、高效地执行程序。本文是基于文献[1]中的燃烧数值模拟和文献[2]中的非结构网格自适应方式，在充分研究了非结构网格的数据结构和非结构网格自适应变化特点的基础上，提出了一套有效的负载平衡策略，使得进程之间的负载较为平均，减少了程序总体运行时间；为了使负载转移不受非结构网格存储方式的限制，本文对非结构网格的存储方式进行了改进，使得负载转移更加容易实现。

2 相关工作

在非结构网格上实现并行和负载平衡计算逐渐成为数值模拟计算的一个重要研究方向，近几十年有许多这方面的系统和算法。国际上的许多静态负载平衡方法[3-6]是在编译阶段预测负载，并将数据和计算映射到进程上，这对于常规并行问题是很有效的，但是当问题变得非常规时（例如需要引用非本地数据或者计算迭代的开销在运行时无法预测）性能会变得很差。SUPPLE[7]结合了静态和动态负载平衡的方法，首先通过静态的方式在编译阶段预测负载和通信，程序运行时采用块为单位进行负载转移。还有很多对负载的划分基于图划分的方法[8-11]，它们的网格划分方法受到非结构网格和自适应机制的约束，很难应用到现有的数值模拟计算中。

在国内的研究中，DSMC[12]并行算法的负载平衡的指标是每个进程上的网格上的分子数量大致相当，采用交替二分法划分网格，这种划分方法的负载平衡效率较好，但会产生许多不规则的通信，容易造成程序效率低下。文献[13]采用预处理方法采用METIS 进行负载平衡和任务划分，并提出一种网格单元重排序算法提高访存命中率难点以及研究的目标。这种动态负载平衡效果较好，但是需要改变原有数据结构的存储方式。还有文献[14]采用子区域数远远小于处理器数目的方式实现动态负载，这样的处理方式可以得到较为均衡的负载，但是由于问题划分得过小，需要经常通信，会降低程序执行的效率。文献[15]在全局范围内实现网格的重新划分，这种处理方式会带来大量、经常的通信。

国外的负载平衡系统和算法绝大部分是不开源的，无法应用到现有的数值模拟计算中。而国内的处理方法大都需要灵活网格的存储方式，例如文献[13]的网格重排序和划分、文献[15]的网格重新划分等。要在尽量不改变非结构网格自适应存储方式的前提下达到负载平衡的目的，需要一种对数据存储方式要求不高的负载平衡方法。

在自适应非结构网格上实现动态负载平衡需要考虑其数据结构和自适应方式。每个网格单元上的数值需要由其相邻网格单元上的数值计算得出，如图1 的伪代码所示。

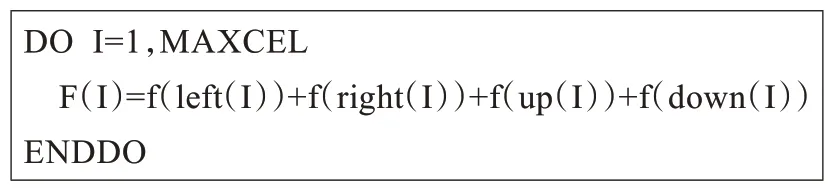
图1 单元格计算的伪代码

非结构网格中，相邻网格的存储地址是通过两个网格共享边的单元格属性数组获得的。如图2 所示。

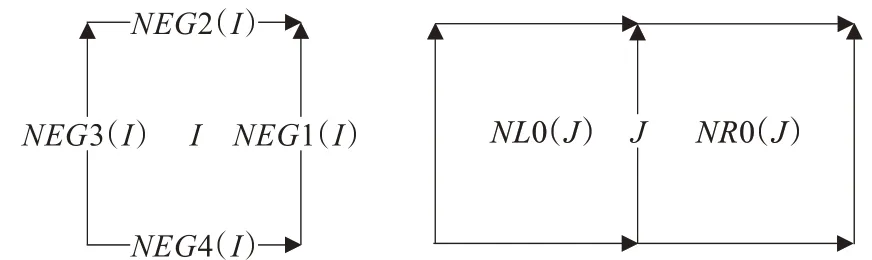
图2 边的编号、方向和单元格的关系

从图2 中可以看出，编号为I的单元格的四条边从右边开始逆时针编号，依次为NEG1(I) ，NEG2(I)，NEG3(I)，NEG4(I)。边被赋予了方向，其中水平边以向右为正方向，竖直边以向上为正方向。沿着边的正方向，左边的单元格为该边的左单元格，右边的单元格为该边的右单元格。编号为J的边的左右单元格分别为NL0(J)和NR0(J)。要想获得单元格I的邻居，以右邻居为例，则应先取它的右边NEG1(I)，然后取这条右边的右属性单元NR0(NEG1(I))，从而得到它的右邻居。

网格的自适应加密方式如图3 所示，1 号网格加密变成4 个子单元格，子单元格还可以再加密变成更小的4 个子单元格，以3 号网格为例。

图3 网格自适应加密方式

偏微分方程求解和网格自适应需要用到邻居单元格的数据，而邻居单元格通过图2 所示的关系得到。并行求解时，两个相邻网格被分配到不同的进程上，它们共享的边（即重叠边）需要分别在这两个进程上存放。在自适应加密或减疏以后，由于两个重叠边的分裂情况不同，需要更新分裂后子边对应的新重叠边。如图4（a）所示，初始时有两条均未分裂的重叠边I，J，边J先分裂成两个子边，而I未分裂（如图4（b）所示），这时边I的重叠边仍为J，边J的子边SUB1(J)和SUB2(J)的重叠边为边I。当边I也发生分裂时，边J子边的重叠边才发生更新。如图4（c）所示，I的子边SUB1(I)的重叠边为SUB1(J)，SUB2(I)的重叠边为SUB2(J)。

本文使用的实验是一个化学反应流计算程序。程序执行1 280 步，采用8 个进程（便于在图上显示）。初始网格为16×4，化学反应稳定后的网格规模在20 000 左右。化学反应使用常微分方程求解，流动使用偏微分方程求解。通过实验得出，各进程解常微分方程的时间差异很大，而解偏微分方程的时间差异不大，因此计算不平衡部分集中在解常微分方程部分。本文关注的重点在于求解常微分方程计算时间的差异，而非通常意义下的负载，即在求解过程中做了多少、什么种类的运算。为说明简便，本文后续内容中的负载均指求解常微分方程的计算负载。考虑进程间的负载变动情况，统计程序执行计算的时间（s），为使结果更清晰，将时间t取对数ln t，各进程的执行时间情况如图5所示。

图4 原网格相邻网格被分配到不同的进程示意图

图5 不同时间步上各进程的负载分布

从图5 可以看出，在程序执行初期，从1 号进程开始，负载逐渐变大，并且随着时间的推进各进程的负载陆续增加，这是第一阶段；直到第400 步左右，7，8 号进程的负载剧烈增加，这是第二阶段；到第600 步以后，各进程的负载趋于稳定，这是第三阶段。出现这种情况的原因是：第一阶段化学反应不明显，流场梯度变化剧烈的区域网格发生加密，随着该区域的位置不断转移，各进程的负载随之变化。在第二阶段，在7，8 进程的计算区域突然发生了剧烈的化学反应，导致这些区域的负载急剧增加。在第三阶段，化学反应趋于稳定，负载变动缓慢。

在文献[1]的工作基础上，为了提高计算效率，将原有并行程序进行优化。本文在原有数据结构上，根据非结构网格和网格自适应方式的特点，对非结构网格的存储方式进行了优化，提出了一套高效的负载转移方法。

3 需要考虑的问题

要在自适应非结构网格上实现动态负载平衡，需要考虑以下六个方面：

（1）非结构网格

在传统的结构网格上，网格单元使用多维数组存放，并且可以根据该数组的下标关系来访问邻接单元格，每个单元格的邻接单元格是确定的，这便于网格的剖分；而非结构网格通过一维数组存放单元格，邻居单元格的数据调用方式如图2 所示。

（2）自适应

当一个网格单元与其相邻网格的梯度超过阈值时，网格在型心点处分裂成四个，称为加密。原来的网格称为父网格，四个新产生的网格称为子网格。当一个父网格单元与其相邻网格的梯度低于某一阈值时，其四个子网格合并为一个，称为减疏。网格的自适应会导致某些网格上的计算急剧增加，加剧了进程之间的负载不平衡性，更加大了负载平衡的难度。非结构网格的这种特点使得动态负载过程中的负载划分变得困难。

（3）负载的变动

数值模拟计算一般包括两个方面：求解常微分方程和求解偏微分方程，本文使用的程序中，化学反应使用常微分方程求解，流动使用偏微分方程求解。通过分析程序可以得出：不同进程之间的化学反应计算负载差异巨大；流动计算仅与网格数目有关，而化学反应稳定以后，各个进程中的网格数量基本一致。常微分方程通过牛顿迭代求解，在剧烈化学反应开始之前，常微分方程求解计算负载仅与网格数有关；在剧烈化学反应开始之后，牛顿迭代次数急剧上升，同一单元格上的计算负载相差几百倍，因此可以得出结论：同一个网格的计算负载与当前牛顿迭代次数相关。

由于负载的变动，需要解决的问题包括负载预测的方法和负载转移的时机。即负载的变动与哪些因素有关，如何将这些因素与负载联系起来，以及在执行哪些计算时，需要负载转移。

（4）负载转移的粒度

根据数值计算系统的计算特点，求解偏微分方程需要由其邻居单元格上的数值计算得出，采用原始粗网格中的一列作为负载转移的单位，可以降低负载转移后寻找邻居单元格的难度。

（5）非结构网格自适应存储方式带来的困难

图6 原始网格

通过结合图6 和图7 来分析非结构网格自适应时存储数组的特点。假设原始网格中有1～9 号非父（没有子单元格）的单元格，按列先序一起存储在图7（a）所示的数组中。非父单元格占据数组的前半部分位置，父单元格占据数组的后半部分位置，中间未填满的部分留空。原始未加密网格的存储方式，如图7（a）所示，此时通过计算，2 号单元格需要加密。那么2 号单元格的子单元格编号为10，11，12，13，放入非父单元格末尾，如图7（b）所示。此时2 号单元格已经加密成为父单元格，需要将它挪入父单元格存储区域，即从数组末尾开始往前存放。然后将末尾的13 号单元格填补上2号单元格在非父单元格存储区域中留下的空白，如图7（c）所示。

图7 网格自适应存储方式

由于负载转移的单位为以原始粗网格中的一列，而非结构网格的存储方式是不以列为单位的，这样一来，要从如图7 所示的非结构网格存放的一维数组中挑选出第一列（1，3，10，11，12，13 号单元格）上的数据执行转移，不便于处理。这里需要解决的问题是如何改进网格自适应存储方式，达到第4 章中提出的以列为单位执行负载转移。

（6）负载转移策略

负载转移策略的目标是使通信量尽可能少，每个进程上的负载趋于一致。因此在每次负载转移之前，需要一个进程统计所有进程的负载情况，各进程负载的最大值与平均负载的比值为Max/Avg 。在负载平衡的情况下，Max/Avg为1。不平衡率越大，负载越不平衡。在进行负载调度时，判断全局的Max/Avg 是否大于某个给定的阈值，如果大于，则执行负载转移。这个阈值的大小是根据负载转移的开销和不平衡情况综合考虑的。迁移的开销越大，阈值的设置也需要大些，以避免负载平衡工作的“得不偿失”。

4 解决方案

本文的实验使用的计算节点采用两个Intel Xeon X5670六核处理器（2.93 GHz，12 MB Cache），160 GB SATA 硬盘。节点内存48 GB，结果取多次实验的平均值。

结合上一章中提出非结构网格的特点和网格自适应方式，针对需要解决的问题，本文提出的负载平衡方案具体如下。

4.1 负载预测方法

经过分析串行程序各部分运行时间，解常微分方程时间占解常微分方程和解偏微分方程总时间的34.4%。偏微分方程计算时间只与网格数目有关，常微分方程计算约90%的时间花费在牛顿迭代上，且临近时间步的牛顿迭代次数相近，因此将本时间步牛顿迭代次数作为下一时间步负载的估计。

为了更加精确地预测负载，需要选取能够进一步表征常微分方程计算负载的变量进行预测。在本实验情况下，选取化学反应放热量Q。在放热量达到某个阈值时，开始剧烈化学反应，将此阈值作为切换负载预测策略的分割点。采用这种自动切换负载预测方法的原因是：开始剧烈化学反应之前，放热量Q 不稳定，无法作为负载预测的判据，此时解常微分方程的负载与牛顿迭代次数成正比；在剧烈化学反应开始之后，放热量Q 与负载的相关性更高。通过结合两种预测方式，可以使负载的预测更接近真实情况。这种负载预测方法的效果在第5 章中分析。

4.2 负载转移时机

考虑到第3 章中提出的负载变动方式，由于解偏微分方程的计算负载只与网格数有关，化学反应稳定后各进程上的网格数目差异不大，求解偏微分方程计算负载基本平衡，因此只需在解常微分方程时执行动态负载平衡策略。

由主控进程统计所有计算进程的负载，若Max/Avg 大于某个阈值，则需要进行负载转移。

另外，为了避免自适应时重叠边的更新成为难点，采取在自适应之后执行负载转移这种方式。这样仅需把计算负载转移出去，计算完成之后更新单元格的状态即可。

4.3 数据存储方式的调整

由第3 章的描述可以得知，非结构网格的存储结构特点是：单元格在存储时没有规律可循，要从所有网格中挑出某一列单元转移到其他进程上，需要使用数组标记每个单元格所在的列，当执行负载转移时，遍历标记数组，从中挑出所需的单元格，并放入一块连续的数组中。为了避免这种方式带来的麻烦，改为修改非结构网格的存储方式，将整个网格存储地址以列为单位进行划分，如图8 所示，各列分别占据一块连续的空间，与图7 相同，2 号单元格加密，其所在列的任何单元格的增加和变动都在这一块空间中，要转移第一列（1，3，10，11，12，13 号单元格）不需挑选，直接转移即可。这使得以列为单位的负载转移成为可能，并且程序在执行时有较高的空间局部性。

图8 以列为单位的存储方式

4.4 负载转移策略

本文采用的转移策略为进程一对一进行负载转移，这种迁移是一种简单易行的方法，在其基础上可以实现更为复杂的迁移策略。

负载平衡分为两个阶段：

负载转移过程：将进程按照预测的负载大小排序，负载转移的规则为最大负载的进程转移给最小负载的进程，次大负载的进程转移给次小负载的进程，以此类推。在过载进程（即进程负载大于平均负载）的内部，负载以列为单位进行排序，要转移的负载为从最大负载列开始，隔列转移。这样做的原因是由于燃烧的稳定性使得相邻网格列上的负载接近，通过排序并隔行转移可以使得转移的源进程与目的进程的负载相近，避免过多或过少转移负载，引入新的负载不平衡。主控进程标记转移的方向及数量，并广播给所有计算进程。然后根据上一步收到的标记数组，负载小于平均负载的进程（欠载进程）准备接收数组，并扩大计算涉及的输入及输出数组，从过载进程接收计算需要的输入数组包，拆包将数据放入适当的位置；过载进程准备发送数组，将计算需要的输入数组打包，并发送给对应的欠载进程。

在计算完成之后，原来的欠载进程将计算后改变的输出数组打包，发送给原来的过载进程。并恢复计算涉及的输入及输出数组为原来的规模。原来的过载进程准备接受数组包，并将其放入原先的位置。

5 效果的评价

本文从每一个计算步中，进程的负载统计、有负载平衡策略与无负载平衡策略时程序的运行时间、进程之间的负载不平衡程度等方面对负载平衡的策略进行分析。

（1）负载不平衡程度的改善

由于所有进程中负载最大的进程执行时间最长，直接影响到程序执行的总时间；而平均负载是理想情况下每个进程的执行时间。

有负载转移和无负载转移时，最大负载与平均负载的比值如图9 所示，横轴为程序执行的步骤，灰色实线为无负载转移时最大负载与平均负载的比值，虚线部分为使用牛顿迭代次数预测负载策略时最大负载与平均负载的比值，黑色实线部分为结合两种预测方式后最大负载与平均负载的比值。从图中可以看出，使用牛顿迭代次数预测在绝大部分时间可以较好地降低最大负载与平均负载的比值，但是在400 步左右由于化学反应剧烈，这种策略就不够有效。加入放热量Q 预测负载后，在化学反应剧烈的阶段也能很好地预测负载变动趋势，最大负载与平均负载的比值降低到无负载转移的一半左右。

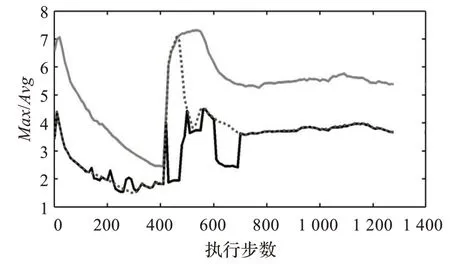
图9 最大负载与平均负载的比值

有负载转移和无负载转移时，各进程的负载如图10所示。

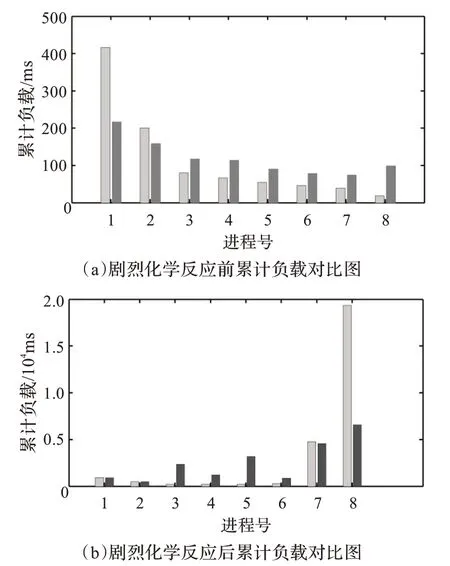
图10 不同燃烧阶段进程上的负载对比

图10的横轴为各进程编号，纵轴为该阶段的累计负载，浅色直方图为无负载转移的统计负载，深色直方图为有负载转移的累计负载。图10（a）显示了剧烈化学反应开始之前，在各进程上无负载转移和有负载转移的负载，有负载转移的部分负载更为平均。图10（b）显示了剧烈化学反应开始之后，无负载转移和有负载转移的负载累计，有负载转移的部分仍然更为平均。从图10 还可以看出，有负载转移的最大负载接近无负载转移的最大负载的一半，进程间的负载在有负载转移时更加平衡。

（2）负载转移时间分析

为了使负载转移有效地执行，即负载转移的开销不能大于负载转移带来的性能提升，因此需要度量负载转移带来的开销。

由于每一个迭代步中，影响程序执行时间的部分为负载最大的进程的执行之间，因此使用每个迭代步负载最大的进程中，负载转移开销占总的求解常微分方程计算时间的比值作为负载转移的开销。如图11 所示。

图11 负载转移所占时间比例

由图11 中可以看出，负载转移所占时间比例最大不超过总执行时间的35%，而根据负载转移策略，是将过载进程与欠载进程负载差值的一半转移出去，即计算时间的50%，即节省了50%的时间，而最大的开销仅为30%，特别是剧烈化学反应负载比较大的情况下，负载转移策略的开销不到计算时间的5%，由此可以得出负载转移一定是有效的。

（3）程序总体性能的提升

为了分析负载转移策略对主程序带来的性能提升，需要分析求解常微分方程计算部分占整个程序运行时间的百分比。经过实验得出，在程序的核心计算过程中，解常微分方程计算时间占总执行时间的5%～35%。

定义性能提升的度量为在并行情况下，不同核数执行程序核心计算过程时，和有负载平衡的执行时间与无负载平衡的执行时间减少时间的比值。测试网格初始时为24×4，化学反应稳定时的规模在30 000 左右。

从表1中可以看出，程序的核心计算性能总体随着核数的增加而提高，12 核运行时程序性能提升达到了10.20%。

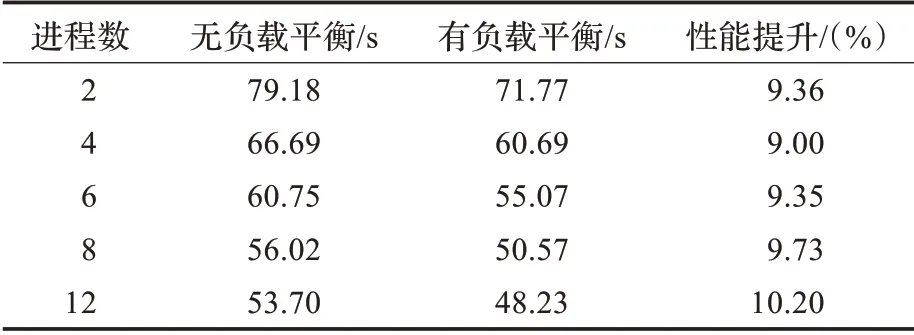
表1 程序的性能提升

6 总结和未来工作

本文对非结构网格自适应的燃烧并行数值模拟计算的特点进行了详细的研究，提出了数据按列存储的改进方式和根据不同化学反应情况预测负载的机制，还提出了将负载一对一地转移到欠载进程上动态负载平衡策略，将最大负载与平均负载的比值降低了一半左右，程序总体性能提升在9.00%～10.20%。由于一对一负载转移的限制，还有部分进程处于空闲状态，下一步的工作是将负载转移改为一对多，将过载进程上的负载尽可能多地分出去，使得所有进程上的负载更加平衡。

[1] Chen Z，Burke M P，Ju Y.Effects of compression and stretch on the determination of laminar flame speeds using propagating spherical flames[J].Combustion Theory and Modelling，2009，13（2）：343-364.

[2] Sun，Takayama.Conservative smoothing on an adaptive quadrilateral grid[J].Journal of Computational Physics，1999，150（1）：143-180.

[3] Hummel S F，Schonberg E，Flynn L E.Factoring：a method for scheduling parallel loops[J].Comm of the ACM，1992，35（8）：90-101.

[4] Kumar V，Grama A Y，RaoVempaty N.Scalable load balancing techniques for parallel computers[J].J of Parallel and Distr，1994，22（1）：60-79.

[5] Lain M S，Rothberg E E，Wolf M E.The cache performance and optimizations of block algorithms[C]//4th Int Conf on Architectural Support for Progr Lang and Operating Systems，1991：63-74.

[6] Orlando S，Perego R.A template for non-uniform parallel loops based on dynamic scheduling and prefetching techniques[C]//Proc of the 1996 ACM Int Conf on Supercomputing，1996：117-124.

[7] Orlando S，Perego H.SUPPLE：an efficient run-time support for non-uniform parallel loops[J].J of System Architecture，1999，45（15）：1323-1343.

[8] Oliker L，Biswas R.PLUM：Parallel Load balancing for adaptive Unstructured Meshes[J].Parallel and Distributed Computing，1998，52（2）：150-177.

[9] Bui T.Graph bisection algorithms with good average behavior[J].Combinatorica，1984，7（2）：181-191.

[10] Kernighan B，Lin S.An efficient heuristic procedure for partitioning graphs[J].Bell System Technical Journal，1970，49（2）：291-307.

[11] Chan T，Mathew T.Domain decomposition algorithms[J].Acta Numerica，1994，3（1）：61-143.

[12] 王学德，伍贻兆，夏健.动态负载平衡的二维非结构网格DSMC并行算法研究[J].空气动力学学报，2007，25（3）：339-361.

[13] 刘鑫，陆林生，陈德训.非结构网格并行计算预处理方法研究[J].计算机科学，2012，39（3）：308-311.

[14] 陈建军.非结构网格的并行划分和自适应非结构化网格生成及其并行化的若干问题研究[D].杭州：浙江大学，2006.

[15] 李桂波，杨国伟.基于多块结构网格的并行计算及负载平衡研究[J].宇航学报，2011，32（6）：1224-1230.