基于改进Mean Shift和SURF 的目标跟踪

包 旭，杜 凯，田 浩

1.淮阴工学院 交通工程学院，江苏 淮安223003

2.长安大学 电子与控制工程学院，西安710064

1 引言

运动对象跟踪是计算机视觉领域的一个重要研究方向，在视频监控、机器人导航、自动驾驶、交通流量监测、天文观测、视频图像压缩和传输等方面都有广泛的应用。Mean Shift 最初作为一种聚类分析的方法由K.Fukunaga等人提出[1]。Yizong Cheng 等人对Mean Shift 算法进行推广[2]。Dorin Comaniciu 等人将Mean Shift引入到目标跟踪算法中，提出了基于核（Kernel-based）的跟踪算法[3-4]。

基于核的跟踪算法使用目标的归一化加权颜色直方图作为目标模式。由于颜色直方图是目标的整体统计特征，没有包含目标的空间信息，当目标和背景颜色分布相近时，容易导致不准确跟踪或跟踪丢失。文献[5]采用内中外三层的分块方法，空间信息结合颜色信息，生成空间颜色直方图，各块采用等权值法加权处理。文献[6]采用上下二分的分块方法跟踪曲棍运动员，这种分块方法适合于柱状对象。文献[7]提出了7 部分的分法，各块Bhattacharyya系数采用了算法平均值的方法，没有考虑各块相似度的变化对总体相似度的不同影响。文献[8]在文献[7]的基础上，结合人体特征，提出了适合人体的分块方法，且各块采用非等权值的方法加权处理。文献[9]提出了显著性加权的方法，根据目标中不同区域与背景的差别大小，赋予不同区域不同的权值。由于SURF、SIFT 等特征具有旋转、尺度不变性，对三维视角、光照变化具有很强的适应性，在遮挡和场景混乱时仍保持不变性等优势[10-12]，文献[13]在MS 跟踪结果的基础上，采用SIFT 特征匹配寻找SIFT 匹配点集，通过计算仿射变换参数修正MS 跟踪结果。文献[14]结合颜色特征和SIFT 特征，通过MS 算法迭代，采用EM 框架寻找最相似区域，实现跟踪。文献[15]引入仿射变换，采用Bhattacharyya 系数将目标跟踪问题转化成仿射变换参数的最优化问题，实际中取得了不错的跟踪效果，但耗时较长。文献[16]中提出了自适应分块颜色直方图的跟踪算法，该算法能较好地解决部分遮挡、目标对象矩形变化时的跟踪问题，但在光照变化和快速运动的情况下，跟踪效果未能得到明显提高。

受文献[4-13，16]启发，本文提出一种融合改进MS 和SURF 的跟踪算法，该方法由改进的Mean Shift 跟踪算法（初定位）和SURF 特征匹配和校正（微调）组成。前者根据目标对象的最新外接矩形尺寸，确定对象的分块方法，根据各块的相似度大小，确定各块的权重系数；后者在前者跟踪结果的基础上，采用SURF 特征匹配和校正。最后，通过线性加权的方法融合改进MS 和SURF 的跟踪结果。实验表明，本文算法在目标发生旋转、尺度变化、光照变化和部分遮挡等情况下，都有很好的跟踪效果。

2 改进的Mean Shift跟踪算法

与传统的MS 跟踪算法[3-4]相比，改进的MS 算法主要由自适应分块方法和加权Bhattacharyya系数组成。

2.1 自适应分块方法

不同的运动对象常常具有不同的外观尺寸，同一运动对象也会随着运动的变化而发生方位和尺寸上的变化。因此，固定尺度和固定分块的方法常常不能满足变化的、复杂的情况。基于此，本文采用自适应的分块方法，自适应分块对于运动目标跟踪的实验效果，参见文献[16]。

假设包围运动对象的外接矩形如图1 所示。矩形的宽度为w，高度为h，定义目标对象宽度/高度比例因子k ，k=w/h，k 反映了目标对象外接矩形的外形特征，当k ＞1 时，外接矩形呈现“宽矩形”；当k=1 时，外接矩形为“正方形”；当k ＜1时，外接矩形呈现“窄矩形”；则k 有式（1）三种情况。

图1 目标对象的外接矩形

考虑到实际运动中，目标对象外接矩形常常处于“宽矩形”和“窄矩形”两种状态，正方形仅是动态目标对象外接矩形的临界状态，故此，结合文献[1，3，6]的分块方法和实验的需要，本文取参数kc为2，将目标对象划分为三种不同类型的分块方式，如图2 所示。

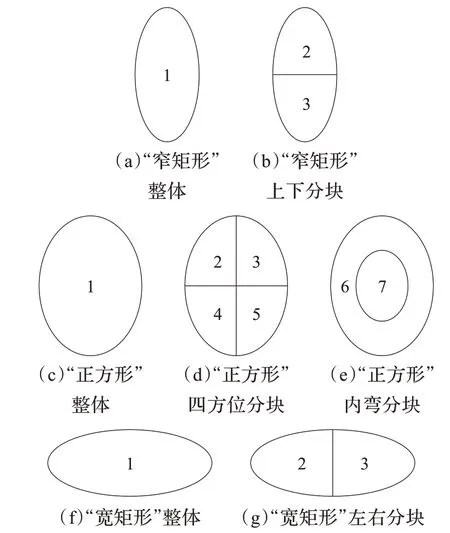
图2 自适应分块方法

2.2 加权Bhattacharyya 系数

Bhattacharyya 系数用来衡量目标模式和候选目标模式的相似程度。文献[7]中Bhattacharyya 系数采用了平均值的方法，没有考虑各块相似度的变化对整体相似度的不同影响。借鉴文献[8-9]中各块加权处理的思想，本文根据各块的Bhattacharyya 系数的大小，相似度大的块，权重系数大，相似度小的，权重系数小。按照式（2）对各块进行加权处理，各块的权值由式（3）确定。

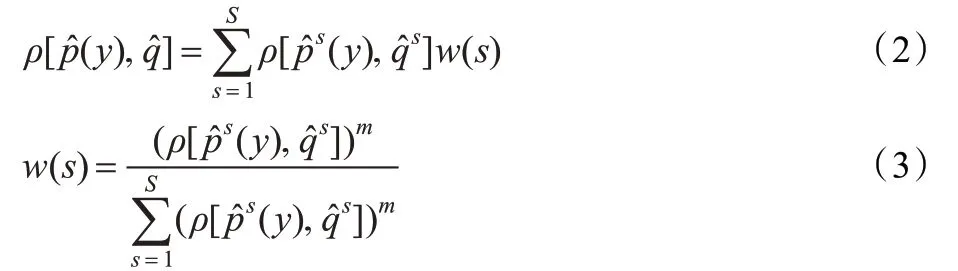
2.3 改进的Mean Shift算法步骤

初始第一帧，设当前目标对象外接矩形的尺寸为w0×h0，矩形中心为，计算宽度/高度比例因子k0=w0/h0，根据式（1）确定初始目标对象的分块方法，总的分块数记为S。根据文献[3]中式（21）计算目标模板的直方图s=1,2,…,S 。

步骤1读取下一帧图像，计算该帧图像位置候选目标的直方图，s=1,2,…,S，并计算

步骤2采用文献[3]中式（25）计算{wi},i=1,2,…,Np，其中和取整块的特征情况。

步骤3采用文献[3]中式（14）计算新的迭代位置，本文采用的是Epanechnikov 核函数。

步骤4计算位置候选目标的直方图2,…,S，计算

步骤5如果，则

步骤6若＜ε，执行步骤7；否则，，执行步骤2。

步骤7根据当前目标对象外接矩形尺寸w×h，计算宽度/高度比例因子k=w/h，根据式（1）确定运动对象的分块方法，总的分块数记为S，执行步骤1。

3 融合改进Mean Shift和SURF 的跟踪算法

融合改进Mean Shift 和SURF 的跟踪算法由改进的Mean Shift（初定位）和SURF 特征匹配和校正（微调）组成，最终跟踪结果由两部分线性加权获得。其改进的MS 算法如上文1 章描述；SURF 特征匹配和校正（微调）由SURF 特征提取、SURF 特征匹配、特征点重心位移偏移量计算和跟踪结果校正四部分组成。其算法流程如图3 所示。

图3 融合改进的MS 和SURF 的跟踪算法流程

3.1 SURF 特征提取

SURF（Speed Up Robust Features）特征是由Bay 等人[11-12]提出，借鉴了SIFT 简化近似的思想，对DoH 高斯二阶模板进行简化近似处理，使得模板对图像的滤波只需要进行简单的加减法运算，又因为采用积分图像的方法，其运算时间与滤波模板的尺寸无关。实验表明，SURF 算法的运算速度是SIFT 的3 倍，综合性能优于SIFT 算法，其详细的算法详见文献[11-12]。

3.2 SURF 特征匹配

SURF 特征匹配采用特征点向量间的欧式距离作为相似性度量。设目标区中某个特征点向量为Va，找出与其MeanShift 跟踪结果（待校正区）中欧式距离最近的前2 个关键点向量Vb和Vc，如满足式（4），则接受该对匹配点，否则去除。其中t是一个给定的阈值，取为0.8[10]。

3.3 特征点重心偏移量计算

经过2.2 节SURF 特征匹配，目标区和待校正区对应的特征点集分别为P={(xi,yi),Vi}，i=1,2,…,N和P′={(x′i,y′i),V′i}，i=1,2,…,N。本文采用平均值的方法，计算待校正区对象相对于目标区对象的重心平均偏移量，如式（5）所示。

3.4 改进的MS 跟踪结果校正

设改进的MS 算法的跟踪结果为：

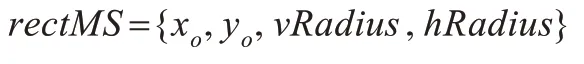
其中(xo,yo)表示矩形跟踪区域的中心坐标，vRadius表示矩形垂直方向的半径，hRadius表示跟踪矩形水平方向的半径。结合公式（5），校正后的结果如式（6）所示，其中rectSURF表示SURF 匹配和校正后的跟踪结果。

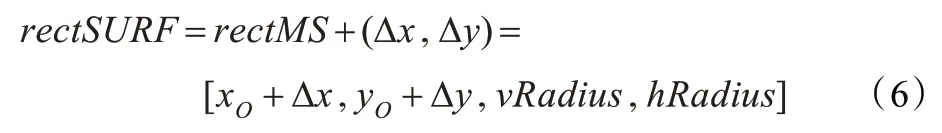
3.5 融合改进MS 和SURF 的跟踪结果

融合改进MS和SURF跟踪结果为rect，如公式（7）所示。

α为权值系数，介于0～1 之间，当改进的MS 算法Bhattacharyya 值较大时，则MS 算法跟踪结果较好，此时α取较大值；反之，α取较小值。实验中，为了简化融合算法的计算难度，本文α参数取为0.5，更进一步的自适应调节α参数的取值方法，有待于在后续研究中展开。

4 实验与分析

本文实验采用Epanechnikov 核，RGB 各子空间采用16个bin，共使用16×16×16 个bin，每帧图像的最大迭代次数设为10 次，实验视频数据简要描述如表1 所示。

表1 实验视频数据简要描述

4.1 改进的Mean Shift算法初步跟踪

“PETS2006S2-T3-C4”序列#784 帧图像，人体受到他人遮挡，文献[4]算法调整自身尺度，顺利实现跟踪，但跟踪大小小于对象实际大小，如图4（a1）所示；文献[7]算法跟踪大小基本保持与对象大小相同，但跟踪中心与对象实际中心有较大偏差，如图4（b1）所示；而本文提出的改进的MS算法采用加权Bhattacharyya 系数法，受遮挡的块相似度较小，其对应的权重系数较小，未遮挡块相似度较大，其权重系数较大，有效地削弱了受遮挡块对整体相似度的影响，保持了与对象相同的大小，跟踪中心与对象实际中心也较好地吻合，如图4（c1）所示。

图4 改进的Mean Shift算法与文献[4]、文献[7]算法在发生遮挡，复杂背景，光照变化和仿射变换情况下的跟踪性能对比

“OneBagBoy.avi”视频#3 057 帧图像，人体裤子的颜色与背景车辆颜色相同，文献[4]算法只考虑了整体区域颜色的统计信息，没有考虑空间信息，所以跟踪结果出现较大偏差，跟踪结果向上偏移，如图4（a2）；文献[7]算法采用图2（c）～（e）的分块方法，其跟踪大小基本保持与对象大小相同，但因各块取平均值的方法，其跟踪中心与对象实际中心存在一定偏差，如图4（b2）；而本文提出的改进的MS 算法根据人体外接矩形尺寸，采用上下二分的方法，有效地避免了文献[4]向上偏移的跟踪结果，且因为采用加权Bhattacharyya 系数的方法，有效地保证了改进的MS 算法跟踪中心与对象实际中心较好地吻合，如图4（b3）。

“DavidIndoor.avi”视频#755 帧图像，人脸发生光照变化，可以看出，文献[4，7]和改进的MS 算法均存在不同程度的跟踪精度或跟踪丢失，分别如图4（a3）、（b3）、（c3）。

4.2 SURF 特征匹配和校正

（1）SURF 特征匹配和特征点重心偏移量计算

在改进的MS 算法跟踪结果的基础上，提取待校正区的SURF 特征，作目标区和待校正区的SURF 特征匹配，其匹配效果如图5 所示。右侧图内部蓝色矩形为改进的MS算法的跟踪结果，考虑到改进的MS 算法跟踪结果（待校正区）与实际的对象有位置上的偏移，实验中，将待校正区扩大0.5 倍，即右侧图外部虚线的矩形区域，保证搜索区中包含目标对象，以增加匹配的鲁棒性。

（2）本文算法与文献[4]和文献[14]的跟踪性能比较

表2 是文献[4]，文献[14]与本文跟踪算法平均跟踪误差（均值±标准差）和跟踪时间的比较结果。图6（a1）～（a3）是文献[4]算法的跟踪结果；图6（b1）～（b3）是文献[14]算法的跟踪结果；图6（c1）～（c3）是本文算法的跟踪结果。

图5 SURF 特征匹配和特征点重心偏移量计算

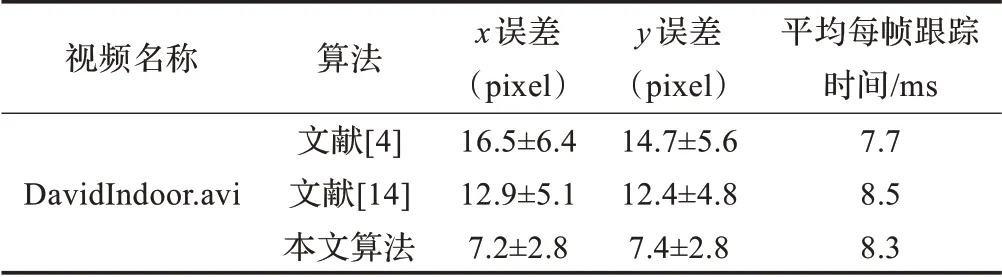
表2 平均跟踪误差（均值±标准差）和跟踪时间比较

图6 本文算法与文献[4]、文献[14]算法在光照变化情况下的跟踪性能对比

由表2 可以看出，在“DavidIndoor.avi”视频序列中本文算法的误差是最小的，跟踪时间略高于文献[4]，但低于文献[14]。由图6 可以看出，文献[4]算法在视频#475、#635 和#830帧均产生跟踪漂移；文献[14]采用Mean Shift融合SIFT的算法，在视频#91 和#162 帧都能成功跟踪，但由于整体框架仍是Mean Shift 算法，故而仍存在一定偏差；而本文算法由于采用改进的MS 算法初步定位，采用SURF 匹配、校正对其MS 结果进行微调，之后融合MS 和SURF 结果，故而在#475、#635 和#830 帧都能准确地跟踪。

5 结束语

本文提出了一种融合改进MS 和SURF 的跟踪算法，改进的MS 算法能根据目标对象的最新外接矩形尺寸确定对象分块方法，根据各块的Bhattacharyya 系数值，确定各块的权重系数；在改进的MS 跟踪结果的基础上，采用SURF匹配和校正获得校正跟踪结果；最后，对两结果进行线性加权，获得最终的跟踪结果。实验表明，本文算法可以有效地跟踪部分遮挡、复杂背景、光照变换和仿射变换情况下目标对象，改善了传统MS 算法和固定分块MS 算法的局限性，提高了跟踪算法的鲁棒性。

[1] Fukunaga K，Hostetler L D.The estimation of the gradient of a density function，with applications in pattern recognition[J].IEEE Trans on Information Theory，1975，21（1）：32-40.

[2] Cheng Y.Mean Shift，mode seeking，and clustering[J].IEEE Trans on Pattern Analysis and Machine Intelligence，1995，17（8）：790-799.

[3] Comaniciu D，Ramesh V，Meer P.Real-time tracking of nonrigid objects using Mean Shift[C]//Proc of IEEE Conf on CVPR，2000：142-149.

[4] Comaniciu D，Ramesh V，Meer P.Kernel-based object tracking[J].IEEE Trans on Pattern Analysis and Machine Intelligence，2003，25（5）：564-575.

[5] Xu D，Wang Y，An J.Applying a new spatial color histogram in Mean-Shift based tracking algorithm[C]//Image and Vision Computing，New Zealand，2005.

[6] Okuma K，Taleghani A，De Freitas N，et al.A boosted particle filter：multitarget detection and tracking[C]//Proc of the European Conference on Computer Vision，2004：28-39.

[7] Maggio E，Cavallaro A.Multi-part target representation for color tracking[C]//Proc of IEEE Int Conference on Image Processing（ICIP），2005：729-732.

[8] 袁霄，王丽萍.基于MeanShift 算法的运动人体跟踪[J].计算机工程与科学，2008，30（4）：46-49.

[9] 张恒，李由，李立春，等.基于显著性加权的Mean Shift 跟踪方法[J].光学技术，2008，34（3）：404-407.

[10] Lowe D G.Distinctive image features from scale-invariant keypoints[J].International Journal of Computer Vision，2004，60（2）：91-110.

[11] Bay H，Tuytelaars T，van Gool L V.SURF：Speeded Up Robust Features[C]//ECCV，2006.

[12] Bay H，Tuytelaars T，Gool L V.SURF：Speeded Up Robust Features[J].Computer Vision and Image Understanding，2008，110（3）：346-359.

[13] Chen A H，Zhu M，Wang Y H.Mean Shift tracking combining SIFT[C]//Proc of ICSP’08，2008：1532-1535.

[14] Zhou H Y，Yuan Y，Shi C.Object tracking using SIFT features and Mean Shift[J].Computer Vision and Image Understanding，2009，113（3）：345-352.

[15] 李培华，肖莉娟.基于Mean Shift的相似性变换和仿射变换目标跟踪算法[J].中国图象图形学报，2011，16（2）：258-266.

[16] 杜凯，巨永锋，靳引利，等.自适应分块颜色直方图的Mean-Shift跟踪算法[J].武汉理工大学学报，2012，34（6）：140-144.