融合过抽样和欠抽样的不平衡数据重抽样方法
吴 磊,房 斌,刁丽萍,陈 静,谢娜娜
1.重庆大学 计算机学院,重庆400030
2.第三军医大学新桥医院 健康管理科,重庆400037
1 引言
近几年来,数据挖掘和机器学习等领域的快速发展和面向数据挖掘的软件的开发和不断完善更新(如文献[1-2]提到的weka),以及诸多学者对不平衡数据集分类的深入研究。在对不平衡数据集分类的研究中,样本数很少的类往往更会受到关注,比如疾病诊断、体检数据敏感信息挖掘、网络入侵、敏感信息检索和信用卡欺诈检测等。上述这些事件的检测对社会来讲意义重大,所以对不平衡数据的分类就显得尤为重要。软件缺陷预测是典型的数据不平衡应用问题,从软件模块中抽取特征向量,通过分类器判断软件模块有无缺陷,本文使用了包括开放的NASA MDP数据库[3]和来自PROMIS 的AR 数据库[4]中的总共12 个数据集,并且使用了一些早期的预处理方法和分类器后,实验结果显示某些重采样方法带来的效果并不理想,所以需要寻找更好的算法来对不平衡数据进行分类。
处理数据不平衡问题的方法主要有两大类:数据抽样方法和代价敏感学习算法,本文研究了抽样方法的改进。数据抽样算法有两类:过抽样和欠抽样。常用的抽样方法有随机向上采样(过抽样)、随机向下采样(欠抽样)、压缩最近邻(CNN)[5-6]、邻域清理(NCL)、虚拟少数类向上采样(SMOTE)[7]、Borderline-SMOTE(BSM)[8]、one-sided selection(OSS)、Cluster-Based Oversampling(CBOS)等。还有一些组合的方法,如Gustavo 等人提出的SMOTE+ENN 和SMOTE+Tomek[9]。
本文主要研究了过抽样和欠抽样相结合的方法,使用BSM、CBOS 分别和Tomek links 及ENN 结合,即BSM+Tomek、BSM+ENN、CBOS+Tomek 和CBOS+ENN;研究这几种组合算法是因为对于样本数较少的数据集,进行单纯的过抽样和欠抽样会带来不好的影响,过抽样会使样本数极少的数据集中的小类过度拟合,而欠抽样会使得样本数本来就比较少的数据集丢失重要的样本,组合方法能够比较折中地处理这两种问题;其次,已有学者如Gustavo 等人提出过抽样和欠抽样结合的方法,并表现出了良好的效果,本文试图通过研究这几种组合方法来发掘它们的潜能;第三,这几种算法在单独执行时就表现出了较好的效果,希望通过对其进行组合来发掘更好的抽样方法;第四,暂时没有文献对这几种算法进行组合和分析。
本文在预处理阶段采用了14 种采样方法,其中包括本文提出的四种方法对不平衡数据进行分类,并且使用了12种不同不平衡度的数据集和11 种分类器(训练过程采用了10-交叉验证)做比较实验,期间使用了weka 软件做了一系列实验分析,评价标准为areaUnderROC(AUC),最后给出各算法预处理后的分类结果以及实验结论。
2 不平衡数据的分类器训练
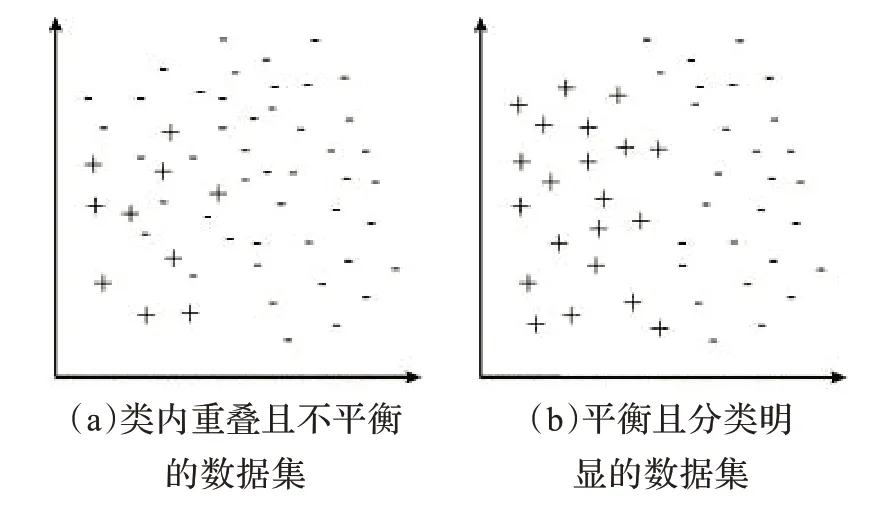
图1 两种数据集的比较
在机器学习和数据挖掘的研究中,不平衡数据集往往表现为各类数据极度不平衡、小类和大类重叠等现象,所以使用不平衡数据训练分类器变得十分困难,这便导致对不平衡数据集的分类也变得非常困难。为了更好地说明问题,文中引用了图1,其中图1(a)中有两个在一定程度上重叠的极为不平衡的类:大类用“-”表示,小类用“+”表示。图1(b)中则是两个平衡且分类明确的两个类。很显然,图1(b)更便于训练分类器,本文的目的就是通过对数据进行预处理将图1(a)中的不便于训练分类器的不平衡数据转成图1(b)中适合训练学习的平衡数据。
小类中的一些样本往往会导致一些像K近邻之类的分类器的分类效果变差。比如由于小类中的某些样本的最近邻样本属于大类,所以会错分小类中的许多样本。在不平衡度很高的数据集中,小类的样本的最近邻是大类中样本的概率可能很大,并且分类结果中把小类分错的概率高到不可接受。
3 评价标准
基于混淆矩阵分析的方法是评价一个分类器性能好坏的最直接的方法。
因为多分类问题通常可以简化为两类问题来解决,所以不平衡数据集的分类问题的研究重点是提高两类问题中少数类的分类性能。当使用一般的分类精度准则时,虽然能够体现出整体数据的分类性能,但是它不能正确地评价不平衡数据集的分类结果。这是因为当多数类样本比少数类样本多得多的情况下,分类器把所有的样本都分类为多数类,此时它的分类精度仍然很高,比如上述的信用卡欺诈问题中,但此时的分类没有任何的价值,因为少数类样本的识别率为零。也就是说在使用一般的分类精度准则时,少数类样本对分类精度的影响小于多数类样本,所以用一般的分类精度准则显然是不合适的。因此应当要选择一个合适的准则,使分类器在其分类性能上能体现出少数类样本的影响。不平衡数据集分类问题中常用的评价准则有:F-values、G-Means、ROC 曲线[10]、F-Measure等。F-values 和G-Means 都是在两类的数据集的混合矩阵的基础上提出来的。本文主要使用了areaUnderROC 和F-Measure。
首先了解一下ROC曲线,也称受试者工作特性(Receiver Operating Characteristic,ROC)曲线,独立于数据集类间的分布,对数据集的不平衡性有很好的鲁棒性,因此可用于不平衡数据集分类器性能的评价。ROC 曲线图纵轴表示真实确定率:TP rate=TP/正例数;横轴表示虚假确定率:FP rate=FP/负例数。ROC 曲线有效地反映了在分类器参数变换时,真实确定率(TP rate)与虚假确定率(FP rate)之间的变化关系。坐标中的(1,1)点对应于将所有点归于正类;直线y=x对应于随机猜测;(0,0)点对应于将所有点归于负类;(0,1)点对应于最理想的分类情况,即所有样本均分类正确。曲线越靠近左上角,分类器性能越好。由于ROC曲线没有给出具体的数值,所以不方便评价不同分类器间性能的优劣,于是常使用ROC 曲线下的面积(Area Under ROC,AUC)作为评价指标。显然,较大的AUC值对应于较优的分类器。AUC是基于ROC 曲线的唯一数值,它与错分代价无关,不受与规则应用相关的因素的影响。本文使用了Weka 软件中的AUC值的估计方法,在后面的实验结果里给出了具体的数值。
4 算法
处理不平衡数据集分类的方法主要可分为两大类:数据抽样方法和代价敏感分类算法。代价敏感分类算法主要是通过改进传统的分类算法,提出新的分类思想。例如,传统的Boosting 算法在处理不平衡数据集时效果不佳,没有考虑到不平衡数据集的情况,正分样本所减少的权重与错分样本所增加的权重比例是相同的,所以文献[11]提出的基于Boosting 的支持向量机算法针对不平衡数据分类得到较好的效果。文献[12]提出了一种针对医学数据的不平衡数据的学习算法。数据抽样方法主要有随机向上采样、随机向下采样、压缩最近邻(CNN)、邻域清理(NCL)、虚拟少数类向上采样(SMOTE)等,这里着重介绍以下几种:
(1)Tomek links
该方法的基本思想如下:给定两个样本(xi,xj)属于不同的类,它们之间的距离用d(xi,xj)表示。若不存在另一样本x满足d(xi,x)<d(xi,xj)或d(x,xj)<d(xi,xj),则样本对构成一个Tomek links。如果两个样本构成Tomek links,则其中某个样本为噪点,或者两个样本在两类的边界上。利用这个性质,Tomek links 可作为欠抽样的方法,即去掉构成Tomek links的负例。
(2)Edited Nearest Neighbor(ENN)
ENN的基本思想是去掉那些类标与离它最近的三个样本中的两个类标不同的样本。但多数类的样本附近通常都是多数类的样本,因此ENN 去掉的样本是非常有限的。
(3)Cluster-Based Oversampling(CBOS)
CBOS抽样方法不仅仅考虑到类间不平衡的处理,而且还考虑到了类内不平衡的处理。首先采用k-means 对训练数据集进行聚类;然后使用随机过抽样对大类和小类中的所有cluster进一步聚类,对于大类,除了最大的那个cluster,都要进行进一步聚类直到所有的cluster中的样本数量与最大的那个cluster 一样多;对于小类,对每一个cluster 随机过抽样直到每一个cluster中包含max_classized/Nsmallclass个样本,其中Nsmallclass代表小类中的cluster数目。
(4)Borderline-SMOTE(BSM)
BSM 是基于SMOTE 的数据抽样算法,与其他抽样方法不同的是,只对小类的边缘样本做过抽样,并不是对小类中所有样本进行过抽样。具体算法如下:首先,找出小类中的边缘样本;然后,利用这些边缘样本产生人造样本并将其加入到原始训练样本中。假设整个训练数据集是T,小类是P,大类是N,pnum和nnum分别是小类和大类的样本数。对小类中的每一个样本pi,计算它与整个数据集T中所有样本的m近邻,m近邻中大类样本的数量取决于m1(0 <m1<m)。如果m1=m,pi中的所有m近邻都是大类样本,pi就被认为是噪声数据不会参加下面的算法;如果,0 ≤m1≤m/2,pi是正确的并且也不会参与下面的算法;如果m/2 ≤m1≤m,pi的最近邻中,大类样本数量多于小类,pi就被认为是误分并且被放入数据集DANGER 中;然后得到一个数据集DANGER(假定有dnum个样本),也就是小类P的边缘数据,对于DANGER 中的每一个样本pii计算它与小类P中样本pi的K近邻,从中随机选择s个近邻计算它们与pii的欧氏距离dif,然后通过公式:syntheticj=pii+rj×difj产生s个新的小类样本,总共产生s×dnum个人造样本赋给小类。
以上是基于数据抽样的几种处理不平衡数据的基本方法。近几年专家们针对这些基本方法的不足提出了许多改进的新方法。Gustavo 等人将过抽样和欠抽样方法结合提出SMOTE+Tomek 和SMOTE+ENN 方法;Taeho 等人提出基于聚类的向上采样方法,可同时处理类间和类内不平衡。
Gustavo 等人将过抽样与欠抽样方法进行组合取得了比较好的效果,但是对其他算法的组合暂时没有文献给出详细的研究,所以本文就BSM 和CBOS 与Tomek 和ENN 进行组合并验证这种组合的可行性。通过本文的工作发现这种组合是可行且有效的,有意义的;本文通过对BSM 和CBOS 进行清洗,提出了四种过抽样和欠抽样算法结合的方法:首先通过BSM 对数据集进行过抽样,然后分别运用Tomek links 和ENN 对数据集进行欠抽样得到两种抽样方法:BSM+Tomek,BSM+ENN;同理,通过CBOS对数据集进行过抽样后,使用Tomek links 和ENN 对数据集进行欠抽样,得到两种抽样方法:CBOS+Tomek,CBOS+ENN。
通过实验结果发现,这四种抽样方法在大多数实验所用数据集和分类器下效果比不做数据清洗好,在某些情况下,效果不是很理想,这取决于要使用的数据集以及分类方法,当然评价标准的不同也会引起实验结果的差异,本文将在后面的实验结果分析中给出详细介绍。
5 实验
5.1 实验设计
实验使用了14 种数据抽样方法,包括本文提出的四种抽样方法;使用了12 个不平衡数据集(表1),为了便于统计比较,使用了仅有两类的数据集;为了更好地说明数据抽样方法的不同对不平衡数据集分类的影响,文中使用了11种不同的分类器进行实验,并且在训练分类器时使用了10-交叉验证,来处理由于数据集过小可能产生的影响。这里选择使用了12 个常用的软件缺陷数据库,软件缺陷预测是典型的数据不平衡应用问题,从软件模块中抽取出特征向量,通过分类器判断软件模块有无缺陷,属于二分类问题。本文选择的软件缺陷数据库来自NASA MDP 数据库和PROMIS 的AR 数据库中的数据集,进行对比实验。表1中对12 个数据集的属性进行了对比分析,Obj 表示数据集的属性,DS 代表数据集(Data Set),Examples 表示数据集中样本数量,Atrribues 中表示数据集有多少属性,文献[13]中提出,数据集的不平衡度不同,分类的效果也将有所差异,所以本文使用了不平衡度有差异的数据集,其中class(%)表示小类占数据集的比例(即不平衡度)。

表1 数据集
本文采用的实验环境是:MATLAB R2007a 以及weka3.5.8,实验环境为Pentium®Dual-Core CPU E5200 2.50 GHz,2 048 MB,Windows XP,其中还调用了weka 的接口来使用weka 自带的分类方法和评价方法。实验步骤为:实验中采用十字交叉验证法。实验使用了14 种数据抽样方法,包括本文提出的4 种抽样方法;12 个不平衡数据集(表1)。为了便于统计比较,采用仅有两类的数据集(二分类问题),并选择11 种不同的分类器进行实验;这样就得到了一个三维表,不同的数据集,不同的采样方法和不同的分类器。为了使表格更加直观明了,文中对此表格做出了简化,分别将抽样方法和分类器对应的AUC值求平均值,得到两个二维表,也就是在不同数据集下使用不同的重采样方法之后进行分类,每一个数据集在每一个采样方法下使用11 种分类器后得到了11 个AUC值,将得到的AUC值求平均得到了每一个数据集在每一个采样方法下进行分类后得到的AUC值,也就是表2 中看到的数据,这里研究采样方法对不平衡数据分类的影响;同理,对于某一个数据集使用14 种采样方法,进而使用某一个分类器得到的14 个AUC值,将这些采样方法对应的AUC值求平均就得到在某一数据集下使用某一分类器得到的AUC值,也就是表3 中的数据,这里研究分类器对不平衡数据分类的影响。
5.2 结果与分析
通过一系列对比实验发现,本文提出的四种组合方法在多数情况下优于原抽样方法,表2 中的行代表不同的软件缺陷数据集,列代表不同的重抽样方法,每一个值代表着某一采样方法在某一数据集上的AUC值,也就是对某一数据集使用某种采样方法进行重采样来降低不平衡度,然后再使用分类器进行分类,最后计算AUC值;这里,由于本实验采用了多个分类器,每一个分类器对应一个AUC值,为了使表格更加直观,本实验将每个分类器对应得到的AUC值求平均值,表格里看到的便是不同分类器下得到的AUC平均值。表2 主要探讨数据抽样方法在不平衡数据集上的作用。黑体数字对应效果最好的预处理算法。从表2 中可以很容易看出来,对于大多数数据集来讲,BSM+Tomek 的预处理效果要优于BSM;CBOS+ENN 的预处理效果优于CBOS;虽然对BSM 的改进(BSM+Tomek 和BSM+ENN)使得数据集的分类效果得以提升,但是效果不如Gustavo 等人提出的SMOTE+Tomek 和SMOTE+ENN;Gustavo 等人提出的SMOTE+Tomek 和SMOTE+ENN 效果非常好;对于数据极度不平衡的Mc1 数据集,做过抽样提高了分类效果(SMOTE 和CBOS);对于数据不平衡度较小的数据集Kc2和Ar4,做完过抽样后适当做一下清洗(欠抽样)会提高分类效果,BSM+ENN 和BSM+Tomek 都表现出较好的效果,CBOS+ENN 也比CBOS 效果优越;效果最佳的预处理方法是SMOTE 和对SMOTE 的初步改进的算法中,本文对BSM和CBOS的改进算法虽然不及SMOTE和Gustavo提出的改进算法,但是却分别比BSM 和CBOS 优越。
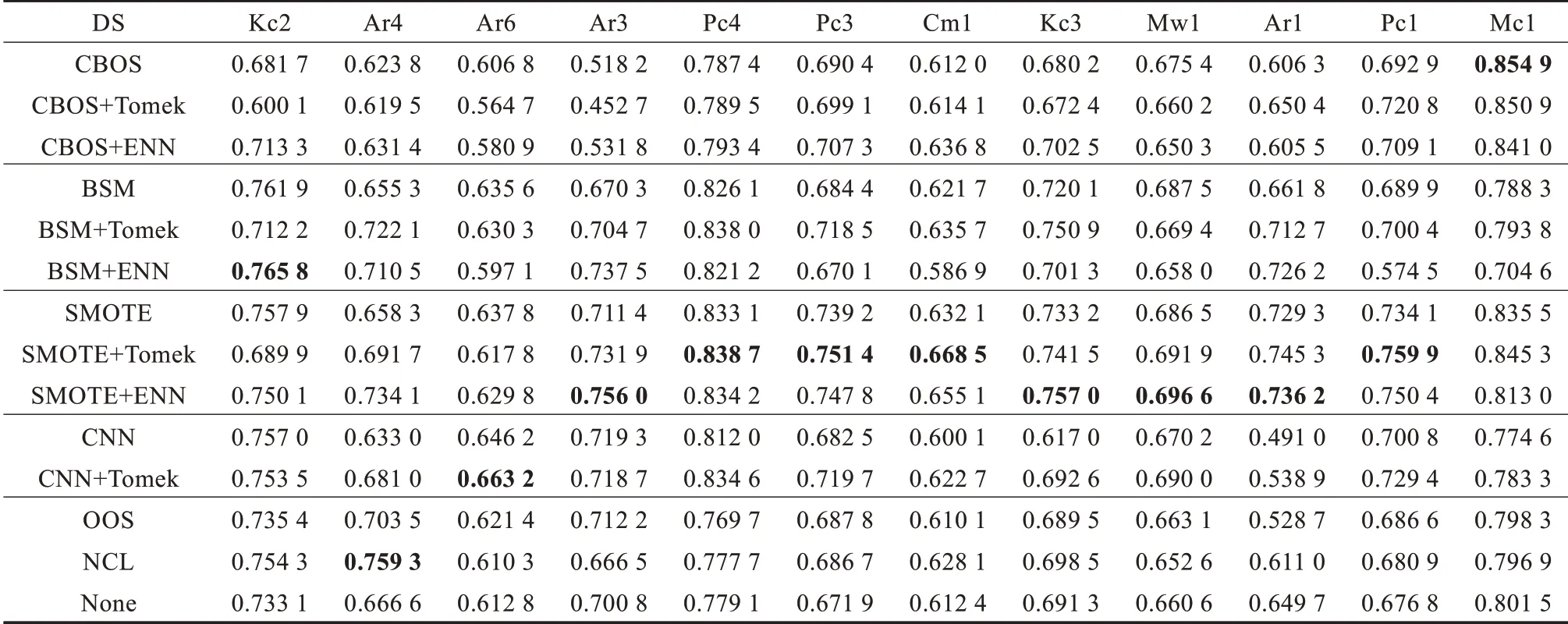
表2 各种采样方法在不同数据集上的AUC 值
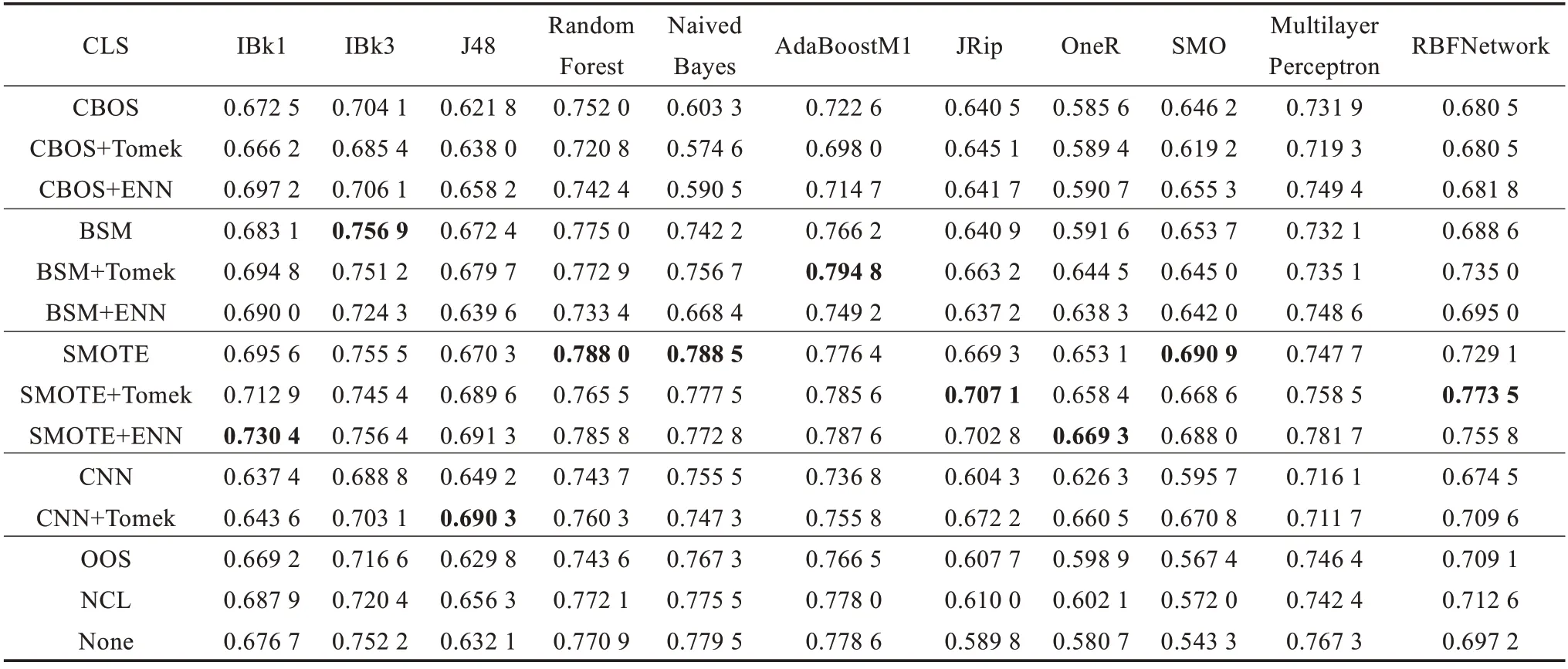
表3 各种分类器在不同数据集上的AUC 值

表4 各采样方法的执行时间 s
表3 的行代表不同的分类器,列代表不同的抽样方法,每一个值代表某一采样方法在不同分类器上的AUC值,探讨不同采样方法与不同的分类器搭配后产生的效果(即AUC值),也就是先通过某种采样方法对不平衡数据集进行重采样来降低不平衡度,然后在不同的分类器上进行分类,最后计算AUC值,实验中对多个不平衡数据集进行了处理,为了使表格更加直观,计算了在多个数据集下得到的AUC值的平均,这些数据集都来自表1 中列出的数据集。从图表中可以看出:对数据集进行BSM 和CBOS 处理后,再进行适当欠抽样会提高分类效果;对于不同的分类器,BSM+Tomek 和CBOS+ENN 的效果也比较稳定,多数情况下效果明显;本文主要探讨数据抽样方法对不平衡数据集分类的影响,不再深入研究分类器的影响。
在本次实验中,使用了多种评价标准,除了上边用到的评价指标之外,还包括precisionfMeasure,kappa 等。这里仅列出AUC指标下的实验结果。
在表4 中,本文给出了各采样方法在同一台机器上的执行时间,作为各采样方法的计算代价,用同一个数据集Mw1进行运行时间的计算,得到了各算法的执行时间,很明显,对于SMOTE、BSM 和CBOS 的改进使得算法的执行时间增加接近一百倍,计算代价增大,同时观察表2,3,AUC值得到了一定程度的提升。
6 结论与展望
本文通过在多个数据集下使用多种数据抽样,并用多个分类器进行训练、分类,用多种评价指标比较分类效果,得到了四种较好的数据抽样方法和有意义的结论,这四种抽样方法在大多数实验所用数据集和分类器下效果比不做数据清洗时的分类效果好,但是本文还有许多值得改进的地方。首先所使用的数据抽样方法都不能做到适用于每一个数据集,没有找到一种稳定的数据抽样方法;其次,本文虽然讨论了抽样方法和分类器对分类效果的影响,但是没有研究数据集对分类效果的影响,希望在下一步的研究中深入研究数据集对分类效果的影响;第三,本文提出的四种改进算法研究了BSM、CBOS、Tomek links 及ENN 的组合,没有研究其他采样方法组合的合理性,而且这四种算法效果虽然优于原来的算法,但是整体效果低于Gustovo的改进算法。
[1] Gewehr J E,Szugat M,Zimmer R.Bio Weka-extending the weak framework for bioinformatics[J].Bioinformatics,2007,23(5):651-653.
[2] Hornik K,Zeileis A,Hothorn T,et al.RWeka:an R Interface to Weka[EB/OL].[2011-11-10].http://www.google.com.hk/#newwindow=1&q=+RWeka:+An+R+Interface+to+Weka%EF%BC%8C2009&safe=strict.
[3] Chapman M,Callis P,Jackson W.Metrics data program[R].NASA IV and V Facility,2004.
[4] Shirabad S,Menzies T J.The PROMISE repository of software engineering databases[EB/OL].[2011-11-10].http://www.google.com.hk/#newwindow=1&q=The+PROMISE+Repository+of+Software+Engineering+Databases&safe=strict.
[5] Tomek I.Two modifications of CNN[J].IEEE Trans on Systems Man and Communications,1976,6:769-772.
[6] Hart P E.The condensed nearest neighbor rule[J].IEEE Trans on Information Theory,1968,14(3).
[7] Chawla N V,Bowyer K W,Hall L O,et al.SMOTE:Synthetic Minority Oversampling Technique[J].Journal of Artificial Intelligence Research,2002,16:321-357.
[8] Han Hui,Wang Wenyuan,Mao Binghuan.Borderline-SMOTE:a new over-sampling method in imbalanced data sets learning[C]//Lecture Notes in Computer Science,2005:878-887.
[9] Gustavo E A,Batista P A,Ronaldo C,et al.A study of the behavior of several methods for balancing machine learning training data[J].SIGKDD Explorations,2004,6(1):20-29.
[10] 宋花玲.ROC 曲线的评价研究及应用[D].上海:第二军医大学,2006.
[11] Wang B X,Japkowicz N.Boosting support vector machines for imbalanced data sets[J].Knowledge and Information Systems,2010,25:1-20.
[12] Li Der-Chiang,Liu Chiao-Wen,Hu S C.A learning method for the class imbalance problem with medical data sets[J].Computers in Biology and Medicine,2010,40(5).
[13] Zhou L G,Lai K K.Benchmarking binary classification models on data sets with different degrees of imbalance[J].Frontiers of Computer Science in China,2009,2(3):205-216.
[14] Anand A,Pugalenthi G,Fogel G B,et al.An approach for classification of highly imbalanced data using weighting and understanding[J].Amino Acids,2010,39:1385-1391.

