平面超声波电动机的研究

王京山，赵学涛

(山东理工大学，山东淄博255049)

0 引 言

超声波电动机具有结构简单、体积小、响应快、不受电磁干扰、断电自锁、直线运动可直接产生等优点，特别适合小型精密运动机构的驱动和控制［1-3］。目前应用的超声波电动机大都只能实现直线或旋转一个自由度的运动。文献［4］研究了一种纵弯复合模态的直线超声波电动机，同样也实现了单一自由度的直线运动。

随着半导体工业、航天、XY精密定位平台和空间机构等许多领域的迅速发展，单一自由度的超声波电动机已无法胜任［5-6］。现在的平面超声波电动机大多采用多定子结构将多个低维运动简单叠加成高维运动，各定子间存在互相耦合、功率互相抵消的现象［7］。针对上述问题，本文设计了一种单定子结构的平面超声波电动机。

1 电机结构及驱动原理

1.1 电机机构

图1为电机结构图，电机采用夹心换能器结构。位于中间的是带有四根螺柱的法兰。指数形变幅杆通过螺纹旋入螺柱，压紧夹在法兰和变幅杆之间的纵振压电陶瓷片(PZTL)和弯振压电陶瓷片(PZTB)。定子采用两对空间位置正交的换能器，由中间法兰连接。四个驱动足位于弯振驻波的波腹处。

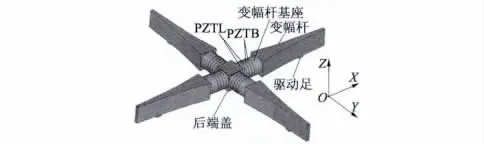
图1 电机结构图

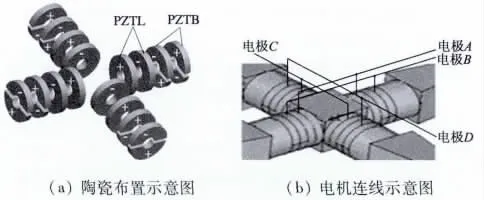
图2 陶瓷分布和电机连线示意图

图2为四组压电陶瓷的布置方式，为增大振动幅值，每组压电陶瓷由两片弯振陶瓷和两片纵振陶瓷构成。每片弯振陶瓷由极化方向相反的两个半圆片陶瓷组成。当弯振陶瓷受到弯振谐振频率的电压激励时，上半片和下半片的膨胀与收缩交替进行，从而激发电机的横向弯曲振动。为获得最佳的激励效果弯振陶瓷的安装位置应当靠近电机弯振波腹处(弯振位移最大处)。纵振陶瓷为圆环结构，相邻两片的极化方向相反。为增加振动稳定性，纵振陶瓷应当安装于电机的纵振节面处(纵振位移最小处)。

1.2 电机驱动原理

电机为十字正交对称结构，在x、y轴方向上的运动原理完全一样，其他方向的直线运动为x、y向运动的合成。因此只分析电机沿x轴方向的运动情况。将C、D电极开路，A、B电极施加22 643 Hz、200 V相位差为π/2的正弦电激励，图3为一个简谐振动周期内电机的工作过程。

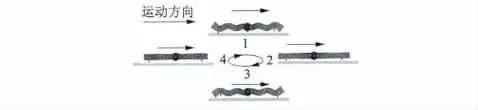
图3 一个周期内电机在x轴方向的振动形态

1和3为驱动阶段，驱动足相对轨道向左运动产生向右的摩擦力，驱动电机向右运动。

2和4为悬浮阶段，由于电机本身的惯性，电机继续向右运动。

4→2阶段，电机处于伸长阶段，且左侧驱动足接触轨道，右侧驱动足抬起，电机左侧驱动足相对于轨道向左运动，电机向右运动。

2→4阶段，电机处于收缩阶段，且右侧驱动足接触轨道，左侧驱动足抬起，电机右侧驱动足相对于轨道向左运动，电机同样向右运动。

将C、D 电极开路，A、B 电极施加22 643 Hz、200 V相位差为-π/2的正弦电激励时，电机向左运动。

1.3 驱动足运动轨迹分析

以驱动足驱动面中心为原点，建立三维直角坐标系。假设驱动足为刚体，取驱动足驱动面中心质点M，质点M的运动轨迹便可代表整个驱动足的运动轨迹。当纵振陶瓷和弯振陶瓷同时进行激励时，质点M振动轨迹的参数方程为:

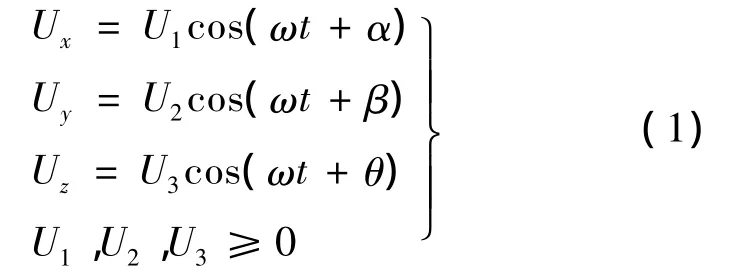
式中:U1、U2、U3分别表示 x轴、y轴、z轴方向的振幅(m);ω表示驱动足固有振动频率(Hz);α、β、θ分别表示x轴、y轴、z轴方向的初相(°)。

联立式(1)中的三个简谐振动方程，消去时间变量t，得到驱动足振动轨迹的一般方程为:

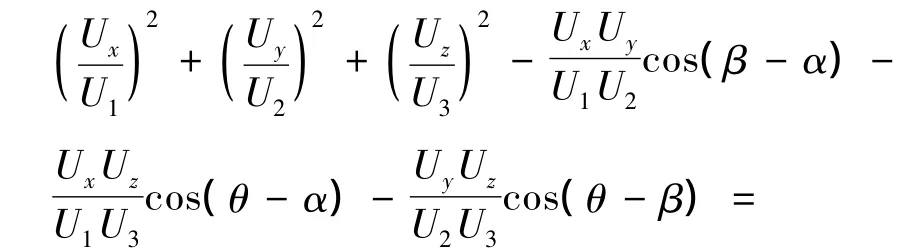
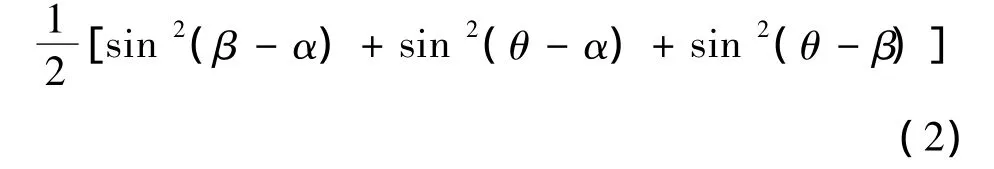
由式(2)可知，驱动质点的振动轨迹方程为以原点为圆心的空间椭圆。

2 平面超声波电动机有限元分析

2.1 有限元模态分析

先根据经典换能器理论，确定一个大致的初始尺寸参数［8］，再对电机结构参数进行模态频率灵敏度分析。选取陶瓷直径d、后端盖长度Lr、变幅杆长度Lh、变幅杆基座厚度Lb和陶瓷厚度t为灵敏度分析参数。当纵向振动模态与弯曲振动模态频率相差较大时，调整其中的敏感参数，实现频率粗调;当纵弯模态频率相差较小时调节其中的非敏感参数，实现频率微调。为得到一个较好的结构尺寸方案需不断地试算，尺寸参数如表1所示。表1电机为电机最终结构尺寸。

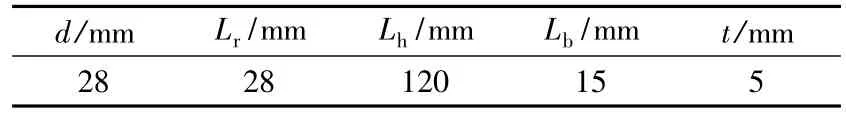
表1 电机结构尺寸

采用表1的结构时，定子纵弯固有频率分别为22 430 Hz和22 467 Hz，两模态频率相差37 Hz，满足频率一致性要求。图4是通过仿真得到的纵振模态振型与弯振模态振型。

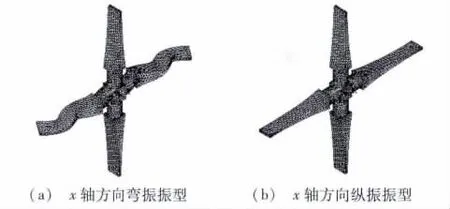
图4 纵弯模态简并后振型图

2.2 有限元谐响应分析

在电极A、B上施加谐振频率电激励，施加电压为100 V、相位差为π/2。为得到驱动质点振幅随频率的变化关系，在包括目标模态频率22 463 Hz在内的频段22 350～22 550 Hz范围内进行有限元谐响应分析。任意选取驱动端面上质点O，利用谐响应分析的Full计算法(完全法)进行求解提取质点O的X向纵振和Z向弯振振幅与频率关系曲线如图5所示。

从图5中可看到，在频率为22 438 Hz处，驱动足x轴、z轴振幅同时达到最大，证明模态分析中纵弯频率简并结果是正确的。驱动足x轴、z轴方向振幅很大，分别为78 μm、60 μm，说明驱动器具备输出较大力矩的性能。

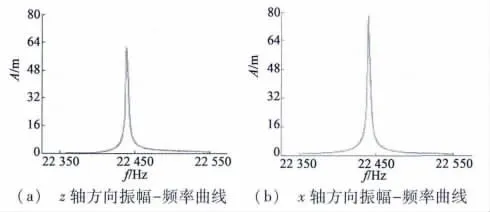
图5 振幅-频率关系

2.3 有限元瞬态分析

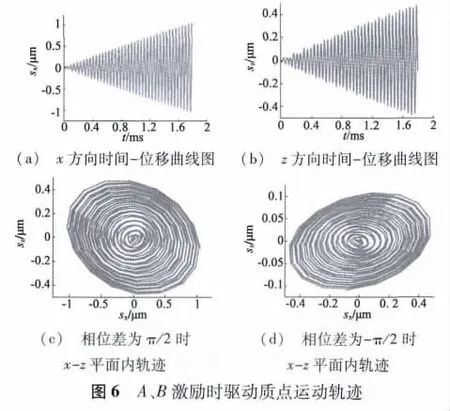
对所建立的有限元模型加载40个周期的正弦电压信号，每个正弦周期设置16个载荷子步，在A、B两路相位差为±π/2时各计算一次，结果如图6所示。从图中可以看到，驱动足的运动轨迹接近于椭圆轨迹，证明本文提出的驱动足的运动方程是正确的。相位差为±π/2时，椭圆轨迹方向相反，产生的驱动力方向也相反，电机可以正反双向运动，证明了本文提出的驱动机理的正确性。

3 结 语

本文提出了一种纵弯复合平面超声波电动机，分析了其工作原理。结合经典变幅杆理论和有限元分析法对电机进行了设计。利用有限元模态分析，实现了平面超声波电动机纵弯两个基本振动模态的简并，进一步借助谐响应分析获取电机两个基本振动模态的输入阻抗特性。用有限元瞬态分析法，提取了驱动足位于换能器弯曲振动的波腹处时的运动轨迹，运动轨迹接近椭圆轨迹。理论分析和有限元仿真结果均表明，纵弯复合型超声波电动机4个驱动足表面质点振动轨迹均为三维的椭圆，并且各驱动足椭圆运动方向一致，电机可以正常工作。

［1］ Roh Y，Kwon J.Development of a new standing wave type ultrasonic linear motor［J］.Sensors and Actuators，2004，112(2-3):196-202.

［2］ Zhao Chunsheng.Research on ultrasonic motors in Nanjing University of aeronautics and astronautics［J］.Journal of Vibration，Measurement and Diagnosis.2005，25(3):167-173.

［3］ 赵淳生.超声电机技术及应用［M］.北京:科学出版社，2007:6-7.

［4］ 石胜君，陈维山，刘军考，等.一种基于纵弯夹心式换能器的直线超声电机［J］.中国电机工程学报，2007，27(18):30-34.

［5］ 郭吉丰，伍建国.航天用大力矩高精度超声波电机研究［J］.宇航学报，2004，25(1):70-76.

［6］ 杨金明，吴捷，张宙，等.平面电动机的现状及发展［J］.微特电机，2003(6):31-34.

［7］ 赵学涛.夹心换能器式多自由度球形超声波电动机研制［J］.微特电机，2009，37(4):7-10.