关于四个收敛性的一个例子

王 龙

(上海师范大学 数理学院，上海200234)

刘宝碇教授在2007 年提出了基于规范性、对偶性、次可加性、乘积测度公理的不确定理论［1］，在不确定理论的公理化体系下又相继提出了不确定规划、不确定风险分析和不确定可靠性分析等，它成为了处理含有不确定变量模型的强有力工具.如今不确定理论在期权定价［2－4］，不确定逻辑辑［5－8］，结构可靠性分析［9－11］，不确定推理［12－13］，不确定风险值及尾部风险值［14］等领域中得到了广泛的应用.并且不确定理论已经在相关领域中取得了很多令人瞩目的成就，得到广大学者的认可和学习.

刘宝碇教授在不确定理论一书中定义了几乎处处收敛、平均收敛、依测度收敛和依分布收敛的概念［15］，并证得平均收敛可以推出依分布收敛和依测度收敛.本文将通过一个算例来研究在不平均收敛的情况下，考察依测度收敛、依分布收敛和几乎处处收敛的敛散性问题，并针对这个问题给出一个不平均收敛的算例，来讨论在这个算例下的敛散性.

1 不确定理论基础知识

定义1.1［15］设Γ 是一个非空集合L是Γ 上的一个σ－代数，L中的每一个元素Λ 称为一个事件.若L上的集函数M满足以下公理

公理1 (规范性)对全集Γ 有M{Γ}=1;

公理2 (对偶性)对任意的事件Λ ∈L，有M{Λ}+ M{Λc}=1;

公理3 (次可加性)对任意的事件列{Λi}，有

公理4 (乘积测度)设Γk是非空集合，Mk分别为其上的不确定测度，k =1，2，…，n.则乘积测度M是乘积σ－代数L1× L2×…× Ln上的不确定测度，且满足

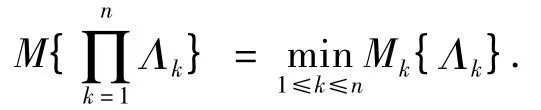
则称集函数M 为不确定测度，并称三元组(Γ，L，M)为不确定空间.

定义1.2［15］不确定变量ξ 是从不确定空间(Γ，L，M)到实数集的一个可测函数，即对于实数上的任意Borel集，{γ|ξ(γ)∈B}∈Γ 是一个事件.

定义1.3［15］设ξ 是不确定变量，如果M{ξ＜0}=0，则称ξ 为非负的.

定义1.4［15］不确定变量ξ 的分布函数Φ 定义为Φ(x)= M{γ|ξ(γ)≤x}.

定义1.5［15］如果对每一个α ∈(0，1)，它的逆函数Φ－1(α)唯一存在，那么不确定分布Φ 称为正则的.

定义1.6［15］如果ξ 是一个不确定变量且正则不确定分布为Φ，那么逆函数Φ－1(α)称为不确定变量ξ 的逆不确定分布.

定义1.7［15］设ξ 是一个不确定变量，则ξ 的期望值被定义为

其中至少有一个积分是有限的.

定义1.8［15］如果不确定变量ξ 有之字形不确定分布

则称不确定变量ξ 为之字形，记作ξ～Z(a，b，c)且a ＜b ＜c.

定义1.9［15］设ξ，ξ1，ξ2…是不确定变量，如果对于每一个ε＞0，都有则称序列{ξi}依测度收敛于ξ.

定义1.10［15］假设不确定变量ξ，ξ1，ξ2…的不确定分布分别为Φ，Φ1，Φ2…，如果对任意的x∈R，，则称序列{ξi}依分布收敛于ξ.

定义1.11［15］假设不确定变量ξ，ξ1，ξ2…且有有限的期望值，如果则称序列{ξi}平均收敛于ξ.

定义1.12［15］假设ξ，ξ1，ξ2…是定义在不确定空间(Γ，L，M)，如果存在事件Λ 且M{Λ}=1，使得则称序列{ξi}几乎处处收敛于ξ.

定理1.1［15］设ξ 是一个不确定变量且正则不确定分布为Φ，如果期望值存在，那么E［ξ］=

定理1.2［15］如果不确定变量ξ 是之字形的，那么ξ 的逆分布为

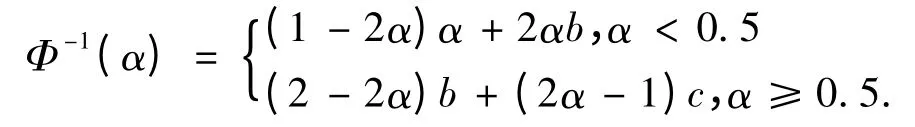
2 算例

例 设ξi，ξ 是定义在不确定空间(Γ，L，M)上的不确定变量，且ξ ～Z(a，b，c)，ξi～Z(ai，bi，ci)，i=1，2，…，当i→∞时，ai→a，bi→b，ci→c，其中c＞b＞a.试讨论不确定变量ξi，ξ 的如下关系:

(1)ξi是否依分布收敛于ξ?

(2)ξi是否平均收敛于ξ?

(3)ξi是否依测度收敛于ξ?

(4)ξi是否几乎处处收敛于ξ?

证 因为ξ ～Z(a，b，c)，所以ξ 的不确定分布为

设Ψ1，Ψ2分别是不确定变量(ξi －ξ)和(ξ－ξi)的不确定分布，相应的逆不确定分布分别为Ψ1－1(α)和Ψ2－1(α).由不确定理论的运算法则可知且

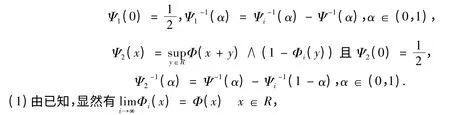
从而ξi依分布收敛于ξ.

(2)由期望值定义，得

从而当i→+∞时，E［|ξi－ξ|≥ε］→0，所以ξi依测度收敛于ξ.

(4)在不确定空间(Γ，L，M)中，由ξ 和ξi的不确定分布，易得其密度函数分别为

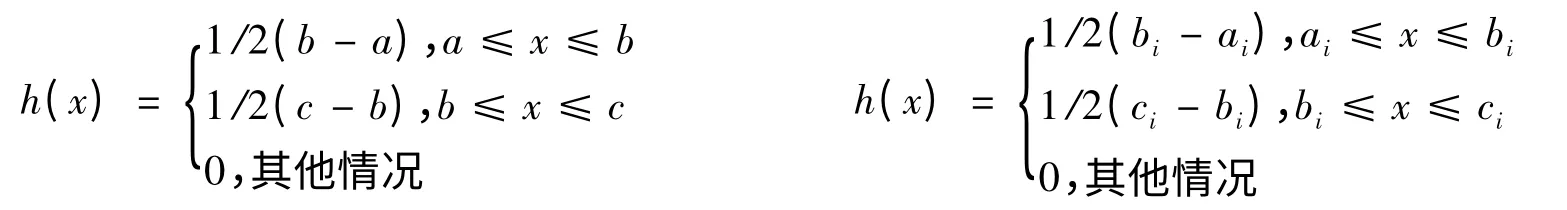
取Γ=［a，c］，令ξ(γ)=γ，当x∈［a，b］时，则M{ξ(γ)≤x}=(x － a)/2(b － a).当x∈［b，c］时，则M{ξ(γ)≤x}=(x + c －2b)/2(c － b).

同理取Γ=［ai，bi］，令ξi(γ)=γ.

当x∈［ai，bi］时，则M{ξi(γ)≤x}=(x － ai)/2(bi － ai).当x∈［bi，ci］时，则M{ξi(γ)≤x}=(x+ ci －2bi)/2(ci － bi).

又因为i→+∞时，［ai，bi］→［a，b］，［bi，ci］→［b，c］且［ai，ci］→［a，c］，

本文列举了一个算例，并通过本算例给出了证明不确定理论中四个收敛的具体过程，也即证明了对于之字形的不确定变量不是平均收敛的，而是依分布收敛、依测度收敛和几乎处处收敛的.同样，对于线性的或正态的不确定变量仍然可用同样的方法推理证明.参考文献:

［1］Liu B. Uncertainty Theory［ M］. 2nd ed. Berlin:Springer－Verlag，2007.

［2］ Chen X. American Option Pricing Formula for Uncertain Financial Market［J］. International Journal of Operations Research，2011，8(2):32 －37.

［3］ Peng J，Yao K. A New Option Pricing Model for Stocks in Uncertainty Markets［J］. International Journal of Operations Research，2011，8(2):18 －26.

［4］ Xu J，Peng J. Barrier Options Pricing in Uncertain Financial Market［C］// Proceedings of the Eighth International Conference on Information and Management Sciences. Kunming，China，July 20 －28，2009:821 －826.

［5］ Gao Y.Analysis of k－out－of－n System with Uncertain Lifetimes［C］//Proceedings of the Eighth International Conference on Information and Management Sciences，Kunming，China，July 20 －28，2009:794 －797.

［6］ Wang Z.Structural Reliability Analysis Using Uncertainty Theory［C］//Proceedings of the First International Conference on Uncertainty Theory，Urumchi，China，August 11 －19，2010:166 －170.

［7］ Wang Z. The Application of Uncertainty Theory in Structural Reliability［D］. Tsinghua University，2010.

［8］ Chen X，Ralescu A. A Note on Truth Value in Uncertain Logic［C］//Proceedings of the Eighth International Conference on Information and Management Sciences，Kunming，China，July 20 －28，2009:739 －741.

［9］ Liu B. Uncertain Entailment and Modus Ponens in The Framework of Uncertain Logic［J］. Journal of Uncertain Systems，2009，3(4):243 －251.

［10］ Liu B. Uncertain Logic for Modeling Human Language［J］. Journal of Uncertain Systems，2011，5(1):3 －20.

［11］ Liu B. Why is There a Need for Uncertainty Theory?［J］. Journal of Uncertain Systems，2012，6(1):3 －10.

［12］ Gao X，Gao Y ，Ralescu D.On Liu’s Inference Rule for Uncertain Systems，International Journal of Uncertainty［J］.Fuzziness and Knowledge－Based Systems，2010，18(1):1 －11.

［13］ Liu B.Uncertain Set Theory and Uncertain Inference Rule with Application to Uncertain Control［J］.Journal of Uncertain Systems，2010，4(2):83 －98.

［14］ Peng J. Value at Risk and Tail Value at Risk in Uncertain Environment［C］//Proceedings of the Eighth International Conference on Information and Management Sciences. Kuming，China，July 20 －28，2009:787 －793.

［15］ Liu B. Uncertain Theory［M］. 4th ed. Berlin:Springer－Verlag ，2010.