Ohta-Hirota 方程的延拓结构及Lax 对

沈柳平

(柳州师范高等专科学校 数学与计算机科学系，广西 柳州545004)

1 延拓结构理论

为简便起见，讨论KdV 方程［1］

的延拓结构.先引入新的独立变量ux=p，uxx=px=q，这样(1)式可写成如下一阶偏微分方程组

在流形M={x，t，u，p，q}上定义一组外微分2 －形式

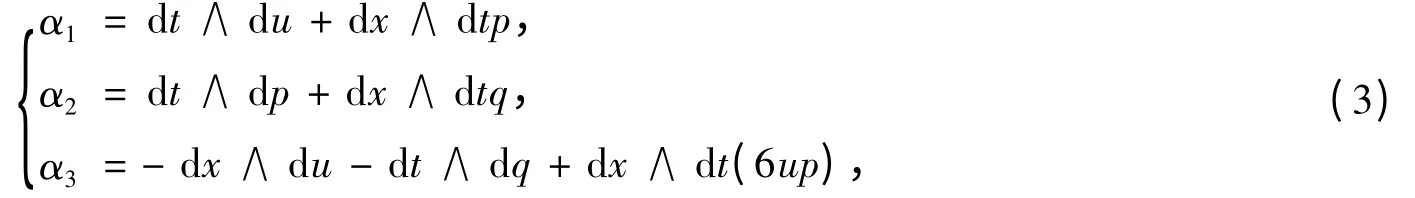
其中d 表示外导数，∧表示外积.(3)式前2 项对应于引入新变元的项，后一项对应于原始方程的项.对(3)式作外微分，可得

因此I={α1，α2，α3}在流形M上构成闭理想，当αi(i=1，2，3)限制到解流形U={u(x，t)，p(x，t)，q(x，t)}上为零时，则可以回到方程(1).

2 Ohta－Hirota 方程的延拓结构及Lax 对

有下面的结论.

定理 如果闭理想I={αi，ωi}限制到流形S上为零，则Ohta－Hirota 方程存在Lax 对.

证明:首先引入新独立变量vx=r，vxx=s，Ux=p，Uxx=q，则在流形S={x，t，v，U，r，s，p，q}上定义微分2 －形式

易证I={αi，i=1，2，…，6}是闭理想［4］.根据延拓结构理论，将I限制到解流形S={x，t，v(x，t)，U(x，t)，r(x，t)，s(x，t)，p(x，t)，q(x，t)}上为零时，则可回到方程(5). 下面来找Ohta －Hirota 方程的Lax 对.

引进n个微分1 －形式

将以上生成元代入到(10)、(11)、(13)、(15)式中，可得F和G的具体表达式

由相容性关系yxt=ytx，便可得方程(5).

［1］ Huang N N. Darboux transformation of KdV equation［J］. Phys，1992，A25:469 －475.

［2］ Humphreys J E.Introduction to Lie algebras and representation theory［M］. Berlin:GTM Springer，1972.

［3］ YOhta O R，Hirota R. Quasideterminant solutions of a non－Abelian Hirota－Miwa equation［J］. Phys Soc Jpn，2007，76:24 －35.

［4］ Geng X G ，Wu Y T. From the special 2 +1 Toda lattice to the Kadomtsev－Petviashvili equation［J］. Math Phys，1997，38:3069 －3077.