浅谈基于拟力法的Benchmark模型消能减震结构非线性设计

韩晓雨，曲激婷，姜峰

浅谈基于拟力法的Benchmark模型消能减震结构非线性设计

韩晓雨，曲激婷，姜峰

本文介绍了当前国际结构振动控制的公共平台Benchmark模型，并对拟力法的基本原理进行了简要介绍，基于拟力法来进行消能减震结构非线性设计方便可行，具有一定的优越性。

Benchmark模型；拟力法；非线性；消能减振结构

韩晓雨/大连理工大学建设工程学部助教，硕士（辽宁大连116023）；曲激婷/大连理工大学建设工程学部讲师，博士（辽宁大连116023）；姜峰/大连理工大学建设工程学部教授，硕士（辽宁大连116023）。

一、引言

结构抗震防灾是一项巨大的研究领域，包含众多研究内容，如何降低地震灾害对于结构造成的破坏、控制震害损失范围对于工程师们来说是非常关键的问题。基于性能的抗震设计以结构抗震性能分析为基本出发点，根据结构的用途和使用者的要求，采用合理的抗震性能目标和合适的结构抗震措施进行设计，使结构在各种水准的地震作用下，破坏损失能够为业主选择和承受，在安全可靠和经济合理之间达到平衡[1]。

消能减震技术是一种迅速发展起来的新技术，近年来受到各国学者的广泛重视。通过在结构的某个部位增设消能器，以增加结构阻尼，达到减小结构在风和地震作用下反应的目的，减轻灾害。Benchmark问题是指在统一的结构模型、性能指标和相同的环境条件下，建立一整套完善的系统检验和评价体系，进而为不同的结构振动控制方案和策略的比较提供一个良好的公共平台[2]。

以拟力法为基础的动力弹塑性时程分析方法，与传统的以有限元为基础的时程分析方法相比，运算速度快，动力稳定性好，材料适用面广[3]。由于拟力法作为一种结构动力分析的近似方法具有很多独特的优越性，近年来，随着基于拟力法的非线性计算理论的不断发展壮大，国内外研究人员逐渐将拟力法应用于结构的地震能量反应分析、结构的线性预测优化控制、随机动力分析及消能减震结构的地震反应分析等各个领域中，结合拟力法和基于性能的设计方法，设计合理的性能指标，进行消能减震结构非线性设计已成为一个重要的课题。

二、Benchmark模型

结构振动控制作为一种新技术，近年来已在世界多处工程中得到了应用。众所周知，结构的振动控制效果与结构和控制系统的多种因素有关，其中包括环境作用、结构特性、控制装置、控制算法、观测变量等等。研究人员对各种控制方法进行了研究，然而他们给出的试验或仿真结果却没有一个统一的尺度来进行衡量，他们所给出的算法和减振装置性能的优劣自然也就无从比较。为此，我们一直希望能够建立一种统一的模型和控制性能指标，以检验和评价不同控制系统在不同环境因素影响下的适用性和有效性[4]。Benchmark问题的理念最早提出是在1994年，而后从1997年起，美国土木工程师协会 (ASCE)结构控制委员会分阶段逐渐提出了Benchmark模型。

Benchmark模型问题是指在相同的结构模型、环境干扰以及性能指标下，建立一套完整的用于检验和评价结构振动控制系统的体系，提供良好的公共平台，用于研究和比较隔震方案、控制算法、控制装置和控制效果[5]。

随着研究的不断深入，近年来Benchmark问题的研究中关于地震控制的内容已经不再仅仅局限于结构控制试验系统，也不再局限于控制理论和控制算法的分析比较。为了实现结构振动控制从理论过度到实践这一目标，Benchmark问题的研究正在朝着实际工程应用化和实际工程对象侧重化这一方向逐步迈进。

三、拟力法的基本理论

（一）拟力法研究现状

固体力学早期主要采用变刚度有限元法，拟力法是在1968年由Lin等人[5]最早提出，用于连续体力学的非线性计算。到了1999年，Wong等人[6]基于拟力法建立了框架结构能量反应分析模型，将拟力法应用在框架结构的动力弹塑性时程分析中，给出了详细的震中结构能量分析计算过程和求解方法。此后，拟力法被Wong等人[7-9]应用在结构的线性预测优化控制和随机动力分析等领域中，很好地解决了主动控制的时滞问题，在较高的效率下，得出的结果也相对正确、可靠。2007年，Chao等人[10]提出了基于拟力法的改进计算模型，采用3个不同的塑性机制对钢筋混凝土梁柱单元进行模拟，实现了框架柱在往复荷载作用下的刚度退化问题。

在中国，2009年，李钢等人[11]将拟力法应用在消能减震结构的地震反应分析中，验证了消能减震结构的计算模型及计算方法是正确的、有效的。2010年，李钢等人[12]在线性MBC控制策略的基础上，结合拟力法提出了解决结构非线性问题的MBC控制策略，实现了MBC策略在非线性结构震动控制领域的应用，解决了以往基于有限元求解结构动力分析时的时间长、速度慢、占用存储空间大等问题。

（二）拟力法的基本思想

拟力法的基本思想是假定结构在进入非线性时，构件的其他部分始终保持线性，只有在构件端部集中存在有塑性变形，这些塑性集中区域即为塑性铰（PHLs），而结构的塑性位移也是由这些塑性铰产生的转动所引起。通过将塑性铰等效为理想铰，并建立塑性铰与结构水平位移及水平恢复力之间的关系，即可实现结构的非线性求解过程[11]。

考虑一个单自由度体系的力和位移关系曲线：

图1 单自由度体系力和位移的关系曲线

如图1所示：Fy和xy分别表示屈服力和屈服位移，而F（t）和x（t）分别表示瞬时的力和位移。将初始刚度曲线OA延伸直至其达到点B处的力F（t），将对应于点B的位移定义为弹性位移x′（t），总位移x（t）与弹性位移x′（t）之差为非弹性位移x″（t）。弹性位移x′（t）代表了卸载后可以恢复的位移，而非弹性位移(塑性位移)x″（t）则代表了卸载后不可恢复的永久变形。将此概念表示为数学形式[6]即为：

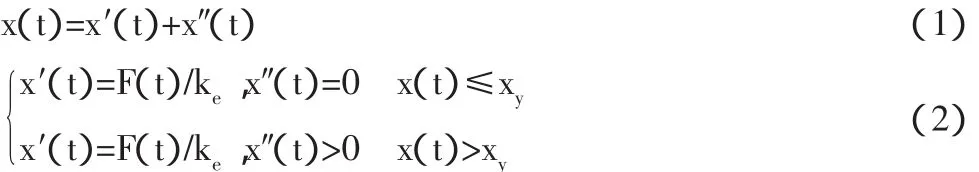
其中，ke表示初始刚度，

因此，对应于任一位移时弹簧中的力恒等于弹性位移与初始刚度之积，即

方程（4）表明了改变系统的位移对于力的影响。弹性位移不是常量，其将随力的变化而变化；因此，弹性位移并不等于屈服位移，即x′（t）≠xy。

从以上的讨论中可以发现拟力法在求解结构非弹性响应时，通过位移的变化而非刚度的变化来给出同等水平的力，这是拟力法的主要思想。

（三）拟力法的公式推导[6-13]

多层结构的位移向量可写为：

X（t）代表总位移；X′（t）代表弹性位移；X″（t）代表非弹性位移（即塑性位移）。矢量中的每一项代表结构一个位移自由度方向上的位移。

结构的非弹性位移通常是由结构构件在某些部位的非弹性变形引起的。这些非弹性变形包括在支撑框架中撑杆的非弹性拉伸，受弯框架中梁的塑性转动，或基础隔震体系中基础隔震器的屈服。

在一个抗弯框架体系中，必须计算出每一结构构件中的力以确定结构响应是在弹性还是在非弹性区域。其中构件两端的弯矩非常关键，因为在较大的侧向动力荷载作用下其经常会超过构件的承载能力。在这些超过屈服弯矩的部位，构件将会发生屈服，这些部位即为塑性铰。结构的塑性转动自由度即由这些塑性铰来确定。

对于一个多自由度体系，可能形成塑性铰处的总弯矩向量可由以下方程描述：

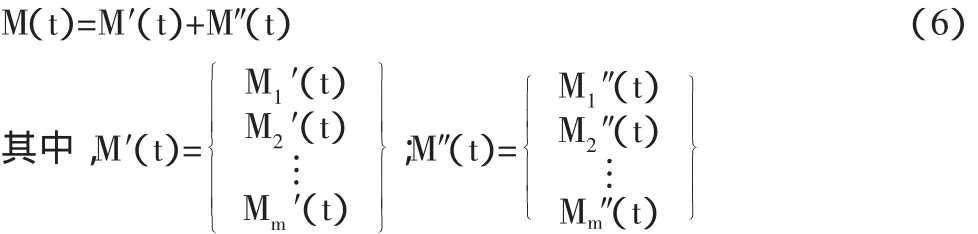
其中M′（t）为由弹性位移引起的弹性弯矩；M″（t）为由非弹性位移引起的剩余弯矩。m值代表潜在塑性铰的总数目。

考虑剩余弯矩矢量M″（t）。当塑性转动出现在结构的某些塑性铰上时，其塑性转动可由一系列虚拟力来代替。

每一个位移自由度处的外加力F（t）通过结构的总体刚度与弹性位移矢量相关，如果给出的是总位移而不是弹性位移，则首先由方程（5）求解X′（t）并将结果代入。之后使用方程（11），可得位移自由度方向的作用力为：

方程（19）中，n为位移自由度数，m为塑性铰自由度数，结构总体刚度矩阵则是一个（n+m）×（n+m）矩阵。当给出外力 F（t），则X（t），M（t）和θ″（t）是方程（19）中的未知量。同样，当给出总位移X（t），则F（t），M（t）和θ″（t）即为方程（19）中的未知量。在其中任一种情况下都会有（n+2m）个未知量。矩阵方程（19）中有（n+m）个方程，每个塑性铰处存在转角和弯矩间关系式为m个，因此总共有（n+2m）个方程。因此，方程（19）中的未知量可解。

四、基于拟力法的消能减震结构非线性设计的优越性

非线性分析、设计是结构动力学一个意义重大的研究领域，尤其是对于使用寿命中可能经受如地震或强风等超荷作用的结构。基于拟力法，通过改变位移而非刚度来进行结构的非线性动力分析及设计，这样做有以下几个主要的优势。

1.该方法可以用于分析具有不同属性的结构，不仅可以用于具有应变硬化属性的结构，也可用于具有应变软化属性的结构[6]。

2.在考虑结构动力特性时，该方法使状态空间数值积分方法能够适用于非线性分析，因此可以获得较高的准确度。

3.通过将每个非线性变形都视为一个自由度，该算法使得结构的所有非线性行为都可以被写为一个方程。

4.与传统的变刚度有限元动力分析方法相比，基于拟力法求解在很大程度上减小了计算量，降低了求解速度，并且能够实时再现结构构件非线性状态[12]，因为状态空间方法中状态转移矩阵基于初始刚度得出且始终保持不变，因此只需要一次计算。

5.拟力法采用塑性铰来模拟结构的塑性性态，因此，在对框架结构进行能量反应分析时，能够了解荷载作用过程中任意时刻结构的破坏情况，及时关注塑性铰的出现时间、出现位置、转动量，以及转角变形情况及层间位移等数据，尤其对于分析结构因增加消能支撑而引发了的塑性铰变化这一特点，是其他方法无法比拟的[11]。

6.由于拟力法是将结构的塑性变形区域考虑为塑性铰，因而整个结构的滞回耗能即为各塑性铰的滞回耗能之和，如将拟力法与能量分析结合，即可获得任意时刻滞回耗能在各杆件的分布状况，有效地解决耗能分析难以进入构件层面的问题[14]。

[1]孙俊，刘铮，刘永芳.工程结构基于性能的抗震设计方法研究[J].工程结构基于性能的抗震设计方法研，2005，31（3）：98-101

[2]田石柱，王立伟，王大鹏.基于 ANSYS软件 benchmark模型耗能减振控制分析[J].地震工程与工程振动，2006，26（6):184-189

[3]刘哲锋，沈蒲生.基于拟力法的地震能量反应分析［A］.防震减灾工程研究与进展——全国首届防震减灾工程学术研讨会论文集[C].2004：184-190

[4]欧进萍.结构振动控制：主动、半主动和智能控制[M].北京:科学出版社，2003：490-510

[5]Lin TH.Theory of inelastic structures[M].New York:Wiley，1968

[6]Wong Kevin K F，Yang Rong.Inelastic dynamic response of structures using force analogymethod[J].Journal of Engineering Mechanics，1999，125（10):1190-1200

[7]Wong Kevin K F，Yang Rong.Predictive instantaneous optimal control of inelastic structures during earthquakes[J].Earthquake Engineering and Structural Dynamics，2003，32:2179-2195

[8]Wong Kevin K F.Predictive optimal linear control of inelastic structures during earthquake[J].Journal of Engineering Mechanics，2005，131（2):131-152

[9]Wang Zhe，Wong Kevin K F.Stochastic dynamic analysis of inelastic structures using force analogymethod[J].Journal of Engineering Mechanics，2007，（4):414-421[10]Chao SH，Loh C H.Inelastic response analysis of reinforced concrete structures using modified force analogy method[J].Earthquake Engineering and Structural Dynamics，2007，36（12):1659-1683

[11]李钢，李宏男，李瀛.基于拟力法的消能减震结构地震反应分析[J].土木工程学报，2009，42：（4）：55-63

[12]李钢，刘凤，李宏男.基于拟力法的MBC非线性控制[J].震动工程学报，2010，23（3）：324-332

[13]Wong Kevin K F，Yang Rong.Earthquake response and energy evaluation of inelastic structures[J].Journal of Engineering Mechanics，2002，128（3):308-318

[14]刘哲锋，沈蒲生，龚胡广.基于拟力法的框架结构静力弹塑性分析[J].建筑科学与工程学报，2006，23（3）：32-36

TU352

A

1671-6531（2013）07-0006-03

姚 旺