基于佳点集构造的改进量子粒子群优化算法

陈义雄，梁昔明，黄亚飞

(1. 中南大学 信息科学与工程学院，湖南 长沙，410083；2. 湘潭钢铁公司 培训中心，湖南 湘潭，411104；3. 北京建筑工程学院 理学院，北京，100044)

基于佳点集构造的改进量子粒子群优化算法

陈义雄1,2，梁昔明1,3，黄亚飞1

(1. 中南大学 信息科学与工程学院，湖南 长沙，410083；2. 湘潭钢铁公司 培训中心，湖南 湘潭，411104；3. 北京建筑工程学院 理学院，北京，100044)

针对粒子群优化算法易出现早熟收敛及局部搜索能力不足的特点，提出一种改进的量子粒子群优化算法(IQPSO)。该算法在量子粒子群优化算法(QPSO)的基础上，引入佳点集初始化量子的初始角位置，提高初始种群的遍历性；在粒子角速度位置更新中，采用混沌时间序列数，促使粒子跳出局部极值点；为避免粒子陷入早熟收敛，在算法中加入变异处理。仿真实验结果表明：与标准粒子群优化(SPSO)算法和量子粒子群优化(QPSO)算法比较，提出的算法具有快速的收敛能力、良好的稳定性，其优化性能有较明显的提高。

粒子群优化；混沌；早熟收敛；佳点集；量子粒子群优化

粒子群优化(PSO)算法[1]最初是由 Kenedy和Eberhart于1995年受人工生命研究结果的启发，在模拟鸟类捕食行为时提出的一种全局优化算法。PSO不要求被优化函数具有可微、可导、有无梯度等性质，并且算法具有概念简单、参数设置少、易于实现、收敛速度快等特点，自提出以来得到广泛的应用。由于PSO容易陷入局部最优、算法收敛精度不高、收敛速度慢、容易遭受维数灾的困扰[2]等缺点，很多学者对此提出相应的改进策略。李辉[3]将禁忌搜索算法与粒子群算法结合，提出禁忌粒子群算法；王波等[4]在粒子群优化算法中引入进化算法，提高了预测电网短期负荷的预测精度；林楠[5]提出了动态粒子群优化算法，改善了算法的全局寻优能力和收敛速度；吴军和李为吉[6]将免疫算法中浓度的概念引入粒子群算法中，提出了一种基于浓度概念的竞争排挤粒子群算法；梁昔明等[7]将动态随机搜索和佳点集引入到粒子群优化算法中，提高了收敛速度和粒子跳出局部最优能力；丁华福等[8]针对惯性权重线性递减粒子群算法不能适应复杂的非线性优化搜索过程的问题，提出了一种基于Sigmoid函数和聚集距离变化率改变惯性权重的方法；王俊伟和王定伟[9]利用梯度信息来影响粒子速度的更新，提高了算法的搜索效率；李士勇和李盼池[10]将量子进化算法(QEA)融合到PSO中，提出一种新颖的量子粒子群优化算法(QPSO)。这些改进算法在很大程度上依赖于对初始参数的选择，容易陷入局部最优，导致早熟收敛；部分算法虽然提高了局部搜索能力，避免了早熟收敛，但不同程度地降低了收敛速度[11]。针对上述问题，本文作者提出一种基于佳点集构造的改进量子粒子群优化(IQPSO) 算法。运用佳点集构造初始化量子位置的初始角度，提高量子初始位置的遍历性；在算法中引入变异算子增加了种群的多样性，避免早熟收敛。

1 标准粒子群优化算法

粒子群优化算法模拟鸟群飞行觅食的行为，通过鸟之间的集体协作与竞争使群体达到目的。为改善算法的收敛性能，Shi和 Eberhart[12]引入惯性权重的概念，对速度的更新方程做了修改，这种方法被称为标准粒子群优化(SPSO)算法。标准粒子群优化 (SPSO)算法可描述为：第i个粒子在D维搜索空间中的位置为 xi=[xi,1，xi,2，…，xi,D]T，速度为 vi=[vi,1，vi,2，…，vi,D]T，M为粒子的种群规模，第i个粒子搜索到的历史最优位置为Pi=[pi,1，pi,2，…，pi,D]T，整个种群搜索到的最优位置为Pg=[pg,1，pg,2，…，pg,D]T，将xi带入目标函数计算其适应值，同时利用下列公式不断地更新粒子的位置和速度，并比较适应值直至找到最优解。

其中：i=1，2，…，M；j=1，2，…，D；t为迭代次数；w为惯性权重；c1和c2为学习因子；r1和r2为区间[0,1]内的随机数。另外，粒子在每一维飞行的最大速度为Vmax，即式(1)中|vi,j|＞Vmax时，取|vi,j|=Vmax。粒子在解空间内不断的进行个体寻优与全局寻优，直到达到规定的迭代次数或满足给定的误差标准为止。

2 改进的量子粒子群优化算法

2.1 改进的量子粒子群优化算法的基本思想

为提高标准PSO算法的局部搜索能力，避免陷入早熟收敛。本文作者在QPSO算法的基础上，结合佳点集构造理论，提出一种改进的量子粒子群优化算法。其基本思想是在量子粒子群算法中，采用佳点集构造理论取点分布均匀的特点，使种群初始化更为均匀，提高初始种群的遍历性；将惯性因子设置为混沌时间序列数，使粒子能跳出局部极值点；从而达到全局寻优的目的。

2.2 量子粒子群优化算法

量子粒子群[10](QPSO)算法是受量子力学的启发，最近几年发展起来的一种优化方法。在QPSO算法中，为提高解空间的遍历能力，该算法采用概率幅的编码机制；采用量子旋转门实现粒子的移动，用量子非门对粒子进行变异；量子位幅角增量用下式进行更新。

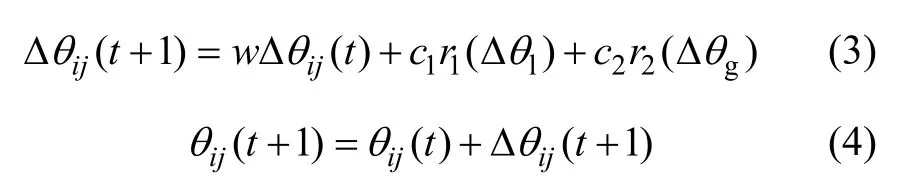
其中：c1，c2，r1和r2的含义与其在SPSO算法中的含义相同，取值也基本相似；w为混沌时间序列数映射到[0.1，0.9]区间上的数值；θ为量子比特的相位；Δθl为当前个体和个体之间的角度差；Δθg为当前个体与全局最优之间的角度差，计算公式如下：

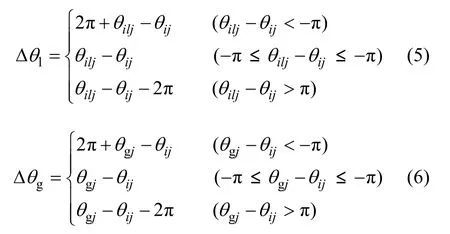
在QPSO中，用量子非门实现变异操作。其操作过程如下：

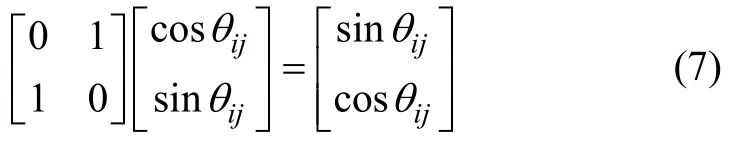
令变异概率为pm，每个粒子在(0,1)之间设定一个随机数，则用量子非门兑换2个概率幅，该粒子记忆的自身最优位置和转向角仍保持不变。

在QPSO中由于采用量子位概率幅的编码机制扩展解空间的遍历性，在群体规模不变的情况下，有利于提高算法的优化效率。

2.3 佳点集

佳点集最初由华罗庚等[13]提出，其基本定义与构造为：设Gs是s维欧氏空间中的单位立方体，如果r中：C(r，ε)是只与r和ε(ε是任意的正数)有关的常数，则称Pn(k)为佳点集，r为佳点。取r={2cos(2πk/p)，1≤k≤s}(p是满足(p−3)/2≥s的最小素数，则r为佳点。

采用佳点集法和随机法生成二维初始种群进行对比，如图1所示。从图1可见：在相同的取点个数下，佳点集法取点比随机法取点更为均匀。因此，将Gs上佳点映射到目标求解空间，使初始种群更具有遍历性，从而更好的达到全局寻优的目的。利用佳点集法产生的二维图形，无论经过多少次计算，只要种群数量一定，其产生的图形都是确定不变的，即具有相当的稳定性。

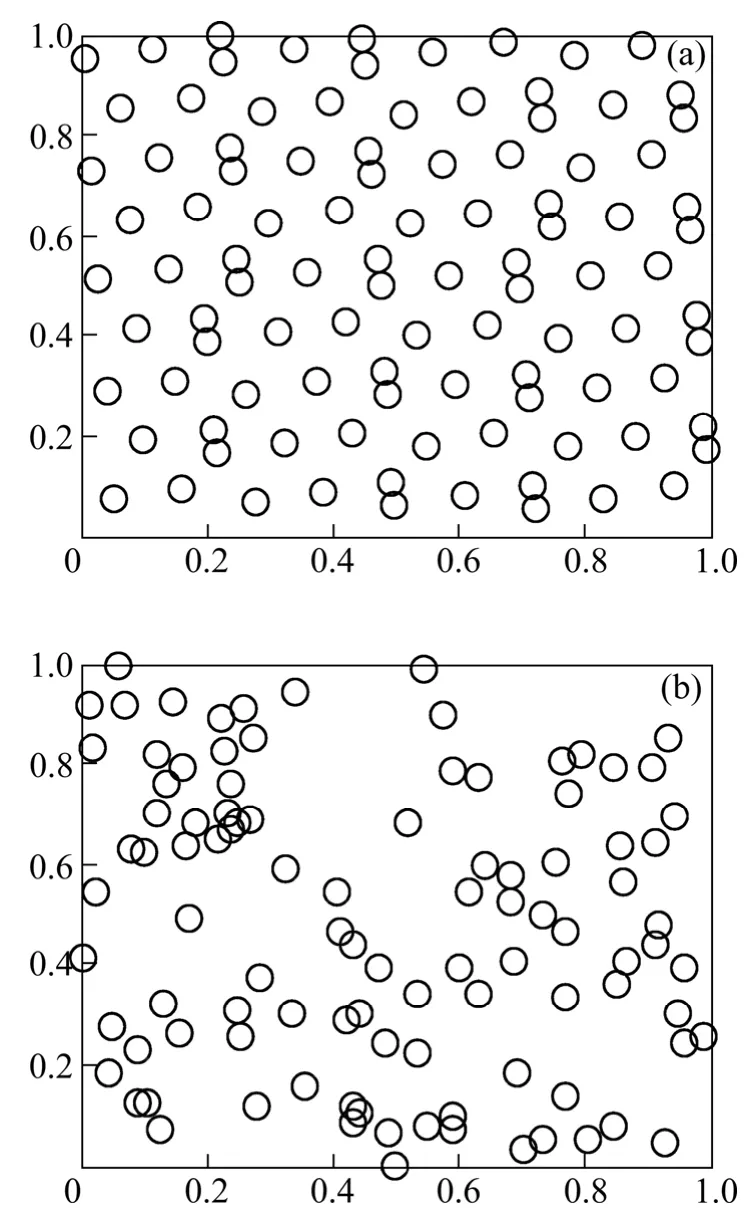
图1 二维初始种群分布图Fig. 1 2-D initial population distribution

2.4 改进量子粒子群优化算法步骤

算法的具体步骤如下：

Step 1：设置IQPSO初始化的有关参数，如种群规模、变量个数、迭代次数、解空间范围等。

Step 2：应用佳点集理论对种群幅角进行初始化。

Step 3：利用适应度函数对每个粒子的初始位置进行评价，计算出每个粒子位置的适应值。若粒子目前的位置优于自身记忆的最优位置，则用目前位置替换；若目前全局最优位置优于到目前为止搜索到的最优位置，则用全局最优位置替换。

Step 4：根据式(3)和(4)更新粒子的位置。

Step 5：对每个粒子依变异概率，根据式(7)实现变异操作。

Step 6：返回Step 3循环计算，直到满足收敛条件或迭代次数达到最大限制为止。收敛条件由具体问题决定。

3 数值仿真

为测试本文提出的IQPSO算法的优化效果，进行大量的计算机数值实验，并且与SPSO和QPSO[10]进行实验比较。选取其中的某些测试函数[14](如表 1所示)，分别采用SPSO，QPSO和IQPSO算法各优化20次，3种算法种群规模均取20，最大迭代次数取300。算法的参数设置：惯性权重w取值范围为[0.1，0.9]的混沌时间序列数，自身因子和全局因子取c1=c2=2.0，变异概率取pm=0.05，收敛精度设为 1×10−2。优化结果对比如表2所示，其中BEST，MEAN和SD分别表示算法独立运算300次的最好适应值、平均适应值和适应值方差；表2中的收敛步数表示达到收敛精度计算的平均步数(没有达到收敛精度的不进行计算)。

由表 2的数据对比可知：对 6个函数的测试，IQPSO算法产生适应值的最好结果、平均结果都优于SPSO和QPSO算法产生的结果，更接近于目标函数值；6个函数的标准差比较，IQPSO算法产生的标准差更小，说明IQPSO算法在函数的每次优化过程中稳定性更高；从收敛次数看，在优化过程中IQPSO达到精度要求的次数明显高于SPSO和QPSO算法。

为更直观地反映算法的寻优效果，将IQPSO算法与SPSO算法、QPSO算法的相关测试函数的收敛曲线的结果进行对比，如图2所示。从图2可以看出：对6个函数的测试，在迭代后期，IQPSO算法比SPSO、QPSO算法更易跳出局部极值点，避免早熟收敛。从图2(f)可以看出：SPSO算法在迭代后期已陷入局部极值点。

表1 基准测试函数Table 1 Benchmark test function

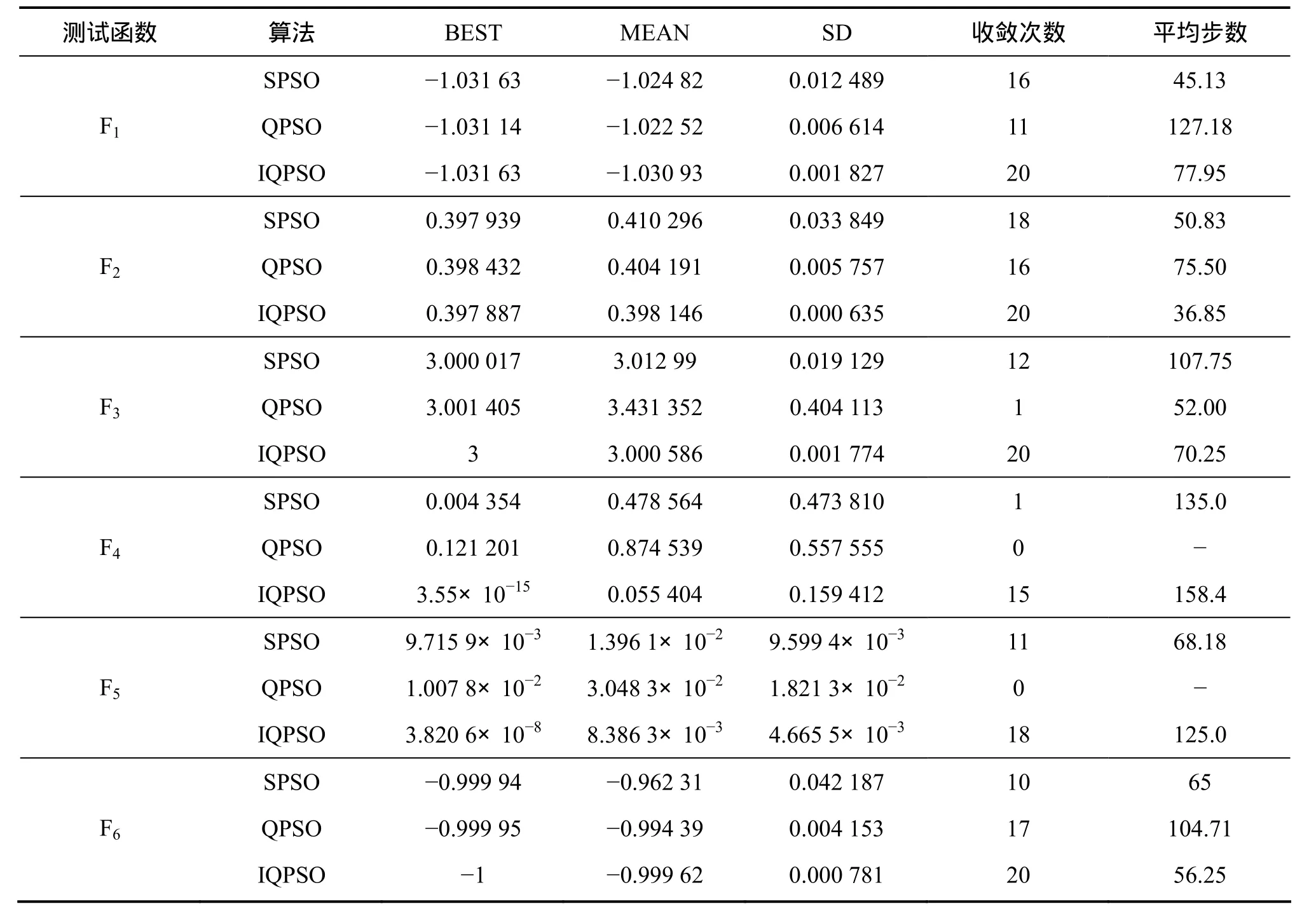
表2 3种算法对函数极值问题的优化结果对比Table 2 Comparison of optimization results between proposed algorithm and other algorithms

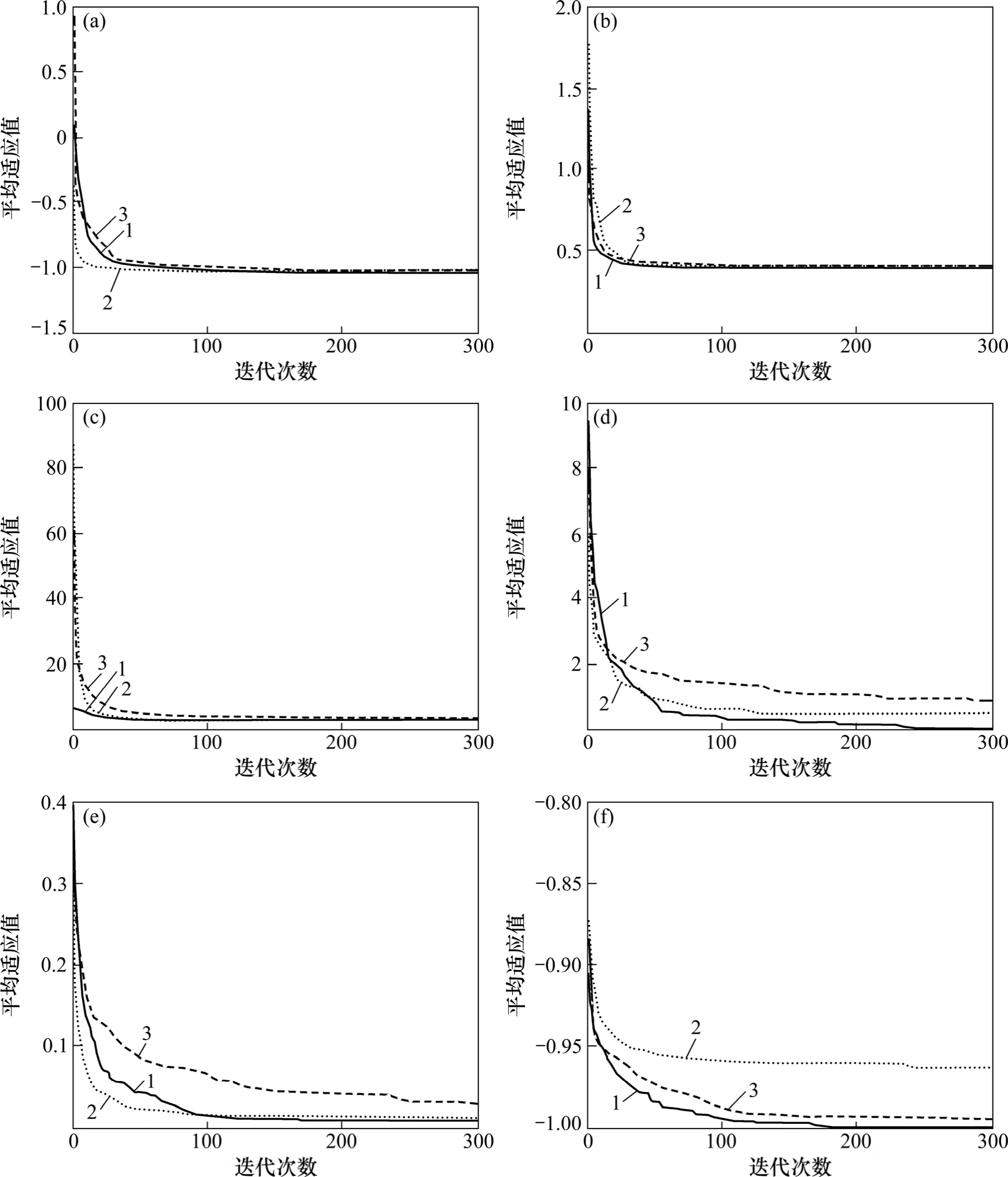
图2 测试函数收敛曲线Fig. 2 Convergence curve of test function

综合以上可见，无论是算法的收敛精度还是收敛能力，IQPSO算法都比SPSO和QPSO算法有较大的提高。引进佳点集法后，提高了初始种群的遍历性，初始种群分布更为均匀，从而提高了种群的全局寻优能力；惯性因子中引入混沌时间序列数，可以使粒子跳出局部极值点，避免早熟收敛。对于单峰函数和多峰函数，IQPSO算法都取得了相对满意的优化效果。本文提出的基于佳点集构造的改进量子粒子群算法提高了算法的全局搜索能力，算法的寻优性能得到改善。

4 结论

(1) 将引入佳点集构造初始化种群，使初始种群具有遍历性，提高了解空间的搜索能力；角速度中的惯性因子采用混沌时间序列数，可以使粒子遍历解空间，避免粒子陷入局部最优；同时，为避免粒子陷入早熟收敛，在算法中加入了变异处理。

(2) 仿真结果表明：基于佳点集构造的改进量子粒子群优化算法(IQPSO)，与标准粒子群优化(SPSO)算法和量子粒子群优化(QPSO)算法相比较，在寻优能力上，提出的算法具有快速的收敛能力，优化性能有较明显的提高。

[1] Kennedy J, Eberhart R C. Particle swarm optimization[C]//Proceedings of IEEE International Conference on Neural Networks, Piscataway, NJ: IEEE Press, 1995: 1942−1948.

[2] 曾建潮, 介婧, 崔志华. 微粒群算法[M]. 北京: 科学出版社,2004: 1−23, 116−139.

CENG Jianchao, JIE Jing, CUI Zhihua. Particle swarm optimization[M]. Beijing: Science Press, 2004: 1−23, 116−139.

[3] 李辉. 禁忌粒子群算法[J]. 陕西理工学院学报: 自然科学版,2011, 27(1): 85−90.

LI Hui. The taboo particle swarm optimization[J]. Journal of Shananxi University of Technology: Natural Science Edition,2011, 27(1): 85−90.

[4] 王波, 邰能灵, 翟海青, 等. 基于混合粒子群算法的短期负荷预测模型[J]. 电力系统及其自动化学报, 2008, 20(3): 50−55.

WANG Bo, TAI Nengling, ZHAI Haiqing, et al. Hybrid optimization method based on evolutionary algorithm and particle swarm optimization for short-term load forecasting[J].Journal of Electric Power System and its Automation, 2008,20(3): 50−55.

[5] 林楠. 一种新型的动态粒子群优化算法[J]. 计算机应用研究,2011, 28(3): 935−937.

LIN Nan. Newel dynamic particle swarm optimization algorithm[J]. Application Research of Computers, 2011, 28(3):935−937.

[6] 吴军, 李为吉. 改进的粒子群算法及在结构优化中的应用[J].陕西理工学院学报, 2006, 22(4): 36−39.

WU Jun, LI Weiji. Improved particle swarm optimization and its application to structural optimum design[J]. Journal of Shaanxi University of Technology, 2006, 22(4): 36−39.

[7] 梁昔明, 陈富, 龙文. 基于动态随机搜索和佳点集构造的改进粒子群优化算法[J]. 计算机应用, 2011, 31(10): 2796−2799.

LIANG Ximing, CHEN Fu, LONG Wen. Improved particle swarm optimization based on dynamic random search technique and good-point set[J]. Journal of Computer Applications, 2011,31(10): 2796−2799.

[8] 丁华福, 姜晓伟, 王丽雪. 基于禁忌搜索的自适应粒子群算法[J]. 计算机技术与发展, 2010, 20(4): 140−143.

DING Huafu, JIANG Xiaowei, WANG Lixue. Adaptive particle swarm optimization algorithm based on tabu search[J].Computer Technology and Development, 2010, 20(4): 140−143.

[9] 王俊伟, 王定伟. 一种带有梯度加速的粒子群算法[J]. 控制与决策, 2004, 19(11): 1298−1300.

WANG Junwei, WANG Dingwei. Particle swarm optimization algorithm with gradient acceleration[J]. Control and Decision,2004, 19(11): 1298−1300.

[10] 李士勇, 李盼池. 求解连续空间优化问题的量子粒子群算法[J]. 量子电子学报, 2007, 24(5): 569−574.

LI Shiyong, LI Panchi. Quantum particle swarms algorithm for continuous space optimization[J]. Chinese Journal of Quantum Electronics, 2007, 24(5): 569−574.

[11] Chen B R, Feng X T. Particle swarm optimization with contracted ranges of both search space and velocity[J]. Journal of Northeastern University: Natural Science, 2005, 26(5): 488−491.

[12] Shi Y, Eberhart R. A modified particle swarm optimizer[C]//IEEE International Conference on Evolutionary Computation Proceedings, Anchorage, AK: IEEE, 1998: 69−73.

[13] 华罗庚, 王元. 数论在近代分析中的应用[M]. 北京: 科学出版社, 1978: 1−99.HUA Luogeng, WANG Yuan. The application of number theory in the modern analysis[M]. Beijing: Science Press, 1978: 1−99.

[14] Yao X, Liu Y, Lin G M. Evolutionary programming made faster[J]. IEEE Transactions on Evolutionary Computation, 1999,3(2): 82−102.

(编辑 邓履翔)

Improved quantum particle swarm optimization based on good-point set

CHEN Yixiong1,2, LIANG Ximing1,3, HUANG Yafei1

(1. School of Information Science and Engineering, Central South University, Changsha 410083, China;2. Training Center, Xiangtan Iron & Steel Co. Ltd., Xiangtan 411104, China;3. School of Science, Beijing University of Civil Engineering and Architecture, Beijing 100044, China)

In order to solve the problems of premature convergence and poor local search on particle swarm optimization(PSO) algorithm, an improved quantum particle swarm optimization(IQPSO) approach was proposed. Based on quantum particle swarm optimization algorithm (QPSO), good-point set was introduced to the approach to initialize initial angle of quantum position, to improve ergodicity of initial population. To make particle jump out of local extreme value point, the chaotic time series numbers were used to update particle velocity. To prevent particle from premature convergence,mutation process was added in the approach. The simulation experiment results show that the improved algorithm has rapid convergence, good stability and it gives better performance than standard particle swarm optimization (SPSO) and quantum particle swarm optimization (QPSO).

particle swarm optimization; chaos; premature convergence; good-point set; quantum particle swarm optimization

TP301.6

A

1672−7207(2013)04−1409−06

2012−07−28；

2012−10−23

北京市自然科学基金资助项目(4122022)；湖南省教育厅项目(10C0373)

陈义雄(1974−)，男，湖南东安人，工程师，博士研究生，从事智能优化算法研究；电话：13786203764；E-mail：chenyixiong_neu@163.com