软岩巷道开挖支护的颗粒离散元模拟

廖九波 ，李夕兵 ，周子龙 ，邹洋

(1.中南大学 资源与安全工程学院，湖南 长沙，410083；2.中南大学 深部金属矿产开发与灾害控制湖南省重点实验室，湖南 长沙，410083)

随着人类对矿产资源需求量的日益增大，已使浅部资源不断减少和枯竭，国内外很多矿山相继进入深部开采，深部高应力软岩巷道开挖与支护问题也变得日益突出[1−2]。深部高应力软岩巷道一般具有如下特征：(1) 巷道埋深大、构造应力较大或受采动影响；(2) 来压时间快、持续时间长、初期变形量大；(3) 围岩较松软破碎、流变性和蠕变性较大；(4) 围岩遇水极易崩解、强度降低明显等特点。若相关措施采取不当，巷道围岩变形将越演越烈，最终致使巷道失稳破坏。因此，研究高应力软岩巷道的破坏机制和支护方式成为矿业界亟待解决的重大问题[3−8]。PFC2D 既可解决静态问题也可解决动态问题，既可用于参数预测，也可用于在原始资料详细情况下的实际模拟。Hazard等[9]应用颗粒流分析软件PFC研究了岩石材料的力学实验，发现得到的应力应变曲线与伺服控制室内试验所得结果能很好地吻合，表明离散元颗粒流软件PFC具有模拟岩石基本力学特性的能力。Wang等[10]对岩石中的开挖问题运用PFC2D进行了模拟，探讨了圆洞周围的破坏情况。本文作者以贵州开磷集团马路坪矿某巷道施工过程中出现的软弱围岩为背景，结合现场实际情况，对巷道围岩的破裂区、塑性区和弹性区进行弹塑性力学分析，探讨其应力和位移变化规律。同时，用颗粒流分析软件PFC2D对巷道支护前后围岩的位移变化进行了数值模拟，这有助于进一步研究软岩巷道的破坏变形特性和评价支护结构的效果。

1 工程地质概况及软岩特性

马路坪矿750中段某软岩巷道主要布置在红页岩中，巷道为三心拱断面。巷道所在位置总体为一单斜构造，属洋水背斜东翼，地层倾向 120°～130°，倾角30°～35°。图1所示为具有代表性的此巷道独头掘进的红页岩断面，红页岩呈明显的倾斜层状分布，下部为在潮湿空气中风化崩解脱落的红页岩碎块，从该处取回岩样标本，在地质显微镜下进行了切片分析。

样本的外观特征描述为：紫红色，层理构造，泥质结构，块状构造，矿物颗粒细小。经检验，其主要矿物成分见表1。

图1 典型红页岩断面Fig.1 Section of representative red shale

表1 红页岩的主要矿物成分(质量分数)Table 1 Major mineral components of red shale %

显微镜下，该岩石样本的结构组成如下：样品具粉砂结构，泥质结构，层理构造。填隙物含量约为55%，碎屑含量约为45%。碎屑成分主要为钾长石、白云母、绢云母、石英以及微量锆石；胶结类型为孔隙胶结；填隙物主要为绢云母、泥质物、石英、方解石和铁质物。

此类红页岩遇水极易崩解，即使在空气中也会因吸水而逐渐解体。在这种软弱岩层中施工巷道面临很大难题：围岩变形较大，支护异常困难，施工工期延长。

2 深埋软岩巷道围岩变形破坏的弹塑性力学分析

在原岩中开挖巷道，围岩应力将发生2个显著变化：一是巷道径向应力下降，周边处为零；二是切向应力增加，出现了应力集中现象。另一方面，岩体由三向应力平衡状态变成了近似二向，岩石的强度下降了。如果集中应力小于岩体强度，那么围岩将处于弹塑性稳定状态；当应力超过围岩强度之后，巷道周边围岩将首先破坏，并逐渐向深部扩展，直至在一定深度取得三向应力平衡为止，此时围岩已过渡到破碎状态[11−12]。以圆形巷道为例，巷道围岩将沿周边至纵深依次形成破碎区、塑性区和弹性区，图2所示为巷道围岩变形分区。

2.1 力学模型

现对巷道进行弹塑性力学分析，其力学模型见图3，建模做如下基本假设：

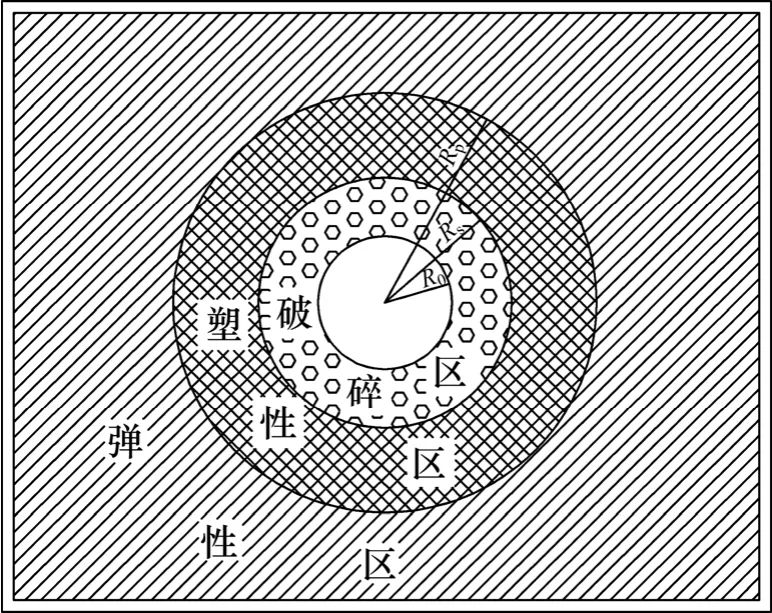
图2 巷道围岩变形分区Fig.2 Deformation layers within surrounding rock of tunnel

(1) 深埋无限长拱形平巷。

假设埋深Z大于或等于 20倍的巷道当量半径R0(或其宽、高)。当埋深Z≥20R0时，可忽略此巷道影响范围(3～5倍的R0)内的岩石自重。则在无限长的巷道长度里，围岩的性质一致，能满足弹塑性力学计算要求。所选模型可以看成平面应变问题，研究巷道任一截面的围岩分区状态。

(2) 假设围岩为理想弹塑性体。

(3) 假设原岩应力为各向等压的静水压力。

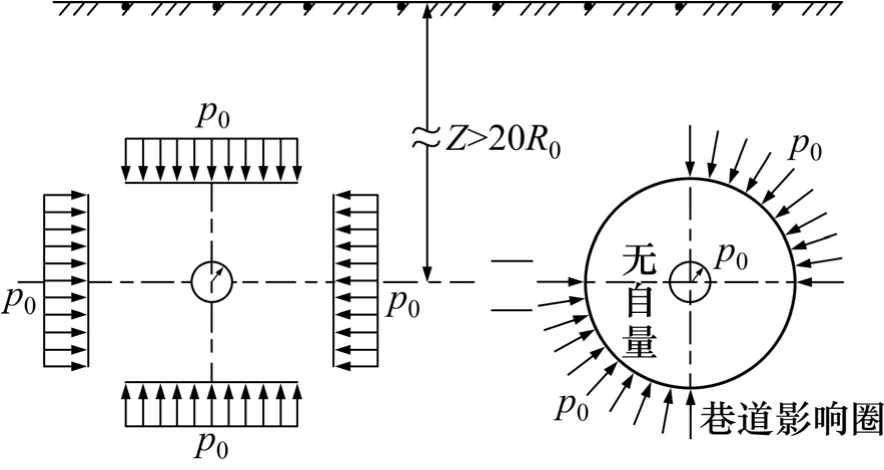
图3 深埋圆形巷道力学模型Fig.3 Mechanical model of deep circular tunnel

2.2 巷道围岩弹塑性位移解

弹塑性边界的位移由弹性区的岩体变形引起，弹性区的变形可按外边界趋于无穷、内边界为Rp的厚壁圆筒来处理。

根据弹塑性力学中的平衡方程、几何方程、本构方程和边界条件，并利用岩石库伦准则可计算得到在无支护时圆形巷道周边的位移公式[13]为：

由于拱形巷道围岩位移公式缺乏精确的理论解，故采用当量半径折算法，任意形状巷道尺寸折算成圆形巷道表示如下：

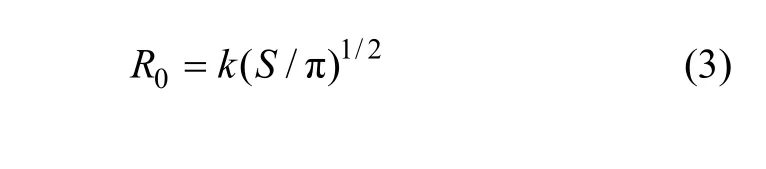
式中：R0为巷道当量半径；k为断面形状修正系数，拱形取1.1；S为实际巷道断面积。

图4所示为拱形巷道力学模型。

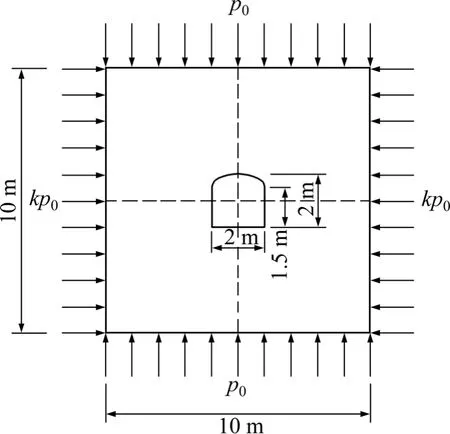
图4 拱形巷道力学模型Fig.4 Mechanical model of arched tunnel

由图4可见：马路坪红页岩拱形巷道拱宽为2 m，拱高0.5 m，直墙高1.5 m，可算得拱形巷道面积S为3.79 m2，进而巷道当量半径：

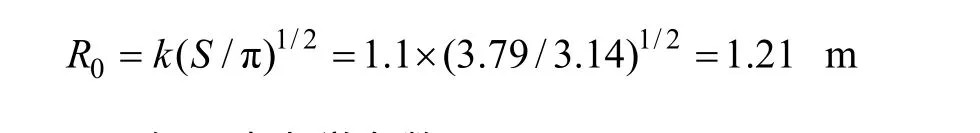
现取红页岩力学参数：E=1 522 MPa，ν=0.33，p0=20.67 MPa，c=2.12MPa，φ=43°。利用式(2)，可算此拱形巷道围岩塑性区半径为：

巷道断面的收缩量是0.22 m2，约占巷道总面积的5.7%。可见围岩只要处于完整状态，其变形量相对较小。

从上述弹塑性区的变形求解公式分析可知：红页岩巷道开挖后变形量较大，需要立即对巷道进行支护，也就是临时支护，其作用一是封闭围岩，防止具有膨胀性围岩吸水弱化，二是改变巷道围岩的应力状态，防止巷道围岩破碎区的进一步扩展。马路坪矿目前采取的支护措施是先挂网后喷浆，这种做法是不尽妥当的，要先喷浆再挂网打锚杆，在巷道变形前及时地喷浆能很好地起到封闭围岩的作用。

3 巷道开挖与支护的颗粒流模拟

3.1 颗粒流软件PFC2D简介

PFC2D采用离散单元法能直接模拟球形颗粒间的运动和相互作用的物理问题，适用于研究固体材料的细观/宏观裂纹扩展、破坏累积并断裂、破坏冲击和微震响应等问题。同时，PFC2D内置接触模型包括：简单的黏弹性模型、简单的塑性模型以及位移软化模型。因此，PFC2D颗粒流程序也适用于模拟固体材料的弹塑性力学问题。

PFC2D模型中离散的颗粒单元不断进行平移和旋转运动，分离的颗粒在计算过程中又可重新形成新的接触。颗粒流方法的理论基础是力−位移定律和牛顿第二定律，采取显式时步循环运算规则对圆形颗粒进行循环计算。根据力−位移定律确定 2个实体(颗粒−墙体或颗粒−颗粒)间的相对运动，并计算其间的接触力。根据牛顿第二定律计算每个颗粒由于体积力或接触力变化引起的颗粒运动(速度和位置)。

用PFC2D本身自带的FISH语言，PFC2D程序在宏观方面可以监测模型的宏观应力−应变关系、局部位移及表面裂隙的扩展情况，细观方面可以观察到模型内部各点的应力−应变关系、接触力、速度、裂纹及应变能等物理量的变化[14−15]。

3.2 数值分析模型

为了使模拟结果更接近实际情况，需选取合理的颗粒体细观参数，首先做红页岩试样单轴抗压试验(见图 5)，得到其单轴应力−应变曲线(见图 6)，然后用PFC2D建立岩石单轴抗压数值模型，分析模型中细观参数对宏观性质的影响，不断试算得到与红页岩单轴抗压试验值基本一致的力学模型的细观参数，当数值模型与室内实验两者所得的单轴应力−应变曲线能最大程度地吻合，表明此时的细观参数可用来模拟该巷道开挖引起的围岩破坏，其基本细观参数取值见表2。

根据实际工程情况，取马路坪矿750中段某软岩巷道断面作为模拟断面，数值计算采用PFC2D建立二维数值模型，共定义上、下、左、右4道墙体，模型宽10 m，高10 m，颗粒半径服从高斯分布。固定模型下部边界，对上部边界施加与覆岩厚度相应的垂直应力，对两侧边界分别施加相应的水平应力。对模型施加的水平应力和垂直应力均为2.067×107N/m2，此时侧压力系数k为1，即静水压力状态。

图5 红页岩试样单轴抗压试验Fig.5 Uniaxial compressive test of red shale sample

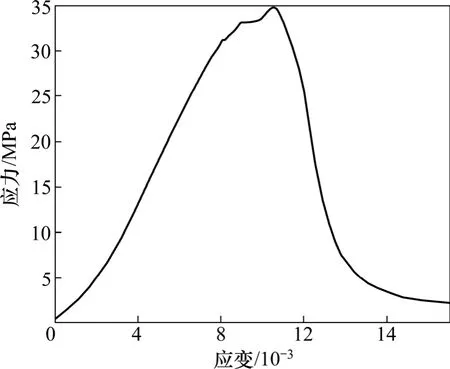
图6 室内单轴应力−应变曲线Fig.6 Stress−strain curve by laboratory uniaxial test

表2 PFC2D数值模拟参数Table 2 PFC2D numerical simulation parameters

颗粒流模型重力平衡后，挖去中间拱形巷道的部分颗粒，模拟拱形巷道开挖。颗粒流模型的颗粒数目为70 028个，共挖去2 673个颗粒，剩余67 355个颗粒。巷道的数值模型见图7。

拱形巷道参数如下：宽度2.0 m，直墙高1.5 m，拱高0.5 m，其中心点坐标x0=5.0，y0=5.0，即为模型正中心。

图7 巷道的数值模型Fig.7 Numerical model of tunnel

3.3 计算结果分析

图8所示为开挖后无支护巷道拉应力分布。先研究巷道未支护情况下的围岩稳定性，巷道围岩在开挖前都是以压应力为主，但在开挖后许多关键部位应力集中比较明显，出现了较大的拉应力，巷道顶部、底部和两帮数值较大(见图 8)，其最大拉应力值分别为0.28，0.53和0.47 MPa，说明这些区域易受开挖的影响，由于岩体抗拉强度很小，易导致巷道围岩受拉伸破坏。这些拉应力集中的关键部位，不利于巷道的稳定，易出现较大破坏，应在最佳支护时间段内加强支护。

图8 开挖后无支护巷道拉应力分布Fig.8 Tensile stresses distribution of unlined tunnel after excavation

图9所示为拱形巷道围岩无支护时开挖引起的位移场示意图。由图9可见：高应力软岩巷道受开挖和原岩应力场的影响，拱顶、拱底及两侧的位移较大，说明这些位置受开挖的影响较大，而左上、左下、右上和右下4个角点处位移较小。位移最大值发生在拱底的位置，其值达到33.43 mm，易出现地压底鼓现象。在深井软岩中，顶板下沉量、底鼓量和两帮移近量是整个巷道变形量的主要部分，在进行支护设计时主要就是控制巷道围岩的这3种变形。数值模拟结果表明，软岩巷道开挖后，应尽早地进行支护以便有效地控制围岩的变形[16]。数值模拟中开挖后不支护所得巷道围岩表面位移平均为29.99 mm，而前文弹塑性理论分析解为28.46 mm，两者误差仅为5.11%，可见数值模拟和理论分析两者结果比较一致，进一步证明基本模型正确，进而利用模型模拟巷道支护问题，找到支护效果随支护时间的变化规律。图10所示为拱形巷道围岩喷射混凝土和锚杆支护时位移场示意图。由图 10可见：支护已经起到了明显效果，减少了围岩的位移量。

图9 无支护时位移场Fig.9 Displacement field in case of no liner

下面分别研究无支护和有支护2种工况下的围岩位移变化规律，对支护效果进行评价。若开挖不及时采取支护措施将导致巷道围岩出现不稳定现象，在现场施工中应在开挖后尽早地开展支护工作。在计算分析过程中，将巷道竖向中心线选作轴线，模型具有左右对称特性。现取巷道左侧的围岩分析，在其中布置5个测量点，分别对拱顶、左上角、左拱腰、左下角、拱底处的围岩位移发展状况进行监测，以此得到对应的位移来说明支护前后软岩巷道围岩的变形[17]。因为无法在开挖时就对危岩进行支护，支护总是在开挖一段时间之后才进行。在数值模拟过程中，这点表现在支护之前，围岩在自重作用下已经发生了径向位移。因此，分别做了开挖后时间分别为1 000，2 000，3 000，4 000，5 000，6 000和7 000步才开始支护的模拟，得到了一些结论。在支护这项数值模拟中，利用了 2种支护措施：喷射混凝土层厚度0.4 m，采用接触连结；布置5根长1.5 m的锚杆，分别与x轴正方向成30°，60°，90°，120°和 150°，本文喷射混凝土层采用小颗粒模拟，由于墙体尺寸有限，一次生成颗粒厚度较小，为此进行两次颗粒生成以增加喷浆的厚度。锚杆体由定义为刚性重叠连接的圆形大颗粒组成，定义颗粒的黏结强度、密度、直径等指标，采用Clump命令，使颗粒相互重叠连接，形成锚杆体。模型中衬砌支护结构的力学参数见表3。

图10 支护时位移场Fig.10 Displacement field in case of liner

现选取巷道开挖后时间为3 000步才开始支护为代表来说明问题，图11～13所示分别为拱顶的竖向位移、左拱腰水平位移和拱顶的竖向位移随时步的变化规律。由图11～13可以看到：2种工况下巷道围岩在1万步左右时基本稳定，现场观测马路坪矿该软岩巷道在开挖1月后变形基本稳定，将模型中时间步数换算成实际时间，发现与现场情况基本相符。

从图11～13可以发现：无论是底鼓量、两帮移近量和顶板沉降量都有开挖初期变形量大，增长速率高，它们的增长速率会随时间的增加而逐渐降低，最后曲线渐渐趋向于水平达到稳定平衡。从图11可以看出：软岩巷道拱顶竖向位移随时间的变化规律，开挖造成的位移有28.74 mm，支护之后位移只有22.12 mm，采用支护措施后位移减小了6.62 mm，说明支护在抑制围岩变形方面起到了一定的作用。图12中，支护前左拱腰水平位移为27.82 mm，支护后，位移只有20.95 mm，减少了 6.87 mm，表明支护起到了作用。从图13可以看出：支护前拱底的竖向位移为33.43 mm，而采用支护等措施后，位移仅发展了26.40 mm，拱底的竖向位移得到了控制。若在最佳支护时间对围岩施加最优的支护措施，能进一步缩减围岩的变形量。

以上只对开挖后时间为3 000步进行支护的情况开展了讨论，为了能充分说明支护快慢影响位移值大小，有必要对巷道开挖后若干不同时步才支护的围岩位移变化情况分别予以模拟。为此，整理出各监测圈最终位移随不同支护时步的变化规律如表4所示，最终位移随不同支护时步的曲线如图14所示。可见：开挖至支护的时间步数越少，即时间越短，拱顶、左拱腰和拱底的最终位移值将会越小，在高应力软岩巷道开挖时，应尽早进行支护加固工作[18]。围岩表面位移最大值发生在拱底的位置，此处易出现地压底鼓现象，应加强支护。

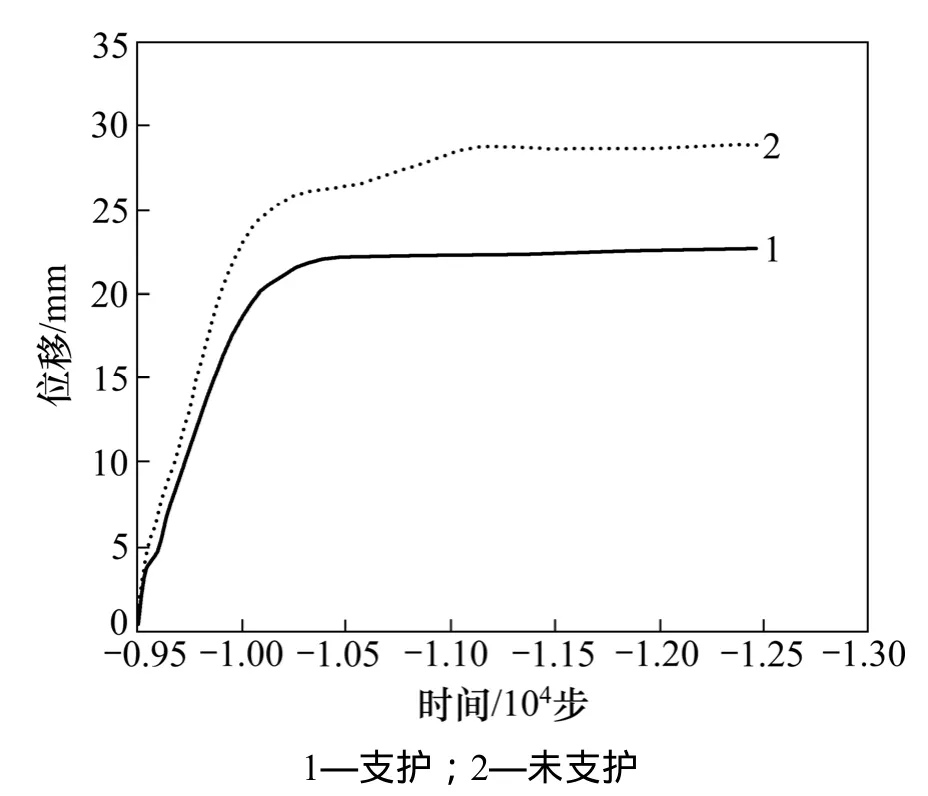
图11 拱顶竖向位移曲线Fig.11 Curve of vertical displacement for vault

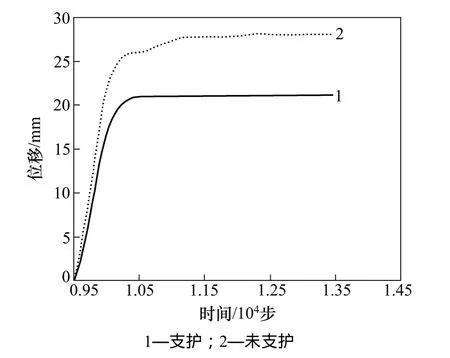
图12 左拱腰水平位移曲线Fig.12 Curve of horizontal displacement for left hance

表3 衬砌支护结构的力学性能Table 3 Mechanical properties for liner and timbering

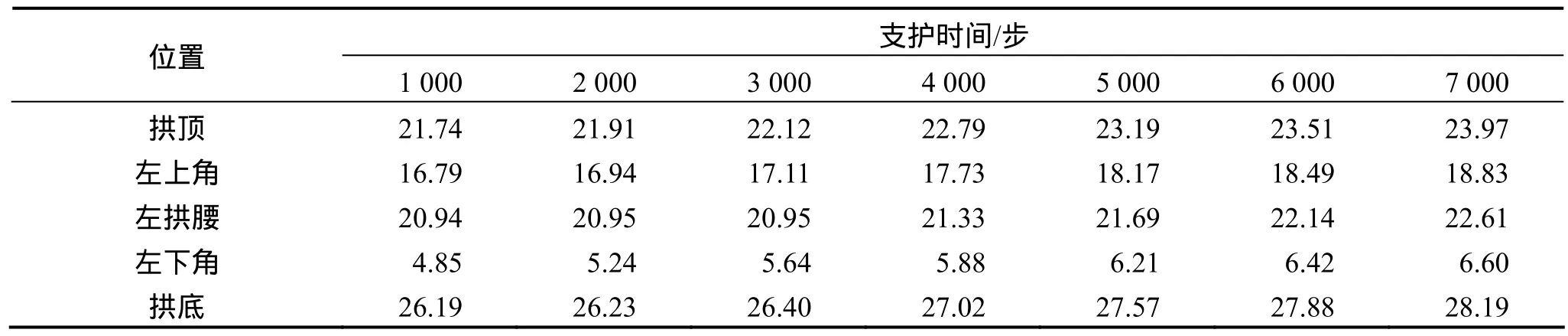
表4 各监测圈最终位移随不同支护时步的变化Table 4 Variation of final displacement of every monitored circles versus different steps of lining mm

图13 拱底竖向位移曲线Fig.13 Curve of vertical displacement for arch foot

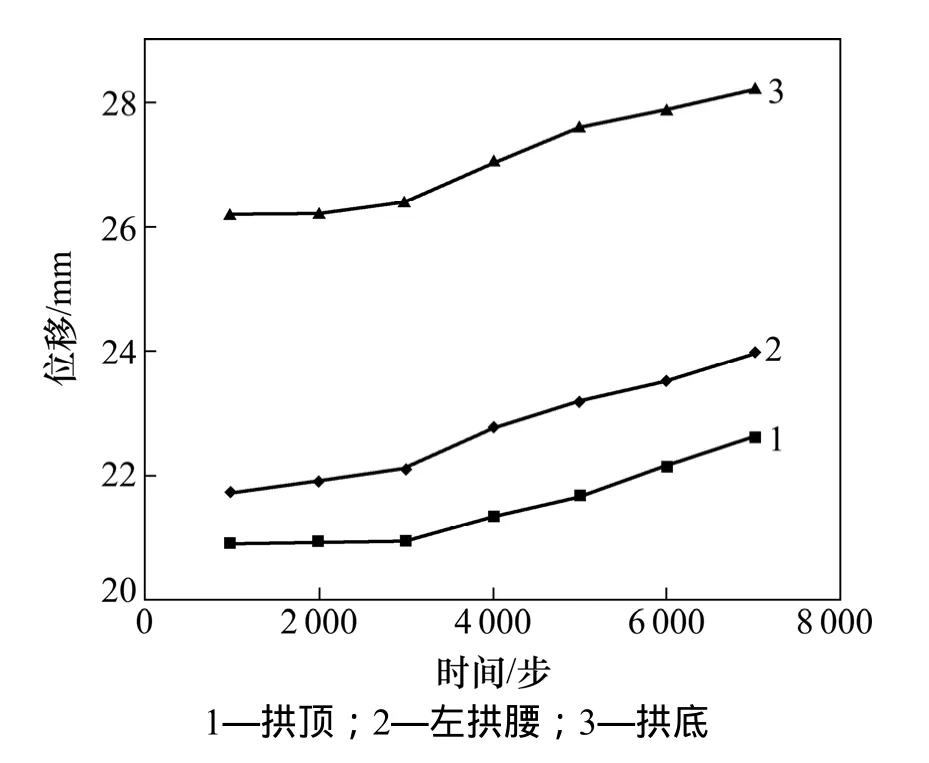
图14 最终位移随不同支护时步的曲线Fig.14 Curve of final displacement versus different steps of lining

4 结论

(1) 根据理想弹塑性模型中的变形协调条件、基本方程和相应的边界条件，并利用岩石强度理论—库仑准则，将巷道围岩分成弹性区、塑性区和破裂区，并建立了在特定原岩应力条件下软岩拱形巷道开挖后的围岩位移解析表达式。

(2) 用颗粒流分析软件PFC2D对软岩巷道开挖后围岩变形破坏规律进行了数值模拟，可以清晰地看到软岩巷道在开挖后的应力分布情况，详细探讨了围岩各个关键部位的位移分布特征，所获巷道表面位移与弹塑性解比较一致，证明基本模型正确，进而利用模型模拟巷道支护，找到支护效果随支护时间的变化规律，结果表明开挖后支护时间越早，越能控制围岩变形量。所获研究结论，可为复杂应力条件下类似巷道的变形研究和支护设计提供理论依据。

(3) 分别运用弹塑性力学理论和PFC2D数值模拟得到了马路坪矿特定红页岩巷道围岩表面的位移变形量，位移最大值发生在拱底的位置，其值达到 33.43 mm，易出现地压底鼓现象，应尽早地进行支护以便有效地控制围岩变形。

[1] 古德生, 李夕兵.有色金属深井采矿研究现状与科学前沿[J].矿业研究与开发, 2003, 23(2): 1−5.GU Desheng, LI Xibing.Science problems and research state of deep mining in metal and nonferrous mines[J].Mining research and development, 2003, 23(2): 1−5.

[2] 李夕兵, 古德生.深井坚硬矿岩开采中高应力的灾害控制与破碎诱变[C]//科学前沿与未来(第6集).北京: 中国环境科学出版社, 2002: 101−108.LI Xibing, GU Desheng.The hazard control and cataclastic mutagenesis induced by high stress in hard rock mining at depth[C]//Science Foreland and Future(Volume 6).Beijing:China Environmental Science Press, 2002: 101−108.

[3] 何满潮, 景海河, 孙晓明.软岩工程力学[M].北京: 科学出版社, 2002: 38−45.HE Manchao, JING Haihe, SUN Xiaoming.Engineering mechanics of soft rock[M].Beijing: Science Press, 2002: 38−45.

[4] Sellers E J, Klerck E.Modeling of the effect of discontinuities on the extent of the fracture zone surrounding deep tunnels[J].Tunneling and Underground Space Technology, 2000, 15(4):463−469.

[5] Russo-Bello F, Murphy S K.Longwalling at great depth in a geologically disturbed environment.the Way forward[J].The Journal of South African Institute of Mining And Metallurgy,2000, 100(2): 91−100.

[6] 王连国, 李明远, 王学知.深部高应力极软岩巷道锚注支护技术研究[J].岩石力学与工程学报, 2005, 24(16): 2889−2893.WANG Lianguo, LI Mingyuan, WANG Xuezhi.Study on mechanisms and technology for bolting and grouting in special soft rock roadways under high stress[J].Chinese Journal of Rock Mechanics and Engineering, 2005, 24(16): 2889−2893.

[7] 王其胜, 李夕兵, 李地元.深井软岩巷道围岩变形特征及支护参数的确定[J].煤炭学报, 2008, 33(4): 364−367.WANG Qisheng, LI Xibing, LI Diyuan.Surrounding rock deformation properties and determination of support parameters of soft rock roadway in deep mine[J].Journal of China Coal Socitey, 2008, 33(4): 364−367.

[8] 杨新安, 陆士良, 葛家良.软岩巷道锚注支护技术及其工程实践[J].岩石力学与工程学报, 1997, 16(2): 171−176.YANG Xinan, LU Shiliang.GE Jiahang.The technology and practice of bolting and grouting support method at soft rock roadway[J].Chinese Journal of Rock Mechanics and Engineering, 1997, 16(2): 171−176.

[9] Hazard J F, Young R P.Simulating acoustic emissions in bonded-panicles models of rock[J].International Journal of Rock Mechanics and Mining Sciences, 2000, 37(5): 867−872.

[10] Wang C, Tannant D D, Lilly P A.Numerical analysis of the stability of heavily jointed rock slopes using PFC2D[J].International Journal of Rock Mechanics and Mining Science,2003, 40(3): 415−424.

[11] 蒋斌松, 张强, 贺永年, 等.深部圆形巷道破裂围岩的弹塑性分析[J].岩石力学与工程学报, 2007, 26(5): 982−986.JIANG Binsong, ZHANG Qiang, HE Yongnian, et a1.Elastoplastic analysis of cracked surrounding rocks in deep circular openings[J].Chinese Journal of Rock Mechanics and Engineering, 2007, 26(5): 982−986.

[12] Sharan S K.Exact and approximate solutions for displacements around circular openings in elastic-brittle-plastic Hock-Brown rock[J].Int J Rock Mech Min Sci, 2005, 42(4): 542−549.

[13] Kyung H P, Yong J K.Analytical solution for a circular opening in an elastic-brittle-plastic rock[J].Int J Rock Mech Min Sci,2006, 43(4): 616−622.

[14] ITASCA Consulting Group lnc.PFC2D theory and background[M].Minnesota: Itasca Consulting Group Inc, 2008:25−86.

[15] 徐泳, 孙其减, 张凌, 等.颗粒离散元法研究进展[J].力学进展, 2003, 33(2): 25l−260.XU Yong, SUN Qicheng, ZHANG Ling, et a1.Advances in particle discrete element methods[J].Advances in Mechanics,2003, 33(2): 25l−260.

[16] Funatsu T, Hoshino T, Sawae H, et al.Numerical analysis to better understand the mechanism of the effects of ground supports and reinforcements on the stability of tunnels using the distinct element method[J].Tunneling and Underground Space Technology, 2008, 23(3): 561−573.

[17] 陶连金, 蒯本秋, 张波.松散软岩巷道破坏的颗粒离散元模拟分析[J].地下空间与工程学报, 2010, 6(2): 318−322.TAO Lianjin, KUAI Benqiu.ZHANG Bo.PFC the fracture mechanism analysis of loose soft roadway by discrete element method[J].Chinese Journal of Underground Space and Engineering, 2010, 6(2): 318−322.

[18] 孟云伟, 肖世洪, 柴贺军, 等.隧道开挖中破碎带支护的颗粒离散元模拟研究[J].地下空间与工程学报, 2007, 3(4):673−677.MENG Yunwei, XIAO Shihong, CAI Hejun, et al.PFC Simulation of timbering in fragment strip during tunnel excavation[J].Chinese Journal of Underground Space and Engineering, 2007, 3(4): 673−677.