轴套形状误差的过盈配合映射研究

潘旭辉

(中国航空工业洛阳电光设备研究所，河南洛阳 471009)

轴套形状误差的过盈配合映射研究

潘旭辉

(中国航空工业洛阳电光设备研究所，河南洛阳 471009)

过盈联接大量应用于轴承与轴类的联接中。对于精密类仪器，分析机械加工形状误差对过盈配合精度的影响十分重要。使用有限元分析软件ANSYS对带有形状误差的轴套过盈配合进行有限元仿真。分析轴套形状误差、过盈量与套圈外径的映射关系。结果表明：在过盈量与误差值一定，轴与套圈内径有相同的误差棱圆边数时，无量纲化的变形量幅值最小;在过盈量与形状误差一定，轴与套圈内径的误差值相同时，无量纲化的变形量幅值最小，趋近于零;在误差形状和误差值不变的情况下，随着过盈量的增大，无量纲化的变形量幅值呈现递减趋势。

过盈配合;形状误差;变形量;有限元分析

0 引言

过盈联接结构简单、可靠、定心性高、抗冲击性好，是工程中常见的一种结构联接方式，例如机车的轴过盈联接，滚动轴承的内圈与轴的配合也属于过盈联接等。对于精密类仪器，如机床、雷达等，机械部分的加工精度对过盈配合件的精度有很大影响，而且机械加工形状误差本身是不可能完全消除的，所以分析机械加工形状误差对过盈配合精度的影响十分重要。

很多学者对过盈配合进行过研究，如刘晓初等人［1-2］用经典的弹性力学理论来分析轴套过盈配合时过盈量与接触应力和接触变形的关系。但经典的弹性力学方法无法分析轴套形状误差的过盈配合。周鹤群等人［3-8］用有限元方法分析过盈配合时接触应力的变化规律。但他们更多的是研究过盈配合时力的传递路线，没有研究变形的传递路线，也没有研究轴套形状误差对其精度的影响。

本文用有限元软件ANSYS对轴套形状误差的过盈配合进行有限元仿真。首先对有限元模型进行灵敏度分析，验证其是否可以模拟零件的形状误差。其次利用偏移节点坐标的方法来模拟零件的形状误差。对有限元模型进行仿真，分析轴套形状误差、过盈量与套圈外径的映射关系，对实际工程计算具有一定的参考意义。

1 过盈配合的弹性理论分析

轴套过盈配合问题可以简化为内半径为ra，外半径为rb的组合厚壁圆筒。如图1所示，由两层圆筒套装而成，内筒的外半径为(rb+δ1)，内半径为ra，外筒的外半径为rc，内半径为(rb－δ2)。

图1 组合厚壁圆筒

套装后在两个圆筒的接触表面将产生均匀的压应力，即套装压力。套装压力的大小与过盈量有关，两个套筒的过盈量就是他们的径向位移。对于平面应力问题，根据弹性力学［9］厚壁圆筒理论公式，对于内筒，其外半径处的径向位移:

其中，δ0= － δ1+ δ2——组合厚壁圆筒的过盈量，E——材料的弹性模量，λ——材料的泊松比。

2 过盈配合的有限元分析

2.1 灵敏度分析

轴套零件的基本结构参数如表1所示。材料属性见表2。

表1 轴套零件的基本结构参数(单位:mm)

表2 材料属性

由于轴套零件的形状误差一般在几个μm，用有限元模拟形状误差时要对其灵敏度进行分析。选取接触变形±0.005μm理论值作为灵敏度分析的评价指标。进行灵敏度分析时不考虑轴套零件的形状误差。

在进行灵敏度分析时，由于不考虑轴套的形状误差，且本文所采用的实体模型为轴对称形状，为了减少计算时间，模型只取原模型的1/4进行分析。为了减少重复操作软件的工作量，使用ANSYS的APDL语言［10］编制整个分析过程。

本文用施加温度载荷的方法来模拟过盈配合的过盈量。ANSYS根据下式计算结构热应变［11］:

式中:T——单元计算温度;TREF——热应变为零时的温度;αse(T)——温度相关的割线热膨胀系数;εth——热应变。

本文用二维有限元模型进行分析，采用平面八节点单元plane82，参考温度Tref=0℃。半径方向过盈量12μm，根据(4)式计算得 T=29.814℃。轴的外径为接触面，套圈内径为目标面。接触单元选择2D3节点面面元CONTA172，目标单元选择2D目标元TARGE169。接触类型选择面－面接触。约束形式采用对称约束。每段圆弧划分60份时有限元网格划分及约束如图2所示。

图2 有限元网格划分及约束

对有限元模型进行求解分析，图3是套圈的径向变形图。

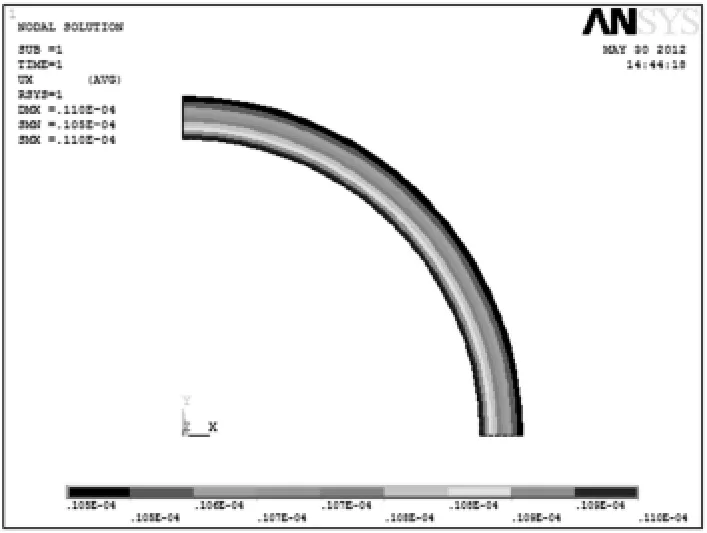
图3 套圈的径向变形图

改变模型网格划分的尺寸，进行灵敏度分析，图4是接触线径向变形量灵敏度分析结果图。

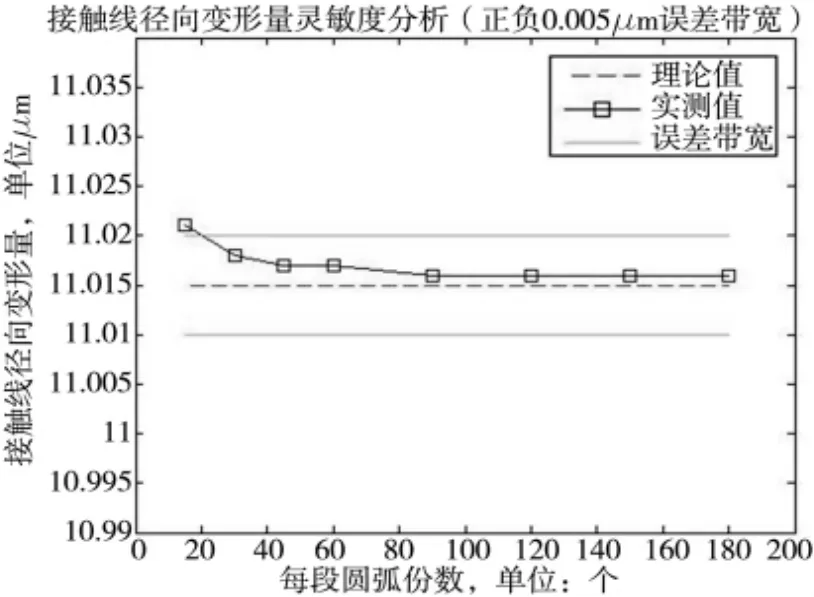
图4 接触线径向变形量灵敏度分析

注:理论值是指用弹性力学圆筒受均布压力理论计算的结果。

通过分析结果可知，当每段圆弧划分的份数达到30份时，ANSYS有限元仿真分析能满足精度要求。

2.2 形状误差的理论分析

轴套制造误差形状假定为同径不同心的n棱圆时，图5是误差分析示意图。

图5 误差分析示意图

图5中，R——圆心偏移后理论的半径;r——原始的半径;a——圆心偏移的距离;δ——制造误差;θ——R与 a的夹角;β——与棱圆边数 n有关的角度。n棱圆误差中，每段n棱圆占据1/n个圆周。即初始每段n棱圆的角度为360/n度。

首先根据图5的几何关系

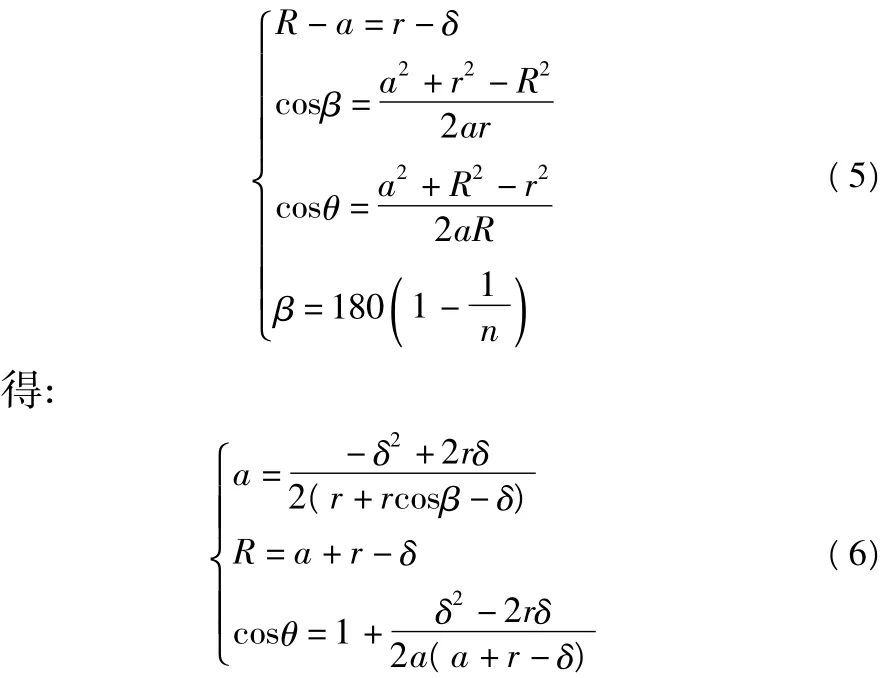
因为 r，δ是已知量，所以能求出 a，R，θ。

利用偏移节点坐标来模拟轴与套圈的误差形状，根据a能求出圆心偏移量，根据R能求出偏移后的圆弧半径，根据θ角和每段圆弧上的节点数能求出在柱面坐标系下节点偏移的角度。

2.3 模型建立及分析

利用ANSYS建模型时，套圈内径69.978mm，套圈外径80mm，轴外径69.958mm。这样建模的好处是轴外径与套圈内径在半径方向上有10μm的距离，当模拟轴与套圈在半径方向上的误差时，偏移后套圈上节点与轴上节点不干涉。

材料属性及单元类型等同灵敏度分析时一致。通过灵敏度分析知当每段长边分为30份时能够满足要求。现将每段长边分成60份，圆周线上一共分成240份，共480个节点，两两节点间的夹角是360/480=0.75度。模型共有38881个节点，13200个单元。

要正确模拟过盈量，首先要计算出轴的膨胀量δp与轴误差δz、套圈误差δk、过盈量 u和轴与套圈距离s的关系。根据几何关系得:

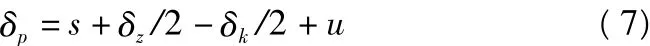
根据式(4)和(7)可求得不同误差跟过盈量下所施加的温度载荷T。温度载荷汇总见表3。

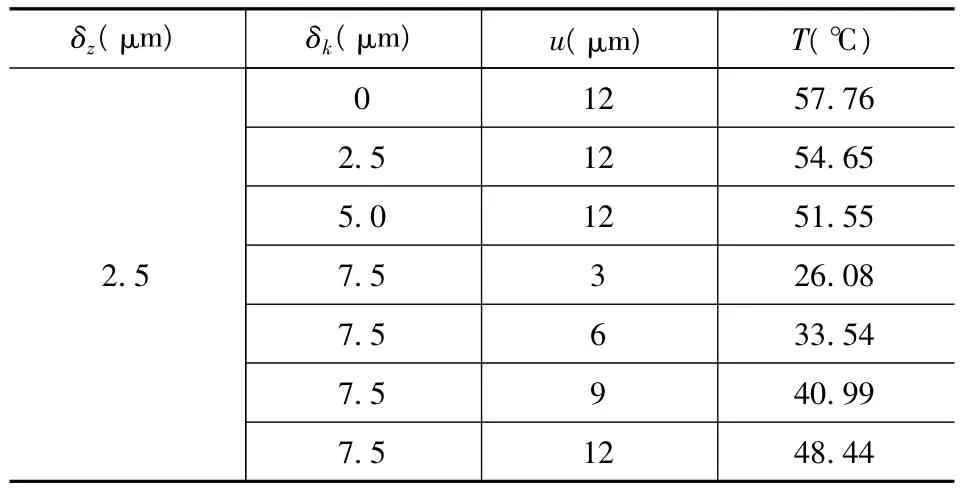
表3 轴上施加的温度载荷

对轴上中间节点进行全约束，对其附近四个节点限制旋转约束，对内圈上四个节点限制旋转约束，有限元网格划分及约束如图6所示。

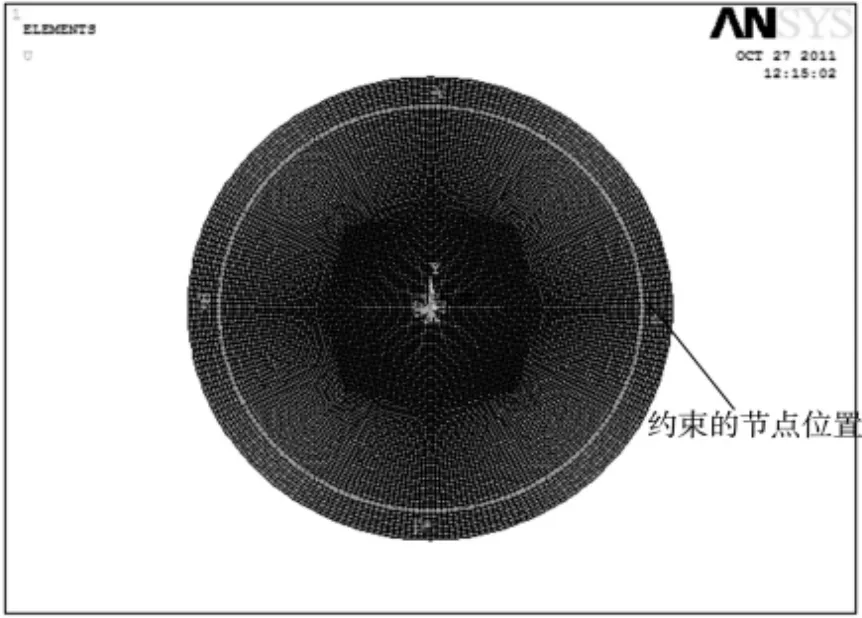
图6 有限元网格划分及约束

然后求解得到的在柱面坐标系下的径向变形量。图7是轴有2.5μm三棱圆误差，套圈内径有7.5μm三棱圆误差，过盈量12μm时套圈的径向变形图。

图7 套圈的径向变形图

3 过盈配合轴套形状误差的映射关系

误差的组合形式太多，由于文章篇幅所限，这里只讨论轴与套圈都有三棱圆误差时，套圈外径的径向变形量。本文对结果数据进行了无量纲化处理，横轴代表位置角，纵轴代表套圈外径的径向变形量与过盈量的比值，即无量纲化的套圈外径径向变形量。

3.1 误差偏角的影响分析

本节讨论轴有 2.5μm三棱圆误差，过盈量12μm，套圈内径7.5μm三棱圆误差，套圈相对于轴偏转0－30－60－90度时，不同的相对偏角对套圈外径径向变形量的影响。图8是不同偏转角度时无量纲化的变形量与位置角的关系。

从图8可以看出，在过盈量及误差值不变的情况下，随着位置角的不同，无量纲化的变形量呈周期性波动，轴与套圈相对偏转0度时，无量纲化的变形量幅值最小，偏转60度时，无量纲化的变形量幅值最大。

图8 不同偏转角度时无量纲化的变形量

3.2 误差形状的影响分析

本节讨论轴有 2.5μm三棱圆误差，过盈量12μm，套圈内径7.5μm误差，套圈内径分别是二棱圆、三棱圆、四棱圆、五棱圆误差时，不同的套圈内径误差形状对套圈外径径向变形量的影响。图9是不同误差形状时无量纲化的变形量与位置角的关系。

图9 不同误差形状时无量纲化的变形量

从图9可以看出，在过盈量及误差值不变的情况下，随着位置角的不同，无量纲化的变形量呈周期性波动，其周期数与套圈内径误差的周期数相同。套圈内径是五棱圆误差形状时，无量纲化的变形量幅值最大，套圈内径是三棱圆误差形状时，无量纲化的变形量幅值最小。相同条件下，轴与套圈内径误差的棱圆数相同时，无量纲化的变形量幅值最小。

3.3 误差值的影响分析

本节讨论套圈内径误差值对套圈外径径向变形量的影响。本部分中轴有2.5μm三棱圆误差，过盈量12μm，套圈内径有三棱圆误差，分别取误差值0μm、2.5μm、5.0μm、7.5μm 时进行分析，图 10 是套圈内径取不同误差值时无量纲化的变形量与位置角的关系。

图10 不同误差值时无量纲化的变形量

从图10可以看出，在过盈量及误差形状不变的情况下，随着位置角的不同，无量纲化的变形量呈周期性波动。随着套圈内径误差值的增大，无量纲化的变形量幅值先减小后增大，套圈内径有2.5μm误差时，无量纲化的变形量幅值最小，趋近于零。套圈内径有7.5μm误差值时，无量纲化的变形量幅值最大。

3.4 过盈量的影响分析

本节讨论过盈量对套圈外径径向变形量的影响。本部分中轴有2.5μm三棱圆误差，套圈内径有7.5μm的三棱圆误差，分别取不同过盈量时进行分析，图11是套圈内径取不同过盈量时无量纲化的变形量与位置角的关系。图12是套圈内径取不同过盈量时无量纲化的变形量和过盈量的关系。

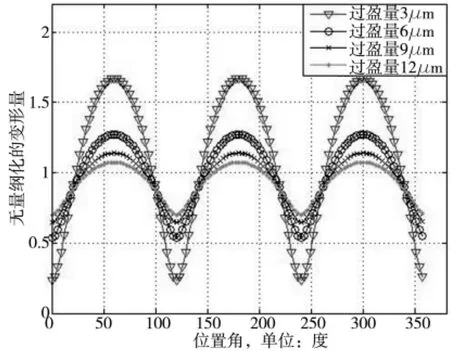
图11 不同过盈量时无量纲化的变形量与位置角关系

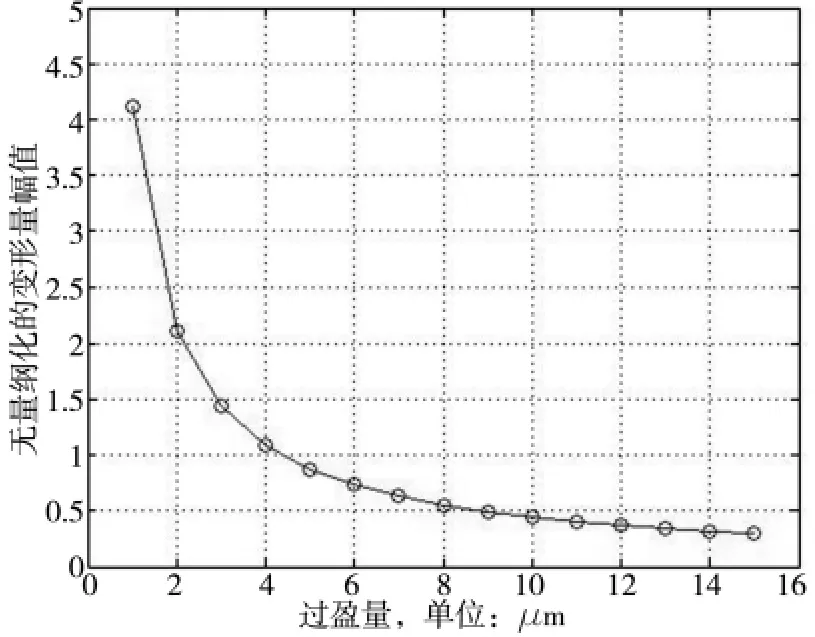
图12 无量纲化的变形量幅值与过盈量关系

从图11和图12可以看出，在误差形状和误差值不变的情况下，随着位置角的不同，无量纲化的变形量呈周期性波动。随着过盈量的增大，无量纲化的变形量幅值呈现递减趋势。

4 结论

本文运用有限元的方法，通过偏移有限元模型节点坐标模拟轴套形状误差，计算和分析了过盈配合时轴套形状误差对配合件精度的影响，发现以下规律:

(1)通过进行灵敏度分析，证明可以用偏移节点坐标的方法来模拟轴套形状误差;

(2)在过盈量与轴和套圈误差值一定时，轴与套圈内径有相同的误差棱圆边数时，无量纲化的变形量幅值最小;

(3)在过盈量与形状误差一定时，轴与套圈内径的误差值相同时，无量纲化的变形量幅值最小，趋近于零。

(4)在误差形状和误差值不变的情况下，随着过盈量的增大，无量纲化的变形量幅值呈现递减趋势。

［1］刘晓初.有效过盈量对轴承径向工作游隙的影响［J］.轴承，1996(11):11－12.

［2］张敬佩，李初晔.过盈配合产生的接触应力和拔出力计算［J］.机械工程与自动化，2011(1):195－197.

［3］周鹤群，汪中厚，谢云波.基于FEA的传动轴过盈配合精密分析［J］.机械传动，2010(1):60－65.

［4］曾飞，陈光雄，周仲荣.基于ANSYS的轮对过盈配合微动分析［J］.机械工程学报，2011(3):121－125.

［5］谭小东，李莉.盘轴过盈配合的ANSYS分析［J］.机械研究与应用，2011(4):30－31.

［6］安吉阁，李建宾，等.基于ANSYS转子曲轴过盈配合有限元分析［J］.机械工程师，2010(11):119－120.

［7］张松，艾兴，刘战强.基于有限元的高速旋转主轴过盈配合研究［J］.机械科学与技术，2004(23):15－17.

［8］卢萍，崔大宾，王宁.高速列车轮轴过盈配合性能分析［J］.机械设计与制造，2010(8):196－198.

［9］徐芝纶.弹性力学简明教程［M］.北京:高等教育出版社，2006.

［10］龚曙光，等.ANSYS参数化编程与命令手册［M］.北京:机械工业出版社，2009.

［11］王新敏.ANSYS工程结构数值分析［M］.北京:人民交通出版社，2007.

(编辑 李秀敏)

Research on Interference Fit Mapping for Form Error of Axis-sleeve Parts

PAN Xu-hui
(Luoyang Institute of Electro-Optical Equipment，AVIC，Luoyang He’nan 471009，China)

Interference fits are w idely used in the connection of bearing and shaft.For precision instruments，analyzing the influence of interference fit precision caused by themachining form error is vital.ANSYS which is a sort of finite element analysis software was put into used to the axis-sleeve interference fit w ith form error for finite element simulation.And then the mapping relationship of the shaft sleeve shape error，magnitude of interference and the quantity of outer ring was analyzed.The results showed that the dimensionless deformation amplitude isminimum when themagnitude of interference and error value are constant，shaft and axis-sleeve inner diameter have the same number of error round edge;the dimensionless deformation amplitude isminimum which is close to zero when themagnitude of interference and form error are constant，shaftand axis-sleeve inner diameter have the same error value;when the error shape and error value are constant，w ith the increase of the amount of interference，the dimensionless deformation amplitude presents decreasing trend.

interference fit;form error;deformation;finite element analysis

TH122

A

1001－2265(2013)03－0012－04

2012－12－21

潘旭辉(1981—)男，河南洛阳人，中国航空工业洛阳电光设备研究所工程师，硕士主要从事光电技术相关方面的研究，(E－mail)panxuhui2012@163.com。