高中物理轻绳模型浅析

◆高 磊

(山东省济南市历城第一中学)

轻绳是中学物理中的一个理想化物理模型，绳与物块、绳与球可以组合成繁杂不一的物理情景。纵观历年高考题，有关绳模型的考查从未间断过，真可谓“无卷没有绳，无绳难成卷”。以绳模型为载体，可以对学生的知识与能力进行全方位的考查。不管是运动分析，还是受力分析，甚至是功能分析，绳模型就是一个最好的切入点。实际教学中，面对庞杂繁多、高频出现的绳模型问题，对多数学生来讲真可谓“早木皆兵，望绳色变”。

一、分清绳“绕”与“系”的问题

若绳绕过光滑的物体，如绕过光滑的滑轮、勾、环、杆等，则从始到终各段绳都是同一根绳，同一轻根绳处处弹力一定是相等的。所谓“系”的问题，即在该点“打了个死结”，这样不同段绳就不是同一根绳了，不同根绳上的弹力不一定相等，需具体问题具体分析。

例1.轻绳的两端A、B固定在天花板上，绳能承受的最大拉力为120N.现用挂钩将一重物挂在绳子上，结果挂钩停在C点，如图所示，两端与竖直方向的夹角分别为37°和53°.求:

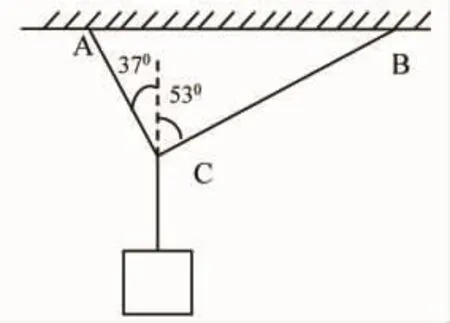
(1)此重物的最大重力不应超过多少?(sin37°=0.6，cos37°=0.8)

(2)若将挂钩换成一个光滑的小滑轮，重物的最大重力可达多大?

解析:(1)此为绳“系”模型，AC、BC为两根绳，取C点为研究对象，受力分析构建共点力模型，由几何关系可知，AC上的弹力比BC上大，则当AC上的弹力为最大值120N时，BC上的弹力小于120N，则由AC上弹力最大值120N可求得最大重力为150N.

(2)换成滑轮，则为绳“绕”模型，AC、BC为同一根绳，两段绳上的弹力大小相等，且与竖直方向夹角相等，力的矢量图为菱形，由几何关系可求得最大重力为168N.

由以分析可知对于轻绳模型，首先判定好是绳“绕”还是绳“系”的问题，确定了正确的分析方向，解决问题自然游刃有余。

二、“临界”问题

临界与极值问题是中学物理中的常见题型，临界是一个特殊的转换状态，是物理过程发生变化的转折点，在这个转折点上，系统的某些物理量达到极值。临界点的两侧，物体的受力情况、运动状态一般要发生改变。

例2.如图所示，物体A质量为m=2kg，用两根轻绳B、C连接到竖直墙上，在物体A上加一恒力F，若图中力F与水平夹角及轻绳AB与水平线夹角均为θ=60°，要使两根绳都能绷直，求恒力F的大小。

解析:要使两绳都能绷直，必须F1≥0，F2≥0，将各力正交分解由平衡条件有:

Fsinθ+F1sinθ－mg=0，Fcosθ－F2－F1cosθ=0，解得 F1=mg/sinθ－F，

F2=2Fcosθ － mgcotθ，两绳都绷直满足 F1≥0，F2≥0，

由以上解得F最大值Fmax=23.1N，解得F最小值Fmin=11.6N，

所以F的取值为11.6N≤F≤23.1N。

由以上分析可知解决临界问题，关键在于找到物体处于临界状态时的受力情况和运动情况，看临界状态时哪个力会为零，物体的加速度方向如何，然后才能正确地受力分析、运动分析，再选取相应的规律分析求之。

三、连接体问题

处理连接体问题必须灵活地应用隔离法与整体法。把所研究的对象作为一个整体来处理的方法称为整体法;把所研究的对象从整体中隔离出来进行研究，最终得出结论的方法称为隔离法。在处理实际问题时整体法和隔离法是相对统一、相辅相成的、交叉使用的。

例3.在一根绳子下面串联着两个质量不同的小球，上面小球的质量比下面小球的质量大，当手提着绳的端点O并使两球沿水平方向一起做匀加速运动时(空气阻力不计)，则图中正确的是().

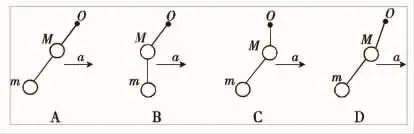
解析:设上面一段绳与竖直方向的夹角为α，下面一段绳与竖直方向的夹角为β，先对整体受力分析由牛顿第二定律有F合=(m+M)gtanα=(M+m)a，得 a=gtanα;同理对 m 有 mgtanβ =ma＇，其中 a＇=a，所以 tanβ =tanα，即α=β，故选项A正确。

例4.如图所示，一氢气球用细绳系于一个小石块上，并将小石块置于粗糙的水平地面上，若风速是水平的，且逐渐增大(设空气密度不变)，则下列描述正确的是( ).

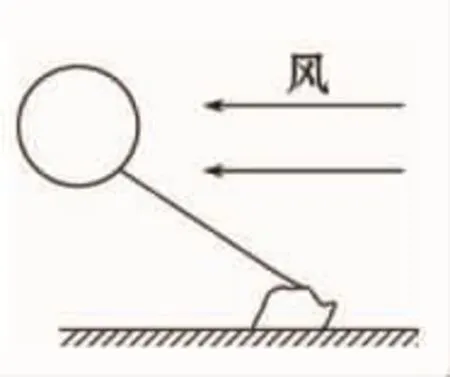
A.细绳上的弹力逐渐增大

B.地面对小石块的支持力逐渐减小

C.小石块滑动之前受到地面施加的摩擦力逐渐增大，滑动后受到的摩擦力不变

D.小石块有可能连同气球一起被吹离地面

解析:把气球和石块看做一整体，整体受到重力，地面对石块的支持力，水平风力和地面对石块的摩擦力，空气对气球的浮力和支持力的合力与重力是平衡力，石块滑动之前水平风力和地面对石块的静摩擦力是一对平衡力，滑动以后是滑动摩擦力，大小不变，故B错误，C正确;风力是水平的，在竖直方向无分力，则不管风力有多大，都不会将石块连同气球吹离地面，D错误;以气球为研究对象，易知A正确。选A、C。可见对连接体问题，依据具体问题，灵活选取研究对象，交替用好隔离法与整体法，问题自然变得柳暗花明了。

综上所述，以轻绳为纽带构建的物理模型千变万化，但它们也有共同的规律，只要把握好轻绳模型的共性，在分析具体问题时就能在宏观轻松把握住正确的方向，便可快速准确地让问题水落石出。