多相电机非正弦供电下的定子缺相容错控制

孔武斌， 黄进， 康敏， 李炳楠， 耿泽暘

(1.浙江大学电气工程学院，浙江杭州310027;2.浙江科技学院自动化与电气学院，浙江 杭州310023)

0 引言

电力机车牵引、舰船驱动、航空航天等大功率应用场合，电机驱动系统的容错运行能力尤为重要［1－4］。变频调速系统发生的故障分为电机本体故障和逆变器故障，其中由于定子绕组开路、驱动脉冲丢失或逆变器开关元件开路等原因所导致的缺相故障占很大的比例。多相电机可以提供比三相电机更多的控制自由度，增加的自由度可以用来实现在故障状态下的无扰容错运行［5－6］。

多相电机缺相后容错运行旨在故障后获得平稳的转矩输出，其主要控制思想有两种:其一，无故障情况下电机平稳运行时各d－q平面内定子电流都产生圆形旋转磁场［7－8］，缺相故障后修正剩余各相电流使它们产生的合成MMF为圆形磁场，即可获得平稳的运行性能［9－10］;其二，求解定子缺相后的转矩表达式，其含有两个分量，一个稳定值，一个脉动值，设法通过调节剩余各相电流使脉动值为零。

国内外相关文献［9－12］分别通过修正基波电流、3次谐波电流、…来保证非正弦供电下故障前后电机1、3、…次定子磁动势不变。这种方法修正后的基波电流产生的定子磁动势不变，但它忽略了修正后的基波电流还将产生3、5、7、…等次其他谐波磁动势;同理，修正后的3次谐波电流除了产生与故障前相同的3次谐波磁动势以外，还产生1、5、7等次的磁动势。本文对这种多相集中整距绕组电机在非正弦供电下的容错运行策略进行阐述，并通过比例谐振(proportional resonant，PR)算法实现相坐标系下的电流无静差控制［13］，最后进行相关实验来验证结论。

1 容错运行策略分析

集中整距绕组可以用绕组函数来表示，为方便分析表示为傅里叶级数形式，如a相绕组的绕组函数［5－6］

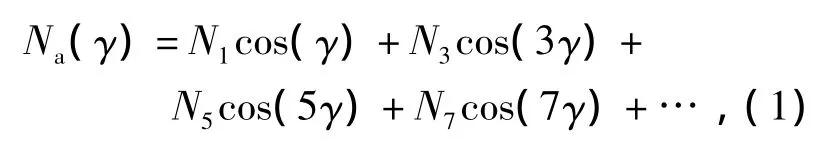
式中:γ为气隙圆周上的空间电角度，其系数Nν与ν次谐波的绕组系数 Kwν的关系为:Nν=2NφKwν/(νpπ)，Nφ为每相串联匝数;其它各相绕组的绕组函数可依此类推，相互错开2π/n电角度，n为电机相数。

以9相电机为例，对非正弦供电时的容错运行策略进行分析，保证修正后定子电流产生的定子磁动势波形与故障前相同。9相集中整距绕组电机含有4 个相互正交的平面，即 α1－ β1、α3－ β3、α5－ β5、α7－β7平面［12］，分别对应于基波和 3、5、7 次谐波。与3相电机不同，多相电机具有多个自由度，3、5、7次谐波电流产生的同次气隙磁场谐波能产生与基波同步速的旋转磁场，进而提高转矩密度和铁心利用率;当电机出现缺相故障后，也可以通过非正弦供电的容错策略保持基波和3、5、7次谐波磁场与故障前相同，抑制转矩脉动，并且获得较高的转矩密度。

以a相发生缺相故障为例分析，假设故障前各相电流分别为 ia，ib，ic，…，ii;当 a相发生故障断开后，a相电流 i'a=0，剩余各相电流变为 i'b，i'c，…，i'i。为了保持故障发生前后定子磁动势不变，取气隙圆周上任意一点γ∈［0，2π)须满足

将式(1)代入式(2)，并将 ia，ib，…，ii变换到 α－β静止坐标平面，得对于任意角度γ，下式恒成立

式中:α =2π/9，iα1、iβ1，iα3、iβ3，…分别为无故障运行时静止坐标系下的 α1－ β1，α3－ β3、…平面定子电流，由上述电流就可以推出正常运行时定子基波和3、5、…次谐波磁动势的幅值大小与相位。以α1－β1平面为例，基波磁动势的幅值大小正比于，相位取决于 iβ1/iα1。

式(3)恒成立等价于下列方程组有实根

a相发生故障时i'a=0，等价于删除上述方程组系数矩阵的第一列。该方程组前两行表示修正后的电流产生的基波磁动势与故障前相同，它具有两方面的含义:基波电流产生的磁动势与正常运行时相同;3、5、7次谐波电流产生的基波磁动势为零。

方程组(4)含有9个方程，8个未知数，即无法同时满足下面两个条件:故障前后基波和3、5、7次谐波磁动势不变;电机无中线连接。要使方程有唯一解有以下两种方法:

1)电机中线不与逆变器中点相连。由于高次谐波对电机的影响较小，可以忽略7次谐波的影响，可知此时方程组含有7个方程、8个未知数，方程组具有无穷多个解，因此需要引入其它的附加条件加以约束。

2)电机中线与逆变器中点连接。此时中线有电流通过，即各相电流之和不再被限制为零，进而使故障前后基波和 3、5、7 次磁动势保持不变［8－9］。然而，零序电流会产生9次驻波磁场，产生脉动转矩，且中线的存在也使系统复杂化。

2 附加条件约束

由前文分析可知，若忽略9相电机7次谐波的影响，需增加其它附加条件使方程组具有唯一解，如容错运行时脉动转矩最小、各相电流幅值相同、电机定子铜耗最小等。下文以定子铜耗最小为目标函数建立方程，式(4)可改写为

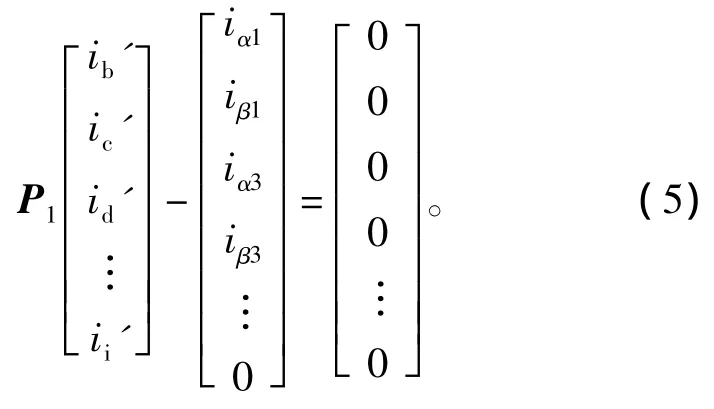
利用拉格朗日乘数法构造新函数，保持故障前后基波和3、5次定子MMF不变，定子铜耗取最小值等价于 ib'，ic'，…，ii'电流多项式取极小值。

式中:f1，f2，…，f7分别为式(5)等式左侧的各行表达式，其中 λ1，λ2，…，λ7拉格朗日系数，与电流无关。求得满足条件的最小定子铜耗所对应的极值点

写成矩阵形式为

因此，对于一定比例的各平面定子磁动势(对应于 i1α、i1β、…、i5α、i5β)，修正后的定子电流为 ib'，ic'，…，ii'。即在保持故障前后对应定子磁动势不变的条件下，这组电流解产生的定子铜耗最小。

在非正弦控制策略下，为获得优化的气隙磁动势，根据实际电机参数计算得到的注入电流比例系数为I1m∶I3m∶I5m∶I7m=1∶－0.044 2∶－0.172 4∶－0.1676，其中负号表示的是电流的相位关系［14］。由上述理论提出了非正弦供电下的3种容错控制策略:(I)忽略3、5、7次谐波后即保持故障前后基波定子磁动势不变，则此时定子铜耗为故障前的1.2倍;(II)忽略7次谐波后即保持故障前后1、3、5次定子磁动势不变，则此时定子铜耗为故障前的1.5倍;(III)通过中线连接的方式，保持故障前后基波和3、5、7次定子磁动势不变，得到定子铜耗为故障前的2倍。

根据上述方法不难求得上述3种控制策略的剩余相电流，以控制策略I为例，可以表示为

3 电流控制策略

为了实现相坐标系的电流无静差控制，采用PR控制算法［13］，如图1所示。定子给定励磁分量，转矩分量经过容错电流发生器转化为相坐标系下的电流(相电流不对称)，再将给定相电流和反馈相电流ix进行做差，然后经过PR控制器得到给定的相电压，加上反电势前馈补偿后可得到给定相电压，在频域可以表示为

其中:s为频域分析中的拉普拉斯算子，kpi为电流环比例常数，τri为电流环积分常数，ωe为谐振点角频 率为反电势为给定相电压。

图1 容错状态下的PR控制方式Fig.1 PR control strategy under fault condition

PR控制与传统的PI控制方式相比，优点在于在谐振点附近具有很高的增益，实现动态跟踪交流量，达到无静差控制效果。图2为PR控制与传统PI控制的波特图，并且采用同一组参数(kpi，τri)。

图2 PR控制和PI控制的波特图Fig.2 Bode plot of PR and PI control

4 实验结果

为了验证上述理论，构建了一套多相感应电机变频调速系统:主控芯片采用德州仪器的一款32位浮点型DSP－TMS320F28335和Altera公司的一款FPGA－EP1C6Q240C6，其中DSP用于实现复杂算法，FPGA用于扩展产生多路PWM驱动信号;采用日本YOKOGAWA公司的波形记录分析仪(型号DL750)和JN388型转矩转速传感器进行相关参数测量。

以一台9相集中整距绕组感应电机为例，实验样机参数如下:额定功率为13 kW，相电压为220 V，相电流为9 A，极对数为3，额定转速为970 r/min，额定转矩为150 N·m。

图3～图6为电机在600 r/min稳态运行时，发生单相断开故障的实验结果。图3为故障发生时无容错控制的实验结果，可以发现相电流明显增大，并且转矩有较大波动。

图3 无容错算法的实验波形Fig.3 Experimental waveforms of no fault tolerance algorithm

图4 容错算法I的实验波形Fig.4 Experimental waveforms of fault tolerance algorithm I

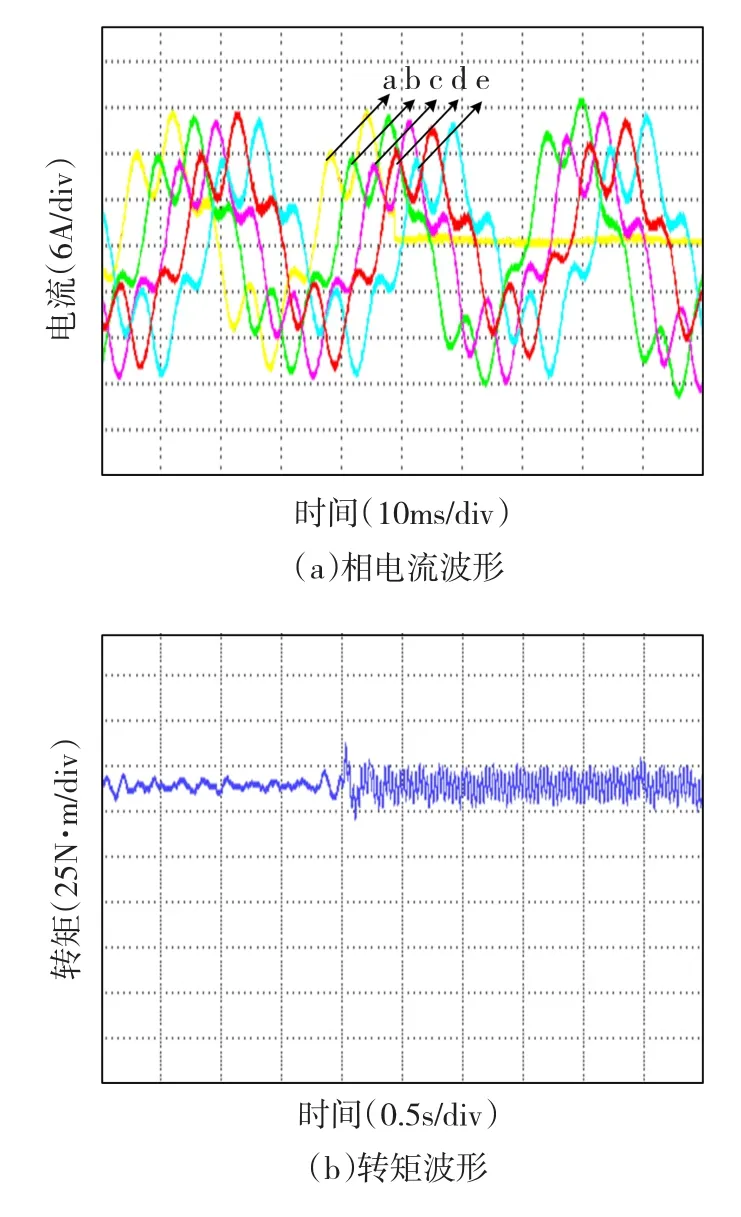
图5 容错算法II的实验波形Fig.5 Experimental waveforms of fault tolerance algorithm II

图6 容错算法III的实验波形Fig.6 Experimental waveforms of fault tolerance algorithm III

图4～图6是分别实行容错控制策略I－III的实验结果，可以发现容错控制后转矩脉动明显减小，并且随着谐波次数的增加，平均转矩也随之增大，表明非正弦供电能有效提高功率密度。由于示波器探头数限制，相电流给出了其中的5相。

表1 为3种容错控制策略的性能参数。从表中可以发现，发生缺相故障后，3种容错策略能保持转矩的稳定输出，并且转矩脉动相对较小。容错策略II，III为非正弦供电，转矩平均值有所提高，但是由于谐波电流的注入，定子铜耗也随之增大。

表1 3种容错策略的性能参数Table 1 Parameters of three fault tolerance strategies

5 结语

本文基于故障前后定子磁动势保持不变的原则，提出了9相异步电机在非正弦供电下的多种容错控制策略，并对电机损耗和转矩脉动等问题进行了相关分析。通过实验对非正弦供电下的3种容错运行策略进行比较，并对结果进行了分析，表明在非正弦供电下转矩密度得到有效提高。尽管文中仅对多相异步电机发生单相故障进行了分析，但上述理论推导对两相及两相以上发生缺相故障同样适用，进一步的研究将在以后工作中展开。

［1］LEVI E，BOJOI R，PROFUMO F，et al.Multiphase induction motor drives-a technology status review［J］.IET Electric Power Applications，2007，l(4):489－516.

［2］TOLIYAT HAMID A.Analysis of a concentrated winding induction machine for adjustable speed drive applications part I(motor analysis)［J］.IEEE Transactions on Energy Conversion，1991，16(4):679－683.

［3］杨家强，黄进，康敏，等.多相感应电机的电子变极技术［J］.电机与控制学报，2009，13(3):322 －326.YANG Jiaqiang，HUANG Jin，KANG Min，et al.Electronic pole changing technique of multi-phase induction motor［J］.Electric Mahines and Control，2009，13(3):322 －326.

［4］薛山，温旭辉，王又珑.多相永磁同步电机多维控制技术［J］.电工技术学报，2008，23(9):65 －69.XUE Shan，WEN Xuhui，WANG Youlong.Multi-dimensional control in multiphase permanent motor drives［J］.Transactions of China Electrotechnical Society，2008，23(9):65 －69.

［5］刘东，黄进，于文娟，等.空间矢量PWM多相变频调速系统非正弦供电技术［J］.电机与控制学报，2010，14(9):41－47.LIU Dong，HUANG Jin，YU Wenjuan，et al.Non-sinusoidal output voltage for multiphase variable speed drives with space vector PWM［J］.Electric Mahines and Control，2010，14(9):41 －47.

［6］黄进.p对极n相对称系统的变换理论［J］.电工技术学报，1995(1):53－57.HUANG Jin.Transformation theory for p-pair pole n-phase symmetric system ［J］.Transactions of China Electrotechnical Society，1995(1):53－57.

［7］LUO X，LIAO Y，TOLIYAT HAMID A，et al.Multiple coupled circuit modeling of induction machines［J］.IEEE Transactions on Industry Applications，1995(31):311 －318.

［8］赵品志，杨桂杰，李勇.五相永磁同步电动机单相开路故障的容错控制策略［J］.中国电机工程学报，2011，31(24):68 －76.ZHAO Pinzhi，YANG Guijie，LI Yong.Fault-tolerant control strategy for five-phase permanent magnetic synchronous motor under single phase open-circuit fault condition［J］.Proceedings of the CSEE，2011，31(24):68 －76.

［9］XU H，TOLIYAT H A，PETERSEN L J.Resilient current control of five-phase induction motor under asymmetrical fault conditions［C］//2002 Applied Power Electronics Conference and Expositio，March 10－14，2002，Dallas，USA.2002:64－71.

［10］刘东，黄进，康敏，等.多相感应电机的非正弦供电技术［J］.中国电机工程学报，2011，31(12)，84－89.LIU Dong，HUANG Jin，KANG Min，et al.Non-sinusoidal voltage fed multiphase induction motors［J］.Proceedings of the CSEE，2011，31(12):84 －89.

［11］刘东，黄进，陈高，等.FPGA在大功率多相变频调速系统中的应用［J］.电机与控制学报，2010，14(6):51－55.LIU Dong，HUANG Jin，CHEN Gao，et al.Application of FPGA in high-power multiphase variable speed drives［J］.Electric Mahines and Control，2010，14(6):51 －55.

［12］朱鹏，张晓峰，乔鸣忠，等.五相集中整距绕组感应电机缺相容错控制［J］.中国电机工程学报，2011，31(33):131 －137.ZHU Peng.ZHANG Xiaofeng，QIAO Mingzhong，et al.Tolerant control strategy for five-phase concentrated full-pitch windings induction motor under open phases fault［J］.Proceedings of the CSEE，2011，31(33):131 －137.

［13］HOLMES D G，LIPO T A，MCGRATH B P，et al.Optimized design of stationary frame three phase AC current regulators［J］.IEEE Transactions on Power Electronics，2009，24(11):2417－2426.

［14］康敏，黄进，刘东，等.多相异步电机参数的计算与测量［J］.中国电机工程学报，2010，30(24):81 －87.KANG Min，HUANG Jin，LIU Dong，et al.Calculation and measurement of parameters of a multiphase induction motor［J］.Proceedings of the CSEE，2010，30(24):81 －87.