无刷双馈电机全域多工况温度场的分析与计算

韩力， 焦晓艳， 李景灿， 王华

(重庆大学输配电装备及系统安全与新技术国家重点实验室，重庆400044)

0 引言

无刷双馈电机(brushless doubly－fed machine，BDFM)取消了电刷和滑环，提高了系统的可靠性，具有变频器容量小、系统成本低、转速和功率因数调节灵活等优点，可在单馈异步和双馈亚同步、同步和超同步等多种不同工况下稳定运行，在电动机变频调速运行以及发电机变速恒频运行方面具有良好的应用前景［1］。然而，BDFM运行机理复杂，定子功率绕组与控制绕组之间没有直接的电磁耦合，而是通过转子的磁场调制作用实现机电能量转换，磁场中谐波含量大，从而谐波铜耗和谐波铁耗大，导致BDFM的温升和发热严重。因此，准确分析并掌握BDFM的温度分布规律具有重要意义，也具有相当的难度。

为了计算电机的温升，常采用等效热路法［2］、集中参数热网络法［3］或有限元法［4－14］，针对 BDFM［3－4］、水轮发电机［5］、汽轮发电机［6－7］、感应电机［8－12］、开关磁阻电机［13］、力矩电机［14］等不同电机，进行稳态［3－11］或暂态［12－14］温度场的计算。韩力等人采用有限元法，针对不同工况、结构、材料，对大型贯流式水轮发电机转子二维暂态电磁场、三维稳态温度场进行了分析［5］;姚缨英、顾国彪等人研究了不同工况下汽轮发电机三维稳态温度场的分布，指出负荷变化对温度有一定影响［6］，而定子绝缘对温度的影响很小［7］;李伟力等人研究了感应电机定子［8］、定转子全域［9－10］二维温度场分布情况，得出不同散热翅高度［8－9］、不同负载［8，10］、不同材料［9］将影响感应电机温度的大小与分布;Bastos等人提出了采用气隙等效导热系数方法分析感应电机的温度［11］;Hatziathanassiou等人考虑集肤效应与温度对电阻的影响，对感应电机电磁场与温度场进行了耦合计算［12］;Wu Wei等人通过电磁场与温度场的有限元计算，对开关磁阻电机进行了优化设计［13］;邹继斌等人对力矩电机进行了三维暂态温度场分析，研究了定子铁心损耗与磁极表面损耗对定转子温度的影响［14］。然而，由于BDFM的结构与运行工况复杂，对BDFM温度场研究的文献还极少［3－4］，且分析的精细程度和计算的准确性还有待改进。

针对以上问题，在文献［15］的基础上，本文分析并建立了BDFM二维定转子全域温度场计算的数学模型，提出了定子铁心与机壳之间微间隙的处理方法，并详细考虑了各种材料的热属性，建立了导热系数随温度变化以及散热系数随冷却风速变化的函数关系，利用有限元法计算了BDFM的稳态和暂态温度场，分析了散热翅高度和风速变化、定子槽绝缘老化、负载转矩和控制绕组电压变化以及BDFM在变频调速过程中温度的分布与变化规律，并通过一台相似结构感应电机的温度实测数据验证了所提出模型的正确性。

1 样机模型及基本参数

以笼型转子BDFM样机为分析对象，选取定转全域为求解区域，其中包括带散热翅和接线盒的机壳、机壳与定子铁心之间的安装间隙、定子铁心和绕组、空气隙、转子铁心和绕组以及转轴等。样机的整体结构如图1所示，其基本参数见表1。

图1 笼型转子BDFM的全域结构Fig.1 The global region of BDFM with cage rotor

表1 BDFM样机的基本参数Table 1 The basic parameters of BDFM prototype

2 温度场分析的数学模型

2.1 定解问题

BDFM的冷却方式与普通感应电机相似，采用全封闭外置风扇冷却结构，机壳内部无通风系统。为了兼顾计算精度与计算速度，考虑到BDFM的实际结构与运行工况，本文假设:

1)铁心沿轴向的温度梯度为零，将三维温度场模型简化为二维温度场模型进行分析;

2)由于电磁暂态过程远短于温升暂态过程，因此忽略定转子铜耗和铁耗等热源随温度的变化;

3)定子槽内各种不同绝缘材料的热性能用等效导热系数加以分析;

4)定子铁心与机壳之间不完全贴壁，存在0.05 mm的装配间隙。

在二维直角坐标系下，设媒质各向同性，则暂态温度场的定解问题可表示为［2，12，14，16］

式中:T为待求的温度，℃;λ为导热系数，W/(m·K);q为热源密度，W/m3;c为比热，J/(kg·K);γ为密度，kg/m3;Tf为环境温度，取40℃;α 为边界线 L1、L2上的散热系数，W/(m2·K)，其中L1为机壳散热翅风沟边界、L2为机壳接线盒边界。

式(1)为求解BDFM二维暂态温度场定解问题的数学模型。当温度稳定之后，∂T/∂t=0，此时式(1)第一项的右端变为0，可得到求解二维稳态温度场定解问题的数学模型［8－10，16］。

2.2 定转子热耦合的处理

BDFM定转子之间的热耦合主要通过气隙的对流方式进行，气隙表面散热系数的准确分析对定转子全域温度场计算精度的影响很大。因此，有必要对气隙进行特殊处理。以下分别采用气隙散热系数方法、气隙等效导热系数方法进行分析。

2.2.1 气隙散热系数方法

BDFM气隙的冷却介质一方面受转子周向运动的影响，另一方面受定子内圆表面的阻滞作用。气隙的散热系数为［16］

式中:ωr为转子角速度，rad/s;nr为转子转速，r/min;D2为转子铁心外径，m。

2.2.2 气隙导热系数方法

转子旋转带动气隙的空气流动，使定子表面以及转子表面与气隙之间主要以对流方式换热，温度场与流体场耦合在一起，增加了求解难度。为简化分析，引入气隙等效导热系数的概念，用静止气体的导热系数来描述气隙中流动空气的热交换能力。经过这样处理后，可用导热方式换热的效果来等价气隙中对流方式换热的效果。

为了分析气隙中空气流动的情况，忽略齿槽效应，假设定转子表面为光滑圆柱面，则气隙雷诺数和临界雷诺数分别为［9－10］

式中:δ为气隙长度，m;υ为空气的运动粘度，m2/s，Di1为定子铁心内径，m。

当Re＜Recr时，气隙中空气的流动为层流，等效导热系数λeff等于空气的导热系数λair。当Re＞Recr时，气隙中空气的流动为紊流，气隙的等效导热系数为［8，10］:

其中:η =D2/Di1。

针对本样机的结构与转速可能的运行范围，计算表明，Re＜Recr=512。因此，气隙中空气的流动为层流，气隙的等效导热系数可直接取为空气的导热系数。而空气的导热系数计算式为［16］

式中:λair和λair0分别为t℃和0℃时标准大气压下的空气导热系数，其中λair0=0.024 42 W/(m·K)。

2.3 机壳散热系数的处理

机壳表面由散热翅和接线盒两部分组成，其表面散热系数有很大差异。由于BDFM端部外置风扇的作用，机壳表面散热翅风沟内的空气具有较大的流速，为强制对流换热，辐射散热的影响可以忽略，其表面散热系数为［16］

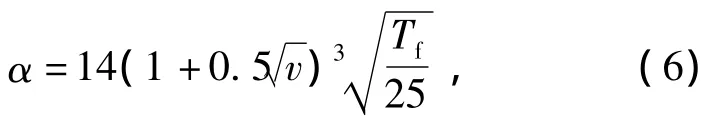
式中:v为吹拂散热翅风沟的风速，m/s。

由于接线盒的存在，在机壳表面接线盒区域的风速接近为零［9－10］，自然对流散热和辐射散热起主要作用。借鉴文献［8－9］的思想，根据式(6)在得到自然对流散热系数的基础上，再乘以1.1的修正系数来表征对流和辐射的综合作用效果。这样，可求出接线盒区域的散热系数为19.48 W/(m2·K)。

2.4 定子槽绝缘导热系数的处理

样机功率绕组采用双层叠绕组，置于定子槽下部;控制绕组采用单层同心式绕组，置于定子槽上部。在每个定子槽中，有3个线圈边(参见图6)，每个线圈由散下线绕制而成。设槽绝缘(包括槽底绝缘和层间绝缘的等效)厚度为d1，槽绝缘与定子铁心之间的空气间隙为d2，散下导线漆膜厚度为d3，散下导线之间的等效空气间隙为d4。为了简化计算，定子槽内各种绝缘材料的等效导热系数可表示为［12］

式中:λ1为槽底绝缘和层间绝缘的等效导热系数，W/(m·K);λ3为导线漆膜的导热系数，W/(m·K)。

2.5 定子铁心与机壳装配间隙的处理

考虑到定子铁心与机壳之间并非完全贴壁，而有一层δ1=0.05 mm的装配间隙。为了便于有限元单元剖分，对装配间隙进行等效处理。在机壳侧取δ2=1 mm厚的薄层，与厚度为δ1的装配间隙合并，然后对δ1+δ2厚度范围内的等效机壳进行有限元单元剖分，如图2所示。

图2 等效机壳Fig.2 The equivalent stator frame

通过以上处理，机壳等效导热系数可表示为

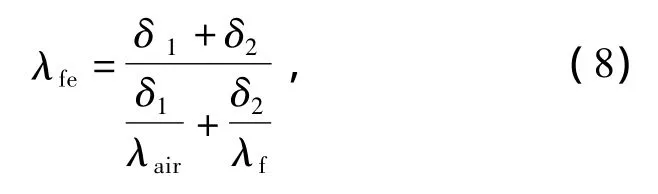
式中:λf为机壳的导热系数，W/(m·K)。

2.6 其他材料的热属性

导热系数的大小与材料的性质有关，同一材料的导热系数随温度、压力、湿度、多孔性和均匀性等因素而变化，通常温度是决定性因素。对绝大多数材料而言，当温度尚未达到熔化或汽化以前，导热系数可近似认为随温度呈线性规律变化［16］

式中:λ0为材料在0℃时的导热系数，W/(m·K);b为由实验确定的材料常数，可为正值也可能为负值，℃－1;t为实际温度，℃。

样机采用B级绝缘，查阅相关技术资料［16－17］，可得到BDFM其他各部件在0℃时的导热系数λ0以及材料常数b。与此同时，给出定解问题式(1)中所需用到材料的比热c和密度γ，如表2所示。

由此，经过上述较为述详细的分析，建立了BDFM定转子全域温度场计算的数学模型。以下将根据表1的样机数据和表2的材料热属性，利用ANSYS WORKBENCH 13.0软件，采用有限元法，对图1所示的笼型转子BDFM定转子全域温度场进行具体计算。

表2 笼型转子BDFM各部件的热属性Table 2 The heat characteristics of different parts of BDFM with cage rotor

3 稳态和暂态温度场计算实例

在下文中，如不加特别说明，样机的运行条件设定为:功率绕组电压和频率保持额定值不变，控制绕组与功率绕组电流同相序，控制绕组频率fc=13 Hz，控制绕组相电压Uc=130 V，散热翅风沟的风速v=3.7 m/s，BDFM处于超同步恒速空载稳定运行工况。

在考虑谐波磁场、谐波电流、转子集肤效应以及铁心交变磁化和旋转磁化的影响下，根据文献［15］提出的BDFM谐波铜耗和谐波铁耗计算模型，首先计算得到在不同负载转矩TL下样机定转子的铜耗和铁耗，从而得到各部分的热源密度，如表3所示。其中，qCup、qCuc、qCur、qFes、qFer分别为定子功率绕组、定子控制绕组、转子绕组、定子铁心、转子铁心的热源密度，其大小均为表中数据×10－6W/mm3。

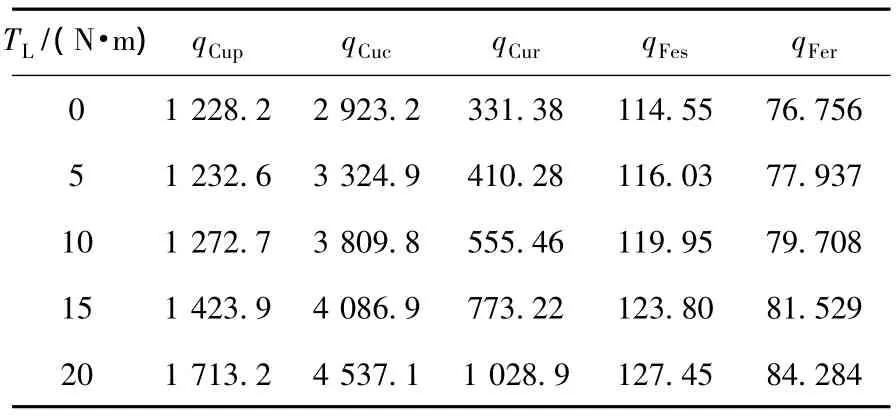
表3 BDFM在不同负载下的热源密度Table 3 Heat source density of BDFM under different loads

由表3可见，随着负载转矩的增大，热源密度逐渐增加，这必将导致BDFM温度的升高。同时可见，在同一负载转矩下，定子控制绕组的热源密度最大，而定子槽绝缘的导热系数较低，因此可以测定子控制绕组及槽内绝缘的温度较高。

3.1 稳态温度场计算

根据稳态温度场模型，分别采用气隙散热系数方法和气隙等效导热系数方法，通过有限元计算得到样机定转子全域稳态温度场的分布，如图3所示。

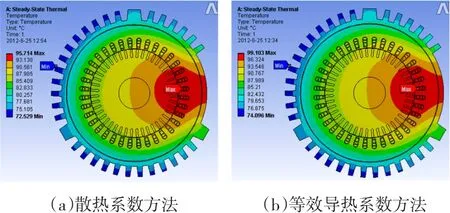
图3 BDFM稳态温度分布Fig.3 Steady state temperature distribution of BDFM

由图3可见，两种不同方法得到的全域温度分布规律相同，最高温度和最低温度分别位于接线盒附近的定子控制绕组上部以及接线盒对面的机壳散热翅顶部;最高温度和最低温度的数值也分别十分接近，两种不同方法得到的最高温度分别为95.7℃和99.1℃(相差3.5%)、最低温度分别为72.5℃和74.1℃(相差2.2%)，从而佐证了两种不同计算方法的正确性。此外，由于接线盒处为自然对流换热，散热系数小，而散热翅风沟为强制对流换热，散热系数大，散热效果好，从而导致BDFM温度分布不均匀。

由于以上两种不同方法的计算偏差很小，为了简化讨论，以下统一采用气隙等效导热系数方法来处理气隙的热交换能力。

3.2 暂态温度场计算

根据暂态温度场模型，采用有限元法进行计算，在不同时刻得到的样机定转子全域温度场分布规律如图4所示。由此可见，样机在运行初始阶段，定转子全域中温差不大，各部分温度分布比较均匀，最高温度和最低温度分别为47.1℃和43.1℃;当样机运行到100 min时，定转子全域中温差明显增大，位于接线盒附近的定子控制绕组温度最高，达到98℃，而位于接线盒对面的机壳散热翅温度最低，仅有73.7℃。

图4 BDFM暂态温度分布Fig.4 Transient temperature distribution of BDFM

图5给出了样机定转子全域中最高温度Tmax(即控制绕组温度)随时间的变化规律。由此可见，随着运行时间的增加，最高温度按指数规律增加，在120 min之后，最高温度基本不再变化，最后稳定于98℃，该数据与稳态温度场计算得到的最高温度99.1℃十分接近。为了提高计算效率、缩短计算时间，在下面第4节“结构与运行工况对最高温度的影响”分析中，将统一采用稳态温度场模型进行计算。

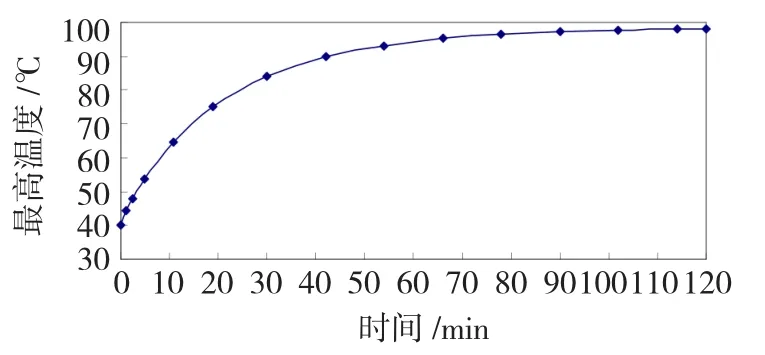
图5 不同时刻的最高温度Fig.5 Maximum temperature at different time

为了进一步分析样机不同位置温度随时间的变化规律，选取接线盒侧区域与背离接线盒侧区域，其中图6(a)对应于图1中的X区域，图6(b)对应于图1中的Y区域。用大写字母A、B、C、D、E、F和小写字母 a、b、c、d、e、f分别表示 X 区域和 Y 区域内定子槽口绝缘、定子功率绕组、定子控制绕组、转子导条、定子铁心、转子铁心处的典型位置。

图6 BDFM各部分温度计算点Fig.6 Different points for BDFM temperature calculation

对以上各点在不同时刻的温度分布情况进行有限元计算，其结果如图7所示。由此可见，X区域的温度明显高于Y区域的温度;在X区域，各部件温度的大小与变化规律基本相同;而在Y区域，各部件的温度出现差异，其中转子铁心温度高于其它部件，其原因是Y区域内的转子铁心远离散热翅。

4 结构与运行工况对最高温度的影响

为了进一步研究结构与运行工况对温度的影响，探讨不同情况下BDFM定转子全域最高温度的分布规律，下面分别针对散热翅高度、散热翅风速、槽绝缘老化、负载转矩、控制绕组电压、变频调速运行工况等发生变化的情况，进行定转子全域稳态温度场计算，并对计算结果进行分析。

图7 BDFM各部分的暂态温度分布Fig.7 Transient temperature distribution of different points

4.1 散热翅高度变化

在样机的原始设计方案中，散热翅高度为20 mm。为了研究散热翅高度对最高温度的影响，保持其它条件不变，单独考虑散热翅高度从10 mm变化到40 mm，计算结果如图8所示。由此可见，随着散热翅高度的增加，样机的最高温度从115.1℃降低到85.9℃，减小了25%。但随着散热翅高度的增加，温度曲线的斜率逐渐下降，降温效果出现“饱和现象”。由此可知，应合理设计散热翅的高度。

图8 散热翅高度对最高温度的影响Fig.8 The influence of fin height on Tmax

4.2 散热翅风速变化

保持其它条件不变，单独考虑散热翅风沟风速v的变化，计算结果如图9所示。由此可见，最高温度随v的增加而降低。当v=1 m/s时，最高温度为146.2℃;当v=10 m/s时，最高温度降到76.7℃。但当v＞4 m/s后，降温效果也出现了“饱和现象”。因此，应合理选配外置风扇，既要注意保证BDFM的温升不超标，也要注意降低通风损耗。

图9 散热翅风沟风速对最高温度的影响Fig.9 The influence of fin duct wind speed on Tmax

4.3 定子槽绝缘老化

保持其他条件不变，单独考虑定子槽绝缘由于老化的影响，其导热系数从0.16 W/(m·K)降低到0.1 W/(m·K)，模拟定子槽绝缘的老化过程，计算结果如图10所示。由此可见，随着定子槽绝缘的老化，其导热系数降低，样机最高温度略有增加，几乎呈线性变化。当定子槽绝缘的导热系数为0.16 W/(m·K)时，最高温度为99.1℃;当定子槽绝缘因老化而导热系数降低到0.1 W/(m·K)时，最高温度变为99.3℃，最高温度仅升高了0.2℃。由此可见，在一定程度内，定子槽绝缘的老化对最高温度影响不大，可忽略不计。

图10 定子槽绝缘老化对最高温度的影响Fig.10 The influence of stator slot insulation ageing on Tmax

4.4 负载转矩变化

保持其他条件不变，让负载转矩从0变化到20 N·m，计算结果如图11所示。由此可见，最高温度随着负载转矩的增加而明显增大，其原因是定转子电流和铜耗增大［15］，导致温度升高。当负载转矩为0时，最高温度为99.1℃;当负载转矩为20 N·m时，最高温度变为129.4℃，升高了30.3℃，变化了30.6%。

图11 负载转矩对最高温度的影响Fig.11 The influence of load torque on Tmax

4.5 控制绕组电压变化

保持其他条件不变，调节控制绕组电压Uc，计算结果如图12所示。由此可见，随着Uc的升高，最高温度逐渐增加，当Uc超过130 V时，曲线的斜率增大，最高温度升高加快。当Uc从100 V增大到150 V时，最高温度从94℃增加到124℃，升高了30℃，变化了31.9%。这是由于随着控制绕组电压的升高，BDFM的谐波铜耗和谐波铁耗增加［15］，从而导致发热增加、温度升高。

图12 控制绕组电压对最高温度的影响Fig.12 The influence of control winding voltage on Tmax

4.6 变频调速运行

改变控制绕组电流的频率fc，BDFM可在单馈异步以及双馈亚同步、同步和超同步等多种不同方式下稳定运行，实现变频调速。其转速表达式为［1，3］

当控制绕组开路时，为单馈异步运行工况;当控制绕组与功率绕组电流相序相反时，式(10)中fc前取负号，为双馈亚同步运行工况;当控制绕组采用两并一串的方式通入直流电时，fc=0，为双馈同步运行工况;当控制绕组与功率绕组电流相序相同时，式(10)中fc前取正号，为双馈超同步运行工况。

为了研究变频调速过程中最高温度的变化情况，设样机空载运行，在双馈亚同步与超同步工况时，控制绕组采用Uc/fc=10的恒压频比控制策略，在双馈同步工况时，控制绕组施加40 V的直流电。在转速变化过程中，设散热翅风沟的风速随转速按正比变化，而其他条件保持不变。计算结果见表4。

表4 不同运行工况对最高温度的影响Table 4 The influence of different operating states on Tmax

由表4可见，BDFM在单馈异步和双馈同步空载运行时，最高温度很低;而控制绕组采用恒压频比控制策略后，最高温度明显升高;控制绕组频率值越大，BDFM的转速越偏离同步运行点，最高温度也越大;在控制绕组频率值相同时，双馈亚同步运行时的最高温度大于双馈超同步运行时的最高温度。其原因是，BDFM在双馈亚同步运行时的损耗更大，且由于转速减低，致使散热翅风沟的风速减小，冷却效果降低。

5 实验验证

由于缺乏BDFM样机的温升实验数据，为了验证上述温度场模型与计算结果的正确性，本文选定一台与BDFM样机的额定容量、额定转速、主要尺寸以及定转子槽数均接近的Y2－160M2－8感应电机进行对比，该电机的基本参数如表5所示，其各件材料的热属性与表2相同。

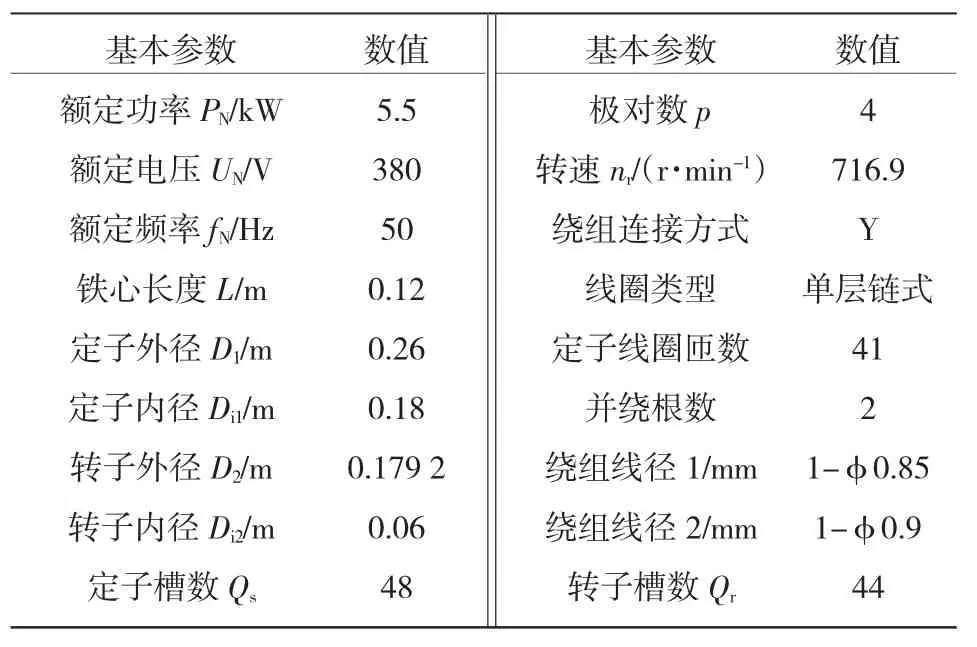
表5 Y2-160M2-8基本参数Table 5 The basic parameters of Y2-160M2-8

在环境温度为40℃时，采用电阻法进行实验，测得Y2－160M2－8感应电机在额定运行时的定子绕组平均温度为93.8℃，采用热球式风速仪测得散热翅风沟的平均风速v=3 m/s。在文献［15］基础上，考虑到定子铁心与机壳之间有0.05 mm的装配间隙，采用本文的模型对同一台感应电机在额定运行时的稳态温度场进行有限元计算，得到的定子绕组最高温度为95.5℃、最低温度为86.5℃。因此，定子绕组的平均计算温度为91℃，与实测温度93.8℃相差2.8℃，计算误差为3%，从而间接验证了本文模型与计算结果的正确性。

6 结论

本文提出了较为详细的BDFM全域多工况二维温度场分析模型，通过稳态与暂态温度场的有限元计算以及相似结构感应电机温度实测数据的验证，验证了提出模型的正确性，并得到如下结论:

1)BDFM的谐波含量及其引起的损耗和发热大，全域中温度分布不均，最高温度位于接线盒附近的定子控制绕组上部;

2)增加散热翅高度、提高散热翅风速、减小负载转矩、降低控制绕组电压，可明显降低BDFM的温升，而定子槽绝缘在一定程度内老化对温升几乎没有影响;

3)运行工况对BDFM的温升有显著影响，在单馈异步或双馈同步运行时，BDFM的最高温度较低;而采用控制绕组恒压频比控制策略后，在双馈亚同步或双馈超同步运行时，BDFM的最高温度明显增加，且双馈亚同步运行时的温升高于双馈超同步运行时的温升。

致谢

感谢中国煤炭科工集团重庆研究院防爆电器研究所马南平总工提供的Y2－160M2－8感应电机温度实验数据。

［1］MCMAHON R A，ROBERTS P C，WANG X，et al.Performance of BDFM as generator and motor［J］.IEE Proceedings － Electric Power Applications，2006，153(2):289 －299.

［2］李德基，白亚民，曹国宣.发电机暂态三维温度场的计算［J］.中国电机工程学报，1989，5(9):56－63.LI Deji，BAI Yamin，CAO Guoxuan.The transient three-dimensional temperature field calculation in generators［J］.Proceedings of the CSEE，1989，5(9):56－63.

［3］MATHEKGA M E，MCMAHON R A，SHAO S，et al.Study of the electric loading aspects of the BDFM using a lumped parameter thermal model［C］//5th IET International Conference on Power E-lectronics，Machines and Drives，April 19 －21，2010，Brighton，UK.2010:1－6.

［4］赵铮，刘慧娟，张千.径向叠片磁阻转子无刷双馈电机的电磁场及温度场分析［J］.微电机，2011，44(3):13－16.ZHAO Zheng，LIU Huijuan，ZHANG Qian.Analysis of electromagnetic and temperature field of novel brushless doubly fed machine with radial laminated reluctance rotor［J］.Micro Motors，2011，44(3):13－16.

［5］范镇南，韩力，周光厚，等.大型贯流式水轮发电机阻尼绕组损耗与发热［J］.高电压技术，2011，37(2):468－475.FAN Zhennan，HAN Li，ZHOU Guanghou，et al.Losses and heat on damper winding in large tubular hydro－ generator［J］.High Voltage Engineering，2011，37(2):468－475.

［6］夏海霞，姚缨英，熊素铭，等.1000MW汽轮发电机端部磁－热耦合分析［J］.中国电机工程学报，2008，28(14):118－122.XIA Haixia，YAO Yingying，XIONG Suming，et al.Magneticthermal coupling analysis of end region of 1000 MW turbine-generator［J］.Proceedings of the CSEE，2008，28(14):118 －122.

［7］栾茹，傅德平，顾国彪.135MW蒸发冷却汽轮发电机定子绝缘结构的研究［J］.电工电能新技术，2006，25(2):24－28.LUAN Ru，FU Deping，GU Guobiao.Research on stator insulation structure of 135MW evaporative cooling turbo-generator［J］.Advanced Technology of Electrical Engineering and Energy，2006，25(2):24－28.

［8］靳延船，李伟力，李守法.感应电机定子温度场的数值计算［J］.电机与控制学报，2006，10(5):492－497.JIN Yanchuan，LI Weili，LI Shoufa.Numerical calculation and analysis of stator thermal field in an induction machine［J］.Electric Machines and Control，2006，10(5):492 －497.

［9］李伟力，李守法，谢颖，等.感应电动机定转子全域温度场数值计算及相关因素敏感性分析［J］.中国电机工程学报，2004，27(24):85－91.LI Weili，LI Shoufa，XIE Ying，et al.Stator-rotor coupled thermal field numerical calculation of induction motors and correlated factors sensitivity analysis［J］.Proceedings of the CSEE，2004，27(24):85－91.

［10］曹君慈，李伟力，程树康，等.复合笼条转子感应电动机温度场计算及相关性分析［J］.中国电机工程学报，2008，28(30):96－103.CAO Junci，LI Weili，CHENG Shukang，et al.Temperature field calculation and associated factor analysis of induction motor with compound cage rotor［J］.Proceedings of the CESS，2008，28(30):96－103.

［11］BASTOS J P，CABREIRA M F R R，SADOWSKI N，et al.A thermal analysis of induction motors using a weak coupled modeling［J］.IEEE Transactions on Magnetics，1997，33(2):1714 －1717.

［12］HATZIATHANASSIOU V，XYPTERAS J，ARCHONTOULAKIS G，et al.Electrical-thermal coupled calculation of an asynchronous machine［J］.Archiv für Elektrotechnik，1994，77:117－122.

［13］WU Wei，DUNLOP J B，COLLOCOTT S J，et al.Design optimization of a switched reluctance motor by electromagnetic and thermal finite-element analysis［J］.IEEE Transactions on Magnetics，2003，39(5):3334 －3336.

［14］邹继斌，张洪亮，江善林，等.电磁稳态条件下的力矩电机三维暂态温度场分析［J］.中国电机工程学报，2007，27(21):66－70.ZHOU Jibin，ZHANG Hongliang，JIANG Shanlin，et al.Analysis of 3D transient temperature field for torque motor in the state of steady electromagnetic field［J］.Proceedings of the CSEE，2007，27(21):66－70.

［15］韩力，王华，马南平，等.无刷双馈电机谐波铜耗与铁耗的分析与计算［J］.电机与控制学报，2012，16(3):22－29.HAN Li，WANG Hua，MA Nanping，et al.Calculation and analysis of harmonic copper losses and iron losses of brushless doubly-fed machine［J］.Electric Machines and Control，2012，16(3):22－29.

［16］魏永田，孟大伟，温嘉斌.电机内热交换［M］.北京:机械工业出版社，1998:251 －278.

［17］马庆芳，方荣生，项立成，等.实用热物理性质手册［M］.北京:中国农业机械出版社，1986:650－667.