一种LCL滤波器有源阻尼策略与设计方法
刘计龙, 马伟明, 肖飞, 陈明亮, 杨旭
(1.西安交通大学电气工程学院,陕西西安710049;2.海军工程大学电气工程学院,湖北武汉430033)
0 引言
三相电压型PWM(pulse width modulation)变换器在新能源接入电网装备中被广泛采用,其具有功率因数可调节和入网电流谐波畸变率小等优点。三相桥变换器的输出电压含有开关频率次谐波,不能直接并网,在变换器和电网之间需要有滤波器滤除开关频率次谐波[1-3]。
传统的滤波器采用单电感滤波器,由于大功率PWM变换器的开关频率较低,需要较大的滤波电感才能满足入网电流的总畸变率指标。较大的滤波电感大大增加了系统的重量、体积与成本,而且降低了电流环的响应速度[4]。和单电感滤波器相比,LCL滤波器具有较强的高频谐波抑制能力,使用的磁性材料总量较小,降低了变换器的体积与成本[5]。
LCL滤波器对于高频谐波电流表现出很大阻抗,因此具有较强的高频谐波抑制能力。但LCL滤波器对于某些特定频次的谐波表现的阻抗很小,接近于零,使LCL滤波器的增益特性在这些特性频次上有一个谐振峰,这些特定频次的谐波电流不但不会被抑制,反而会被LCL滤波器放大。因此,这个谐振峰会导致PWM变换器不稳定[4-8]。
为了抑制LCL滤波器的谐振峰,提高系统的稳定性,需要采取措施增加LCL滤波器在谐振频率处的阻尼。增加系统阻尼的方法分为2种:无源阻尼法和有源阻尼法[4,8-11]。无源阻尼法中最常有且有效的方法是在LCL滤波器的电容支路串联阻尼电阻,引入的无源阻尼电阻增加了LCL滤波器在谐振频率处的阻尼,削弱了LCL滤波器的谐振峰。同时,无源阻尼电阻会带来额外的阻尼损耗,引起变换器的发热问题,需要辅以强制风冷或水冷等冷却措施。有源阻尼法是通过控制算法来增加系统的阻尼,抑制系统的谐振峰。有源阻尼法没有阻尼损耗问题,但增加了控制算法的复杂度[11]。
已经有很多文献对无源阻尼法和有源阻尼法进行了研究[8-11],对2种方法进行对比研究以提出有源阻尼控制策略参数设计原则的文献较少。本文对电容支路电流反馈有源阻尼控制策略和无源阻尼策略的性能进行了对比研究,从传递函数和波特图上对2者进行了对比分析,提出了电容支路电流反馈有源阻尼控制策略的参数设计原则以实现和无源阻尼法相同的性能。通过仿真验证,本文提出的参数设计原则能实现较好的控制性能,输出电流谐波降低,电流控制环的带宽可以进一步提高,变流器的动态性能得到改善。
文献[12]中采用电容电压反馈进行有源阻尼控制,在电容电压反馈通道上采用超前-滞后环节。超前滞后环节的幅频特性类似于高通滤波器,具有选频特性和高通特性,系统低频段的增益会下降且抗高频干扰的能力较弱。选用电容电流作为有源阻尼控制的反馈量时,反馈通道上只需采用比例环节,系统低频段和高频段增益不受影响。
电容支路电流反馈有源阻尼法是采用陷波器来矫正LCL滤波器的谐振峰,从系统结构上讲,该方法实际上是在控制系统中构造一个具有负谐振峰的环节,并以此抵消LCL滤波器产生的正谐振峰[4]。从实际的物理意义上讲,该方法实际上是对谐振频率处电流成分的负反馈,从而抑制谐振频率处的电流成分。
本文所提有源阻尼控制策略需要增加一组电流传感器测量电容支路电流或者进行电容支路电流的在线估计。增加的一组电流传感器增加了系统成本,因此这种有源阻尼控制策略更适合于中大功率的大型变流器。
1 LCL滤波器的数学模型
对LCL滤波器的谐振峰特性和稳定性分析是基于滤波器的精确数学模型。在电压型并网逆变器中,对网侧电流的控制是通过对逆变器桥臂侧输出电压的控制来实现的[4],本节重点分析滤波器的输入电压对输出电流的传递特性。
图1是单相的LCL滤波器的模型,三相LCL滤波器特性的与单相LCL滤波器的特性是一致的,对单相LCL滤波器特性的讨论分析,不失其一般性。在图1中Rf和Rg分别是逆变器侧电感Lf和网侧电感Lg的串联等效寄生电阻;Rd代表电容C的串联等效电阻和串联在电容支路的无源阻尼电阻;vi为逆变器桥臂侧输出电压;vg为电网电压。

图1 并网型LCL滤波器的模型Fig.1 Model of the LCL filter connected with the grid
根据图1给出的LCL滤波器的模型画出LCL滤波器的结构框图如图2所示,根据此结构框图可以得到LCL滤波器的如下传递特性:桥臂侧输出电压到入网电流的传递特性;桥臂侧输出电压到桥臂侧电流的传递特性;桥臂侧输出电压到电容支路电流的传递特性。其传递特性分别如式(1)、式(2)、式(3)所示。根据式(1)画出的LCL滤波器的波特图如图3所示,这里的阻尼电阻Rd只考虑电容的串联等效电阻。同时,图3也给出了使用了同等电感材料L滤波器的波特图。

图2 LCL滤波器的结构框图Fig.2 Structure diagram of LCL filter
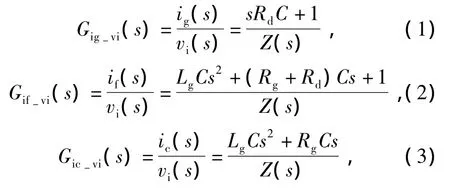
其中


图3 LCL滤波器和等电感的L滤波器的波特图Fig.3 Bode diagram of LCL filter and L filter with the equal inductance
通过图3可以看出LCL滤波器的增益特性在谐振频率处有一个峰值,即LCL滤波器对谐振频率处的电流谐波阻抗很小;LCL滤波器的相角特性在谐振频率处从-90°骤然下降到-270°;LCL滤波器在高频段的增益要远低于同等电感材料的L滤波器。
2 无源阻尼法的性能
电感的串联等效电阻对谐振峰的影响很小,当网侧电感的串联等效电阻达到电感电抗的10倍以上时,才会显著抑制谐振峰[4]。而电感的实际串联等效电阻很小,为了简化分析,忽略电感的串联等效电阻的影响。
变换器采用网侧电流反馈进行控制,重写LCL滤波器的桥臂侧输出电压到入网电流的传递特性为

已有文献提出了无源阻尼电阻的设计方法,阻尼电阻约为电容在谐振频率处容抗的1/3。基于1 MW并网逆变器,画出添加阻尼电阻后的LCL滤波器的系统波特图如图4所示。电容在谐振频率处的容抗为0.303 Ω,选择的阻尼电阻为0.1 Ω。

图4 阻尼电阻对滤波器性能的影响Fig.4 Influence of the damp resistor on bode plot of the LCL filter
图4表明阻尼电阻对滤波器性能的影响,可以得出,一个较小的阻尼电阻能够显著抑制LCL滤波器的谐振峰,并且对高频处的增益影响不大,这充分说明了无源阻尼法的良好性能。但是,无源阻尼法带来的阻尼损耗问题不容忽视,尤其是在中大功率变流器中。以1 MW并网逆变器为例,阻尼电阻的损耗约为1 000~1 500 W,损耗所引起的发热问题是严重的。
3 有源阻尼法及与无源阻尼法的对比
为了避免无源阻尼的发热问题,有不少文献研究了有源阻尼控制策略[4,8,11]。有源阻尼法可以分为3类:虚拟电阻法、陷波器校正法和双带通滤波器法[4]。本文所提出的电容电流反馈有源阻尼法实质上是一种陷波器校正法。
本文提出的LCL滤波器电容电流反馈有源阻尼控制策略的结构框图如图5所示。采用该有源阻尼控制策略时逆变器输出电压到并网电流的传递函数特性如式(5)所示。


图5 有源阻尼法控制结构框图Fig.5 Structure diagram of the active damping method
对比式(4)与式(5)可以发现,只要电容电流反馈系数x取值合适,式(4)和式(5)的分母是可以完全相同的,只要电容电流反馈系数x取值如式(6)所示。两式的分子也不同,采用无源阻尼法时传递特性的分子上是一个比例微分项,采用有源阻尼法时传递特性的分子上是一个比例项。这直接导致了有源阻尼法的传递特性在高频段的增益和比无源阻尼法更低,这说明有源阻尼法对高频噪声的抑制能力没有受到影响。和无源阻尼法相比,这是有源阻尼法的优点之一。
图6给出了有源阻尼法的无源阻尼法的传递特性波特图,从图中得出,2种方法在低频段和谐振频率附近增益是相同的。而在高频段有源阻尼法的增益较低,对高频噪声抑制能力更好。有源阻尼法高频段的增益低带来的另一个问题是有源阻尼法的相位跌落较大,比无源阻尼法多90°的相位跌落。因此,该有源阻尼法虽然相对于无阻尼方式提高了稳定裕量,但其稳定裕量相对于无源阻尼法有所降低。

图6 有源阻尼法和无源阻尼法的对比Fig.6 The active and reactive damping methods
通过添加合适的PI调节器后,系统的截止频率实际位于谐振频率的左侧,即远小于谐振频率,因此,采用该有源阻尼法对相角稳定裕量的影响并不大。该有源阻尼法抑制了系统的谐振峰,相对于无阻尼方式,使添加PI调节器后的系统带宽得到提高,并抑制了谐振频率处的电流谐波。
通过图7可以看出没有增加阻尼的LCL滤波器与采用有源阻尼法的LCL滤波器只有在谐振频率处有差异,在低频段和高频段的增益都是相同的。LCL滤波器的谐振峰被抑制,同时不降低LCL滤波器对高频噪声的抑制能力。但是无源阻尼法对LCL滤波器在开关频率处增益的影响很小,从图4或图6中可以看出只有2 dB左右,所以,有源阻尼法在这方面的优势其实很小。同时,有源阻尼法的电容电流反馈依靠对电容电流的采样和离散控制器实现,这和实际的阻尼电阻有很大的区别,这一点会影响电容电流反馈有源阻尼法的性能。

图7 LCL滤波器和有源阻尼法的传递特性波特图Fig.7 Bode plot of LCL filter and LCL filter with active damping method
考虑到系统的低控制带宽和数字控制的延迟对有源阻尼法的影响,对于大功率变流器,可以在不改变开关频率的前提下,提高执行PI控制的频率,使执行PI控制的频率是开关频率的整数倍,降低控制延迟对有源阻尼法的影响。开关频率为3 kHz,选定执行PI控制的频率为开关频率的5倍,则该延迟环节如式(7)所示,式中的Ts为执行PI控制的周期,为系统数字控制延迟的最大值。将该延迟环节添加到电容电流的反馈通道上,得到考虑系统延迟的系统传递函数,如式(8)所示。

图8是考虑系统控制延迟后有源阻尼法前后对比曲线。由图8可以看出,考虑系统控制延迟后,有源阻尼法对系统谐振峰的抑制能力有所降低,这是有源阻尼法和无源阻尼法的重要区别之一,这也是有源阻尼方法不足的地方。由图8及后面章节的仿真结果可以看出,这一影响并不大。

图8 考虑系统控制延迟后有源阻尼法前后对比Fig.8 The active damping method considering the system control delay
4 仿真结果
基于1 MW并网逆变器在SIMULINK中对无源阻尼策略和有源阻尼控制策略进行了仿真,如图9~图14所示。图9和图10分别是无阻尼方式仿真得到的三相电压电流波形图和电流频谱图。图11和图12分别是对无源阻尼法进行仿真得到的三相电压电流波形图和电流频谱图。图13和图14分别是对有源阻尼法进行仿真得到的三相电压电流波形图和电流频谱图。图10、图12、图14对应的基波频率为50 Hz。

图9 无阻尼方式仿真电压和电流波形Fig.9 Voltage and current waveforms got by simulation without damping method

图10 无阻尼方式仿真电流频谱Fig.10 Current spectrum got by simulation without damping method

图11 无源阻尼法仿真电压和电流波形Fig.11 Voltage and current waveforms got by simulation with reactive damping method

图12 无源阻尼法仿真电流频谱Fig.12 Current spectrum got by simulation with reactive damping method

图13 有源阻尼法仿真电压和电流波形Fig.13 Voltage and current waveforms got by simulation with active damping method

图14 有源阻尼法仿真电流频谱Fig.14 Current spectrum got by simulation with active damping method
由于电流环采用网侧电流反馈控制,变换器的功率因数较高,输出电流的总谐波畸变率较小,变换器具有更好的动态性能。图10的电流频谱中,谐波分布在谐振频率处和开关频率处,和图12相比较,图10谐振频率处的谐波没有得到抑制。从图12电流频谱中看出,谐波主要分布在开关频率处,谐振频率附近的谐波得到一定程度的抑制。
通过对图13和图11进行对比、图14和图12进行对比,电容电流反馈有源阻尼控制策略取得了和无源阻尼法相似的效果,2种方法对应的输出电流频谱是一致的。采用有源阻尼法时,谐振频率处的谐波比无源阻尼法略高,总谐波畸变率也略高。这是由于系统控制延迟对有源阻尼法性能有一定的影响。然而这一影响较小,可以认为该有源阻尼法取得了和无源阻尼法等效的性能。
5 结语
本文旨在分析电容电流反馈有源阻尼控制策略并将其与无源阻尼策略进行对比研究。分析了LCL滤波器的输入电压到输出电流的传递特性,从系统的波特图上可以清晰看到导致LCL滤波器系统不稳定的原因,即LCL滤波器的谐振峰特性。在LCL滤波器的电容支路添加一个小的阻尼电阻会显著改善LCL滤波器的谐振峰特性,LCL滤波器在谐振频率处的谐振峰被抑制的同时,其在高频段的增益有所提高,降低了其对高频噪声的抑制能力。分析了添加电容电流反馈后LCL滤波器系统的传递特性有哪些改变,得出电容电流反馈系数决定了有源阻尼控制策略的性能,通过选择合适的反馈系数能够使有源阻尼法取得和无源阻尼法等效的滤波性能。通过对2种方法的对比得出,电容电流的反馈系数与期望的阻尼电阻、变换器侧电感和网侧电感有关系。通过对系统进行仿真,文章最后给出采用无源阻尼法的仿真结果和采用有源阻尼法的仿真结果。通过对仿真结果分析得出,采用本文提出的有源阻尼控制策略和电容电流反馈系数设计方法,有源阻尼控制策略取得了和无源阻尼法等效的性能。
[1]BLAABJERG F,TEODORESCU R,LISERRE M.Overview of control and grid synchronization for distributed power generation systems[J].IEEE Transactions on Industrial Electronics,2006,53(5):1398-1409.
[2]PARIKSHITH P,JOHN V.Filter optimization for grid interactive voltage source inverters[J].IEEE Transactions on Industrial Electronics,2010,57(12):4106 -4114.
[3]邓翔,胡雪峰,龚春英.LCL滤波并网逆变电源的控制策略研究[J].电机与控制学报,2011,15(5):37-41.DENG Xiang,HU Xuefeng,GONG Chunying.Study on control scheme for grid-connected inverter with LCL filter[J].Electric Machines and Control,2011,15(5):37 -41.
[4]张兴,张崇巍.PWM整流器及其控制[M].北京:机械工业出版社,2012:256-271.
[5]刘飞,查晓明,段善旭.三相并网逆变器LCL滤波器的参数设计与研究[J].电工技术学报,2010,25(3):110-116.LIU Fei,ZHA Xiaoming,DUAN Shanxu.Design and research on parameter of LCL filter in three-phase grid-connected inverter[J].Transactions of China Electrotechnical Society,2010,25(3):110-116.
[6]阚加荣,谢少军,刘爱忠.逆变器单元用LCL滤波器的并联系统性能分析[J].电机与控制学报,2010,14(2):90-98.KAN Jiarong,XIE Shaojun,LIU Aizhong.Performance analysis LCL filter of parallel system using inverter unit[J].Electric Machines and Control,2010,14(2):90 -98.
[7]WANG T C Y,YE Zhihong,GAUTAM S.Output filter design for a grid-interconnected three - phase inverter[C]//IEEE Power Electronics Specialist Conference 2003,June 15 - 19,2003,Acapulco,Mexico.2003:779 -784.
[8]YI Lei,ZHAO Zhengming.An improved virtual resistance damping method for grid-connected inverters with LCL filters[C]//Energy Conversion Congress and Exposition(ECCE),Sept.17 -22,2011,Phoenix,AZ,United states.2011:3816 -3822.
[9]赵仁德,赵强,李芳,等.LCL滤波的并网变换器中阻尼电阻影响分析[J],电力系统及其自动化学报,2009,21(6):111-116.ZHAO Rende,ZHAO Qiang,LI Fang,et al.Impact of damping resistance on grid inverter with LCL-filter[J].Proceedings of the CSU-EPSA,2009,21(6):111-116.
[10]王要强,吴凤江.阻尼损耗最小化的LCL滤波器参数优化设计[J].中国电机工程学报,2010,30(27):90-95.WANG Yaoqiang,WU Fengjiang.Optimized design of LCL filter for minimal damping power loss[J].Proceedings of the CSEE,2010,30(27):90-95.
[11]LISERRE M,ANTONIO Dell'Aquila.Stability improvements of an LCL-filter based three-phase active rectifier[C]//PESC2002,June 23 -27,2002,Cairns,Australia.2002:1195 -1201.
[12]BLASKO V,KAURA V.A novel control to actively damp resonance in input LC filter of a three phase voltage source converter[C]//Applied Power Electronics Conference and Exposition,Mar.3 -7,1996,San Jose,CA,USA.1996:545 -551.

