面向软性磨粒流加工的流速模糊控制*

计时鸣，周龙兵，谭大鹏，时 梦，张 微

（浙江工业大学特种装备制造与先进加工技术教育部/浙江省重点实验室，浙江杭州，310014）

0 引言

在模具加工领域，为实现对模具中沟、槽、孔等结构化表面的精密加工，出现了磨粒流抛光，例如挤压研磨（AFM）、磨料水射流抛光（AWJF）、磁流变抛光（MRF）、磁射流抛光（MJP）等。这些方法利用磨粒流与加工表面接触时的壁面效应，形成对表面的微切削以实现表面光整加工。但是，由于目前的磨粒流抛光属于“硬性”磨粒流，尚不能获得良好的加工效果，针对“硬性”磨粒流加工的缺点，浙江工业大学计时鸣等人［1-5］提出了“软性”磨粒流加工方法，所谓“软性”磨粒流是指具有弱黏性的液—固两相磨粒流，因此具有更好的流动特性并可实现湍流流动。研究者利用湍流的壁面效应，实现磨粒对工件表面的微力、微量切削作用，以达到精密加工的目的。

在软性磨粒流加工过程中，由于泵的发热以及加工过程本身的发热，随着加工的进行，温度会逐渐升高，导致磨粒流黏度逐渐下降，进而导致工件加工表面加工均匀度的下降。经过前期的研究发现，每个不同的温度下都对应着一个最优流速，使得工件表面加工均匀度较为理想，并得出了温度—最优速度公式。在加工过程中，研究者通过实时地改变磨粒流的流速，使得每个温度下的流速都较为优化，从而提高工件的加工均匀度。由此可见，建立一套自动控制系统是非常必要的。在软性磨粒加工中，动力源为泵，由于加工系统的局限性，一种可行的调速方法就是通过改变泵的转速来改变泵的流量，从而达到改变流道中磨粒流流速的目的。由电机的实际转速公式n=(60f/p)(1-s)可知，改变电源电压的频率，可以改变泵的转速，从而达到控制目的。但是泵的控制问题本身是一个非常复杂的非线性控制问题。而且在磨粒流加工过程中，加工环境复杂，流道中影响磨粒流流速的因素较多，很难以一个精确的数学模型来描述。因此，传统的控制方法难以满足要求。而模糊控制［6］不需要在设计系统时建立被控对象的精确数学模型，只需要积累对加工过程进行控制的操作经验或数据。因而研究者可以针对软性磨粒的加工特性设计一套模糊控制系统［7-12］，以实现流速的自动控制。

本研究利用Matlab 软件中的模糊逻辑控制箱和Simulink 模块，分别对模糊控制器和控制系统进行仿真，从而能更好对所设计的模糊控制系统进行改进，以达到最优的控制效果。

1 模糊控制系统设计

1.1 总体设计

在软性磨粒流加工过程中，加工温度变化范围为20 ℃～60 ℃，最优速度变化范围为75 m/s～125 m/s。一个加工循环为2 h，本研究选定每隔5 min，系统进行一次调速。系统开始运行时，当采样时间到，温度传感器采集当前磨粒流温度，并将数据送入系统，根据温度—最优速度公式计算当前最优速度，并以该速度作为模糊控制器中的给定速度。在模糊控制器内部，速度传感器采集当前的实际速度，实际速度与给定速度之差Δv作为模糊控制器的一个输入量，速度差的变化率Δv′作为另一个输入量，控制器的输出量为电源频率的变化量Δf，执行机构为变频器，最后改变泵的转速。模糊控制系统框图如图1所示。

1.2 模糊控制器设计

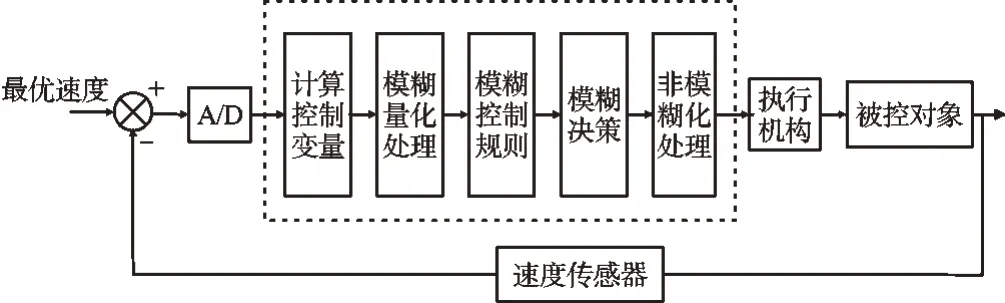
图1 模糊控制系统框图

在软性磨粒流加工过程中，在2 h内，磨粒流温度由20 ℃提升到60 ℃，对应的最优速度由75 m/s 提升到125 m/s，由此可以计算出磨粒流每5 min温度提升1.67 ℃，从温度—最优速度公式可以看出，5 min内，最优速度最大提升值大致为3.3 m/s。根据实验所选择的潜水排污泵的型号以及总结相关经验，电源频率每提升1 Hz，对应的流道中的流速最大提升量为2 m/s，但是实际上很多时候，并不能达到最大值。而模糊控制器输出的精度为0.1 Hz，即流速控制的精度最小也有0.2 m/s，根据模糊控制的逼近特性，事实上控制精度是小于0.2 m/s的，完全满足控制的需求。

根据以上计算，在模糊控制器的设计中，输入量E（即Δv）的基本论域为（-4，4），输入量EC（即Δv′）的基本论域为（-6，6），输出量U（即Δf）的基本论域可以选定为（-2，，2）。理论上来说，输入量、输出量的论域划分越细，那么控制精度就越高，这里输入量E的论域为（-8，-7，-6，-5，-4，-3，-2，-1，0，1，2，3，4，5，6，7，8，），输入量EC的论域为（-6，-5，-4，-3，-2，-1，0，1，2，3，4，5，6），输出量U的论域为（-0.8，-0.7，-0.6，-0.5，-0.4，-0.3，-0.2，-0.1，0，0.1，0.2，0.3，0.4，0.5，0.6，0.7，0.8）。根据基本论域和论域，可以计算得到E的量化因子ke=8/4=2，EC的量化因子kec=6/6=1，U的量化因子ku=2/0.8=2.5。输入量E的语言变量的值分为负很大（NV），负大（NB），负中（NM），负小（NS），零（ZO），正小（PS），正中（PM），正大（PB），正很大（PV），写为｛NV，NB，NM，NS，ZO，PS，PM.PB，PV｝，同样地，EC的语言变量值为｛NB，NM，NS，ZO，PS，PM，PB｝，输出量U的语言变量值为｛NV，NB，NM，NS，ZO，PS，PM，PB，PV｝。

1.3 隶属度函数的确定

在模糊控制的设计过程中，隶属度函数的设计是至关重要的，隶属度函数选择的合理与否，直接关系到模糊控制系统控制性能的好坏。合理的隶属度函数能够提高系统的控制精度，缩短系统的响应时间，不合理的隶属度函数不但不能够获得满意的控制效果，还有可能造成系统的振荡，甚至发散，这是设计者所不愿意看到的。

在传统的隶属度函数设计中，以分布均匀的三角形隶属度函数或高斯型隶属度函数居多。均匀分布的隶属度函数如图2（a）所示。对于一般的模糊控制来说，这种均匀分布的隶属度函数可以满足控制要求。

该设计中，由于系统每隔5 min采样一次，即控制周期为5 min，控制开始时的速度差会比较大，那么此时要以快速缩小速度差为主，当速度差较小时，要以控制精度和稳定为主，防止系统出现超调，甚至振荡。本研究以此为依据，设计不均匀分布的隶属度函数，分别如图2（b）、2（c）、2（d）所示，在远离平衡点，每个模糊子集所占论域区段较大，这样利于快速缩小速度差，在平衡点附件，每个模糊子集所占领论域区段很小，这种分布可使控制器在零点附件的控制动作精确、细腻。

图2 隶属度函数图

1.4 模糊控制规则的确定

模糊控制规则是模糊控制器的核心，它相当于传统控制系统中的校正装置或补偿器，是设计控制系统的主要内容。模糊控制规则的合理与否直接关系着控制性能的好坏。本研究根据软性磨粒流加工的实际经验设计的模糊控制规则表如表1所示。

2 模糊控制系统的仿真

2.1 模糊控制器的仿真

在Matlab 软件中,模糊逻辑工具箱（fuzzy logic toolbox）提供了模糊逻辑控制器及系统设计的各种途径［13］，工具箱提供了图形用户界面编辑函数（GUI），利用它可以直观、迅速地生成系统。本研究利用Matlab软件中的模糊逻辑工具箱建立了对模糊控制器的仿真，模糊控制器如图4 中的“fuzzy logic control”所示，双击进入后分别双击其中的E，EC，U，设置好相应的隶属度函数，并设置好模糊控制规则表对应的63条控制规则。

表1 模糊控制规则表

最后的模糊控制器的输入、输出曲面如图3所示。由输入-输出曲面可以看出，整个曲面较为平滑，说明模糊控制器的设计是较为合理的。

图3 输入-输出曲面

2.2 模糊控制系统的仿真

本研究利用Matlab 软件中的Simulink 模块对整个模糊控制进行仿真，假定某一时刻计算所得的最优速度为80 m/s。模糊控制器的输出量为变频器频率的增量，而由前文计算得到的频率每增加1 Hz，对应的速度输出的最大增量为2 m/s。而由于该系统输出的数学模型包括变频器和泵，总体的传递函数非常复杂，根据输出的频率增量和速度增量为1∶2 的关系可知，输出的频率变化量经过变频器和泵之后转换为流道中流速的增量，这个增量为频率增量的两倍，由此可以看出，变频器和泵综合后的传递函数的增益为2。而变频器和泵中影响系统动态特性的是泵，泵的动力源为电机，电机的传递函数为2阶的，由此可以认为变频器和泵综合后的传递函数也是一个2阶的传递函数。因此可以将传递函数简化为一个大小为2的增益和2阶传递函数1/（S2+S+1）。系统的仿真框图如图4所示。

图4 模糊控制仿真框图

该设计仿真结果及其局部放大图如图5所示。本研究将系统中的模糊控制器中的隶属度函数换成传统的均匀分布的三角形隶属度函数，进行仿真，结果如图6所示。

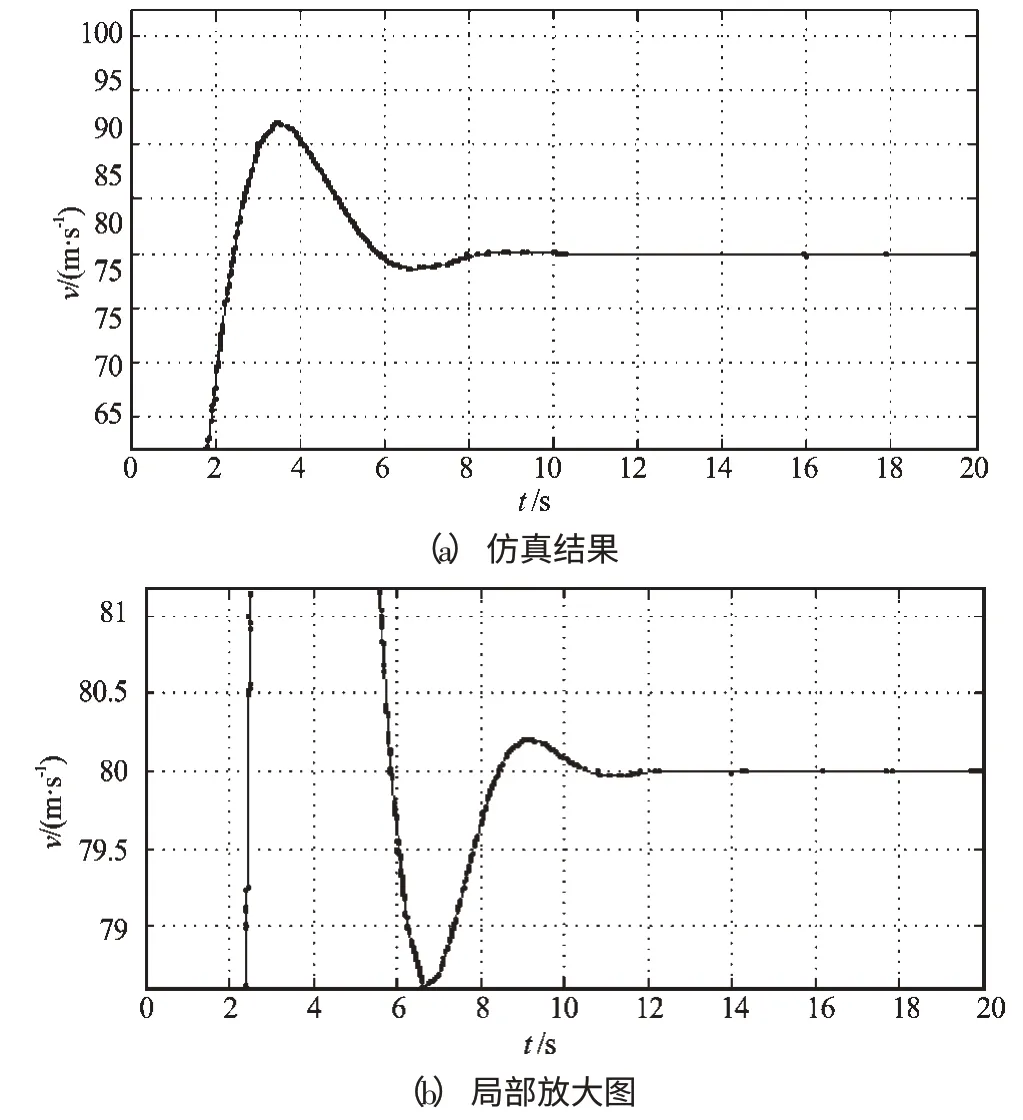
图5 该设计仿真结果及局部放大图

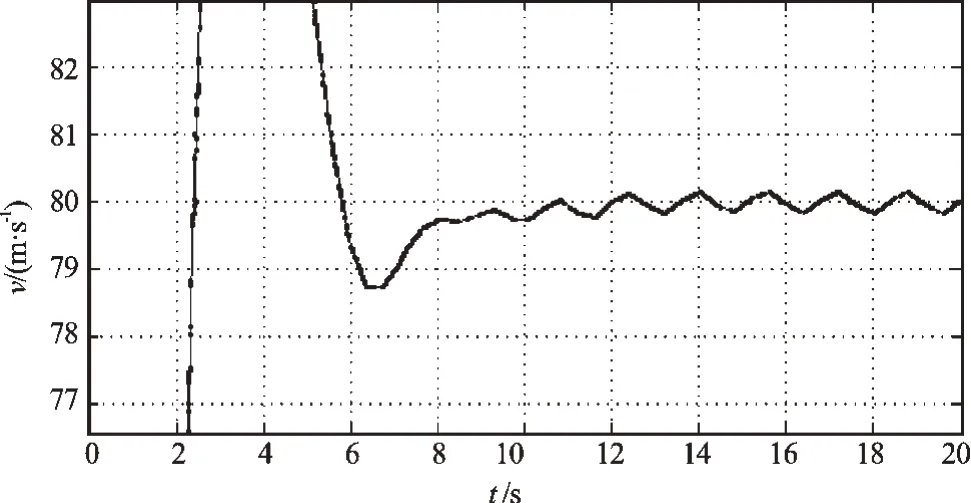
图6 隶属度均匀分布仿真图

通过对比图5、图6，可以看出，采用传统的均匀分布的隶属度函数系统出现了振荡，但是采用本研究设计的隶属度函数，系统没有出现振荡，较快地达到了平衡点，实现了控制目的。仿真结果表明，本研究的模糊控制系统的设计是可行、合理的。

3 结束语

本研究提出了面向软性磨粒流加工的模糊控制系统的设计方法，并对模糊控制器和系统进行了设计，根据软性磨粒流加工的特点，本研究设计了较为合理的隶属度函数和模糊控制规则表。

根据仿真结果可知，与传统的控制方法相对比，本研究设计的模糊控制器具有更好的优越性与合理性。仿真的结果表明，利用模糊控制方法可以实现对软性磨粒流加工自动、连续地控制，而且能达到足够的控制精度。

（References）：

［1］计时鸣，章 定.软性磨粒流精密加工的仿真及实验［J］.机电工程，2012，29（3）：245-248.

［2］计时鸣，赵凌寒，谭大鹏，等.模具结构化表面SAF精密光整技术［J］.机电工程，2011，28（10）：1161-1169.

［3］计时鸣，唐 波，谭大鹏.基于VOF的磨具结构化表面软性磨粒流数值模拟［J］.中国机械工程，2011，22（3）：334-339.

［4］计时鸣，李 琛，谭大鹏，等.基于Preston方程的软性磨粒流加工特性研究［J］.机械工程学报，2011，48（19）：126-130.

［5］计时鸣，兰信鸿.面向固—液两相软性磨粒流嵌入式实时测控系统［J］.机电工程，2012，29（2）：131-135.

［6］刘曙光，王志宏，费佩燕，等.模糊控制的发展与展望［J］.机电工程，2000，17（1）：9-11.

［7］王钢明，任建国，潘晓彬.基于模糊控制的小功率柴油发电机组调速系统［J］.机电工程，2007，24（9）：63-66.

［8］郎 朗，崔 炜，陈跃东.用模糊控制和变频调速实现恒压供水［J］.电子科技大学学报，2004，33（1）：79-82.

［9］叶 军.模糊控制的计算机设计与仿真研究［J］.计算机仿真，2002，19（2）：47-52.

［10］周翼翔，王大贵.发动机冷却液温度模糊控制系统的研究［J］.电子科技大学学报，2009，38（3）：471-474.

［11］陆长明.基于DSP 的超精密抛光机模糊控制系统设计［J］.机电工程，2005，22（12）：11-14.

［12］胡慧琴，李少远.模糊控制系统的解析结构与鲁棒性分析［J］.上海交通大学学报，2005，39（12）：2029-2032.

［13］刘朝英，宋哲英，宋雪玲.Matlab在模糊控制系统仿真中的应用［J］.计算机仿真，2001，18（3）：10-14.