基于CORDIC算法的高速ODDFS电路设计
戈华,聂阳
(集宁师范学院 物理系,内蒙古 集宁 012000)
随着现代通信的高速发展,高精度的正交三角信号广泛应用在频率转换电路中。目前产生正交三角信号的主要的方法是使用直接数字频率合成器 (Direct Digital Frequency Synthesizer,DDFS)。DDFS中频率控制字提供周期性的相位数字序列,在参考时钟的作用下这些相位作为地址信号来读取存储在ROM中三角函数的波形幅度值。然而,随着存储的波形数据和地址信号位数不断增加的,电路会消耗大量的硬件资源。
文中采用CORDIC算法代替ROM储存表结构,并实现正弦和余弦正交三角的函数信号电路。
1 CORDIC算法简介
CORDIC算法是J.E.Volder在进行航天飞行控制系统设计时提出[1],它是一种迭代算法,在实现过程中利用移位和加法运算来代替乘法运算,因此特别适合于硬件实现。假设初始向量 OW1(x,y)旋转 θ角度后得到向量 OW2(x1,y1),如图1所示。
由三角函数得:

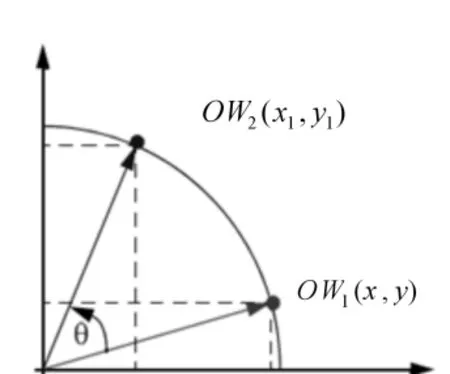
图1 向量旋转θ角度Fig.1 Vector rotationθangle
假设经过i次旋转后角度为θi,xi+1和yi+1分别为:
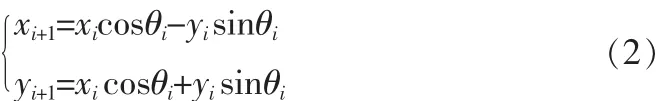
对 θi进行一定的限制[2-3],令 tanθi=2-i,即 θi=arctan2-i。 旋转角度的总和时表示向量逆时针旋转,di=-1时表示向量顺时针旋转。Ki为伸缩因子,表示每次旋转时向量模长发生的变化。
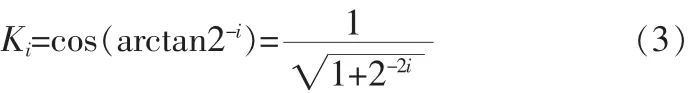
如果位宽一定,旋转次数趋于无穷大时,总的伸缩因子K为:
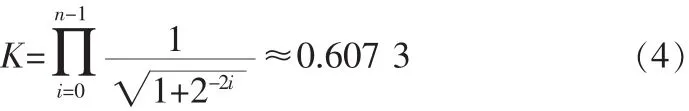
为了使算法的迭代实现更具有实用性,用zi表示第i次旋转后剩余的角度值,这样每次的迭代运算可以简化为:
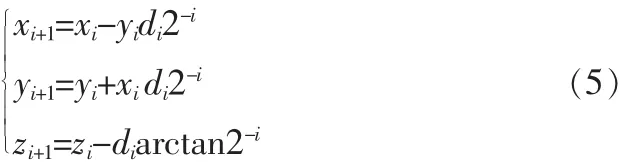
根据式(5)可知CORDIC算法的多级迭代运算电路主要由加、减法运算器和移位寄存器构成,非常适合于FPGA设计与实现,具体设计结构原理如图2所示。
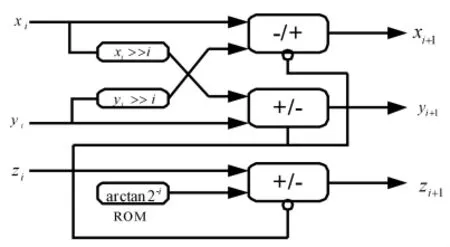
图2 CORDIC算法结构原理图Fig.2 Structure diagram of CORDICalgorithm
2 ODDFS电路设计
整个ODDFS电路由相位累加器、相位加法器、相位幅值转化器、CORDIC处理单元4个基本模块构成,结构如图3所示。

图3 ODDFS电路结构图Fig.3 Structure diagram of ODDFScircuit
相位累加器是ODDFS电路的核心,在参考时钟作用下对频率控制字不断进行线性累加,当累加器输出溢出时,就完成一个周期。累加器的输出数据代表了正余弦曲线的相位。
相位加法器通过改变相位控制字可以控制输出信号的相位,相位累加器的输出与相位控制字的代数和作为相位幅值转换单元的地址数据,使输出的信号产生了不同的相移。
CORDIC处理单元包含相位象限处理单元和相位幅值转换单元。通过CORDIC算法可以实现(-99.9°,99.9°)内的正余弦值的计算。将累加器输出的最高两位用于表示相位所在的象限。通过目标角度进行预处理,可以在原有旋转角度的基础上再添加两级迭代,实现输出(-189.9°,189.9°)所有象限内的正余弦值。相位幅值转换单元存储正余弦信号值作为基本幅值信号输出给相位幅值转化器。
相位幅值转化器之后插入一个幅值乘法器,通过幅度控制字对输出的幅度编码进行幅值调制,生成不同幅度的正余弦信号。
3 ODDFS电路仿真
在MATLAB2012a平台下利用Xilinx公司的SystemGenerator DSP开发工具,采用XILINX的xc3s500e-4fg320 FPGA作为验证平台,在ISE14.1中进行综合、实现、布局布线,最后使用Modelsim6.6a进行电路的时序仿真,电路的功能仿真和时序仿真如图4和图5所示。
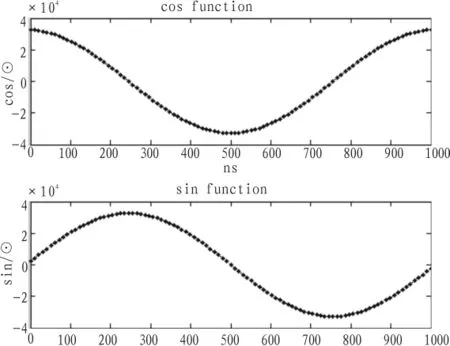
图4 ODDFS电路功能仿真Fig.4 Functional simulation of ODDFScircuit

图5 ODDFS电路时序仿真Fig.5 Timing simulation of ODDFScircuit
4 结 论
文中利用CORDIC算法进行的ODDFS电路设计和建模仿真,实现了ODDFS电路的基本功能,采用FPGA为验证平台,在MATLAB2012、Xilinx System Generator DSP完成的电路的验证。仿真结果表明,系统不但满足高速信号处理的要求,而且具有很高的实用价值。
[1]Volder JE.The CORDIC trigonometric computing technique[J].IRE Trans.Electronic Computers,1959:330-334.
[2]Haviland G,Tuszynski A.A CORDIC arithmetic processor chip[J].IEEE Transaction on Computers,1996:68-79.
[3]Volder J E.The birth of CORDIC[J].Journal of VLSI Signal Processing,2000:101-105.
[4]Srikanthan T,Gisuthan B.A novel technique for eliminating iterative based computation of polarity of micro rotations in CORDIC based sine-cosine generators[J].Microprocessors and Microsystems,2002:243-252.
[5]Kebbati H S,Blonde J Ph,Braun F.A new semi-flat architecture for high speed and reduced area CORDIC chip[J].Microelectronics Journal,2006:181-187.
[6]Juang T T B,Hsiao S F,Tsai M Y.Para-CORDIC:parallel CORDICrotation algorithm[J].IEEE Transactions on Circuits and Systems I,2004:1515-1524.

