一种带振幅调节的晶体振荡器
向延钊, 张 涛, 张 迪
(1.武汉科技大学 信息学院,湖北 武汉 430080;2.德鑫微电子公司 湖北 武汉 430070)
晶体振荡器能够给电子系统提供高精度的时钟基准,多采用Pierce结构集成到芯片当中。现在振荡器的性能主要体现在频率稳定性和功耗上。采用固定的偏置电流能提高频率稳定性,但是偏置电流过大会引起与设计频率的偏差,也会带来大的功耗问题。而电流过小,会导致振荡器启振过慢或是不能启振。为了得到稳定的输出频率,传统的Pierce晶体振荡器电路都需要一个远大于晶振内阻的电阻来保证振荡器频率远高于电路谐振频率[1]。无论有无大的电阻工艺,直接做大电阻会占用较大的面积。针对上述所提到的问题,文中设计了一种改进型的Pierce电路,增加了振幅调节,于振荡电路构成一个环路。降低了功耗提高了频率稳定性。另外独立的电流源下的MOS管有源电阻可以充分的减少版图面积,并且提高电压抑制比。
1 Pierce振荡器原理
1.1 基本结构分析
单管(源接地)作放大管的Pierce振荡器如图1所示,它由晶振、MOS管、和电容C1、C2构成,偏置电路部分已省去。其小信号等效电路如图2(a)所示。图中的Lm、Cm、Rm构成晶体振荡器的主要等效参数,等效阻抗为Zm。虚线右边的电路以及晶体谐振器等效的并联电容构成等效阻抗Zc。可以把Zc等效为一个负电阻 Re(Zc)和一个容抗 Im(Zc)[2],如图 2(b)所示。


图1 Pierce振荡器电路Fig.1 Pierce oscillator circuit

图2 晶体振荡器小信号等效模型和简化模型Fig.2 Small-signal equivalent model and the simplified model of crystal oscillator
由于 Z1、Z2、Z3是容性阻抗,且 Re(Zc)为负数。 由此可以得到振荡平衡条件:Zm+Zc=0。大致的Zc(Gm)复平面轨迹如图3所示。虚线对应的是晶振的-Rm,与Zc复平面轨迹交点为A、B。A点为振荡稳定点,对应的无损电路跨导:

其中,C3为晶振电路并联部分,Z3的容抗点是平衡振荡条件下的另一个解,是一个不稳定点,是能振荡条件跨导的最大值。复平面最左边是振荡电路达到的最大负阻,无损电路最大负阻:


图3 Z c复平面轨迹Fig.3 Complex plane trajectory of Z c
振荡器能启振必须满足条件:|Rn0|max>Rm否则振荡器负阻无法抵消晶振的内阻而达到稳定的振荡点。
1.2 振幅与偏置电流关系
对于振荡器功耗考虑,选择晶体管工作在弱反型区。这里强调的是电路的非线性对振荡器是必须的。晶振等效模型拥有非常高的品质因数Q,所以流入到晶振等效模型的Im是正弦的,如图 2(b)所示。Im=-Ic,由于非线性的作用,|I c|的变大导致跨导Gm逐渐变小,直到处于振荡平衡点。栅极的电压也可以看成是一个正弦波。漏电流的表达式[3-4]:

其中 Ispec=2nμCox,VG为栅极电压的直流分量,|V1|为栅极电压交流分量的振幅。VT=KT/q为热力学电压,n为晶体管的斜率因子。由上式可以得到直流跨导:

可以知道在弱反型区直流跨导与偏置电流成正比。结合式(2)可以得到临界电流I0critmin。如果采用固定的电流偏置,电流过小,振荡器启振困难或不启振。电流过大,振荡器快速启振,但非线性产生的谐波分量通过增加损耗来降低负阻。另外这些谐分量会产生新的不同的电流谐分量而影响Zc的虚部。这样也难以掌控所设计的振荡频率。偏置电流临界电流和栅极电压振幅的关系:

其中 IB0(V1)、IB1(V1)以此是关于 V1的零阶和一阶修正贝塞尔函数。可以得到偏置电流和栅极电压振幅近似于正比关系。这样我们就可以通过一个振幅检测来控制电流大小构成一个闭环系统(如图4所示)。如图5所示,I0随着|V1|的增大而减小,I0critmin由于非线性作用增大,振幅调节过程中相交于P点而达到稳定。相对于未加振幅调节的Q点,非线性减小,频率稳定性加强,偏置电流减小,功耗降低。

图4 振幅调节闭环系统Fig.4 Amplitude adjustment of the closed-loop system
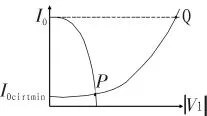
图5 比较曲线Fig.5 Comparison of the curve
1.3 MOS管电阻和振幅调节原理
对于振幅控制,先采用电阻的模型来分析,如图6所示。电阻R跨接在栅漏两端,因为没有直流通路,A、B两点的直流电压相等。振荡信号Vin经过Ca隔直后到达M的栅极。滤波电容Cb不可能做的太大,所以在B点还有一定的交流电压。但是对A点交流振幅对B点直流电压的分析影响很小。因为没有其他的直流通路,所以M的平均电流就等于直流偏置电流 I,考虑式(4),可得到[5]:

上式表明:偏置电流I不变,振幅减小,栅极电压升高;振幅增加,栅极电压降低。因为B点受交流信号影响很小,所以其电压近似于栅极直流电压。因此,振幅的变化可以反映到B点电压变化上来。

图6 振幅控制原理图Fig.6 Schematic of amplitude control
振荡器漏栅之间的电阻必须足够的大保证振荡频率远大于电路谐振频率,另外检测电阻阻值相对也比较大。实际电路中为了减小面积尽量避免使用电阻而用MOS管电阻代替,如图7所示。V1、V2表示Tb两端交流电压。MOS管组成的线性电阻成立的条件是V1与V2大小相接近并且反相。假设两只管子都强反型,Tb处于饱和区,而Ta处于三极管区。Ta、Tb有共同的栅极电压,可以得到:

图7 MOS管电阻部分结构Fig.7 Part structure of MOSresistor

这样可以推导出点电阻:

其中Kr为管子的转移参数比率为反型系数。
2 电路设计分析及仿真结果
图8是根据上述原理设计的电路,按照虚线标记分成3部分:

图8 带振幅调节振荡器原理图Fig.8 Oscillator schematic with amplitude regulation
Ⅰ部分是电流参考源, 主体部分由 M2、M3、M5、M6、R1构成,两n管的个数比、n管长宽比以及电阻大小决定参考电流大小。M1、M4、C7构成了一个软启动电路克服电流参考电路启动问题。电源上电时,C7上端未被充电,M4栅极电压为低而导通,通过 M4、M5、M6电压被抬高使主体部分电路工作,M3反馈过来的降低电压使M1导通对C7充电,当达到一个高的电位时,M4被截止,启动电路停止工作。滤波电容C6起电压缓冲的作用,防止大的电流出现[6]。
Ⅱ为振幅检测与电流偏置部分,X1端的振荡信号通过电容C4、C5传递到M12的栅极,电阻用MOS管电阻代替。通过上面原理所分析的,M12栅极交流电压会影响到漏极电压的大小,再通过 M13、M14、M15来控制偏置电流[7]大小。
Ⅲ为基本振荡器电路,电阻用MOS管电阻代替温度变化会直接影响阻抗虚部的变化,考虑到电路振荡的稳定性,虚部越小越好,就是要求C1、C2越大越好,但是考虑到取得的最大跨导,C1、C2要尽量的小并且大小相差不大。折中考虑,C1=C2=25 pF。为了保证低功耗[8],参考电流也应该很小,这要求足够大的电阻和大的n管数量比。
在0.35μm、5 V CMOS工艺下,通过Spectre对电路仿真得到波形图9、图10。在图9中可以看到振幅调节过程。启振时,偏置电流为480 nA,振幅增加,偏置电流变小,电流最终维持在130 nA。振幅最终稳定在400 mV左右,如图10所示。

图9 振荡器的偏置电流Fig.9 Bias current of the oscillator

图10 振荡器输出电压(X1)Fig.10 Oscillator output voltage (X1)
3 结 论
带振幅调节控制的Pierce振荡器有效地降低了功耗并提高了振荡器的稳定性。采用MOS管电阻有效地节省了版图面积。实测结果表明:5 V工作环境下,振荡器工作电流约为300 nA,并且能稳定工作在1~5.5 V的范围内,满足使用要求,达到了预期效果。
[1]Rusznyak A.Start2up time of CMOS oscillators[J].IEEE Trans on Circuits and Systems,1987,34(3):259-268.
[2]Vittoz EA,Degrauwe M GR,Bitz S.High-Performance crystal oscillator circuits:theory and application[J].IEEE JSSC,1988,23(3):774-783.
[3]Vittoz E,Fellrath J.CMOS analog integrated circuits based on weak inversion operation[J].IEEE JSSC,1977,SC-12(3):224-231.
[4]Wey T.On amplitude and operating point control of a voltage-ontrolled crystal oscillator[J].Midwest Symposium on Circuits and Systems,2007(50):221-224.
[5]Eric Vittoz.Low-Power Crystal and MEMS Oscillators[M].New York:Springer,2010:41-135.
[6]PENG Zheng-hong,LIU San-qing,ZOU Xue-cheng.Design of agood stable32.768 kHzquartzcrystal oscillator[J].Computer&Digital Engineering,2004,32(1):73-75.
[7]马天祥,徐岩.基于电流故障分量比相法的变压器后备保护[J].陕西电力,2011(7): 49-52.MA Tian-xiang,XU Yan.Transformer backup protection based on current fault component phase comparison[J].Shaanxi Electric Power,2011(7):49-52.
[8]章吉刚,蒋桂香.高精度低功耗数字光衰减器设计与实现[J].工业仪表与自动化装置,2010(5):102-104.ZHANGJi-gang,JIANGGui-xiang.The design and implement of the high precision and low power digital optical attenuator[J].Industrial Instrumentation&Automation,2010(5):102-104.

