基于模糊PID控制MPPT在光伏系统中的仿真研究
陈丽,韩辉
(沈阳工业大学 信息工程学院,辽宁 沈阳 110870)
在当今油、碳等能源短缺的现状下,各国都加紧发展新能源的步伐,而太阳能光伏发电在21世纪会占据世界能源消费的重要席位,不但要替代部分常规能源,而且将成为世界能源供应的主体。然而,如何提高光伏发电的效率,是研究者一直热点讨论的问题。
光伏电池的材料大部分为晶硅光伏组件,其输出功率易受太阳辐照度和组件温度的影响。不同的辐照度和温度下输出功率也会发生变化。为了系统能够在任意的太阳辐照度和温度下始终保持最大功率输出,需要对该条件下的最大功率点(Maximum Power Point,MPPT)进行追踪。
目前,常用的技术有恒定电压控制法、扰动观察法、电导增量法、模糊控制法、神经网络法等[1-3]。恒定电压控制法,控制简单,易于实现,有很好的稳定性,但精度较差,特别是外界环境发生变化时,对最大功率点变化适应性差;扰动观察法速度快,易于实现,但稳态精度不高,工程上常常采用此种控制算法;电导增量法控制效果好,稳定度高,但进行控制时需要较多的运算判断,控制算法相对比较复杂,同时对控制系统要求较高;神经网络法,算法比较复杂,实现相对较难,并且需要长时间的训练。综合考虑,文中介绍一种基于模糊PID控制MPPT方法。根据光伏电池的输出特性,运用MATLAB建立了光伏阵列仿真模型,并对MPPT进行仿真。
1 光伏电池的数学模型
光伏电池的等效电路为:

图1 光伏电池等效电路Fig.1 Equivalent circuit of the solar cell
由图1等效电路图可得:

式中,Iph为光生电流;Io为二极管反向饱和电流;q为电子电荷(1.6×1019C);K 为玻尔兹曼常数(1.38×10-23J/K);T 为绝对温度;A为二极管因子;Rs为串联电阻;Rsh为并联电阻。
根据式(1)的基础上,文献[4]对其进行简化处理,得到工业用的数学模型:

以上模型在得知短路电流Isc、开路电压VOC、最大功率点时的电流Im、最大功率点时的电压Vm就能在一定精度条件下,得到太阳能光伏特性。
在任意 环境条件 下,Isc、VOC、Im、Vm会按 一定规律 发生变化。通过引入相应的补偿系数,近似推出任意太阳辐照度和温度下4个技术参数[5]。
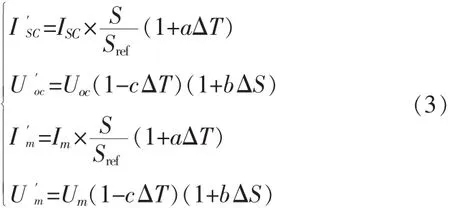
其中

式中Tref=25℃为参考电池温度;Sref=1 000 W/m2为参考太阳辐照度;补偿系数a、b、c为常数,根据大量实验,得出
a=0.002 5;b=0.000 5;c=0.002 8。
根据以上公式即可以计算出在任意太阳辐照度S和电池组件温度T条件下太阳能电池输出特性。
2 模糊PID控制器的设计
由于太阳能电池的非线性,用精确的数学模型无法表示,系统存在较大的复杂性和不确定性,可以运用模糊PID控制方法实现最大功率点的跟踪。这里选择二维模糊控制器,模糊PID控制器的结构如图2所示。

图2 模糊PID控制器结构图Fig.2 Structure drawing of fuzzy-PID controller
由图可知输入量与反馈量的偏差e和偏差变化率ec乘以量化因子转换成模糊控制器的两个输入,然后模糊控制器经过模糊推理,解模糊化,乘以比例因子转换为PID控制器中比例积分微分系数的变化量 ΔKP、ΔKi、ΔKd,与初始 PID 参数相加得到新的PID参数,然后通过PID控制器计算出控制量 u(t),对被控对象进行控制。
2.1 模糊化和隶属函数的建立
取输入 e 和 ec 和输出 ΔKP、ΔKi、ΔKd, 模糊子集为{NB,N M,NS,ZO,PS,PM,PB},子集中元素分别代表负大,负中,负小,零,正小,正中,正大,其论域为[-3,3]。 在模糊逻辑工具箱的隶属度函数编辑器中,选择输入量e,ec的隶属函数为三角形(trimf),输出 ΔKP、ΔKi、ΔKd的隶属函数为三角形(trimf),如图 3和图4所示[6]。

图3 e及ec隶属度函数Fig.3 e and ec membership function
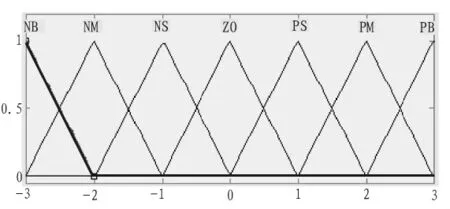
图 4 ΔK P、ΔK i、ΔK d隶属度函数Fig.4 ΔK P、ΔK i、ΔK d membership function
2.2 模糊化规则的建立
根据参数KP、Ki、Kd对系统输出特性的影响,可归纳出系统在被控过程中对不同的偏差和偏差变化率,参数KP、Ki、Kd的自整定原则[7]:
1)当偏差较大时,为了加快系统的响应速度,并防止因开始时偏差的瞬间变大可能引起的微分过饱和而使控制作用超出许可范围,应取较大的 KP和较小的 Kd。另外为防止积分饱和,避免系统响应出现较大的超调,Ki值要小;
2)当偏差和变化率为中等大小时,为了使系统响应的超调量减小和保证一定的响应速度,KP应取小一些。在这种情况下Kd的取值对系统影响很大,应取小一些,Ki的取值要适当;
3)当偏差较小时,为了使系统具有较好的稳态性能,应增大KP、Ki值,同时为避免输出响应在设定值附近振荡,以及考虑系统的抗干扰能力,应适当选取Kd,其原则是:当偏差变化率较小时,Kd取大一些;当偏差变化率较大时,Kd取较小的值,通常Kd为中等大小。
从而可得模糊控制规则如表1~表3所示。
2.3 推理算法和解模糊化算法的设计
在MATLAB命令窗口运行Fuzzy进入模糊逻辑编辑器,并建立一个新的FIS文件,选择控制器类型Mamdani,推理(implication)方法选为 min,解模糊化(defuzzification)方法为重心平均法centroid,如图5所示。

表1 ΔK P的模糊控制规则表Tab.1 Fuzzy control rules ofΔK P

表2 ΔK i的模糊控制规则表Tab.2 Fuzzy control rules ofΔK i

表3 ΔK d的模糊控制规则表Tab.3 Fuzzy control rules ofΔK d
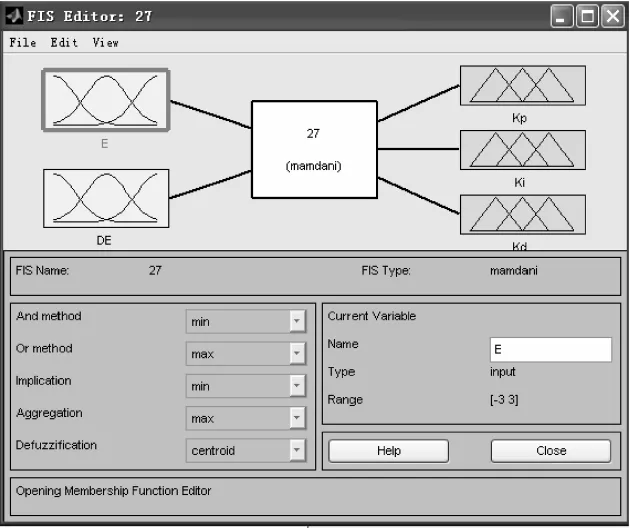
图5 清晰化的方法Fig.5 Certainty of outputs
3 仿真研究
用Matlab对太阳能光伏系统进行仿真,仿真模型及仿真图如图6、7所示。
模糊化因子 Ke=10,Kec=10,解模糊因子 K1=1,K2=1,K3=1,PID 初始值 Kp=100,Ki=8,Kd=30。
根据在的标准测试条件(Tc=25℃,S=1 000 W/m2)所选的光伏电池参数分别为 Pm=89 W,Um=42.3 V,Im=2.12 A,UOC=45.3 V,ISC=2.12,仿真结果如图8所示。
当光照强度在0.1 s时,光照强度从300 s/m2跃变到1 000 s/m2时对系统做出仿真,仿真结果如图9所示。
由图可知,系统的反应速度快,稳态特性良好,系统精度的精度较好,在最大功率点的振荡小,并且能够迅速对环境变化做出反应,稳定工作在最大功率点处。
4 结 论
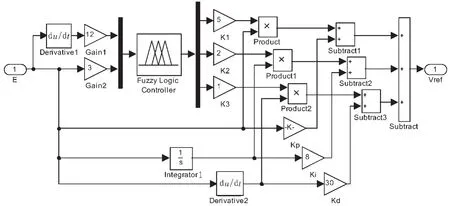
图6 模糊PID控制器仿真模型Fig.6 Simulation model of fuzzy PID controller

图7 模糊PID控制系统仿真图Fig.7 Simulation drawing fuzzy PID control system

图8 光伏电池功率曲线Fig.8 Power curve of the solar cell

图9 光伏电池功率曲线Fig.9 Power curve of the solar cell
针对光伏电池的输出特性易受外界环境影响,需对其进行最大功率跟踪,由于光伏系统为非线性系统,很难建立精确的数学模型,运用模糊PID控制很好的解决这一问题。仿真结果验证了该控制器响应速度快,精度高,稳态性能好,当外界条件变化后,能快速响应,对提高光伏系统的效率有着重要意义。
[1]程启明,程尹曼,王明媚,等.光伏电池最大功率点跟踪方法的发展研究[J].华东电力,2009,37(8):1300-1306.CHENG Qi-ming,CHENG Yin-man,WANG Ming-mei, et al.Review on the MPPT method of PV battery[J].East China Electric Power,2009,37(8):1300-1306.
[2]崔岩,蔡炳煌,李大勇,等.太阳能光伏系统MPPT控制算法的对比研究[J].太阳能学报,2006,27(6):535-539.CUI Yan,CHAI Bing-huang,LI Da-yong, et al.Comparative studies on the MPPT control algorithms of solar energy photovoltaic system[J].Acta Energiae Solaris Sinica,2006,27(6):535-539.
[3]李晶,窦伟,徐正国,等.光伏发电系统中最大功率点跟踪算法的研究[J].太阳能学报,2007,28(3):268-273.LI Jing,DOU Wei,XU Zheng-guo,et al.Research on MPPT methods of photovoltaic power generation system[J].East China Electric Power,2007,28(3):268-273.
[4]苏建徽,余世杰,赵为,等.硅太阳电池工程用数学模型[J].太阳能学报,2001,22(4):409-412.SU Jian-hui,YU Shi-jie,ZHAO Wei,et al.Investigation on engineeringanalytical model of silicon solar cells[J].East China Electric Power,2001,22(4):409-412.
[5]YushaizaDY,Sitihs,Muhammad A L.Modeling and simulation of maximum power point tracker for photovoltaic system[C].National Power&Energy Conference,2004(29-30):88-03.
[6]吴振顺,姚建均.模糊自整定PID控制器的设计及其应用[J].哈尔滨工业大学学报,2004(36):576-580.WU Zhen-shun,YAO Jian-jun.A self-tuning fuzy PID controller and its application[J].Journal of Harbin Institute of Technology,2004(36):576-580.
[7]刘绍鼎,樊立萍,姜长洪.基于模糊规则参数自整定PID控制器的设计[J].微计算机信息,2007,23(4-1):50-52.LIU Shao-ding,FAN LI-ping,JIANG Chang-hong.Design of parameter auto-tuning PID controller based on fuzzy rules[J].Microcomputer Information,2007,23(4-1):50-52.

