一种简化PID模糊控制器的研究与设计

雷春雨，王 直

（江苏科技大学 江苏 镇江 212003）

美国加州大学控制论专家L.A.Zadeh教授于1965年创立了模糊集理论，为描述研究和处理模糊性现象提供了有力的数学工具。继Zadeh 1973年提出模糊控制思想后，1974年英国的 E.H.Mamdani教授在实验室将模糊逻辑在锅炉和蒸汽机的控制上得到成功应用，标志着模糊控制的诞生[1]。此后的40多年里，模糊控制技术得到了飞速的发展，得到众多学者的关注和重视。

模糊控制器虽然与常规PID控制器在控制机理方面有许多相似之处，但是模糊PID是智能PID，具有自适应性。而常规PID控制器属于线性控制的范畴。目前人们常采用的模糊控制器大多是二维的，常见的两种二维模糊控制器为PD型和PI型。相比而言，PD型模糊控制器的优点是动态控制品质较好，缺点是在稳态时，系统输出偏差较大；PI型虽然稳态偏差优于PD型，但就整个动态过程并不及PD型。为了稳态和动态能同时保持良好的品质性能，人们研究出了三维的PID型模糊器[2]。所谓三维就是将模糊控制的控制规则有3个输入变量，这样的处理虽可以使模糊控制系统的性能提高，但是由于规则的输入变量增加了，模糊控制规则数也相应增加，这就给建立和完善三维模糊控制规则库带来了很大的困难。文中就将推导一种简化PID型模糊控制器，它不仅具有三维PID型模糊控制器的性能，而且只需采用两个输入变量和一个模糊规则库，这样将大大减少模糊控制规则数。

1 模糊控制器的基本原理和结构分类

模糊控制器主体部分是由计算机或单片机构成，多采用二维模糊控制结构，实现一步模糊控制算法的过程描述如下：计算机采集被测参数的精确值，然后将此值与给定值作比较，得出误差e以及误差变化率ec作为模糊控制器的输入语言变量，将e和ec经模糊化处理得到E和EC，并用相应的模糊语言表示，由此便得到了相应的模糊子集。再由E模糊子集和模糊控制规则，根据推理的合成规则进行模糊决策，得到模糊控制量U，解模糊化化得到精确控制量u[3]。

在众多种类的模糊控制器中，二维模糊控制器由于其输入变量合理、规则库易于建立而得到广泛的应用。这里仅介绍2种常用的二维模糊控制器：一种是PD型模糊控制器，如图1所示；另一种是PI型模糊控制器，如图2所示。

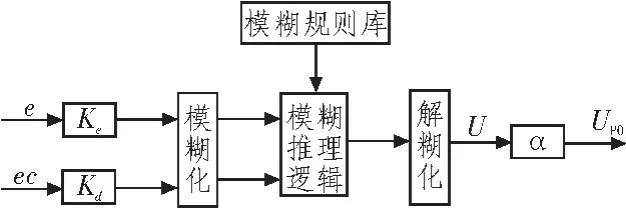
图1 PD型模糊控制器Fig.1 PD fuzzy controller

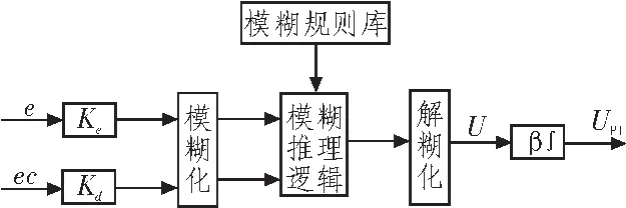
图2 PI型模糊控制器Fig.2 PIfuzzy controller

它们两者的差别主要表现在输出量和规则库的建立。PD型模糊控制器直接为输出控制量，而PI型模糊控制器的输出一般是控制量的增量形式[4]。由于输出量不同，所以它们具体规则库的形式也不同。

为了减少PID型模糊控制器控制规则的数量，同时又克服PD型和PI型模糊控制器的缺点，首先想到是将上述2个模糊控制器并联在一起，构成一个二维输入的PID型模糊控制器，如图3所示。

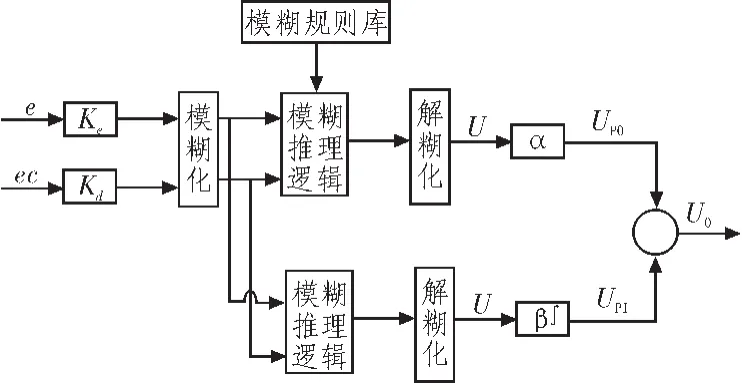
图3 并联PID型模糊控制器Fig.3 Parallel PID fuzzy controller

较之传统的三维PID型模糊控制器，这种方案只要需2个二维输入的控制规则库，就可实现PID型模糊控制器。虽然控制规则数有所减少，但仍需要建立2个，这在实际应用中还是相对比较麻烦。本文接下来将研究推导出一种简化二维PID型模糊控制器。

2 简化PID型模糊控制器

为了进一步降低规则库建立的复杂程度，可以考虑在PD型模糊控制器后面并联一个积分环节，同时引入2个权重系数α和β，如图4所示。从理论上证明，此简化的模糊控制器可等效为一个时变非线性PID型模糊控制器，与传统的PID型模糊控制器相比，它只需2个输入变量和一个规则库[5]。下面是该模糊控制器的推导过程。

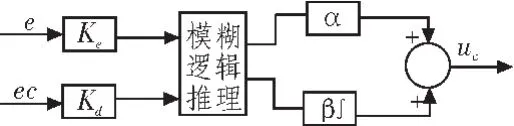
图4 简化PID型模糊控制器Fig.4 Simplified PID fuzzy controller

该模糊控制器的两个输入分别为 e（误差），ec（误差变化率），输出为 u（控制量）。 e，ec，u 的离散论域分别为 E⊂R，EC⊂R，U⊂R。 e 和 ec 的模糊集合分别 Ai（i∈I=[-m，...，-3，-2，-1，0，1，2，3，...m]）和 Bj（j∈J=[-n，...，-3，-2，-1，0，1，2，3，...，n]）。

已知PD型模糊控制器的输出为：

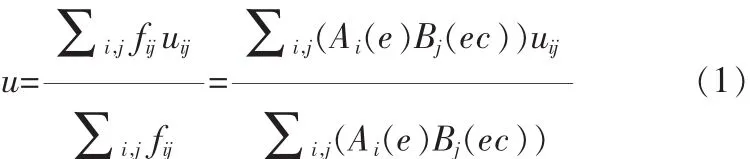
现在假设某 t时刻，输入 e在区间[ei，ei+1]内，ec在区间[ecj，ecj+1]内，此时，e，ec 的率属度分别为

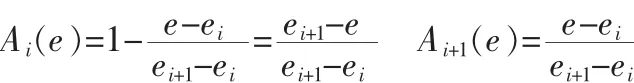
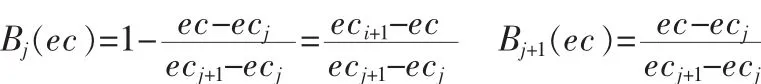
由于在任一时刻，输入e和ec的率属函数最多只在两相邻的模糊子集上不为0，即：

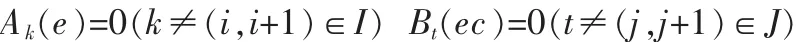
所以，式（1）可化简为

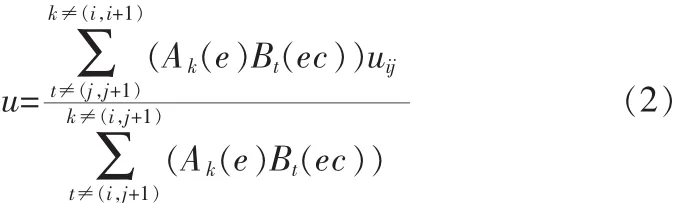
当 e∈[ei，ei+1]时有 Ai（e）+Ai+1（e）=1

当 ec∈[ecj，ecj+1]时有 Bj（ec）+Bj+1（ec）=1

由此，式（2）可进一步化简为

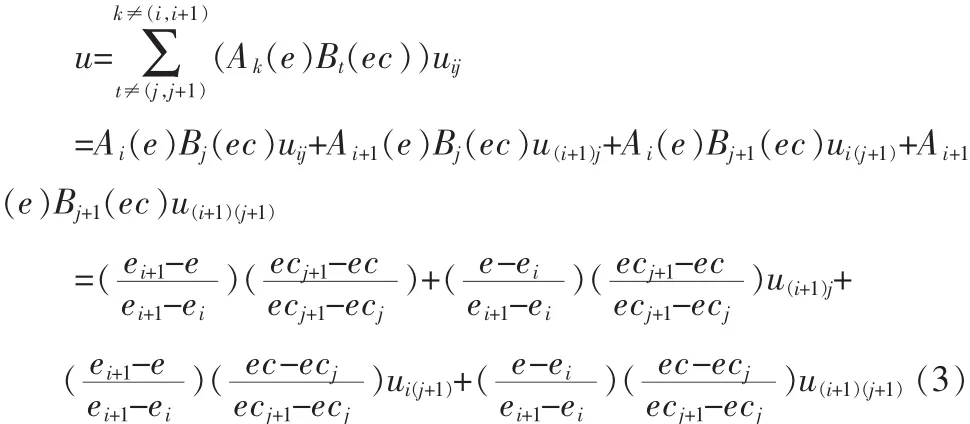
由式（3）可知，控制器的输出u是输入e和ec的非线性函数：

同时又定义：

若 δe，δec，δu 足够小，且（ei+δe，e+δec）∈[ei，ei+1]×[ecj，ecj+1]，则式（4）可用下式来表示：

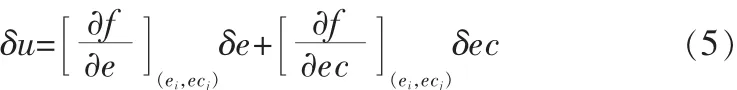
由式（3）整理得：

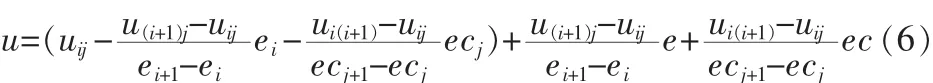
最后得简化PID模糊控制器的输出为：

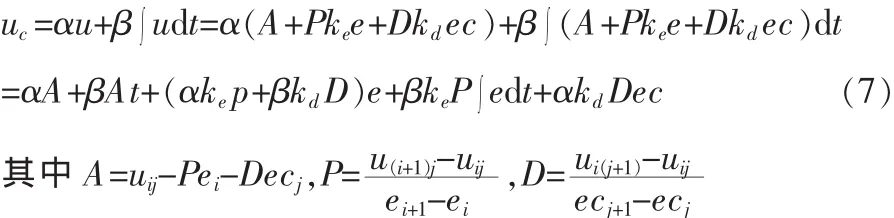
此PID型模糊控制器可通过调整2个权重系数α、β来进行PI型和PD型模糊控制器之间的切换：

当α>0，β=0时，为 PD型模糊控制器；

当α=0，β>0时，为 PI型模糊控制器；

当α>0，β>0时，为 PID型模糊控制器。

3 仿真结果

为了验证上述简化PID型模糊控制器的性能，将其与PD及PI型模糊控制器进行仿真比较。

从传统的控制理论中我们知道，控制对象大多为0型系统。因此，考虑用一个二阶线性系统来验证简化 PID型模糊控制器的性能[6]。二阶对象的传递函数为：

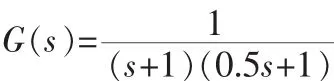
输入e、ec和控制输出 u的隶属度函数如图5所示。PI型模糊控制器控制规则如表 1所示，PD型模糊控制器的控制规则如表 2所示。简化PID型模糊控制器的规则与PI型相似。模糊控制器采用MATLAB的模糊控制工具箱设计，并在 Simulink[7]中调用。

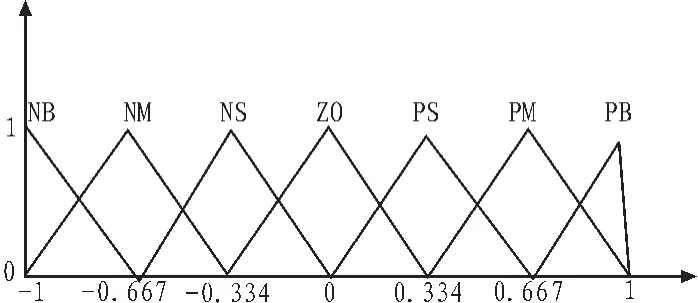
图5 e，ec和 u的隶属度函数Fig.5 Membership functions of e，ec and u

其中 {NB，NM，NS，Z0，PS，PM，PB}表示 {负大，负中，负小，零，正小，正中，正大}。

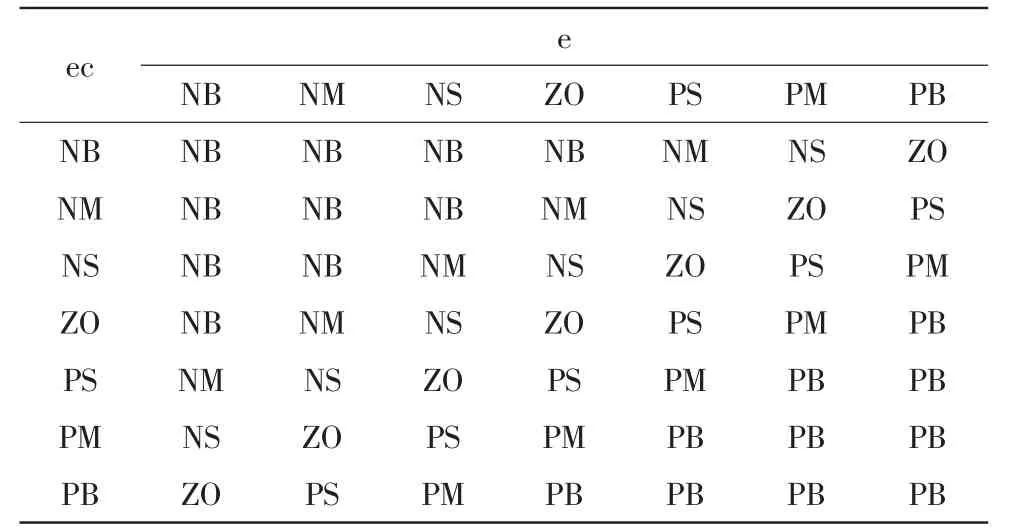
表1 PI/PID型模糊控制规则表Tab.1 Table of PI/PID fuzzy control rules

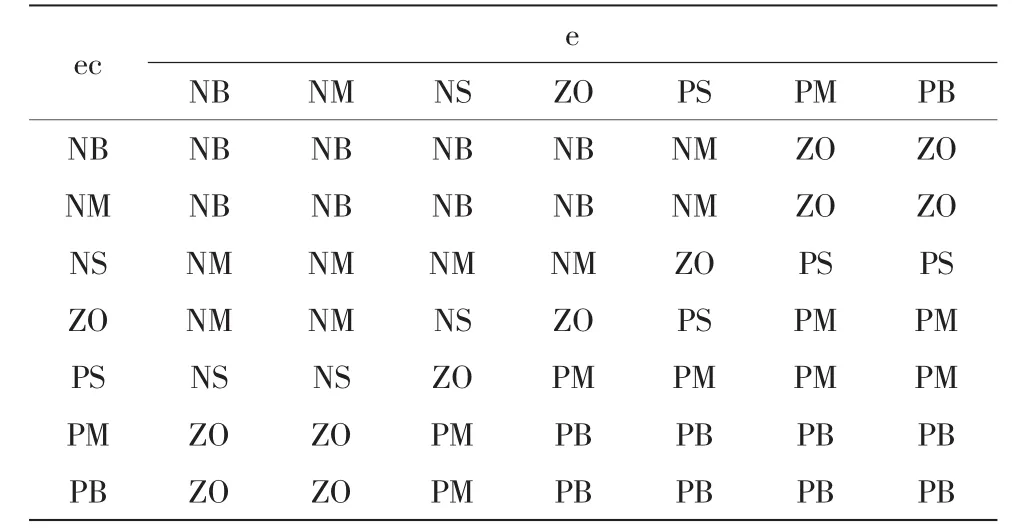
表2 PD型模糊控制规则表Tab.2 Table of PD fuzzy control rule

图6、图7、图8分别是PI型模糊控制器、PD型模糊控制器[8]、简化PID型模糊控制器的阶跃响应曲线。从图中可以看出，动态过程中，PI型模糊控制系统的响应超调大，而且过渡时间比较长，而简化PID型模糊控制系统不仅响应超调小，而且过渡时间也短。所以，PID型模糊控制系统的动态性能优于PI型模糊控制系统。在稳态过程中，PD型模糊控制系统引起的误差较大，而PID模糊控制系统可以消除稳态误差，这表明简化PID型模糊控制系统的稳态性能优于PD型模糊控制系统。

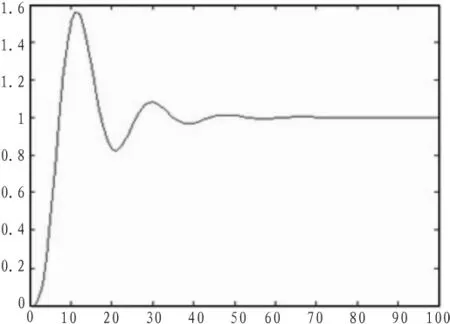
图6 PI型模糊控制系统的阶跃响应曲线Fig.6 Step response curve of PIfuzzy control system

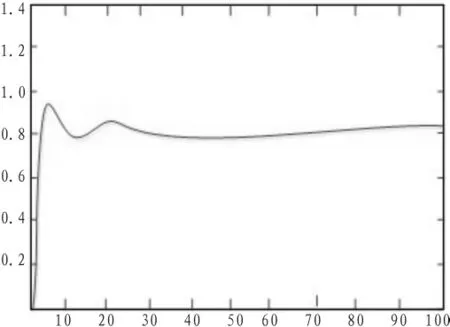
图7 PD型模糊控制系统的阶跃响应曲线Fig.7 Step response curve of PD fuzzy control system

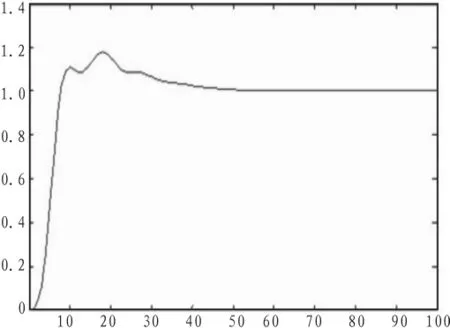
图8 PID型模糊控制系统的模糊曲线Fig.8 Step response curve of PID fuzzy control system

4 结 论

由上述仿真曲线可以表明，在各项控制器参数相同的情况下，简化PID型模糊控制系统的动态性能优于PI型模糊控制系统，稳态性方面优于PD型控制系统。而且相比较常规PID模糊控制器，它是二维输入，且只需建立一个控制规则数，大大的减小了工作的复杂度。

[1]刘定邦.大型风力发电机组的模糊控制研究[D].重庆：重庆大学，2007.

[2]程 静.智能控制在风力发电机控制系统中应用的研究[D].乌鲁木齐：新疆大学，2004.

[3]包献文，王维庆.模糊控制在风力发电系统功率控制中的应用[J].能源与环境，2009（5）:19－20，22.BAO Xian-wen，WANG Wei-qing.The application of fuzzy control in wind power generation system control[J].Energy and Environment，2009（5）:19－20，22.

[4]胡一倩.二维PID型模糊控制器在电厂过热汽温控制中的应用研究[D].南京:东南大学，2002.

[5]薛艳.电脑鼠模糊PID控制算法研究[D].西安:长安大学，2010.

[6]王正斐.电力系统故障限流器的研究[D].哈尔滨，哈尔滨工程大学，2008.

[7]王亮，王文策，程斌，等.基于Simulink的发电机励磁系统整流单元的建模与仿真[J].陕西电力，2011（7）：25－28.WANG Liang，WANG Wen-ce，CHENG Bin，et al.Modeling&simulation of generator excitation systemrectifier unit based on Simulink[J].Shaanxi Electric Power，2011（7）：25－28.

[8]王江荣，刘伟.基于Haar小波的一类模糊控制器的优化及应用[J].工业仪表与自动化装置，2011（5）：30－32.WANGJiang-rong，LIUWei.Haar wavelet-based fuzzycontroller for a class of optimization and application[J].Industrial Instrumentation&Automation，2011（5）：30－32.