多角度审视过山车问题——以运动学物理量解决动力学问题初探

麻志洪 陈亚琳

(浙江师范大学数理与信息工程学院 浙江 金华 321004)

1 过山车运动问题

日常生活中，我们经常有看到游乐园里的过山车从轨道上进行360°的大旋转，极为惊险刺激.但是，如果仔细思考，我们可以抽象出这样一个问题.

在忽略空气阻力条件下，过山车在轨道的上半部分某一点处速度至少达到多少时，过山车不会从该点掉下？

现将物理现象抽象为物理问题.如图1所示，位于竖直平面内的光滑圆形轨道，半径为R，一质量为m的小球在圆形轨道上运动，若小球能够通过图中P(x0,y0)位置不掉下(忽略一切阻力)，设此时小球的速度为v，问v至少为多少？

图1

2 多种解法

(1)运用牛顿运动定律求解

设此时轨道对小球的压力为N，小球与坐标轴原点的连线与y轴的夹角为θ.则

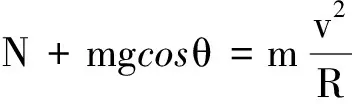
其中，N=0为临界状态.

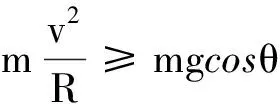
解得

创新点：运用牛顿运动定律形式简单，运算简便，具有相当大的优越性，同时也是学生常用的解法.

(2)运用矢量的方法求解

如图2，假设P点以上轨道不存在，小球将做斜抛运动，根据斜坐标法，斜抛运动可以等效成竖直方向的自由落体运动与沿着v方向的匀速直线运动.

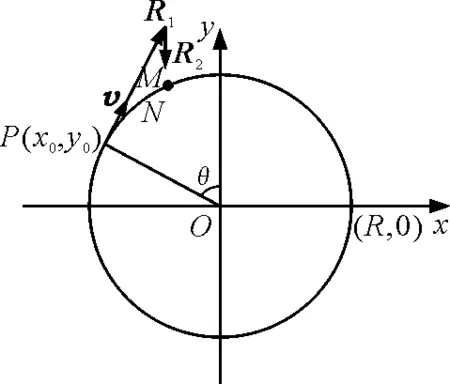
图2

设小球在P点开始做斜抛运动，经过很小的一段时间t(t→0)，则小球沿着v方向的位移矢量大小为R1，同时自由落体的位移矢量大小为R2，R1在竖直方向上的投影为R1cosθ，可得表达式

M(y)=R1sinθ-R2+Rcosθ

同时，与M横坐标相同的N点纵坐标为

要使小球不从轨道上掉下，只需要

M(y)≥N(y)

即得到表达式

(1)

将式(1)展开并化简可得

因为t→0，所以，令

要使该函数在t→0时大于零，则根据函数极限知识，解得

创新点：通过矢量的观点解决该问题，虽然运算上稍加复杂，却从一定程度上提示我们，这一问题是有其他解法的.

(3)对解法2的另一种阐述

我们可以通过解出使小球不能在轨道上的运动时的速度来解出答案.当小球不能在轨道上运动时，小球将做斜抛运动.

将速度v分解成水平方向vx与竖直方向vy.只需小球在很小一段时间内竖直方向上的上升高度小于因小球水平方向移动时圆上增加的高度，小球将不能沿着圆轨道运动.

只需要ΔH1≤ΔH2，即可解出小球不能沿轨道运动的速度.

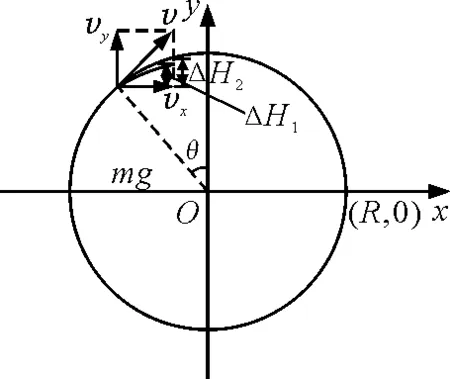
图3

后面的解法与解法2相同，再取v的在正实数的补集即解出答案，在此不做阐述.

创新点：此解法虽与解法2大体相同，但采用不同的速度分解方式亦体现出物理学不同的思考方式就有不同的物理解释.

(4)当小球位于P点时，P点在轨迹A上的右导数小于在轨迹B(即圆轨道上)上的右导数，由微分知识可知，存在区间(x1,x2)曲线A将位于曲线B下方，即小球将会脱离圆轨道.

图4

当时间取极限t→0时，P点在轨迹A上的右导数与离P点无限接近的轨迹A上的F点的切线斜率相等，同理，在轨迹B上的右导数与离P点无限接近的轨迹B上的M点的切线斜率相等，又已知轨迹A的切线方向即小球的速度方向，则当小球在P点刚好沿着A轨道运动时，在很小一段时间Δt后，速度倾斜角将小于对应相同横坐标圆上点的切线倾斜角.设v的倾斜角为α，t时间后切线的倾斜角为β，设圆的方程为x2+y2=R2，在P点对应的圆的方程为

可列出表达式

(2)

(3)

由极限知识可知，当小球不能沿着轨道运动时只需

tanα≤tanβ

将式(3)、(4)代入，因为t→0，略去高阶无穷小，可得

-2Rv3tsinθcos3θ<

2Rv3tsin3θcosθ-2vgtsinθcos2θR2

进一步化简并取v正实数上的补集即得出答案

创新点：通过做向心运动后速度倾斜角与圆切线倾斜角的关系得出答案也不失为一种方法.

(5)通过运动学方法，运用曲率知识进行求解.

数学知识补充：

其中，k为曲率半径，有

通过上述数学知识，可寻求y=y(x)的关系式，将物理问题转化为数学问题.

图5

假设P点以上轨道不存在，则小球在P点以后将有3种情况：

1)沿着路径c小球将会下落，不能沿着轨道运动；

2)沿着圆弧路径b，小球刚好能沿着轨道运动；

3)沿着路径a运动，则小球将会飞出轨道，此时也就是小球在P点的曲率半径大于圆的半径，列出小球的运动方程则有

x-x0=vtcosθ

联立得

所以

得

创新点：运用运动学知识结合曲率公式，也较为巧妙地解决动力学问题.

解法总结：从以上5种方法我们可以发现很有意思的一个物理现象，方法1利用加速度解题，方法2利用位移解题，而方法3利用速度解题，这几个物理量也正是运动学中最关键的物理量，均可作为解题思路，由此可见物理学体系的统一性.

3 多解过山车问题的思考

在物理的学习中，思维处于核心地位，而本节“一题多解“方法在一定程度上体现创新理念，注重各物理量既有联系又有差别的理念建立过程，注重科学的研究方法，应用全方位知识解决实际问题。

从创新思维的可行性入手，为问题的深入理解提供可靠的条件．在总体上，注意紧紧围绕学习目的，循序渐进地从提出问题，建立模型、全方位寻找方法去解释一些物理现象，以增强自身理性知识为突破口，走出思维定势的阴影，奔向创新的阳关大道.

参考文献

1 程君妮.开放实验与学生创新思维培养模式之初探.物理通报，2011(2)

2 陈礼，关伟.过山车动力学建模与仿真.中国工程机械学报，2010(4)

3 赵坚.机械能守恒定律理解中一个值得重视的问题.物理通报，2006(6)