两个平面镜成像的规律

余念祖

(昆明第十二中学 云南 昆明 650041)

对两个有一定夹角的平面镜成像问题的研究，是单个平面镜成像知识的扩展和延伸．两个平面镜成像的现象存在于我们生活中，只要我们稍加留意就不难发现它．因此，研究这一现象，发现它的规律也具有实际意义．

先对成像过程及相关名称作简单介绍．

如图1所示，设M，N两平面镜镜面夹角为θ

(0<θ<180°)，两镜面被纸面所截，且均垂直于纸面．AA′和BB′是两镜及其延展面跟纸面的交线，O点是这两直线的交点(也是三面交点)．今在两镜面间的纸面上任一位置放一个小物体S(可视为一个点)，线段SO跟M镜面的夹角∠SOA=α，跟N镜面的夹角∠SOB=β(平面镜两个面，一个是不反光的镜背，另一个是反光的镜面．这里的角是SO跟镜面的夹角).

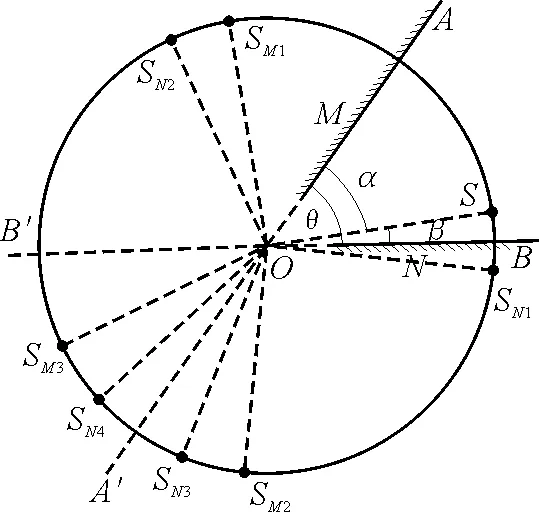
图1

S在M镜后对称位置成一像SM1．此像在N镜前，对N镜可作为物点而在其后成像SM2．SM2在M镜前，又可作为物而在M镜后成像SM3．直至一镜所成的像落在另一镜后或镜面上，这个像再也不能作为物而成像了．这个像是最后的像，叫做终像．图中SM3就是终像．为方便讨论，我们把S在M镜后的第一个像和以它为物反复在两镜后所成的像称为M系列的像，并按成像先后依次记为SM1，SM2，SM3，…，SMm．SMm便是M系列的终像．同理，我们把S在N镜后成的第一个像和以它为物反复在两镜后所成的像叫N系列的像(过程不再重复)．按先后依次记为SN1，SN2，SN3，…，SNn．SNn便是N系列的终像(图中N系列的终像是SN4)．像记号右下脚码第一个是字母，表示系列名称；第二个脚码是数字，表示它是该系列的第几个像．显然，第二脚码是奇数的像是跟该系列名称相同的镜(同名镜)所成的像，第二脚码为偶数的是跟该系列名称不相同的镜(异名镜)所成的像．如图中SM1，SM3，SN2，SN4是M镜成的像，SM2，SN1，SN3是N镜成的像．

物点和像点跟三面交点O的连线分别叫物心线和像心线(如SO、SM1O等)，其长度是物心距和像心距．物心线跟某镜面的夹角简称为物对该镜面的角；同样，某像心线跟某镜面的夹角称为该像对该镜面的角．这里须注意：物对同一镜的“面”和“背”之角的和是360°；同一像对同一镜的“面”和“背”之角的和也是360°．因此S对M镜面的角是α，则S对M镜背的角是360°-α．

下面我们就利用上述的说明和介绍讨论两平面镜成像的规律．

1 像和物共面共圆

先证明像和物共面．因物点在纸面上，纸面同时垂直两平面镜，而像和物又关于镜面对称，因此物点和它在两镜后反复所成的全部像都在纸面上．即像和物同在过物点而垂直于两镜的平面．

既然像和物共面，且又关于镜面对称，则所有的像心距必等于物心距．因此像和物都在以三面交点O为圆心，以物心距长为半径的圆周上．

2 两系列虚像数

系列中第几个像是终像，该系列就有几个像．但确定终像，须讨论终像区和终像条件．

2.1 终像区和终像条件．

我们知道，一镜所成之像位置在另一镜前，它可以作为物体在另一镜后成像．但如果一镜所成之像落在另一镜之后，它不能作为物而再次成像了．因此，不论哪一系列，也不论哪个平面镜所成的像，只要它落在以两镜延展面为边界所夹的区域内或边界上(图中OA′及OB′所夹之区域)，此像就再也不能作为物而成像了，这个像就是该系列的终像．上述的角∠A′OB′所占有的区域(含边界)叫终像区．

什么样的像才能落在终像区呢？从图中不难看出，当一镜所成的像对另一镜面之角等于或大于180°而又小于180°+θ时，此像一定在终像区了(等于180°时，像在边界上；大于180°而小于180°+θ时，像在终像区内)．因此终像条件应是：一镜所成的像对另一镜面的角等于或大于180°而小于180°+θ．

2.2 两系列各自的虚像数

从本文附图中可以看出在M系中：

S对M镜面的角φMO=α，在M镜后对称位置成像SM1；

SM1对N镜面的角φM1=θ+α<180°，表明SM1在N镜前，可作为物在N镜后成像SM2；

SM2对M镜面的角φM2=2θ+α<180°，表明SM2在M镜前还可作为物在M镜后成像SM3；

SM3对N镜面的角φM3=3θ+α>180°而小于180°+θ，表明SM3已在终像区内了．它是M系列的终像．M系列有3个像．

同理，在N系列中：

S对N镜面的角φNO=β，在N镜后成像SN1；

SN1对M镜面的角φN1=θ+β<180°，表明可作为物在M镜后成像SN2；

SN2对N镜面的角φN2=2θ+β<180°，表明可作为物在N镜后成像SN3；

SN3对M镜面的角φN3=3θ+β<180°，表明可作为物在M镜后成像SN4；

SN4对N镜面的角φN4=4θ+β>180°，但小于180°+θ，表明SN4在终像区内，SN4是系列的终像．N系列有4个像．

应注意上面讨论中两点：

(1)像记号和角记号的第二脚码就是θ角的系数．

(2)第二脚码若为奇数，该角是同名镜成的像对异名镜面的角；若为偶数，则该角是异名镜成的像对同名镜面的角．

现将上面的讨论推广到一般情况中去．

对M系列，若φMm=180°表示SMm在终像区边界上；若φMm>180°而小于180°+θ，则SMm在终像区内．表示SMm是M系列的终像．

对N系列，若φNn=180°在终像区边界上，若180°<φNn<180°+θ，表示SNn在终像区区域内．SNn是N系列的终像．

因此，如果SMm和SNn是终像则一定有

180°≤φMm<180°+θ

180°≤φNn<180°+θ

因φMm=mθ+α，φNn=nθ+β，故有

180°≤mθ+α<180°+θ

(1)

180°≤nθ+β<180°+θ

(2)

此两式就是终像条件式．

由此可知M系列有m个像，N系列有n个像，但m和n的数值还需进一步讨论．由式(1)、(2)可知m和n应满足

和

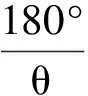
180°=kθ+δ

代入(1)、(2)两式后整理得

(3)

(4)

上两式中m和n只能是自然数，因此当

(5)

(6)

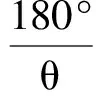
3 虚像的总数

两平面镜所成虚像的总数不一定等于m+n因两系列的终像可能重合．如果重合，则总像数

Z=m+n-1

重合条件的讨论并不十分困难，因所有的像是共面共圆的，只要讨论终像对相应镜面的角就足够了．下面分两种情况讨论．

(1)若m≠n，它们的差仅为1，因此若一个是奇数，另一个必为偶数，那么φMm和φNn必为两终像SMm和SNn对同一个镜面的角．若要两终像重合必须φMm=φNn，即mθ+α=nθ+β．由于α和β均小于θ，它们的差更不可能等于θ，则等式φMm=φNn不成立．故当m≠n时，两终像不重合．

(2)若m=n，则m和n同为奇数或同为偶数，那么φMm和φNn必为两终像对不同镜面的角，故考虑到两镜面朝向相反(顺时针和逆时针方向)，且夹角为θ，要使两终像重合，必须

φMm+φNn=360°+θ

如果m=n=k+1，左边

φMm+φNn=mθ+α+nθ+β=

(k+1)θ+α+(k+1)θ+β=2kθ+3θ

右边

360°+θ=2×180°+θ=

2(kθ+δ)+θ=2kθ+2δ+θ

因δ<θ，则φMm+φNn>360°+θ，两终像也不重合．

如果m=n=k，左边

φMn+φNn=mθ+a+nθ+β=

2kθ+(a+β) =2kθ+θ

右边

360°+θ=2kθ+2δ+θ

显然如果δ≠0，上述重合条件式φMm+φNn=360°+θ不能成立，两终像仍不重合．只有当δ=0时，φMm+φNn=360°+θ才能成立，两终像才重合．

因此两终像重合必要而充分的条件是：δ=0，

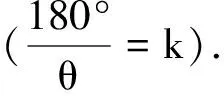
这样，虚像的总数就有以下几种可能.

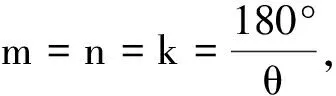
(2)δ≠0时，终像不重合，这时m和n可能同为k；可能一为k，一为k+1，也可能同为k+1．则虚像总数Z=2k或Z=2k+1或Z=2k+2．具体的数值要由式(5)至式(8)中的条件决定．

可见两平面镜成的像总数不仅决定于θ角，还决定于角α和β的大小(物点的位置)．

4 对以上所讨论的规律须注意几点

(1)上述公式是在0<θ<180°的情况下推出的．若θ=180°，上述公式无实际意义．因θ=180°时，实际就是一个平面镜，不可能有两系列的像．

(2)若θ=0，上述公式不再适用．但若θ=0看成是两平面镜镜面对镜面平行的话．那么上述的某些方法和结论仍然是有用的．例如，当两镜面不在一平面且相向平行，就没有终像区了，可成无限多个像；又因两镜面相向不在一平面且平行，则过镜面的两平面永不相交，这可以理解为物心距无限大，像心距也无限大，则可视为物点和它的全部像点均分布在同一直线上(共线)．

5 总结

以上的论述和证明较散，需要归纳一下．

5.1 符号和脚码

SMm和SNn，φNm，φNn分别为两系列的像符号和角符号．第一脚码是系列名称；第二脚码是数字．第二脚码若为奇数，则该像是同名镜所成之像；该角是该像对异名镜面所夹的角．第二脚码若为偶数，则该像是异名镜所成之像，该角是该像对同名镜面所夹的角．如SM3是M镜成的像，φM3是SM3对N镜面的夹角；SN2是M镜成的像，φN2是SN2对N镜面的夹角．

5.2 成像规律

(1)共面共圆．特珠情况下还共直线．

(2)成像数的确定

终像条件

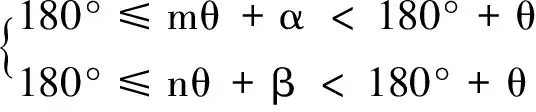
(7)

式中m，n应满足

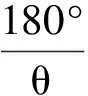
(8)

上两式中m和n只能是自然数，故当

(9)

(10)

已证明：δ=0时(即180°能被θ整除时)，两系列终像重合，故成像总数Z=m+n-1；其他情况Z=m+n，故考虑到式(9)、(10)中的条件，总像数Z=2k或Z=2k+1或Z=2k+2．

6 举例

【例1】设M和N两平面镜镜面夹角为θ，物点S对M，N镜面的角分别为α和β．试求

(1)θ=50°，α=40°，β=10°；

(2)θ=50°，α=26°，β=24°；

(3)θ=55°，α=30°，β=25°.

三种情况时像的总数．

解析

(1)当θ=50°，α=40°，β=10°时，k=3，δ=30°．由于余数δ不为零，两终像不重合，又因β<δ<α，根据式(5)和式(8)，得m=k=3．n=k+1=4，则总像数Z=m+n=7个；

(2)θ=50°，α=26°，β=24°时，k=3，δ=30°，两终像不重合，且δ既大于α又大于β，根据式(6)和式(8)，得m=n=k+1=4，则总像数Z=m+n=8个；

(3)θ=55°，α=30°，β=25°时，k=3，δ=15°，两终像不重合，且δ<α，又δ<β，根据式(5)和式(7)，得m=n=k=3，则总像数Z=m+n=6个．

【例2】两平面镜M，N的镜面夹角θ=60°，物点S对M，N镜面的角分别为α=40°，β=20°．求两镜所成虚像总数及终像位置．

解析：θ=60°，α=40°，β=20°时，k=3，δ=0两终像重合，且由式(5)和式(7)得m=n=k=3，则虚像总数Z=m+n-1=6-1=5个．

因φMm=φM3=3θ+α=3×60°+40°=220°，m=3为奇数，则φM3是终像SM3对异名镜(N镜)镜面的角．故两终像重合于对N镜面的角为220°以O点为圆心、以物心距长为半径的圆周上一点．

为减少篇幅，上述例子的图形省略了．请读者自行作图验证上例中的结果．